备战数学建模32-相关性分析2
目录
一、皮尔逊相关系数
二、斯皮尔曼相关系数
三、典型相关分析
1-定义及具体步骤
2-典型相关分析的案例1
3-典型相关分析的案例2
本节重点学习两种相关性分析,pearson和spearman,它们可以衡量两个变量之间相关性的大小,我们需要根据数据满足的不同条件,选择不同的相关系数进行计算和分析,具体介绍一些细节,个人感觉还是比较重要的,防止相关性分析的滥用。同时,我们也讨论了典型相关分析的应用,主要用于解决两组变量之间相关关系的一种多元线性统计方法。
一、皮尔逊相关系数
我们先看一下皮尔逊和斯皮尔曼的使用要求,对于皮尔逊要求变量是连续数据,且变量之间具有线性关系,且要求数据服从正态分布,而且一般皮尔逊要求用在定距和定距变量之间的相关性检验,定序与定序变量要求用斯皮尔曼。
由于皮尔逊相关性检验的限制比较多,所有我们在使用之前需要进行限制条件的验证,由于是否是定距变量及是否连续可以直接看出来,故我们首先需要对变量进行线性检验,通过SPSS绘制矩阵散点图,来判断变量之间是否具有线性关系,必须有线性关系,才能使用皮尔逊检验。
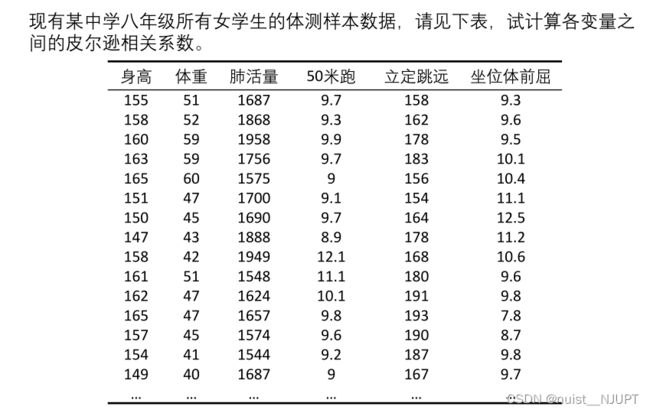
我们看一个例子就可以了,具体如下:
第一步:对于数据,我们最好首先进行描述性统计,这样是一个好习惯,就是计算出各项指标的最值,均值,标准差,偏度和峰度之类的,可以用SPSS或者MATLAB等实现,当然EXCEL也可以,哈哈哈哈。
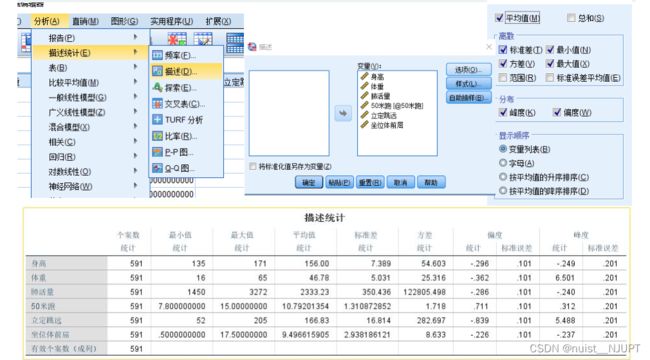
SPSS描述统计的方法简单,导入数据后,选择描述统计,将变量导入,就可以自动计算了,如下所示。
当然MATLAB编程实现也很简单,代码如下:
clear; clc
load('test_data.mat')
format short g
%描述性统计
Min = min(test) ;
Max = max(test) ;
Mean = mean(test) ;
Median = median(test) ;
Skewness = skewness(test) ; %偏度
Kurtosis = kurtosis(test) ; %峰度
Std = std(test) ;
Result = [Min; Max; Mean; Median; Skewness; Kurtosis; Std] ;
disp('描述统计如下所示:') ;
disp(Result) ;
第二步,就是使用SPSS绘制矩阵散点图了,具体的操作如下,选择图形->旧对话框->散点图->矩阵三散点图,绘制的矩阵散点图如下,当然,上述表格数据是随机生成的,正常建模多数都有线性关系的。
第三步,假设上述散点图各变量之间具有线性关系,下面我们就要计算皮尔逊相关系数,具体MATLAB程序如下,当然用SPSS也是可以计算的。
%计算皮尔逊相关系数
R = corrcoef(test) ;
disp('皮尔逊相关系数如下:') ;
%xlswrite('D:\r1.xlsx',R) ;
disp(R) ;
我们可以看一下SPSS进行皮尔逊相关性分析的结果,具体如下:
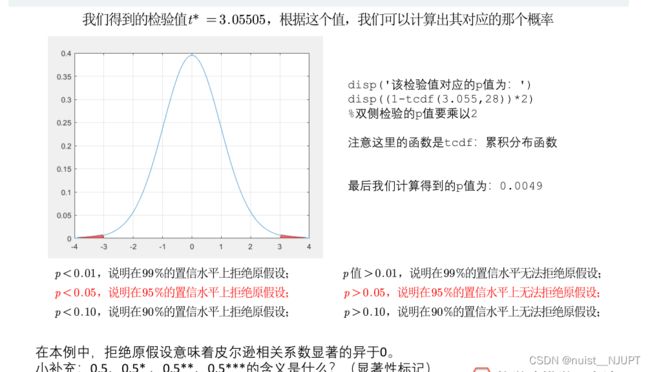
对于求出的皮尔逊相关系数进行假设检验,p值检验法,p值越小,相关性越靠近1,通过p值拒绝原假设,说明皮尔逊相关系数显著异于0.
第四步,需要进行正态分布检验,对于大样本数据,可以使用 JB检验和QQ图检验。对于小样本的数据,使用夏皮洛-威尔克检验。
JB检验的MATLAB代码如下,注意:这个原假设是正态分布,我们不能拒绝原假设才是说明服从正态分布。
%对于大样本数据,n>30的数据,正态分布检验,使用JB检验,即雅克-贝拉检验
[h,p] = jbtest(test(:,1),0.05) ; %检测第一列的数据是否为正态分布
%用循环检验所有列的数据
n_c = size(test, 2) ;
H = zeros(1,6) ;
P = zeros(1,6) ;
for i = 1 : n_c
[h,p] = jbtest(test(:,i), 0.05) ;
H(i) = h ;
P(i) = p ;
end
%如果H等于1表示拒绝原假设,P<0.5可以拒绝原假设
disp('H值如下所示:') ;
disp(H) ;
disp('P值如下所示:') ;
disp(P) ;当然也可以使用 QQ图检测大样本是否服从在正态分布,不过这个只能看趋势,不够准确。
本题中绘制QQ图的代码如下:
subplot(2,3,1) ;
qqplot(test(:,1)) ;
title('身高数据与标准正态的QQ图') ;
xlabel('标准正态数') ;
ylabel('输入样例数') ;
subplot(2,3,2);
qqplot(test(:,2)) ;
title('体重数据与标准正态的QQ图') ;
xlabel('标准正态数') ;
ylabel('输入样例数') ;
subplot(2,3,3) ;
qqplot(test(:,3)) ;
title('肺活量数据与标准正态的QQ图') ;
xlabel('标准正态数') ;
ylabel('输入样例数') ;
subplot(2,3,4);
qqplot(test(:,4)) ;
title('50米跑数据与标准正态的QQ图') ;
xlabel('标准正态数') ;
ylabel('输入样例数') ;
subplot(2,3,5) ;
qqplot(test(:,5)) ;
title('立定跳远数据与标准正态的QQ图') ;
xlabel('标准正态数') ;
ylabel('输入样例数') ;
subplot(2,3,6);
qqplot(test(:,6)) ;
title('坐位体前屈数据与标准正态的QQ图') ;
xlabel('标准正态数') ;
ylabel('输入样例数') ;QQ图如下,要是近似于一条直线,则说明服从正态分布,具体如下:
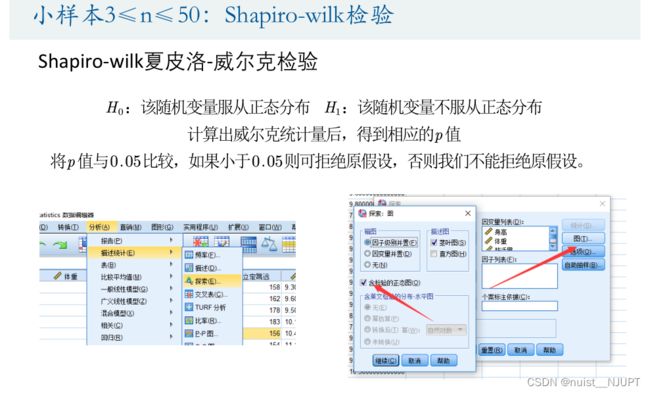
对于小样本的数据使用夏皮洛-威尔克检验是否服从正态分布,SPSS实现步骤,具体如下:
检验结果如下,如果显著性小于0.05,则拒绝原假设,则说明不服从正态分布。
皮尔逊检验,完整的MATLAB代码如下:
clear; clc
load('test_data.mat')
format short g
%描述性统计
Min = min(test) ;
Max = max(test) ;
Mean = mean(test) ;
Median = median(test) ;
Skewness = skewness(test) ; %偏度
Kurtosis = kurtosis(test) ; %峰度
Std = std(test) ;
Result = [Min; Max; Mean; Median; Skewness; Kurtosis; Std] ;
disp('描述统计如下所示:') ;
disp(Result) ;
%在计算皮尔逊系数之前,需要做出散点图,根据散点图观察两组变量是否具有线性关系
%我们可以使用SPSS实现上述操作,在图形选项中操作
%对于大样本数据,n>30的数据,正态分布检验,使用JB检验,即雅克-贝拉检验
[h,p] = jbtest(test(:,1),0.05) ; %检测第一列的数据是否为正态分布
%用循环检验所有列的数据
n_c = size(test, 2) ;
H = zeros(1,6) ;
P = zeros(1,6) ;
for i = 1 : n_c
[h,p] = jbtest(test(:,i), 0.05) ;
H(i) = h ;
P(i) = p ;
end
%如果H等于1表示拒绝原假设,P<0.5可以拒绝原假设
disp('H值如下所示:') ;
disp(H) ;
disp('P值如下所示:') ;
disp(P) ;
%对于小样本的数据可以使用夏皮洛‐威尔克检验是否是正态分布
%可以用SPSS实现
%当然还有一种检验是否是正态分布的方式Q-Q图,当然该方式要求数据量比较大才行,而且只是能看趋势
subplot(2,3,1) ;
qqplot(test(:,1)) ;
title('身高数据与标准正态的QQ图') ;
xlabel('标准正态数') ;
ylabel('输入样例数') ;
subplot(2,3,2);
qqplot(test(:,2)) ;
title('体重数据与标准正态的QQ图') ;
xlabel('标准正态数') ;
ylabel('输入样例数') ;
subplot(2,3,3) ;
qqplot(test(:,3)) ;
title('肺活量数据与标准正态的QQ图') ;
xlabel('标准正态数') ;
ylabel('输入样例数') ;
subplot(2,3,4);
qqplot(test(:,4)) ;
title('50米跑数据与标准正态的QQ图') ;
xlabel('标准正态数') ;
ylabel('输入样例数') ;
subplot(2,3,5) ;
qqplot(test(:,5)) ;
title('立定跳远数据与标准正态的QQ图') ;
xlabel('标准正态数') ;
ylabel('输入样例数') ;
subplot(2,3,6);
qqplot(test(:,6)) ;
title('坐位体前屈数据与标准正态的QQ图') ;
xlabel('标准正态数') ;
ylabel('输入样例数') ;
%计算皮尔逊相关系数
R = corrcoef(test) ;
disp('皮尔逊相关系数如下:') ;
%xlswrite('D:\r1.xlsx',R) ;
disp(R) ;
二、斯皮尔曼相关系数
我们再看一下这个对比,当我们发现不难使用皮尔逊相关系数检验,则我们可以考虑使用 斯皮尔曼检验,具体如下:
使用MATLAB和SPSS可以求斯皮尔曼相关系数,本次给出MATLAB代码,SPSS操作看我另一篇相关性分析的博客。
clear; clc
load('test_data.mat')
format short g
%计算斯皮尔曼相关系数
R = corr(test, 'type', 'Spearman') ;
disp('斯皮尔曼相关系数如下:') ;
disp(R) ;对于斯皮尔曼的假设检验,p值小于0.05,则可以拒绝原假设,则说明和0有显著性差异,否则不难拒绝原假设。
三、典型相关分析
1-定义及具体步骤
一般的相关性分析用于分析两个变量之间的相关性,如果我们需要考虑两组变量之间的相关性,则需要使用典型相关分析。
我们可以先看一下典型相关分析的思路,其实类似于降维,就是将多个变量的进行线性组合成,形成一个综合变量,求解综合变量之间的相关性。
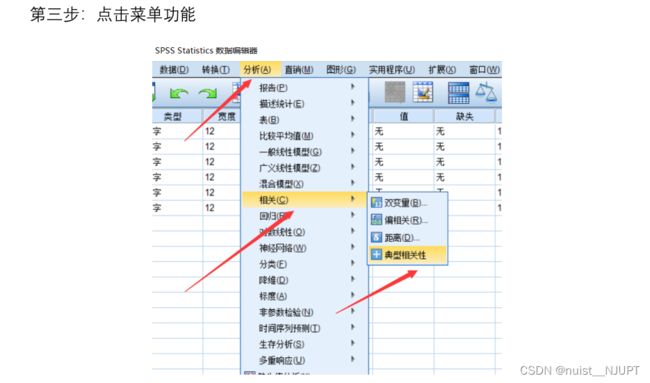
我们使用SPSS进行典型相关分析,需要使用SPSS24版本以上,具体如下,首先导入数据:
然后数据检验,正常的数据都是标度,如下所示。
然后进行典型相关分析即可,分别导入两组变量,如下:
接下来,将分析的数据结果到处到你想要的位置即可。
2-典型相关分析的案例1
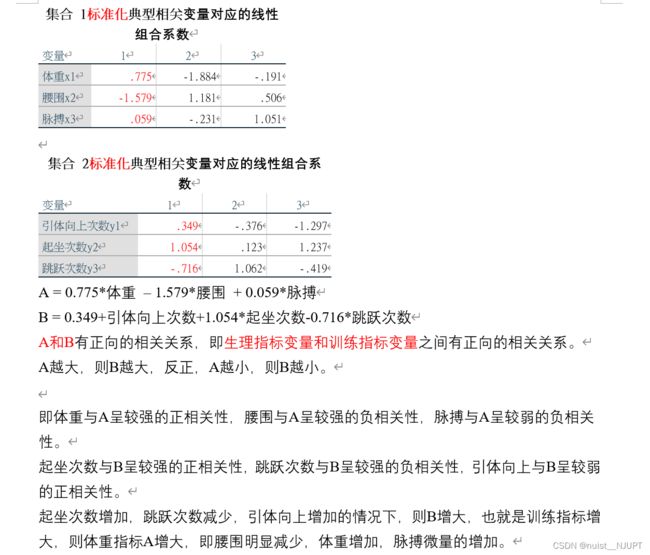
对下面身体指标数据进行典型相关分析,具体步骤参照上面的就可以。
我的分析的结果如下所示:
3-典型相关分析的案例2
我们要探究观众和业内人士对于一些电视节目的观点有什么样的关系呢?
观众评分来自低学历(led)、高学历(hed)和网络(net)调查三种,它们形成第一组变量;
而业内人士分评分来自包括演员和导演在内的艺术家(arti)、发行(com)与业内各
部门主管(man)三种,形成第二组变量。按照上述典型相关分析步骤,我的分析结果如下: