二叉树经典例题
前言:
本文主要讲解了关于二叉树的简单经典的例题。
因为二叉树的特性,所以关于二叉树的大部分题目,需要利用分治的思想去递归解决问题。
分治思想:
把大问题化简成小问题(根节点、左子树、右子树),返回条件就是最小规模的子问题!
一、二叉树中结点的个数
思路:
采用分而治之的思想, 先访问左子树,再访问右子树,然后再加上自己的个数也就是1。
原码:
//采用分治的思想去解决
int TreeSize(BTNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
/*if (root == NULL)
return 0;
else
{
return TreeSize(root->left) + TreeSize(root->right) + 1;
}*/
}二、二叉树中叶子结点的个数
思路:
分为三个判断条件。
- 如果是空结点,就返回0
- 如果是叶子结点就返回1
- 不满足上述两种情况,就继续访问左子树+右子树
原码:
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}三、求第k层的结点个数
思路:
当前树的第k层 = 左子树的k-1层 + 右子树的k-1层,以此类推
当k == 1时,如果不为空结点,就返回1,如果是空结点就返回0。
原码:
int TreeKLevel(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
return 0;
if (k == 1)
{
return 1;
}
return TreeKLevel(root->left, k - 1)
+ TreeKLevel(root->right, k - 1);
}四、判断单值二叉树
965. 单值二叉树
思路:
首先明确等号具有传递性,只要根节点和右节点相等,然后根节点与左结点相等,就说明这颗小树就是单值。
并且这是前序遍历,先遍历根节点,如果根节点不是单值二叉树,那么就没有必要去遍历后面的。
这点可以利用&&与操作符实现,与操作符的特性是只要前者是假,后面就不会执行
原码:
bool isUnivalTree(struct TreeNode* root){
//采用前序的思想
//利用等于号的传递性
if(root == NULL)
return true;
//跟左节点比较
if(root->left)
{
if(root->val != root->left->val)
return false;
}
//跟右结点比较
if(root->right)
{
if(root->val != root->right->val)
return false;
}
return isUnivalTree(root->left) && isUnivalTree(root->right);
}五、销毁二叉树
思路:
采用后序遍历,防止先销毁根节点,导致左右节点找不到了
原码:
void DestroryTree(BTNode* root)
{
//递归必须要有判断条件
if (root == NULL)
return;
//需要后序遍历,不然先销毁根节点,左右子树就找不到了
DestroryTree(root->left);
DestroryTree(root->right);
free(root);
root = NULL;六、在二叉树中根据值搜索结点
思路:
可以直接采取前序遍历,
- 最小子问题就是当结点为空时返回空
- 结点的值就是寻找的值就返回该节点
- 不满足上述条件,就继续递归遍历,先左子树再右子树,如果左子树已经找到结点,直接返回
原码:
BTNode* TreeFind(BTNode* root, int x)
{
if (root == NULL)
return NULL;
if (root->val == x)
return root;
BTNode* ret = TreeFind(root->left, x);
if (ret != NULL)
return ret;
return TreeFind(root->right, x);
}七、检查两颗树是否相同
100. 相同的树
思路:
采用分治的思想,把问题逐步缩小,最小子问题就是两个结点是否相同
- 我们首先要清楚是不是空树
- 然后如果一个为空,另一个不为空
- 当结点都存在时,再判断结点的值是否相等
原码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//分治子问题变成一个结点一个结点的比较
//如果两个都为空
if(p == NULL && q == NULL)
return true;
//如果有一个为空
if(p == NULL || q == NULL)
return false;
//如果两个都不为空
if(p->val != q->val)
return false;
return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}八、对称二叉树
101. 对称二叉树
思路;
本题跟上一题两颗二叉树是否相同非常相似,只需要将比较的结点改变顺序,因为是对称,所以左节点要跟右节点相等。
原码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//分治子问题变成一个结点一个结点的比较
//如果两个都为空
if(p == NULL && q == NULL)
return true;
//如果有一个为空
if(p == NULL || q == NULL)
return false;
//如果两个都不为空
if(p->val != q->val)
return false;
return isSameTree(p->left,q->right) && isSameTree(p->right,q->left);
}
bool isSymmetric(struct TreeNode* root){
return isSameTree(root->left,root->right);
}
九、另一棵树的子树
572. 另一棵树的子树
思路:
这道题也是判断相同树的衍生题目,当根节点与subTree的根节点相同时,可以判断两颗树是否相同,并利用||来判断。
原码:
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
//防止递归到空结点,造成非法访问
if(root == NULL)
return false;
//相同前提是根节点要一致
if(root->val == subRoot->val)
{
if(isSameTree(root,subRoot))
return true;
}
//只要发现相同,没有必要进行下面的比较,所以是||
return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
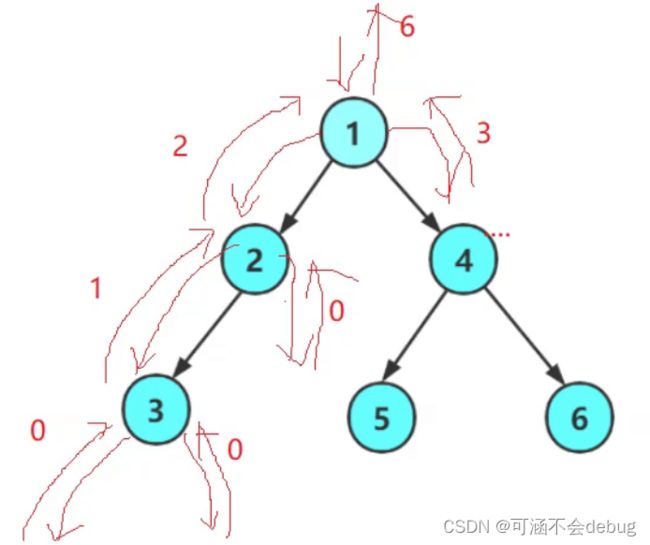
}十、二叉树的最大深度
104. 二叉树的最大深度
思路:
我们分别求出左子树和右子树的深度,再返回较大的值。
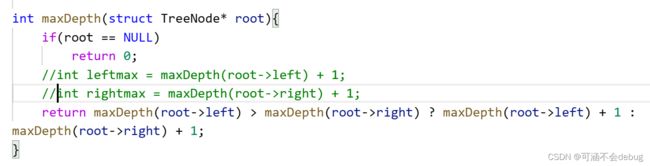
注意:
我们不能将代码写成上面的形式,首先定位上面的代码是非常差的代码,返回值返回的时候会重新进入函数计算,并且是每一个结点!因此我们需要提前将返回值保存起来,将值进行比较去返回。
原码:
int maxDepth(struct TreeNode* root){
if(root == NULL)
return 0;
int leftmax = maxDepth(root->left) + 1;
int rightmax = maxDepth(root->right) + 1;
return leftmax > rightmax ? leftmax : rightmax;
}十一、二叉树的前序遍历
144. 二叉树的前序遍历
思路:
本题并不是简单的递归求解,需要根据题目要求,因为我们用C语言进行求解。
- 数组的大小需要我们先自己求这颗树的结点大小,单独开辟一个函数去求解
- 我们不能递归自己的函数,因为每次递归都需要动态开辟一个新的数组,因此还需要重新创建一个函数去解决
- 注意新的函数中数组下标i的值需要传地址,因为递归过程中有很多i,直接传地址
原码:
//先提前算好二叉树结点的个数,便于开辟动态数组的大小
int TreeSize(struct TreeNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
void preorder(struct TreeNode* root,int* arr,int* i)//传数组下标的地址,避免使用全局变量的麻烦
{
if(root == NULL)
{
return;
}
arr[(*i)] = root->val;
(*i)++;
preorder(root->left,arr,i);
preorder(root->right,arr,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
*returnSize = TreeSize(root);
int *arr = (int*)malloc(sizeof(int)*(*returnSize));
//需要再创建一个函数用来递归,不然每次调用该函数进行递归都会动态开辟
int i = 0;
preorder(root,arr,&i);
return arr;
}十二、通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
注意:
*pi++ (*pi)++两者含义不同,为了避免优先级的问题,我们直接加上括号!
原码:
BTNode* BinaryTreeCreate(char* str, int* pi)
{
if (str[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode) * 1);
root->val = str[*pi];
(*pi)++;
root->left = BinaryTreeCreate(str, pi);
root->right = BinaryTreeCreate(str, pi);
return root;
}十三、二叉树的层序遍历
涉及到层序遍历,大部分情况下需要借助队列进行求解。
思路:
上一层带下一层,先进先出。
原码:
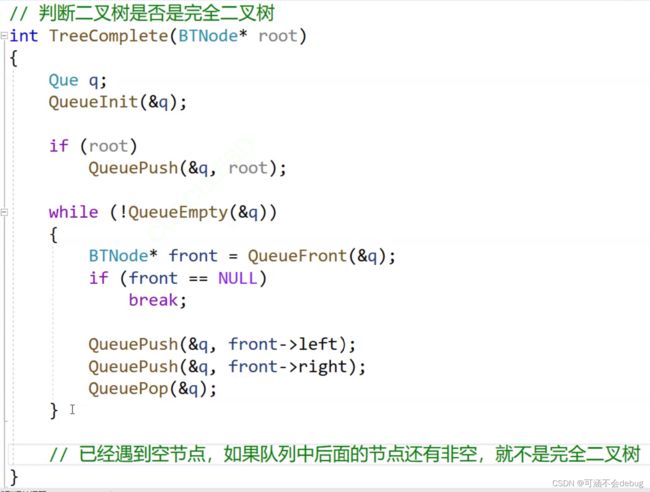
十四、判断是否是完全二叉树
思路:
利用层序遍历,如果非空结点是连续的,就是完全二叉树。
如果非空结点是不连续的,中间有空结点,就是非完全二叉树。