第一课数组、链表、栈、队列
第一课数组、链表、栈、队列
-
- acwing136 邻值查找---中等
-
- 题目描述
- 代码展示
- lc20.有效的括号--简单
-
- 题目描述
- 代码展示
- lc25.K 个一组翻转链表--困难
-
- 题目描述
- 代码展示
- lc26.删除有序数组中的重复项--简单
-
- 题目描述
- 代码展示
- lc88.合并两个有序数组--简单
-
- 题目描述
- 代码展示
- lc141.环形链表--简单
-
- 题目描述
- 代码展示
- lc142.环形链表II--中等
-
- 题目描述
- 代码展示
- lc150.逆波兰表达式求值--中等
-
- 题目描述
- 代码展示
- 155.最小栈--中等
-
- 题目描述
- 代码展示
- lc206.翻转链表--简单
-
- 题目描述
- 代码展示
- lc227.基本计算器II--中等
-
- 题目描述
- 代码展示
- lc224.基本计算器--困难
-
- 题目描述
- 代码展示
- lc283.移动零--简单
-
- 题目描述
- 代码展示
- lc641.设计循环双端队列--中等
-
- 题目描述
- 代码展示
acwing136 邻值查找—中等
题目描述
代码展示
// 邻值查找
#includelc20.有效的括号–简单
题目描述
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = "()"
输出:true
示例 2:
输入:s = "()[]{}"
输出:true
示例 3:
输入:s = "(]"
输出:false
提示:
1 <= s.length <= 104s仅由括号'()[]{}'组成
代码展示
C++:
class Solution {
public:
bool isValid(string s) {
std::stack<char> st;
for (char ch : s) {
if (ch == '(') st.push(')');
else if (ch == '[') st.push(']');
else if (ch == '{') st.push('}');
else if (!st.empty() && ch == st.top()) st.pop();
else return false;
}
return st.empty();
}
};
python:
class Solution:
def isValid(self, s: str) -> bool:
stack = list([])
for ch in s:
if ch == '(' or ch == '[' or ch == '{':
stack.append(ch)
else:
if len(stack) == 0:
return False
if ch == ')':
if stack[len(stack) - 1] != '(':
return False
elif ch == ']':
if stack[len(stack) - 1] != '[':
return False
else:
if stack[len(stack) - 1] != '{':
return False
stack.pop()
return len(stack) == 0
lc25.K 个一组翻转链表–困难
题目描述
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
示例 1:
输入:head = [1,2,3,4,5], k = 2
输出:[2,1,4,3,5]
示例 2:
输入:head = [1,2,3,4,5], k = 3
输出:[3,2,1,4,5]
提示:
- 链表中的节点数目为
n 1 <= k <= n <= 50000 <= Node.val <= 1000
代码展示
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
ListNode protect = new ListNode(0, head);
// 分组(找到每一组的开始、结尾),按组遍历
// last = 上一组结尾
ListNode last = protect;
while (head != null) {
ListNode end = getEnd(head, k);
if (end == null) {
break;
}
ListNode nextGroupHead = end.next;
// 处理head到end之间的k-1条边的反转
reverseList(head, end);
// 上一组跟本组的新开始(旧end)建立联系
last.next = end;
// 本组的新结尾(head)跟下一组建立联系
head.next = nextGroupHead;
// 分组遍历
last = head;
head = nextGroupHead;
}
return protect.next;
}
private ListNode getEnd(ListNode head, int k) {
while (head != null) {
k--;
if (k == 0) break;
head = head.next;
}
return head;
}
// head到end之间反过来
private void reverseList(ListNode head, ListNode end) {
if (head == end) return;
ListNode last = head;
head = head.next;
// 改每条边,所以需要访问链表
while (head != end) {
ListNode nextHead = head.next;
// 改一条边
head.next = last;
// last,head向后移动一位
last = head;
head = nextHead;
}
end.next = last;
}
}
lc26.删除有序数组中的重复项–简单
题目描述
给你一个 非严格递增排列 的数组 nums ,请你** 原地** 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
- 更改数组
nums,使nums的前k个元素包含唯一元素,并按照它们最初在nums中出现的顺序排列。nums的其余元素与nums的大小不重要。 - 返回
k。
判题标准:
系统会用下面的代码来测试你的题解:
int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案
int k = removeDuplicates(nums); // 调用
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums[i] == expectedNums[i];
}
如果所有断言都通过,那么您的题解将被 通过。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示:
1 <= nums.length <= 3 * 104-104 <= nums[i] <= 104nums已按 非严格递增 排列
代码展示
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int n = 0;
// 主题思路:保留与上一个不一样的
// 细节判断:i-1不能越界,第0个肯定要
for (int i = 0; i < nums.size(); i++) {
if (i == 0 || nums[i] != nums[i - 1]) {
nums[n] = nums[i];
n++;
}
}
return n;
}
};
lc88.合并两个有序数组–简单
题目描述
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
**注意:**最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[j] <= 109
代码展示
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int i = m - 1, j = n - 1;
// 主题思路:ij两个指针倒着扫描,谁大要谁
// 细节判断:i,j不能越界(一个<0,就要另一个)
for (int k = m + n - 1; k >= 0; k--) {
if (j < 0 || (i >= 0 && nums1[i] >= nums2[j])) {
nums1[k] = nums1[i];
i--;
} else {
nums1[k] = nums2[j];
j--;
}
}
}
};
lc141.环形链表–简单
题目描述
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:
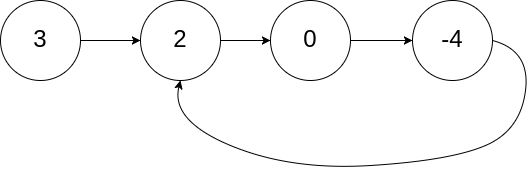
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:false
解释:链表中没有环。
提示:
- 链表中节点的数目范围是
[0, 104] -105 <= Node.val <= 105pos为-1或者链表中的一个 有效索引 。
代码展示
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode *head) {
ListNode* fast = head;
while (fast != nullptr && fast->next != nullptr) {
fast = fast->next->next;
head = head->next;
if (fast == head) return true;
}
return false;
}
};
lc142.环形链表II–中等
题目描述
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
- 链表中节点的数目范围在范围
[0, 104]内 -105 <= Node.val <= 105pos的值为-1或者链表中的一个有效索引
代码展示
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
while (fast != nullptr && fast->next != nullptr) {
fast = fast->next->next;
slow = slow->next;
if (fast == slow) {
while (head != slow) {
head = head->next;
slow = slow->next;
}
return head;
}
}
return nullptr;
}
};
lc150.逆波兰表达式求值–中等
题目描述
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。 - 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
示例 1:
输入:tokens = ["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出:22
解释:该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
提示:
1 <= tokens.length <= 104tokens[i]是一个算符("+"、"-"、"*"或"/"),或是在范围[-200, 200]内的一个整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如
( 1 + 2 ) * ( 3 + 4 )。 - 该算式的逆波兰表达式写法为
( ( 1 2 + ) ( 3 4 + ) * )。
逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成
1 2 + 3 4 + *也可以依据次序计算出正确结果。 - 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
代码展示
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<long long> s;
for (string& token : tokens) {
// 是运算符,取出栈顶两个操作数,运算结果入栈
if (token == "+" || token == "-" || token == "*" || token == "/") {
long long b = s.top();
s.pop();
long long a = s.top();
s.pop();
s.push(calc(a, b, token));
} else {
// 操作数入栈
s.push(stoi(token));
}
}
return s.top();
}
long long calc(long long a, long long b, string op) {
if (op == "+") return a + b;
if (op == "-") return a - b;
if (op == "*") return a * b;
if (op == "/") return a / b;
return 0;
}
};
155.最小栈–中等
题目描述
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack()初始化堆栈对象。void push(int val)将元素val推入堆栈。void pop()删除堆栈顶部的元素。int top()获取堆栈顶部的元素。int getMin()获取堆栈中的最小元素。
示例 1:
输入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
提示:
-231 <= val <= 231 - 1pop、top和getMin操作总是在 非空栈 上调用push,pop,top, andgetMin最多被调用3 * 104次
代码展示
class MinStack {
stack<int> x_stack;
stack<int> min_stack;
public:
MinStack() {
min_stack.push(INT_MAX);
}
void push(int x) {
x_stack.push(x);
min_stack.push(min(min_stack.top(), x));
}
void pop() {
x_stack.pop();
min_stack.pop();
}
int top() {
return x_stack.top();
}
int getMin() {
return min_stack.top();
}
};
lc206.翻转链表–简单
题目描述
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
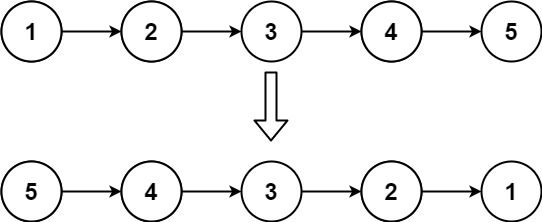
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
示例 2:
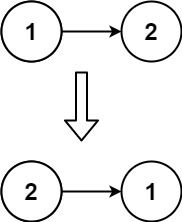
输入:head = [1,2]
输出:[2,1]
示例 3:
输入:head = []
输出:[]
提示:
- 链表中节点的数目范围是
[0, 5000] -5000 <= Node.val <= 5000
代码展示
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
ListNode last = null;
// 要改每条边,所以需要访问链表
while (head != null) {
ListNode nextHead = head.next;
// 改一条边
head.next = last;
// last, head向后移动一位
last = head;
head = nextHead;
}
return last;
}
}
lc227.基本计算器II–中等
题目描述
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
整数除法仅保留整数部分。
你可以假设给定的表达式总是有效的。所有中间结果将在 [-231, 231 - 1] 的范围内。
**注意:**不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。
示例 1:
输入:s = "3+2*2"
输出:7
示例 2:
输入:s = " 3/2 "
输出:1
示例 3:
输入:s = " 3+5 / 2 "
输出:5
提示:
1 <= s.length <= 3 * 105s由整数和算符('+', '-', '*', '/')组成,中间由一些空格隔开s表示一个 有效表达式- 表达式中的所有整数都是非负整数,且在范围
[0, 231 - 1]内 - 题目数据保证答案是一个 32-bit 整数
代码展示
class Solution {
public:
int calculate(string s) {
vector<int> stk;
char preSign = '+';
int num = 0;
int n = s.length();
for (int i = 0; i < n; ++i) {
if (isdigit(s[i])) {
num = num * 10 + int(s[i] - '0');
}
if (!isdigit(s[i]) && s[i] != ' ' || i == n - 1) {
switch (preSign) {
case '+':
stk.push_back(num);
break;
case '-':
stk.push_back(-num);
break;
case '*':
stk.back() *= num;
break;
default:
stk.back() /= num;
}
preSign = s[i];
num = 0;
}
}
return accumulate(stk.begin(), stk.end(), 0);
}
};
lc224.基本计算器–困难
题目描述
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。
示例 1:
输入:s = "1 + 1"
输出:2
示例 2:
输入:s = " 2-1 + 2 "
输出:3
示例 3:
输入:s = "(1+(4+5+2)-3)+(6+8)"
输出:23
提示:
1 <= s.length <= 3 * 105s由数字、'+'、'-'、'('、')'、和' '组成s表示一个有效的表达式- ‘+’ 不能用作一元运算(例如, “+1” 和
"+(2 + 3)"无效) - ‘-’ 可以用作一元运算(即 “-1” 和
"-(2 + 3)"是有效的) - 输入中不存在两个连续的操作符
- 每个数字和运行的计算将适合于一个有符号的 32位 整数
代码展示
class Solution {
public:
int calculate(string s) {
stack<char> ops;
vector<string> tokens;
long long val = 0;
bool num_started = false; // 是否正在parse一个数值,数值后面遇到第一个符号时,要把parse好的数存起来
bool needs_zero = true; // 是否需要补0,例如 "-48 + +48",要补成"0-48 + 0+48"
// leetcode这题不太严谨,官方 "1- -1"的答案是0,即"1-0-1",而不是1减去负1得2,大家不要在意细节,无脑补0就行了
for (char ch : s) {
// Parse一个数值
if (ch >= '0' && ch <= '9') {
val = val * 10 + ch - '0';
num_started = true;
continue;
} else if (num_started) { // 数值后面第一次遇到符号
tokens.push_back(to_string(val));
num_started = false;
needs_zero = false; // 加减号跟在数值后面,不需要补0,例如"10-1"
val = 0;
}
if (ch == ' ') continue;
// 处理运算符
if (ch == '(') {
ops.push(ch);
needs_zero = true; // 加减号跟在左括号后面,需要补零,例如"(-2)*3"变为"(0-2)*3"
continue;
}
if (ch == ')') {
while (ops.top() != '(') { // 两个括号之间的都可以计算了
// push back 包含一个符号的字符串
tokens.push_back(string(1, ops.top()));
ops.pop();
}
ops.pop();
needs_zero = false; // 加减号跟在右括号后面,不需要补0,例如"3*(1-2)+3"
continue;
}
// 处理+-*/
if (needs_zero) tokens.push_back("0"); // 补0
while (!ops.empty() && getRank(ops.top()) >= getRank(ch)) {
// 前面的符号优先级更高,就可以计算了,例如1*2+3,遇到+时,*就可以算了
tokens.push_back(string(1, ops.top()));
ops.pop();
}
ops.push(ch);
needs_zero = true; // +-后面跟着+-号,需要补0,例如"3 + -1",变为"3 + 0-1"
}
if (num_started) tokens.push_back(to_string(val));
while (!ops.empty()) { // 最后剩余的符号都要取出来
tokens.push_back(string(1, ops.top()));
ops.pop();
}
return evalRPN(tokens);
}
int getRank(char ch) {
if (ch == '+' || ch == '-') return 1;
if (ch == '*' || ch == '/') return 2;
return 0;
}
int evalRPN(vector<string>& tokens) {
stack<long long> s;
for (string& token : tokens) {
// is number
if (token == "+" || token == "-" || token == "*" || token == "/") {
long long b = s.top();
s.pop();
long long a = s.top();
s.pop();
s.push(calc(a, b, token));
} else {
s.push(stoi(token));
}
}
return s.top();
}
long long calc(long long a, long long b, string op) {
if (op == "+") return a + b;
if (op == "-") return a - b;
if (op == "*") return a * b;
if (op == "/") return a / b;
return 0;
}
};
lc283.移动零–简单
题目描述
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
提示:
1 <= nums.length <= 104-231 <= nums[i] <= 231 - 1
代码展示
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int n = 0;
// 主题思路:保留非零值
for (int i = 0; i < nums.size(); i++) {
if (nums[i] != 0) {
nums[n] = nums[i];
n++;
}
}
// 按题目要求,最后面填充零
while (n < nums.size()) {
nums[n] = 0;
n++;
}
}
};
lc641.设计循环双端队列–中等
题目描述
设计实现双端队列。
实现 MyCircularDeque 类:
MyCircularDeque(int k):构造函数,双端队列最大为k。boolean insertFront():将一个元素添加到双端队列头部。 如果操作成功返回true,否则返回false。boolean insertLast():将一个元素添加到双端队列尾部。如果操作成功返回true,否则返回false。boolean deleteFront():从双端队列头部删除一个元素。 如果操作成功返回true,否则返回false。boolean deleteLast():从双端队列尾部删除一个元素。如果操作成功返回true,否则返回false。int getFront()):从双端队列头部获得一个元素。如果双端队列为空,返回-1。int getRear():获得双端队列的最后一个元素。 如果双端队列为空,返回-1。boolean isEmpty():若双端队列为空,则返回true,否则返回false。boolean isFull():若双端队列满了,则返回true,否则返回false。
示例 1:
输入
["MyCircularDeque", "insertLast", "insertLast", "insertFront", "insertFront", "getRear", "isFull", "deleteLast", "insertFront", "getFront"]
[[3], [1], [2], [3], [4], [], [], [], [4], []]
输出
[null, true, true, true, false, 2, true, true, true, 4]
解释
MyCircularDeque circularDeque = new MycircularDeque(3); // 设置容量大小为3
circularDeque.insertLast(1); // 返回 true
circularDeque.insertLast(2); // 返回 true
circularDeque.insertFront(3); // 返回 true
circularDeque.insertFront(4); // 已经满了,返回 false
circularDeque.getRear(); // 返回 2
circularDeque.isFull(); // 返回 true
circularDeque.deleteLast(); // 返回 true
circularDeque.insertFront(4); // 返回 true
circularDeque.getFront(); // 返回 4
提示:
1 <= k <= 10000 <= value <= 1000insertFront,insertLast,deleteFront,deleteLast,getFront,getRear,isEmpty,isFull调用次数不大于2000次
代码展示
public class MyCircularDeque {
// 1、不用设计成动态数组,使用静态数组即可
// 2、设计 head 和 tail 指针变量
// 3、head == tail 成立的时候表示队列为空
// 4、tail + 1 == head
private int capacity;
private int[] arr;
private int front;
private int rear;
/**
* Initialize your data structure here. Set the size of the deque to be k.
*/
public MyCircularDeque(int k) {
capacity = k + 1;
arr = new int[capacity];
// 头部指向第 1 个存放元素的位置
// 插入时,先减,再赋值
// 删除时,索引 +1(注意取模)
front = 0;
// 尾部指向下一个插入元素的位置
// 插入时,先赋值,再加
// 删除时,索引 -1(注意取模)
rear = 0;
}
/**
* Adds an item at the front of Deque. Return true if the operation is successful.
*/
public boolean insertFront(int value) {
if (isFull()) {
return false;
}
front = (front - 1 + capacity) % capacity;
arr[front] = value;
return true;
}
/**
* Adds an item at the rear of Deque. Return true if the operation is successful.
*/
public boolean insertLast(int value) {
if (isFull()) {
return false;
}
arr[rear] = value;
rear = (rear + 1) % capacity;
return true;
}
/**
* Deletes an item from the front of Deque. Return true if the operation is successful.
*/
public boolean deleteFront() {
if (isEmpty()) {
return false;
}
// front 被设计在数组的开头,所以是 +1
front = (front + 1) % capacity;
return true;
}
/**
* Deletes an item from the rear of Deque. Return true if the operation is successful.
*/
public boolean deleteLast() {
if (isEmpty()) {
return false;
}
// rear 被设计在数组的末尾,所以是 -1
rear = (rear - 1 + capacity) % capacity;
return true;
}
/**
* Get the front item from the deque.
*/
public int getFront() {
if (isEmpty()) {
return -1;
}
return arr[front];
}
/**
* Get the last item from the deque.
*/
public int getRear() {
if (isEmpty()) {
return -1;
}
// 当 rear 为 0 时防止数组越界
return arr[(rear - 1 + capacity) % capacity];
}
/**
* Checks whether the circular deque is empty or not.
*/
public boolean isEmpty() {
return front == rear;
}
/**
* Checks whether the circular deque is full or not.
*/
public boolean isFull() {
// 注意:这个设计是非常经典的做法
return (rear + 1) % capacity == front;
}
}