【算法基础课】数组模拟栈、队列

一、数组模拟栈

1.思路

用数组模拟栈，可以帮助我们理解栈的本质。

模拟栈的关键点就是“栈顶指针”！这比链表简单多了，链表需要知道头尾、每个节点的前后指针，而栈只有一个指针！

随着不断地push和pop，栈顶指针会不断向后移动，前面的空间就浪费了。这对于算法题来说是可以忍受的，毕竟更看重时间效率。

2.代码模板

#include
#include
using namespace std;

const int N=1e6+10;
int m;
int stk[N],tt;//stk模拟栈，tt模拟栈顶指针

void clear(){
    tt=-1;//初始化，栈顶指针指向空
}
void push(int x){
    stk[++tt]=x;//栈顶指针+1，赋值新的栈顶元素
}
void pop(){
    tt--;//栈顶指针-1
}
bool empty(){
    if(tt>=0)cout<<"NO"<<endl;//栈顶指针不为空，栈就不为空
    else cout<<"YES"<<endl;
}
void query(){
    cout<<stk[tt]<<endl;//每次查询只能找到栈顶元素
}

int main(){
    scanf("%d",&m);
    clear();
    while(m--){
        string str;int x;
        cin>>str;
        if(str=="push"){
            cin>>x;
            push(x);
        }else if(str=="pop"){
            pop();
        }else if(str=="query"){
            query();
        }else if(str=="empty"){
            empty();
        }
    }
    //【遍历/依次弹出栈】
    while(tt>-1){
       cout<<stk[tt--]<<endl;
    }
    return 0;
}

3.进阶：单调栈

要求： 输出每个数字左边第一个比它小的数字。
思路： 暴力解法是，对于第i个数，从第i-1个数开始向左遍历，直到遇到一个比它小的数。我们可以这样一个性质，如果第i个数左边某个数比它大，那这个数永远不会被输出。对于i来说当然不能输出，对于i以后的数，也不会输出，所以可以直接删掉。

基于此，我们可以把数组中的每个数放入栈里面，对于新的数，如果栈顶比它大，就弹出。这样最后得到的就是一个单调递增的栈。当然，我们的答案也很容易就出来了。

代码模板

#include
using namespace std;

const int N=1e5+10;
int tt=-1,stk[N];

int main(){
    int n;cin>>n;
    for(int i=0;i<n;i++){
        int x;cin>>x;
        //查看栈，如果不为空，看栈顶元素是不是比它大，如果是，就弹出栈顶元素
        while(tt!=-1&&stk[tt]>=x)tt--;
        if(tt!=-1){//如果此时栈不为空，栈顶元素就是我们要找的最近的比x小的数
            cout<<stk[tt]<<" ";
        }else cout<<-1<<" ";
        stk[++tt]=x;
    }
    return 0;
}

二、数组模拟队列

1.思路

用数组模拟队列，关键是“队头指针”和“队尾指针”。队尾初始化为-1，随着不断添加元素，队尾指针不断向后移动，就像栈顶指针一样。而队头呢，在添加新元素的时候是不变的，所以一开始就要指向index为0的位置。

如果直接取队头的元素，此时队列可能为空。那怎么判断队列为空呢？直接判断队尾指针是否为-1吗？错了！要判断队尾指针和队头指针的关系，队列为空的时候队尾>队头。

随着不断地push、pop，队尾和队头的指针会不断地后移，前面的空间就浪费了。这对于算法题来说，是可以忍受的。当然还有循环队列这种解决方式。

2.代码模板

#include
#include
using namespace std;

const int N=1e6+10;
int q[N],hh=0,tt=-1;

void clear(){
    hh=0,tt=-1;
}
void push(int x){
    q[++tt]=x;//向队尾插入一个元素
}
void pop(){
    hh++;//初始时，设置队头>队尾。元素为1时，hh=tt=0。元素为2时，hh=0，tt=1；
}
void empty(){
    if(hh<=tt)cout<<"NO"<<endl;
    else cout<<"YES"<<endl;
}
bool isEmpty(){
    if(hh<=tt)return false;
    else return true;
}
void query(){
    if(!isEmpty())cout<<q[hh]<<endl;
}
int main(){
    int m;
    scanf("%d",&m);
    clear();
    while(m--){
        string str;int x;
        cin>>str;
        if(str=="push"){
            cin>>x;
            push(x);
        }else if(str=="pop"){
            pop();
        }else if(str=="query"){
            query();
        }else if(str=="empty"){
            empty();
        }
    }
    //【遍历/依次弹出队头元素】
    // while(!isEmpty()){
    //   cout<
    // }
    return 0;
}

3.进阶：单调队列

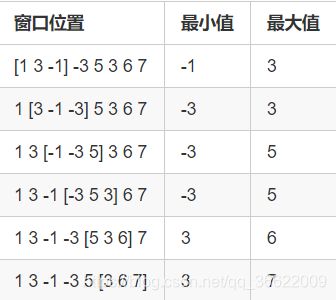
要求： 给定一个大小为n≤106的数组。有一个大小为k的滑动窗口，它从数组的最左边移动到最右边。您只能在窗口中看到k个数字。每次滑动窗口向右移动一个位置。您的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

思路： 暴力解法是，维护滑动窗口为一个普通队列，每次添加和删除一个数，并线性遍历，得到k个数中的最大值和最小值。然而我们可以这样一个性质，如果将一个新的数添加到滑动窗口中，若这个数左边某个数比它大，那该数永远不会被输出。所以我们可以把滑动窗口中比新的数大的数字都删掉。

基于此，滑动窗口就变成了一个单调递增的队列。队头是最小值，队尾是最大值。

代码模板

【注意】为什么要进行两次呢？因为每次只能得到该窗口的一种最值。比如，[1,3,-1],-3。当i==2，指向-1时，我们要求最小值，此时，我们已经把队列删的只剩下{-1}了。正确的最大值早就被删掉啦！

#include
using namespace std;

const int N=1e6+10;
int n,k;
int a[N],q[N];//原数组和滑动窗口队列

int main(){
    //【1】读入原数组的值
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++){
        scanf("%d",&a[i]);
    }
    //【2】输出最小值
    //<1>定义单调队列的头和尾指针
    int hh=0,tt=-1;
    
    //<2>遍历元素组中的每个元素
    for(int i=0;i<n;i++){
        
        //<3>去掉队头元素
        if(hh<=tt&&(q[hh]<i-k+1))hh++;//队列不为空，且，队头元素的index已经小于当前的index减去k的长度了。
        //比如，k=3.当i==3时，窗口为(1,2,3),i=0已经不在窗口中了。
        
        //<4>去掉队中的冗余元素
        while(hh<=tt&&a[q[tt]]>a[i]) tt--;//单调递增序列，左边的值应该小于等于右边的值才对
        
        //<5>添加队尾元素
        q[++tt]=i;
        
        //<6>到达第一个窗口时，输出最小值
        if(i>=k-1) printf("%d ",a[q[hh]]);
    }
    puts("");
    
    //【3】输出最大值
    hh=0,tt=-1;
    for(int i=0;i<n;i++){
        if(hh<=tt&&(q[hh]<i-k+1))hh++;
        while(hh<=tt&&a[q[tt]]<a[i]) tt--;//单调递减序列
        q[++tt]=i;
        if(i>=k-1)printf("%d ",a[q[hh]]);//队头是最大值
    }
    puts("");
    
    return 0;
}