第二章 数据结构(一)链表、栈、队列、单调栈、单调队列、KMP
1. 单链表
用数组模拟链表:单链表、双链表
用 e[i] 表示第 i 个节点的值,ne[i] 表示第 i 个节点下一个节点的下标。
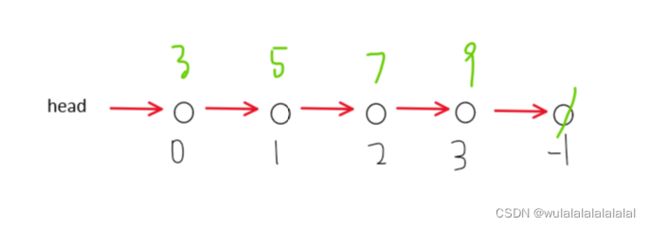
e[0] = 3 , ne[0] = 1;
…
e[3] = 9 , ne[3] = -1.
e和ne都是整数数组,空节点的下标用-1来表示,head表示第一个节点的下标。
// head 表示头节点的下标
// e[N] 表示节点 i 的值
// ne[i] 表示节点 i 下一个节点的下标
// idx 存储当前已经用到了哪个点 (尾节点的下一点,那个空的节点)
int head,e[N],ne[N],idx;
// 初始化
void init()
{
head = -1;
idx = 0;
}
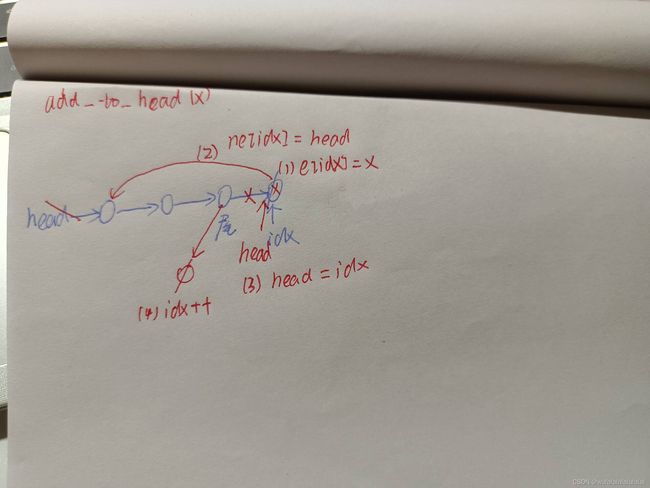
// 将x插到第一个结点前边
void add_to_head(int x)
{
e[idx] = x;
ne[idx] = head;
head = idx;
idx ++;
}
// 将 x 点插到下标是 k 的这个点的后边
void add_to_k(int k,int x)
{
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx;
idx ++;
}
// 将下标是k的点后面的点删掉
void remove_k(int k)
{
ne[k] = ne[ne[k]];
}
单链表:
实现一个单链表,链表初始为空,支持三种操作:
向链表头插入一个数;
删除第 k 个插入的数后面的数;
(删除第k-1个点)
在第 k 个插入的数后插入一个数。
(第k-1个点后面插入一个数)
现在要对该链表进行 M 次操作,进行完所有操作后,从头到尾输出整个链表。
注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。
例如操作过程中一共插入了 n 个数,则按照插入的时间顺序,
这 n 个数依次为:第 1 个插入的数,第 2 个插入的数,…第 n 个插入的数。
(第k个插入的数是k-1)
输入格式
第一行包含整数 M ,表示操作次数。
接下来 M 行,每行包含一个操作命令,操作命令可能为以下几种:
1. H x,表示向链表头插入一个数 x。
2. D k,表示删除第 k 个插入的数后面的数(当 k 为 0 时,表示删除头结点)。
3. I k x,表示在第 k 个插入的数后面插入一个数 x(此操作中 k 均大于 0)。
输出格式
共一行,将整个链表从头到尾输出。
输入样例:
10
H 9
I 1 1
D 1
D 0
H 6
I 3 6
I 4 5
I 4 5
I 3 4
D 6
输出样例:
6 4 6 5
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 100010;
// head 表示头节点的下标
// e[N] 表示节点 i 的值
// ne[i] 表示节点 i 下一个节点的下标
// idx 存储当前已经用到了哪个点 (尾节点的下一点,那个空的节点的下标)
int head,e[N],ne[N],idx;
// t指的是目前为止i次操作中,插入操作的次数
// 初始化
void init()
{
head = -1;
//head = 0;
idx = 0;
}
// 将x插到第一个结点前边
void add_to_head(int x)
{
e[idx] = x;
ne[idx] = head;
head = idx;
idx ++;
}
// 将 x 点插到下标是 k 的这个点的后边
void add_to_k(int k,int x)
{
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx;
idx ++;
}
// 将下标是k的点后面的点删掉
void remove_k(int k)
{
ne[k] = ne[ne[k]];
}
int main()
{
init();
int m;
cin >> m;
while(m--)
{
int k,x;
char op;
cin >> op;
if(op == 'H')
{
cin >> x;
add_to_head(x);
}
else if(op == 'D')
{
cin >> k;
if(k == 0)
head = ne[head];
remove_k(k-1);
}
else
{
cin >> k >> x;
add_to_k(k-1,x);
}
}
for(int i = head ;i != -1;i = ne[i])
cout << e[i] <<" ";
cout <<endl;
return 0;
}
2. 双链表
实现一个双链表,双链表初始为空,支持 5 种操作:
1.在最左侧插入一个数;
2.在最右侧插入一个数;
3.将第 k 个插入的数删除;
4.在第 k 个插入的数左侧插入一个数;
5.在第 k 个插入的数右侧插入一个数
现在要对该链表进行 M 次操作,进行完所有操作后,从左到右输出整个链表。
注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。
例如操作过程中一共插入了 n 个数,则按照插入的时间顺序,这 n 个数依次为:
第 1 个插入的数,第 2 个插入的数,… 第 n 个插入的数。
输入格式
第一行包含整数 M ,表示操作次数。
接下来 M 行,每行包含一个操作命令,操作命令可能为以下几种:
L x,表示在链表的最左端插入数 x。
R x,表示在链表的最右端插入数 x。
D k,表示将第 k 个插入的数删除。
IL k x,表示在第 k 个插入的数左侧插入一个数。
IR k x,表示在第 k 个插入的数右侧插入一个数。
输出格式
共一行,将整个链表从左到右输出。
数据范围
1≤M≤100000
所有操作保证合法。
输入样例:
10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2
输出样例:
8 7 7 3 2 9
【解析】
怎样理解“第 k 个插入的数”?
#include<iostream>
#include<string.h>
using namespace std;
const int N = 100010;
int m;
int e[N],l[N],r[N],idx;
// l表示每个点左边的点下标,r表示右边
// 初始化
void init()
{
// 0表示左端点,1表示右端点
// 0号点的右边是1号点,1号点的左边是0号点
// 0号点和1号点其实是两个边界,不用来存放数据
r[0] = 1;
l[1] = 0;
idx = 2;
// idx 表示现在可以使用下标为2的点存放你要存的数据
// 那么第一个插入的数下标就是2,第二个插入的数下标是3...第k个插入的数下标是k+1
}
//在下标是k点的右边插入一个点x
void add(int k,int x)
{
e[idx] = x;
r[idx] = r[k];
l[r[k]] = idx;
r[k] = idx;
l[idx] = k;
idx ++;
// 如果想在下标是k的点的左边插入x
// 其实就等于在下标是l[k]的右边插入x,add(l[k],x);
}
// 删除下标是k的点
void remove(int k)
{
r[l[k]] = r[k];
l[r[k]] = l[k];
}
// 在最左侧插入一个数
void addl(int x)
{
// 在下标是0的右边插入x
add(0,x);
}
// 在最右侧插入一个数
void addr(int x)
{
// 在下标是l[1]的右边插入x
add(l[1],x);
}
int main(void)
{
init();
cin >> m;
for(int i = 0;i < m;i++)
{
string op;
cin >> op;
if(op == "L")
{
int x;
cin >> x;
addl(x);
}
else if(op == "R")
{
int x;
cin >> x;
addr(x);
}
else if(op == "D")
{
int k;
cin >> k;
remove(k+1);
}
else if(op == "IL")
{
int k,x;
cin >> k >> x;
add(l[k+1],x);
}
else if(op == "IR")
{
int k,x;
cin >> k >> x;
add(k+1,x);
}
}
// cout<
for(int i = r[0];i != 1;i = r[i])
{
cout << e[i] << " ";
}
return 0;
}
3. 栈
#include<iostream>
using namespace std;
const int N = 100010;
int s[N];
int m,top=0;
// top 是栈顶指针,指向 0 的时候证明栈是空的
void push(int x)
{
s[++top] = x;
}
void pop(void)
{
top--;
}
string empty(void)
{
if(top == 0)
return "YES";
return "NO";
}
int query(void)
{
return s[top];
}
int main(void)
{
cin >> m;
for(int i = 0;i < m;i++)
{
string op;
cin >> op;
if(op == "push")
{
int x;
cin >> x;
push(x);
}
else if(op == "pop")
{
pop();
}
else if(op == "empty")
{
cout << empty() <<endl;
}
else if(op == "query")
{
cout << query() <<endl;
}
}
return 0;
}
4. 队列
#include<iostream>
using namespace std;
const int N = 100010;
int q[N];
int m,head=0,tail=0;
/* head指向队列的第一个元素,tail指向队列最后一个元素的后一个空位置,
可以用来放新入队的值
head == tail 的时候证明栈是空的 */
void push(int x)
{
q[tail++] = x;
}
void pop(void)
{
head++;
}
string empty(void)
{
if(head == tail)
return "YES";
return "NO";
}
int query(void)
{
return q[head];
}
int main(void)
{
cin >> m;
for(int i = 0;i < m;i++)
{
string op;
cin >> op;
if(op == "push")
{
int x;
cin >> x;
push(x);
}
else if(op == "pop")
{
pop();
}
else if(op == "empty")
{
cout << empty() <<endl;
}
else if(op == "query")
{
cout << query() <<endl;
}
}
return 0;
}
5. 单调栈 *****
给定一个长度为 N 的整数数列,输出每个数左边第一个比它小的数,如果不存在则输出 −1。
输入格式
第一行包含整数 N ,表示数列长度。
第二行包含 N 个整数,表示整数数列。
输出格式
共一行,包含 N 个整数,其中第 i 个数表示第 i 个数的左边第一个比它小的数,
如果不存在则输出 −1。
数据范围
1≤N≤10^5
1≤数列中元素≤10^9
输入样例:
5
3 4 2 7 5
输出样例:
-1 3 -1 2 2
【解析】
将输入的n个数存入栈,从栈底到栈顶依次为,a1,a2,a3,a4,a5,如果a3 >= a5,
那么a3永远不会作为答案输出来,因为我们要找的是左边第一个比它小的数。
也就是说,如果有ax >= ay,x<y,那么ax就可以被删掉。
那么最后剩下的这个栈就一定是单调栈。
#include<iostream>
using namespace std;
const int N = 100010;
int s[N];
int n,top=-1;
// 从 0 开始放,top指向栈顶
int main(void)
{
cin >> n;
for(int i = 0;i < n;i++)
{
int x;
cin >> x;
if(top == -1) // (1)如果当前栈是空的,前面没有比x小的,输出-1,x入栈
{
cout << "-1" <<" ";
s[++top] = x; // 把当前输入的x入栈
continue;
}
// (2)栈中有大于x的数,需要把这些大于x的数全部出栈,然后把栈顶的数输出,再把x入栈
else if(s[top] >= x)
{
// 栈从栈底到栈顶是单调递增的
while(s[top] >= x)
{
if(top == -1)
break;
top--;
}
if(top == -1)
{
cout << "-1" <<" ";
s[++top] = x;
continue;
}
}
// (3) 当前栈栈顶小于x,可以直接把栈顶输出,x入栈
cout << s[top] << " ";
s[++top] = x; // 把当前输入的x入栈
}
return 0;
}
6. 单调队列 *****
滑动窗口
给定一个大小为 n≤10^6 的数组。
有一个大小为 k 的滑动窗口,它从数组的最左边移动到最右边。
你只能在窗口中看到 k 个数字。
每次滑动窗口向右移动一个位置。
以下是一个例子:
该数组为 [1 3 -1 -3 5 3 6 7],k 为 3。
窗口位置 最小值 最大值
[1 3 -1] -3 5 3 6 7 -1 3
1 [3 -1 -3] 5 3 6 7 -3 3
1 3 [-1 -3 5] 3 6 7 -3 5
1 3 -1 [-3 5 3] 6 7 -3 5
1 3 -1 -3 [5 3 6] 7 3 6
1 3 -1 -3 5 [3 6 7] 3 7
你的任务是确定滑动窗口位于每个位置时,窗口中的最大值和最小值。
输入格式
输入包含两行。
第一行包含两个整数 n 和 k,分别代表数组长度和滑动窗口的长度。
第二行有 n 个整数,代表数组的具体数值。
同行数据之间用空格隔开。
输出格式
输出包含两个。
第一行输出,从左至右,每个位置滑动窗口中的最小值。
第二行输出,从左至右,每个位置滑动窗口中的最大值。
输入样例:
8 3
1 3 -1 -3 5 3 6 7
输出样例:
-1 -3 -3 -3 3 3
3 3 5 5 6 7
#include<iostream>
using namespace std;
const int N = 1000010;
int a[N],q[N];
// a 数组存输的n个数 ,q 是单调队列(滑动窗口),q中存的是a中的元素下标
int n,k;
int main(void)
{
scanf("%d%d",&n,&k);
for(int i = 0;i < n;i++) scanf("%d",&a[i]);
int h=0,t=-1; // h队头,t队尾
/*
输出每个滑动窗口最小值
q是单调递增队列
*/
for(int i=0;i<n;i++)
{
// 判断队头是否应该划出窗口
// h<=t:队列不为空
// i-q[h]+1 > k ,窗口中的元素个数超过了k个(窗口元素满了) ,说明q[h]应该出了窗口
if(h <= t && i-q[h]+1 > k) h++;
// 判断 :队列不为空 & 队尾大于等于要入队的 ,让队尾出
while(h <= t && a[q[t]] >= a[i]) t--;
q[++t] = i;
// 从 第 k-1 次开始(队列满了)就可以取最小的输出了
if(h <= t && i >= k-1) printf("%d ",a[q[h]]);
}
printf("\n");
h=0,t=-1;
// 归0
/*
输出每个滑动窗口最大值
q是单调递减队列
*/
for(int i=0;i<n;i++)
{
if(h <= t && i-q[h]+1 > k) h++;
// 判断 :队列不为空 & 队尾小于等于要入队的 ,让队尾出
while(h <= t && a[q[t]] <= a[i]) t--;
q[++t] = i;
// 从 第 k-1 次开始(队列满了)就可以取最大的输出了
if(h <= t && i >= k-1) printf("%d ",a[q[h]]);
}
return 0;
}
7. KMP
KMP字符串
给定一个模式串 S,以及一个模板串 P ,所有字符串中只包含大小写英文字母以及阿拉伯数字。
模板串 P 在模式串 S 中多次作为子串出现。
求出模板串 P 在模式串 S 中所有出现的位置的起始下标。
输入格式
第一行输入整数 N ,表示字符串 P 的长度。
第二行输入字符串 P。
第三行输入整数 M ,表示字符串 S 的长度。
第四行输入字符串 S。
输出格式
共一行,输出所有出现位置的起始下标(下标从 0 开始计数),整数之间用空格隔开。
数据范围
1≤N≤10^5
1≤M≤10^6
输入样例:
3
aba
5
ababa
输出样例:
0 2
// 一般做法,会超时
#include<iostream>
using namespace std;
const int N = 100010,M = 1000010;
char p[N],s[M];
int n,m;
int main(void)
{
cin >> n;
for(int i = 0;i < n;i++)
{
cin >> p[i];
}
cin >> m;
for(int i = 0;i < m;i++)
{
cin >> s[i];
}
int flag = 1;
for(int i = 0;i < m;i++)
{
flag = 1;
for(int t = i,j = 0;j < n;t++,j++)
{
if(s[t] != p[j])
{
flag = 0;
break;
}
}
if(flag == 1)
printf("%d ",i);
}
return 0;
}
KMP算法:
模板串p的next 数组:next[i] = j含义:p[1] ~ p[j] == p[i-j+1] ~ p[i];尽可能保证 j 最大。
 例如:p = “abababab”
例如:p = “abababab”
对应next: 0 0 1 2 3 4 5 6

#include<iostream>
using namespace std;
const int N = 100010,M = 1000010;
char p[N],s[M];
int ne[N];
int n,m;
int main(void)
{
cin >> n >> p+1 >> m >> s+1;
// 求 next 数组过程
for(int i = 2,j = 0;i <= n;i++)
{
while(j && p[i] != p[j+1]) j = ne[j];
if(p[i] == p[j+1]) j++;
ne[i] = j;
}
// kmp 匹配过程
for(int i = 1,j = 0;i <= m;i++) // 与 s[i] 匹配的是 p[j+1],所以i从1开始,j从0开始
{
// i是s上的指针,j 是p上的指针
// 什么时候不进入while循环:j已经退回到0,或者s[i]与p[j+1]相等
/*
while循环的作用就是:试探j能不能往下走一步,也就是s[i] 与 p[j+1]是否相等,不能往下走,就让p上的指针j往回退
*/
while(j && s[i] != p[j+1])
j = ne[j];
if(s[i] == p[j+1]) j++; // 如果j可以往下走一步,那就往下走
if(j == n)
{
// 匹配成功
cout << i-n << " ";
j = ne[j];
// 匹配成功,j=ne[j] 的作用:j已经走到了p的末尾,开始下一轮匹配,又是让j回溯最短的问题
}
}
}

