leetcode 446. 等差数列划分 II - 子序列 - 困难题目- 官方题解 - 动态规划 - DFS

题目来源：力扣（LeetCode）和传说
链接：https://leetcode-cn.com/problems
特别鸣谢：来自夸夸群的 醉笑陪公看落花@知乎，王不懂不懂@知乎，QFIUNE@csdn
感谢小伙伴们督促学习，一起进步

给你一个整数数组 nums ，返回 nums 中所有 等差子序列 的数目。

如果一个序列中 至少有三个元素 ，并且任意两个相邻元素之差相同，则称该序列为等差序列。

例如，[1, 3, 5, 7, 9]、[7, 7, 7, 7] 和 [3, -1, -5, -9] 都是等差序列。
再例如，[1, 1, 2, 5, 7] 不是等差序列。
数组中的子序列是从数组中删除一些元素（也可能不删除）得到的一个序列。

例如，[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。
题目数据保证答案是一个 32-bit 整数。

示例 1：

输入：nums = [2,4,6,8,10]
输出：7
解释：所有的等差子序列为：
[2,4,6]
[4,6,8]
[6,8,10]
[2,4,6,8]
[4,6,8,10]
[2,4,6,8,10]
[2,6,10]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/arithmetic-slices-ii-subsequence

官方题解分析

• 用字典存储任意两个元素的差值
• 如果这个等差之前被存储过，说明至少有三个元素，可以构成等差序列
• 在前面构成的每个数列中增加一个元素，即可得到以当前元素结尾的等差数列

示意图如下：
动态转移数组 f[j][i] 表示以 nums[i] 结尾的动态数组个数+1

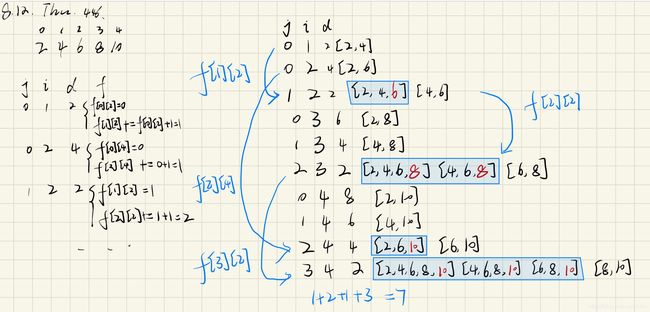
解题代码

class Solution:
    def numberOfArithmeticSlices(self, nums):
        def solve3(nums):
            f = [defaultdict(int) for _ in nums]
            ans = 0
            for i in range(len(nums)):
                for j in range(i):
                    d = nums[i]-nums[j]
                    ans += f[j][d]
                    f[i][d] += f[j][d]+1
            return ans
        
        return solve3(nums)

求子集，再求等差数列

先用交换的思想求子集 O(n!+(n-1)!+(n-2)!+… + 2! + 1)，再判断子集是否是等差数列 O(n)

整体时间复杂度 O((n!+(n-1)!+(n-2)!+… + 2! + 1) * n)

优化

• 加入备忘录，减少重复计算
• 优化子集判断为O(1) ， 深度遍历时，如果前面得到了[2,4,6]，后面增加一个 10 的时候，只需要判断 4，6，10 是否等差，即，只需要判断一次
• 交换位的前一个 i-1 位置比交换后位置j 的数字大，一定不能形成等差数列，直接跳过

优化之后的时间复杂度 O((2^n)-1)

交换的思想求子集

参考 leetcode 46 和47 . 全排列,两种生成树的方案来解决全排列问题

基础代码实现 - 超时

'''
超时 O((2^n)-1) * O(n)
'''

class Solution:
    def numberOfArithmeticSlices(self, nums):
        self.count = 0
        memor = set()
        def solve1(nums):
            nums.sort()
            dnums = [(v,i) for i,v in enumerate(nums)]
            DFS(dnums,0)
        def DFS(dnums,i):
            if i == len(dnums):return
            for j in range(i,len(nums)):
                if dnums[i][1] > dnums[j][1] or (i>0 and dnums[i-1][1]>dnums[j][1]):
                    continue
                dnums[i],dnums[j] = dnums[j],dnums[i]
                if i>=2 and tuple(dnums[:i+1]) not in memor and check(dnums,i):
                    self.count += 1
                    memor.add(tuple(dnums[:i+1]))
                DFS(dnums,i+1)
                dnums[i],dnums[j] = dnums[j],dnums[i]
        def check(dnums,i):
            for j in range(1,i):
                if dnums[j+1][0]-dnums[j][0] != dnums[j][0]-dnums[j-1][0]:
                    return False
            return True
        solve1(nums)
        return self.count

代码实现- 优化等差数列检查 - 还有点错误

'''
优化等差数列判断 - 超时
超时 O((2^n)-1) * O(1)
'''
class Solution:
    def numberOfArithmeticSlices(self, nums):
        self.count = 0
        memor = set()
        def solve1(nums):
            nums.sort()
            dnums = [(v,i) for i,v in enumerate(nums)]
            DFS(dnums,0,False)
        def DFS(dnums,i,dc):
            if i == len(dnums):return
            for j in range(i,len(nums)):
                if dnums[i][1] > dnums[j][1] or (i>0 and dnums[i-1][1]>dnums[j][1]):
                    continue
                dnums[i],dnums[j] = dnums[j],dnums[i]
                dc = check(dnums,i,dc)
                if i>=2 and tuple(dnums[:i+1]) not in memor and dc:
                    self.count += 1
                    memor.add(tuple(dnums[:i+1]))
                DFS(dnums,i+1,dc)
                dnums[i],dnums[j] = dnums[j],dnums[i]
        def check(dnums,i,dc):
            if not dc and i>2:return False
            return dnums[i][0]-dnums[i-1][0] == dnums[i-1][0]-dnums[i-2][0]
        solve1(nums)
        return self.count

求某一个起点开始能构成的等差数列 DFS

todo