Java数据结构 | 二叉树的基本操作

 

目录

一、二叉树的存储方式

二、二叉树的遍历

前序遍历

中序遍历

后序遍历　

层序遍历

 三、二叉树的其他操作

获取树中节点的个数

获取树中叶子节点的个数

获取第k层节点的个数

获取二叉树的深度

---

一、二叉树的存储方式

二叉树可以链式存储，也可以顺序存储。

那么链式存储方式就用指针， 顺序存储的方式就是用数组。

顾名思义就是顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在散落在各个地址的节点串联一起。

链式存储如图：

链式存储是大家很熟悉的一种方式，那么我们来看看如何顺序存储呢？

其实就是用数组来存储二叉树，顺序存储的方式如图：

用数组来存储二叉树如何遍历的呢？

如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。

所以大家要了解，用数组依然可以表示二叉树。

二、二叉树的遍历

如果按照某种规则进行约定，则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点，L代表根节点的左子树，R代表根节点的右子树，则根据遍历根节点的先后次序有以下遍历方式：

NLR：前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。 LNR：中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。 LRN：后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点

层序遍历：从二叉树的根节点出发，首先访问第一层的节点，然后从左至右访问第二层的节点，从上至下，以此类推

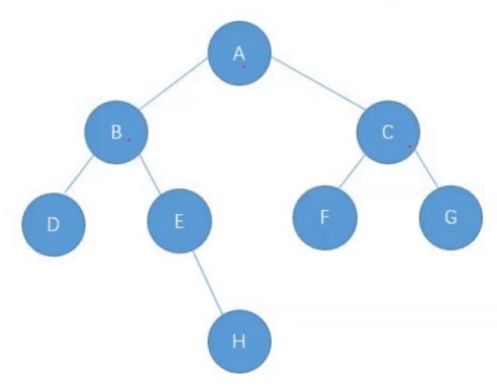
以上树为例，简单介绍二叉树的遍历实现：

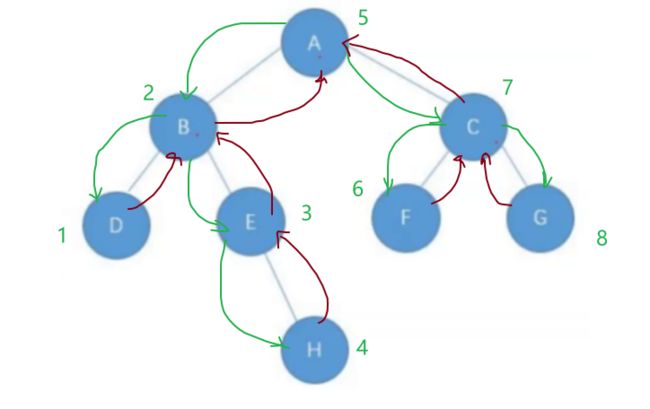
• 前序遍历

根节点－左子树－右子树

前序遍历的结果为： A　B　D　E　H　C　F　G

//前序遍历
   public void preOrder(TreeNode root){
        if(root == null){
            return;
        }
        System.out.println(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
​
   }

• 中序遍历

左子树－根节点－右子树

中序遍历的结果为： D B E 　H A F C G　

// 中序遍历
    public void inOrder(TreeNode root){
        if(root == null){
            return;
        }
        inOrder(root.left);
        System.out.println(root.val+" ");
        inOrder(root.right);
    }

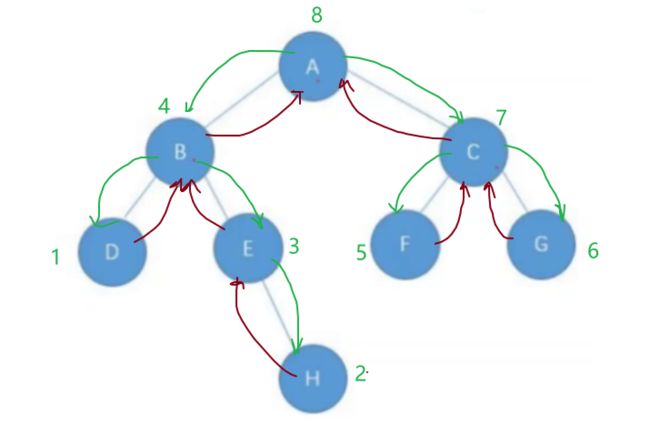
• 后序遍历　

左子树－右子树－根节点

 // 后序遍历
    public void postOrde(TreeNode root){
        if(root == null){
            return;
        }
        postOrde(root.left);
        postOrde(root.right);
        System.out.println(root.val+" ");
    }

• 层序遍历

从根节点出发从左至右，以此类推

层序遍历结果： A 　B 　C 　D 　E 　F　 G 　H

二叉树后序遍历的特点：最后一个节点肯定是根节点。

二叉树先序遍历的特定：第一个节点肯定是根节点。

• 使用List存储节点元素进行前序遍历

  public List preOrder2(TreeNode root){
        List ret = new ArrayList<>();
        if(root == null){
            return ret;
        }
        ret.add(root.val);
        List leftTree = preOrder2(root.left);
        ret.addAll(leftTree);
        List rightTree  = preOrder2(root.right);
        ret.addAll(rightTree);
        return ret;
    }

 三、二叉树的其他操作

• 获取树中节点的个数

获取树中节点的个数，我们可以采用遍历的方法实现，也可以采用子问题的思路，使用递归的方法，即左子树＋右子树＋根节点（＋１）即可实现

size(root.left) +size(root.right)+1; 

   /**
     *  遍历方法
     */
    public static int nodeSize = 0;
    public int size(TreeNode root){
        if(root == null){
            return 0;
        }
        nodeSize++;
        size(root.left);
        size(root.left);
        return nodeSize;
    }
    /**
     * 子树相加再加上根节点
     * @param root
     * @return
     */
    public int size2(TreeNode root){
        if(root == null){
            return 0;
        }
        int tmp = size(root.left) +size(root.right)+1;
        return tmp;
    }

• 获取树中叶子节点的个数

获取树中叶子节点的个数，即左子树和右子树都为空时root.left==null&&root.right==null时，左子树上叶子节点+右子树上所有的叶子节点 或者使用临时变量leafSize＋＋；

 /**
     * 获取叶子节点的个数
     * @param root
     * @return
     */
  //子问题思路
    public int getLeafNodeCount(TreeNode root){
        if(root == null){
            return  0;
        }
        if(root.left==null&&root.right==null){
            return 1;
        }
        int tmp = getLeafNodeCount(root.left)+getLeafNodeCount(root.right);
        return tmp;
    }
     //遍历方法
    public static int leafSize = 0;
    public  int getLeafNodeCount2(TreeNode root){
        if(root == null){
            return 0;
        }
        if(root.left == null&&root.right == null){
            leafSize++;
        }
        getLeafNodeCount2(root.left);
        getLeafNodeCount2(root.right);
        return leafSize;
    }

• 获取第k层节点的个数

求第k层节点的个数，可以转化为左树的 k-1 层 + 右树的k -1 层，即

当K=3时，转化为左树的第 2层和右树的第2层的节点个数，最后转化为当 k = 1时，返回左数第二层的节点2和右数第二层的节点2相加即可得到 第3 层的节点个数为4

 public int getKLevelNodeCount(TreeNode root,int k){
        if(root == null|| k <= 0){
            return 0;
        }
        if(k==1){
            return 1;
        }
     int tmp = getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);
      return tmp;
    }

• 获取二叉树的深度

public int getHeight(TreeNode root){
        if(root == null){
            return 0;
        }
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        //左右子树的最大c
        return leftHeight > rightHeight ? leftHeight+1 : rightHeight +1;
   }