单调栈介绍和使用

前言：

今天来讲一下单调栈，它定义是非常简单的，首先栈是一种先进后出、后进先出的数据结构。而单调栈，就是说栈中的元素是严格单调递增或者递减的。它主要用来解决的问题：找到前一个或者后一个的最大或者最小元素。属于一种空间换时间的思想，通常用来把O(n^2)的时间复杂度降低到O(n)。

典型的做法：

假设我们是要找比当前元素大的元素，那么栈内的元素就是递增的（从栈顶往栈底方向）。

当元素大于栈顶的元素，就把栈顶的元素给替换成当前元素；

当元素小于等于栈顶元素，就直接入栈。

这样处理后，栈内就一直保持着一个从栈顶往栈底方向递增的单调栈。

注意：一般栈内储存的都是元素的下标而不是元素的值，因为下标可以直接找到值，而值不能直接找到下标。

所以如果是计算两个元素之间的距离的题目，储存值就没法算了。

因此单调栈里面说的单调性指的是下标对应的元素值单调的。

实例：

LeetCode：739-每日温度

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]

示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]
 

提示：
1 <= temperatures.length <= 105
30 <= temperatures[i] <= 100

首先这道题，朴素的想法就是暴力处理，就是数组temperatures里面每个元素遍历一遍，假设右边第一个大于自己的元素下标是j，当前元素下标是i，然后j-i的值放入到answer[i]中就可以了。因为有n个元素，所以时间复杂度是O(n^{2)，空间复杂度就是开辟的answer数组，是O(n)。这样做在数据量比较小的时候是可以的，如果temperaturess长度到达了10}9这种，就会超时。

如果我们使用单调栈，就可以将时间复杂度降低到O(n)，但是同时要开辟一个n长度的栈，空间复杂度上升了。所以说单调栈是一种用空间换时间的做法，不过一般题目空间的要求都不高，对时间要求比较高，而且只开辟了一个n长度的栈，占用也不大，因此单调栈还是很实用的。

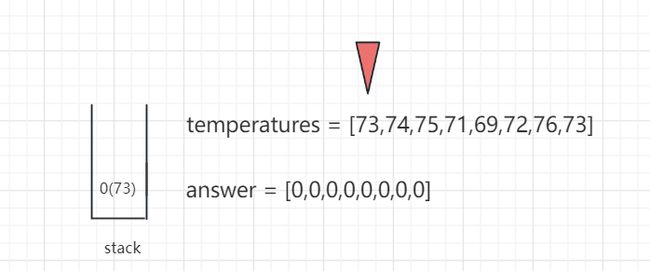
我们看一下这道题是怎么用单调栈处理的，以示例1为例子：

我们创建了一个栈stack

1.遍历到下标0，值73，栈是空的，0入栈

2.遍历到下标1，值74，发现74大于栈顶元素0对应的值73,

下标0出栈，下标1-下标0等于1，放入到answer[0]

下标1入栈

3.遍历到下标2，值75，发现75大于栈顶元素1对应的值是74,

下标1出栈，下标2-下标1等于1，放入到answer[1]

下标2入栈

4.遍历到下标3，值71，发现71小于栈顶元素2对应的值是75，下标3入栈

5.遍历到下标4，值69，发现69小于栈顶元素3对应的值是71，下标4入栈

6.遍历到下标5，值72，发现72大于栈顶元素4对应的值是69，下标4出栈

下标5-下标4等于1，放入到answer[4]

发现72大于栈顶元素3对应的值71，下标3出栈

下标5-下标3等于2，放入到answer[3]

发现72小于栈顶元素2对应的值75，下标5入栈

7.遍历到下标6，值76，发现76大于栈顶元素5的值72，栈顶元素5出栈

下标6-下标5等于1，放入到answer[5]

发现76大于栈顶元素2的值75，栈顶元素2出栈

下标6-下标2等于4，放入到answer[2]

栈内没有元素了，下标6入栈

8.遍历到下标7，值73，发现73小于栈顶元素6的值76，下标7入栈。

9.最后因为answer默认值是0，下标7和下标6没有

代码

public class DailyTemperatures_739 {


    public int[] dailyTemperatures(int[] temperatures) {
        Stack<Integer> stack = new Stack<>();
        int[] answer = new int[temperatures.length];
        for (int i = 0; i < temperatures.length; i++) {
            // 当前元素大于栈顶元素
            while (!stack.isEmpty() && temperatures[stack.peek()] < temperatures[i]) {
                int index = stack.pop();
                answer[index] = i - index;

            }
            // 栈是空的 或者 当前元素小于或者等于栈顶 就放入栈中
            stack.push(i);
        }
        return answer;
    }
    
}

代码其实很简单，但是要想到用单调栈来解决类似的问题，还需要多练习，因为很多题目不会直接说就是要找后面比当前元素大的元素，需要自己理解题意之后判断出来。

练习

再看一道单调栈的题目，LeetCode-美丽塔II-2866是上上周周赛的一道题目。

给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。
你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ，高度为 heights[i] 。
如果以下条件满足，我们称这些塔是 美丽 的：

1 <= heights[i] <= maxHeights[i]
heights 是一个 山状 数组。
如果存在下标 i 满足以下条件，那么我们称数组 heights 是一个 山状 数组：

对于所有 0 < j <= i ，都有 heights[j - 1] <= heights[j]
对于所有 i <= k < n - 1 ，都有 heights[k + 1] <= heights[k]
请你返回满足 美丽塔 要求的方案中，高度和的最大值 。

 

示例 1：
输入：maxHeights = [5,3,4,1,1]
输出：13
解释：和最大的美丽塔方案为 heights = [5,3,3,1,1] ，这是一个美丽塔方案，因为：
- 1 <= heights[i] <= maxHeights[i]  
- heights 是个山状数组，峰值在 i = 0 处。
13 是所有美丽塔方案中的最大高度和。

示例 2：
输入：maxHeights = [6,5,3,9,2,7]
输出：22
解释： 和最大的美丽塔方案为 heights = [3,3,3,9,2,2] ，这是一个美丽塔方案，因为：
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山状数组，峰值在 i = 3 处。
22 是所有美丽塔方案中的最大高度和。

示例 3：
输入：maxHeights = [3,2,5,5,2,3]
输出：18
解释：和最大的美丽塔方案为 heights = [2,2,5,5,2,2] ，这是一个美丽塔方案，因为：
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山状数组，最大值在 i = 2 处。
注意，在这个方案中，i = 3 也是一个峰值。
18 是所有美丽塔方案中的最大高度和。
 

提示：
1 <= n == maxHeights <= 105
1 <= maxHeights[i] <= 109

解析：

这个题目就没法直接看出来是用单调栈，要分析题目之后才能想到，因为要得到一个山状数组，山顶的左边是严格递增的，山的右边是严格递减的。所以我们可以用两次单调栈来解决这个问题，同时因为这个题目最后求得是元素的和，所以我们还需要两个数组来储存前缀和和后缀和，最大值就是前缀和pre数组和后缀和surf相加的最大值。

我们先假设山顶在最右边，前缀和的数组pre，就要储存从0到n-1的严格递增的前缀和，用stack来处理遍历过程中的元素。如果栈顶元素是比当前元素要大的，就说明当前元素小于栈顶元素值，要保持严格递增，就需要把原来stack中得元素全部弹出去，以当前元素作为山顶。

stack中有值的情况：

前缀和 = 小于等于当前元素的和 + （被弹出元素到当前元素的距离）* 当前元素值

stack中没有元素的情况：

前缀和 = 当前元素值 * （当前元素下标 + 1）， 这里可以想象如果数组maxHeights是3,2，那么就是2 * （下标 1 + 1）

计算完左边的数组之后，在计算右边的，右边本来是严格递减，但是如果我们从右往左遍历也跟pre数组一样是严格递增。

方便处理我们就改完总有往左遍历，只不过反过来处理下标的时候要注意一下。

最后就是Java会有溢出的情况，要注意下int到long的转换，要不然就会收到几发WA。

public class BeautifulTowersII_2866 {

    public long maximumSumOfHeights(List maxHeights) {
        if (maxHeights.size() == 1) {
            return maxHeights.get(0);
        }
        Stack stack = new Stack<>();
        int n = maxHeights.size();
        long ans = 0;
        long[] pre = new long[n];
        // 山状数组左边的递增数组 栈顶到栈底是递减的
        for (int i = 0; i < n; i++) {
            // 栈不为空 并且 栈顶元素是大于当前元素就要处理
            while(!stack.isEmpty() && maxHeights.get(stack.peek()) > maxHeights.get(i)) {
                stack.pop();
            }

           if (!stack.isEmpty()) {
               int t = stack.peek();
               pre[i] = pre[t] + (long)(i - t) * maxHeights.get(i) ;
           } else {
               pre[i] = (long)(i + 1) * maxHeights.get(i) ;
           }

            stack.push(i);

        }

        stack.clear();
        long[] surf = new long[n];
        // 山状数组的右边 递减数组 栈顶到栈底是递增的 我们从右往左遍历就可以和pre数组一样的处理方式
        for (int i = n - 1; i >= 0; i--) {
            while(!stack.isEmpty() && maxHeights.get(stack.peek()) > maxHeights.get(i)) {
                 stack.pop();
            }

            if (!stack.isEmpty()) {
                int t = stack.peek();
                surf[i] = surf[t] + (long)(t - i) * maxHeights.get(i) ;
            } else {
                surf[i] = (long)(n - i) * maxHeights.get(i) ;
            }

            stack.push(i);

        }

        for (int i = 0; i < n - 1; i++) {
            ans = Math.max(ans, pre[i] + surf[i+1]);
        }
        return ans;
    }
}

相关题目：

题目	难度
496. 下一个更大元素 I	简单
503. 下一个更大元素 II	中等
581. 最短无序连续子数组	中等
654. 最大二叉树	中等
316. 去除重复字母	中等
402. 移掉 K 位数字	中等
456. 132 模式	中等
42. 接雨水	困难
84. 柱状图中最大的矩形	困难
321. 拼接最大数	困难