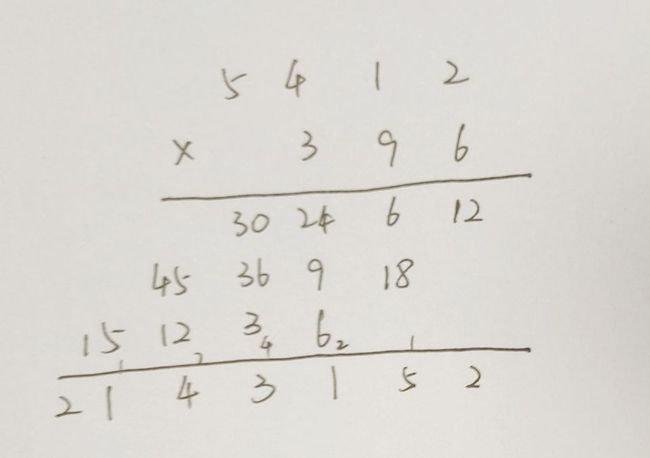程序设计-红皮书代码题记录

目录

讲义P25-将一个正整数分解质因数

写法一 

写法二

讲义P30-辗转相除法 

讲义P32-给出年月日，计算该日是该年的第几天

讲义P56-进制转换讲解

讲义P59-打印集合M的前面100个最小数（多路归并）

题目及思路讲解

仿照归并排序的写法一

代码更为简洁的写法二

讲义P61-输入正整数n，打印集合的所有子集 

讲义P67-求所有元素个数为M的子集 

讲义P68-实现任意两个不同进制非负整数之间的转换

实现输入多组数据

本题代码

讲义P80-交换两个向量的位置 

讲义P88-两个机器人的对话

讲义P91-对n个字符串按字典序排序

字符数组的相关操作

指针变量与变量指针 

本题代码

讲义P92-将0元素移动到数组后面，非0元素保持有序

讲义P93-删除数组中值在x到y之间的所有元素

讲义P95-删除数组中值相同的元素

讲义P101-用数组精确计算M/N的各小数位的值

讲义P105 生成螺旋矩阵

讲义P106 二维数组排序

冒泡排序版

插入排序版 

归并排序版

讲义P118-统计各个字符在字符串S中出现的次数

使用数组作为函数参数、函数返回值的问题

本题代码

讲义P121-输出s的值，精度1e-6

将整型赋值给浮点型的问题

本题代码

讲义P122-输出魔方阵

使用malloc动态创建二维数组

本题代码 

讲义P127-计算调和级数的前n项和

讲义P130 && 讲义P136-计算sinx的近似值

讲义P137-由小到大输出所有最简真分数

讲义P144-最大的三角形面积

讲义P146-寻找相切的圆

讲义P149-用二分法求方程的根

二分法

本题代码

讲义P150-用牛顿迭代法求方程的根

牛顿迭代法

本题代码

讲义P151-判断点是否在三角形内

用叉乘判断某点是否在三角形内

本题代码

讲义P153-面积最大的多组三角形

讲义P170-节点i经k步能到达的所有节点

C语言文件操作

讲义P173-用从文件中读取成绩信息，存入链表并排序

feof()函数多读一次的问题

关于fscanf()读取数据时的问题

本题代码

讲义P175-将学生信息存入链表，并写入文件中

讲义P177-冒泡法实现单向链表的排序

讲义P181-转换字符串并写入文件-练习4种文件读写方式

讲义P183-将链表中的所有数字串到前面，所有字母串到后面

用scanf读取字符的问题

本题代码

讲义P185-CCF会员信息排序

讲义P191-创建学生信息链表，删除特定年龄的学生信息

讲义P195-递归排序两个学生成绩链表

补充-用两个数组实现整数相乘

方法一

方法二

补充-打印特殊的二维数组

补充-由二进制数字组成的环

补充-计算组合数

补充-读取文件中的购物记录，计算购物总开销

---

讲义P25-将一个正整数分解质因数

示例：

写法一 

int main()
{
    int i, n;
    cout << "请输入一个数：";
    cin >> n;
    cout << n << " = ";
    //为什么需要i++？比i小的数难道不能是新的n的质因子吗？
    //答案是不会，因为如果比i小的数如果是n的质因子，那早就已经被分解掉了
    //实际上在这个算法中，被分解的质因子是从小到大递增的
    for (i = 2; i < n; i++)
    {
        while (n != i)  //若n == i，则n的质因数就是n本身
        {
            //这里不需要判断i是否为质数，因为根据这个算法的特性，在遇到i之前，n中关于i的因数都已经被分解掉了，
            //例如在将6作为因数之前必定已经将这个6分解为了2*3，在将9作为因数之前必定已经将9分解为了3*3
            //因此这里的i一定是个质数
            if (n % i == 0) //若i是质因数，则打印i
            {
                cout << i << " * ";
                n = n / i;
            }
            else break;     //若n不能被i整除，则考虑i + 1
        }
    }
    cout << n;  //打印最后一个质因数，也就是当n == i时的质因数
    return 0;
}

 打印如下：

写法二

上面的那种写法实在是和我不合，老是忘了怎么写，换下面这种写法好记点。

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 2; i <= n; i++)
    {
        while (n % i == 0)
        {
            printf("%d", i);
            n /= i;
            if (n != 1) printf(" * ");      //当最后剩个1时，说明已经分解完毕，不用再加乘号了
        }
    }
    return 0;
}

讲义P30-辗转相除法 

求a和b的最大公因数，也可以用来判断a和b是否互质

非递归写法：

int gcd(int a, int b)
{
    int r;
    while (b != 0)
    {
        r = a % b;
        a = b;
        b = r;
    }
    return a;
}

更为简便的递归写法：

int gcd(int a, int b)
{
    return b == 0 ? a : gcd(b, a % b);
}

讲义P32-给出年月日，计算该日是该年的第几天

按讲义上的写法来的，主要是在于数据的健壮性判断十分繁琐

/*
非整百年：能被4整除的为闰年。
整百年：能被400整除的是闰年。
*/
int is_leapyear(int year)
{
    if (year % 400 == 0 || year % 4 == 0 && year % 100 != 0)
    {
        return 1;
    }
    return 0;
}
 
//判断该日是今年的第几天
int whichday(int year, int month, int day)
{
    int mon[13] = { 0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 };
    mon[2] += is_leapyear(year); //如果是闰年，二月份就加1天
    int count = 0;
    for (int i = 1; i < month; i++)
    {
        count += mon[i];
    }
    count += day;
    return count;
}
 
int main()
{
    int year, month, day;
    cout << "请输入年份" << endl;
    while (1)
    {
        cin >> year;
        if (year < 0)
        {
            cout << "月份必须非负，请重新输入" << endl;
            continue;
        }
        break;
    }
 
    cout << "请输入月份" << endl;
    while (1)
    {
        cin >> month;
        if (month < 1 || month > 12)
        {
            cout << "月份必须在1到12之间" << endl;
            continue;
        }
        break;
    }
 
    cout << "请输入天数" << endl;
    while (1)
    {
        cin >> day;
        if (day < 1)
        {
            cout << "天数不能小于1" << endl;
            continue;
        }
        if (month == 1 || month == 3 || month == 5 || month == 7 || month == 8 || month == 10 || month == 12)
        {
            if (day > 31)
            {
                cout << "您输入的天数大于" << month << "月的最大天数" << endl;
                continue;
            }
        }
        else if (month == 2)
        {
            if (is_leapyear(year) == 1 && day > 29) //如果是闰年的话
            {
                cout << "您输入的天数大于" << month << "月的最大天数" << endl;
                continue;
            }
            else if (is_leapyear(year) == 0 && day > 28)    //如果不是闰年的话
            {
                cout << "您输入的天数大于" << month << "月的最大天数" << endl;
                continue;
            }
        }
        else
        {
            if (day > 30)
            {
                cout << "您输入的天数大于" << month << "月的最大天数" << endl;
                continue;
            }
        }
        break;
    }
    printf("%d年%d月%d日是该年的第%d天", year, month, day, whichday(year, month, day));
    return 0;
}

讲义P56-进制转换讲解

讲义P59-打印集合M的前面100个最小数（多路归并）

首先，关于多路归并的思想参考此处：【多路归并】从朴素优先队列到多路归并 (qq.com)

题目及思路讲解

讲义上的代码写得不好，于是在网上搜到了这一种很有意思的写法，该写法采用了归并排序的思想。

该题的难点在于很难确定最小的n个数到底是哪n个数，现在我们假设可以将int型变量的y和z看成两个"数组"：

                y记录的是 2 * a[0] + 1、 2 * a[1] + 1、 2 * a[2] + 1 ....

                z记录的是 3 * a[0] + 1、 3 * a[1] + 1、 3 * a[2] + 1 ....

只要a是个递增数组，y和z也显然都是递增"数组"，之后就可以利用归并排序的思想，每次对比y和z的大小，选取较小值入a数组，然后更新y或z的值。

这里还需要用到 i 指针和 j 指针，这两个指针其实都是a数组中的指针，只不过 i 是关于y“数组”的指针 ：y = 2 * a[i] + 1，j 是关于z“数组”的指针：z = 3 * a[j] + 1。

例如一开始 i = 0，a[0] = 1，于是 y = 2 * a[0] + 1 = 3；当3被选取成为a[1]之后，y“数组”就应该向后移一位了，于是 i = i + 1 = 1，a[1] = 3，y = 2 * a[1] + 1 = 7。j 指针同理。

仿照归并排序的写法一

这里是仿照我自己的归并排序的模板来写的，有助于理解

#define maxsize 100
int main()
{
    int a[maxsize];
    a[0] = 1;
    int y = 3, z = 4;   //y"数组"的首元素为2 * a[0] + 1 = 3，z"数组"的首元素为3 * a[0] + 1 = 4
    int i = 0, j = 0;
    //类似归并排序
    for (int k = 1; k < 100; k++)    //a[0]已经确定是1了，现在从第二位数a[1]开始确定后面的数字
    {
        if (y < z)
        {
            a[k] = y;
            i++;
            y = 2 * a[i] + 1;   //y"数组"移动到下一个元素
        }
        else if (y == z)        //由于集合的互异性，所以当出现两边的值相等时只取一个，两边的"数组"都移动
        {
            a[k] = y;
            i++;
            y = 2 * a[i] + 1;
            j++;
            z = 3 * a[j] + 1;
        }
        else if (y > z)
        {
            a[k] = z;
            j++;
            z = 3 * a[j] + 1;   //z"数组"移动到下一个元素
        }
    }

    for (int k = 0; k < 100; k++)
    {
        if (k % 10 == 0) printf("\n");
        printf("%4d ", a[k]);
    }
    return 0;
}

代码更为简洁的写法二

思路是一样的，不过这种写法更加简洁好看

int main()
{
    int a[100];
    a[0] = 1;

    for (int i = 0, j = 0, k = 1; k < 100; k++)
    {
        int y = 2 * a[i] + 1, z = 3 * a[j] + 1;
        a[k] = y < z ? y : z;    //y和z中较小的一个数作为a[k]
        //下面这两句的写法很妙，可以方便地将y < z 、 y == z 、 y > z这三种情况统一起来，不会像写法一那样麻烦
        if (y == a[k]) i++;
        if (z == a[k]) j++;
    }

    for (int k = 0; k < 100; k++)
    {
        if (k % 10 == 0) printf("\n");
        printf("%4d ", a[k]);
    }
    return 0;
}

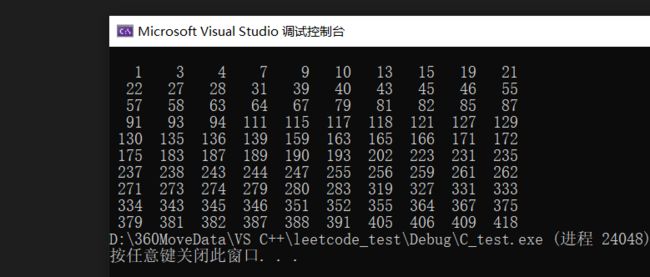
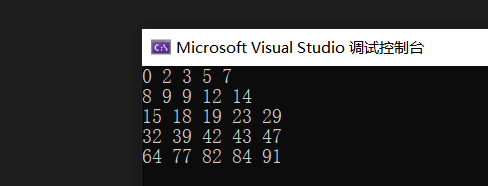
打印结果如下：

讲义P61-输入正整数n，打印集合的所有子集 

居然用到了位运算，是我掌握较为薄弱的一个方法。

对于数字0 ~ n-1而言，在一个子集每个数字有两种状态：存在和不存在，于是所有状态的组合就是所有的子集了，并且可知输入的正整数为n，子集的个数共有2 ^ n个。

根据上述，我们可以采用二进制数来代表所有的子集，1表示存在，0表示不存在。

例如输入3，则子集的总数为2^3 = 8个，集合为{0, 1, 2}。而二进制数也有8个，例如 001对应子集{2}，010对应子集{1}，011对应子集{1, 2}。

void powerset(int n)
{
    int m = pow(2, n);  //共有2^n种子集，对应2^n个二进制数
    int* subset = new int[n];   //记录子集
    int len;    //记录每次生成的子集的长度
    for (int i = 0; i < m; i++)     //大循环，遍历2^n个二进制数，确定2^n种子集
    {
        len = 0;
        for (int j = 0; j < n; j++) //遍历数字0 ~ n-1，检查每个数字是否存在于当前子集中
        {
            int tmp = 1 << j;       //将1左移j位，用tmp来检查第j个数字是否存在于当前子集中
            if (i & tmp)
            {
                subset[len++] = j;  //若存在则记录
            }
        }
        cout << "{";
        for (int j = 0; j < len; j++)
        {
            cout << subset[j];
            if (j < len - 1) cout << ", ";
        }
        cout << "}" << endl;
    }
}

int main()
{
    int n;
    cin >> n;
    powerset(n);
    return 0;
}

输出如下：

讲义P67-求所有元素个数为M的子集 

这道题用讲义上的位运算写法有点麻烦，可以直接用dfs来写。这里我直接让原集合中的元素都是1 ~ N - 1了。

int subset[100];
//N是集合中的元素个数，M表示要求元素个数为M的子集
//cur数组用于保存当前子集中的元素，len为cur数组中当前的元素个数
//index表示当前循环需要从下标为index的元素开始遍历
//每调用一次dfs函数，会确定当前子集中len位置的元素
void dfs(int cur[], int len, int M, int index, int N)
{
    //如果当前子集中的元素个数为M，打印
    if (len == M)
    {
        cout << "{";
        for (int i = 0; i < M; i++)
        {
            cout << cur[i];
            if (i < len - 1) cout << ", ";
        }
        cout << "}" << endl;
        return;
    }
    for (int i = index; i < N; i++)
    {
        cur[len] = subset[i];
        dfs(cur, len + 1, M, i + 1, N);
    }
}

int main()
{
    int N, M;    
    cin >> N >> M;
    for (int i = 0; i < N; i++)
    {
        subset[i] = i + 1;
    }
    int cur[100];    
    dfs(cur, 0, M, 0, N);
    return 0;
}

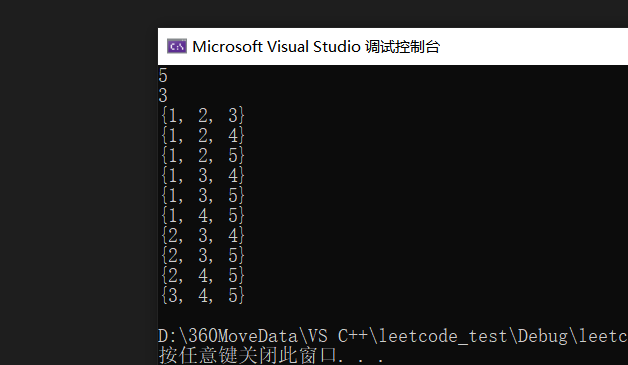
输出如下：

关于dfs函数中的遍历我原先写的是这样：

    for (int i = index; i < N; i++)
    {
        //选取
        cur[len] = subset[i];
        dfs(cur, len + 1, M, i + 1, N);
        //不选取
        dfs(cur, len, M, i + 1, N);
    }

对于cur[i]，分为选取和不选取两种情况，但是这样会导致相同的子集重复打印，例如集合{1,2,3}，如果按照上面这种写法，会重复打印子集{2,3}两次。

而下面这种正确的这种写法，其作用可以理解为每次调用dfs函数时，确定子集中len位置的元素，即每次确定cur[len]的值，这样一来可以保证在位置0~M - 1上，每个位置的元素不会重复出现

    for (int i = index; i < N; i++)
    {
        cur[len] = subset[i];
        dfs(cur, len + 1, M, i + 1, N);
    }

讲义P68-实现任意两个不同进制非负整数之间的转换

实现输入多组数据

这道题要求能够输入多组测试数据，先了解一下c++中如何输入多组数据：

int a;
string s;
while (cin >> a >> s)
{
    cout << a << " " << s << endl;
}

利用while循环和cin即可，只要输入的a是int型、s是string型，就能够不断循环、不断输入下去。但是如果输入的a不是int型，或者输入的s不是string型，while循环就会中断。

c语言中输入多组数据：

    int n;
    char ch;
    while (scanf_s("%d %c", &n, &ch) != EOF)
    {
        printf("%d %c\n", n, ch);
    }
    return 0;

while(scanf())按ctrl+z可退出循环，不过我用的vs中似乎while(scanf_s()) 得连按三次ctrl+z才行

另外这种输入方式不需要考虑是否会不小心将空格或回车读取进去，如果是以下这种输入方式就需要考虑用getchar()来消除多余的空格或回车了：

    char ch;
    while (1)
    {
        scanf("%c", &ch);
        getchar();
        if (ch == '*') break;
    }

本题代码

回到该题，实现代码如下：

int main()
{
    int a, b;
    string n;
    //多组的测试数据，将a进制的整数n转换为b进制
    while (cin >> a >> n >> b)
    {
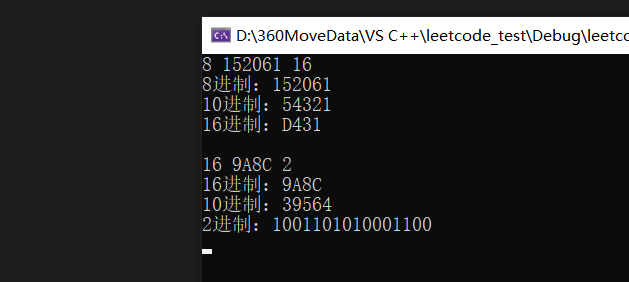
        cout << a << "进制：" << n << endl;
        int ten = 0;  //存储10进制数
        //先将a进制转换为10进制
        for (int i = 0; i <= n.size() - 1; i++)
        {
            int x = 0;  //记录该位数字
            if ('0' <= n[i] && n[i] <= '9')
            {
                x = n[i] - '0';
            }
            else if ('a' <= n[i] && n[i] <= 'z')
            {
                x = n[i] - 'a' + 10;
            }
            else if ('A' <= n[i] && n[i] <= 'Z')
            {
                x = n[i] - 'A' + 10;
            }
            ten = ten * a + x;  //这个地方就类似于10进制中的ten * 10 + x
        }
        cout << "10进制：" << ten << endl;
        //再将10进制转换为b进制
        string ans;
        while (ten > 0)
        {
            char ch;
            int x = ten % b;  //记录该位数字
            ch = x < 10 ? x + '0' : x - 10 + 'A';
            ans = ch + ans;
            ten /= b;
        }
        cout << b << "进制：" << ans << endl;
    }
    return 0;
}

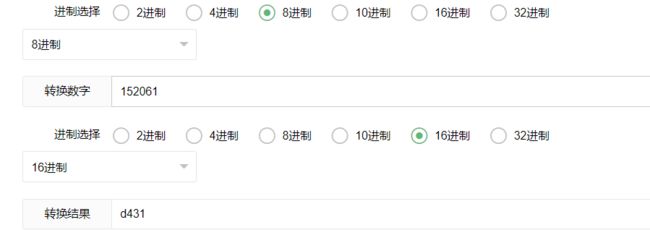
结果如下：

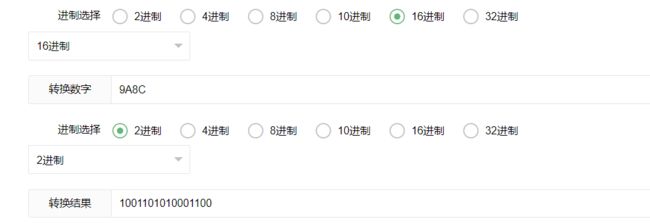
与网站上所给的结果相同：

讲义P80-交换两个向量的位置 

讲义P88-两个机器人的对话

不知道是不是原题就这样，这里描述了一下对话规则之后要没讲这题到底要我写什么。。

看了给的代码，才明白了这题是要对任意给出的一个字符串，判断是不是符合规则的对话内容

int main()
{
    string talk;
    cout << "请输入字符串：";
    cin >> talk;
    int n = talk.size();
    int i = 0;
    //while循环即为对话过程
    while(i < n)
    {
        //先由M1开始说话
        //当机器人说的不是数字时，必须继续说话
        while (i < n && (talk[i] == 'Y' || talk[i] == 'N')) i++;
        //当机器人说出数字时，自己必须停止说话，此时对方可以选择接着说话或停止对话
        if (i < n && talk[i] == '2') i++;
        //这里有两种情况：1、说的既不是2也不是Y或N  2、还没说出数字时对话就已经结束了
        else break;

        //接着由M2说话
        //当机器人说的不是数字时，必须继续说话
        while (i < n && (talk[i] == 'y' || talk[i] == 'n')) i++;
        //当机器人说出数字时，自己必须停止说话，此时对方可以选择接着说话或停止对话
        if (i < n && talk[i] == '1') i++;
        //这里有两种情况：1、说的既不是1也不是y或n  2、还没说出数字时对话就已经结束了
        else break;
    }
    if (talk[i - 1] == '1' || talk[i - 1] == '2')
    {
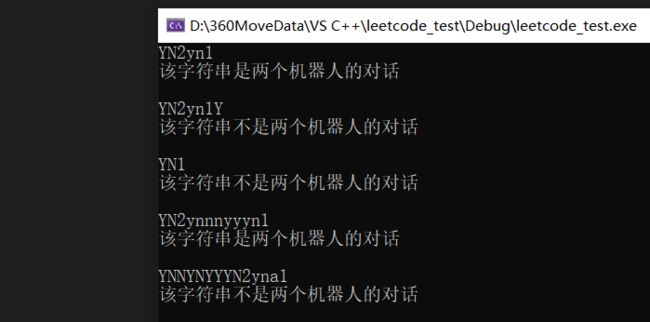
        if (i == n) cout << "该字符串是两个机器人的对话" << endl;
    }
    else cout << "该字符串不是两个机器人的对话" << endl;
    return 0;
}

结果如下： 

讲义P91-对n个字符串按字典序排序

字符数组的相关操作

这题居然限定了只能用字符数组，字符数组一直是我大一时较为薄弱的点，重新熟悉一下用法

    //字符数组的初始化，两种方式等价
    char str1[20] = { 'a', 'b', 'c', 'd', '\0' }; //注意其中每个字符是char类型的，最后需要手动添加'\0'
    char str2[20] = "abcd"; //可以自动添加'\0'

    char str3[20];
    scanf("%s", str3);
    printf("%s", str3);   //也可以直接 printf(str3)

    //字符串的赋值运算
    strcpy(str1, str2); //让str1 = str2

    //字符串的比较运算
    strcmp(str1, str2); //比较字典序，如果str1大于str2就返回正数，等于就返回0，小于就返回负数

    //字符串的拼接操作
    strcat(str1, str2); //将str2拼接到str1后面  //单词concat：合并多个字符串

    //求字符串的长度
    int len = strlen(str1);

注意 '\0' 是字符串结束的标志，例如以下代码将只打印ab

    char s[5] = { 'a', 'b', '\0', 'c' };
    printf("%s", s);

指针变量与变量指针 

① 字符串指针是一个指针变量，它可以指向任何字符串，可以把任意字符串首地址赋值给字符串指针。

② 字符数组名是一个指针常量，它只能表示分配给它的那块内存空间，不能让它指向其他字符串或数组，也不能用一个赋值运算把整个字符串赋值给一个字符数组。

【注】指针常量：

           格式为：数据类型  *   const  指针变量=变量名；

           表示指针是常量，即地址是常量，地址里存放的内容可以修改，但指针不能修改、不能作为左值

字符串指针和字符数组常见的各种用法举例：

    char str1[20] = "I Love You";   //正确，初始化字符数组

    char str2[20];
    str2 = str1;                    //错误，给指针常量赋值
    str2 = "I Love You";            //错误，给指针常量赋值
    str[] = "I Love You";           //错误，给指针常量赋值，"str[]"出现在"="左端，意义不明确
    scanf("%s", str2);              //正确，输入字符串

    char* str3;
    str3 = "I Love You";            //正确，给指针变量赋值，str3指向字符串常量
    scanf("%s", str3);              //错误，str3不指向任何变量，输入字符串无处存放

    str3 = str1; 
    scanf("%s", str3);              //正确，输入的字符串数据从str1[0]开始存放
    str3 = str1 + 5;                
    scanf("%s", str3);              //正确，输入的字符串数据从str1[5]开始存放

    int x = 1, y = 2;
    char str[]= "x = %d, y = %d\n";
    printf(str, x, y);              //正确，输出x = 1, y = 2（这个功能还挺有趣的）

本题代码

void Sort(char st[][10], int n)
{
    char tmp[10];
    //简单选择排序
    for (int i = 0; i < n; i++)
    {
        int mini = i;
        for (int j = i + 1; j < n; j++)
        {
            if (strcmp(st[j], st[mini]) < 0)
            {
                mini = j;
            }
        }
        if (mini != i)
        {
            strcpy_s(tmp, st[i]);
            strcpy_s(st[i], st[mini]);
            strcpy_s(st[mini], tmp);
        }
    }
}
int main()
{
    char st[5][10] = { "bcd", "f", "abc", "adc", "bcde" };
    Sort(st, 5);

    for (int i = 0; i < 5; i++)
    {
        printf("%s ", st[i]);
    }
    return 0;
}

输出如下：

讲义P92-将0元素移动到数组后面，非0元素保持有序

讲义P93-删除数组中值在x到y之间的所有元素

见过几次的题型，还是忘记了移动的操作了

//删除值在x到y之间的所有元素
int del(int A[], int n, int x, int y)
{
    int k = 0;  //记录当前被删除的元素的个数
    for (int i = 0; i < n; i++)
    {
        if (x <= A[i] && A[i] <= y)
        {
            k++;
        }
        else
        {
            A[i - k] = A[i];    //遇到非删除元素，就将其往前移动k个位置
        }
    }
    return n - k;   //返回删除后的元素个数
}

int main()
{
    int A[10] = { 21, 7, 6, 12, 1, 0, 5, 3, 4, 10 };
    int n = del(A, 10, 3, 7);   //删除3到7之间的所有元素
    for (int i = 0; i < n; i++)
    {
        cout << A[i] << " ";
    }
    return 0;
}

结果如下：

        

讲义P95-删除数组中值相同的元素

以往遇到这种问题直接用map，但是考研应该不能用这玩意吧，这题其实与上题大致相同，虽然我还是不会。

主要是第二层循环时要将所有与a[i]不相同的元素都向前移动，我原先想的是第二层循环碰到第一个与a[i]不相同的元素就移动然后直接退出循环了，但是这种想法是错的，例如{ 1, 2, 3, 3, 3, 4, 4, 5 }，若采用我原先的思路将3去重后变为{ 1, 2, 3, 4, 3, 4, 4, 5 }，那问题来了，第一层循环下一次的i指针应该指向哪里呢？这三个无论指向哪个都不行：{ 1, 2, 3, 4, 3, 4, 4, 5 }

PS：二刷时看错题目了，值相同的元素不一定连续，所以不能用上一题的方法。

//值相同的元素只保留一个，其他删除
int del(int a[], int n)
{
    int k;  //记录当前被删除的元素的个数
    //两层循环，第一层循环遍历数组中剩余的元素，第二层循环进行去重，并把其他元素向前移动
    for (int i = 0; i < n; i++)
    {
        int tmp = a[i];
        k = 0;  //每次要删除一个新的元素时都要重置一下删除的个数
        for (int j = i + 1; j < n; j++)
        {
            if (a[j] == tmp)
            {
                k++;
            }
            else a[j - k] = a[j];   //与a[i]不相同的元素往前移动k个位置
        }
        n -= k; //删除了k个元素，其他的元素都往前移动了k个位置，因此后面的几个位置上的元素没有意义，不用遍历
    }
    return n;   //返回删除后的元素个数
}

int main()
{
    int a[10] = { 1, 2, 3, 3, 3, 4, 5, 5, 6, 7 };
    int n = del(a, 10);
    for (int i = 0; i < n; i++)
    {
        cout << a[i] << " ";
    }
    return 0;
}

结果如下：

                

讲义P101-用数组精确计算M/N的各小数位的值

但凡与浮点数、小数位涉及上的问题，在我看来都是恶心。。

这题被输出结果整麻了，不过如果是手写代码的话就不用那么在意结果的严谨性了

int main()
{
    int M, N ;  //M为第一位被除数，N是除数
    cout << "请输入被除数：";
    cin >> M;
    cout << "请输入除数：";
    cin >> N;
    if (N > M)  //如果分子大于分母，先算出整数部分
    {
        cout << "整数部分：" << endl;
        cout << M / N << endl;
        M = M % N;
    }
    int a[100] = { 0 }; //存放商，即各位小数
    int b[100] = { 0 }; //存放余数
    int k = 0;  //小数个数
    int begin = 0, end = 0; //记录循环节的起止位置
    while (M != 0)  //当余数不为0时，说明除法运算还未结束，需要继续循环
    {
        a[k] = M * 10 / N;  //此次除法运算的商
        b[k] = M * 10 % N;  //此次除法运算的余数
        M = M * 10 % N;     //更新，M是此次除法运算的余数，也将作为下次除法运算的被除数
        //遍历余数数组，当余数出现重复时说明已经出现并完成了一次循环节
        for (int j = 0; j < k; j++) 
        {
            if (b[j] == M) 
            {
                begin = j + 1;  //循环节第一次出现的位置是第j + 1位，a[j]
                end = k;        //循环节结束的位置是第 k 位，a[k - 1]
                M = 0;          //设置跳出循环条件
                break;
            }
        }
        k++;
    }
    for (int i = 0; i < k; i++)
    {
        cout << a[i] << " ";
    }cout << endl;
    cout << "begin: " << begin << endl;
    cout << "end: " << end << endl;
    return 0;
}

示例：

讲义P105 生成螺旋矩阵

不太喜欢书上给的代码，通过找规律来做题有时候会给思考增加很大的负担，不如直接模拟螺旋矩阵的生成过程。

我采用了方向数组来控制在二维数组中的移动方向，因为赋值的方向就是右→下→左→上依次循环，每次沿着同个方向一直移动，直到坐标超出10*10或者碰到已经赋值过的位置，就改变方向

#define n 10
//方向数组
int dir[4][2] =
{
    {0, 1},     //右
    {1, 0},     //下
    {0, -1},    //左
    {-1, 0}     //上
};
int main()
{
    int num = 1;
    int a[10][10] = {0};
    int k = 0;  //方向数组的指针
    int i = 0, j = 0;   //起始坐标
    while (num <= n * n)  //从 1 打印到 n * n
    {
        a[i][j] = num;
        num++;
        int nexti = i + dir[k][0];
        int nextj = j + dir[k][1];
        //如果下一个坐标超出范围，或者下一个位置已经有数字了，就改变方向
        if (nexti < 0 || nexti >= 10 || nextj < 0 || nextj >= 10 || a[nexti][nextj] != 0)
        {
            k = (k + 1) % 4;
        }
        i = i + dir[k][0];
        j = j + dir[k][1];
    }

    for (int i = 0; i < 10; i++)
    {
        for (int j = 0; j < 10; j++)
        {
            printf("%4d", a[i][j]);
        }cout << endl << endl;
    }
    return 0;
}

以10*10矩阵为例：

讲义P106 二维数组排序

这题要注意，对于二维数组a，不能直接用*(a + i)来访问数组的第i个元素。

冒泡排序版

本来是想仿照外排序的那个归并排序的方法来写的，但是想了想实在有点麻烦，于是还是使用书上用指针来写冒泡的方法，确实十分简便。

#define n 5
void bubble_sort(int a[][n])
{
    //不能写int* p = a，因为a是int(*)[5]类型，只有当a为一维数组时可以这么写
    int* p = &a[0][0];    //等价于int* p = *a 或 int* p = a[0]
    for (int i = n * n - 1; i >= 0; i--)
    {
        bool flag = false;
        for (int j = 0; j < i; j++)
        {
            if (*(p + j) > *(p + j + 1))
            {
                int temp = *(p + j);
                *(p + j) = *(p + j + 1);
                *(p + j + 1) = temp;
                flag = true;
            }
        }
        if (!flag) break;
    }
}

int main()
{
    int a[n][n] =
    {
        {14, 9, 42, 9, 19},
        {39, 8, 2, 91, 43},
        {47, 84, 77, 12, 0},
        {23, 29, 7, 3, 5},
        {64, 32, 15, 18, 82}
    };
    bubble_sort(a);
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            cout << a[i][j] << " ";
        }cout << endl;
    }
    return 0;
}

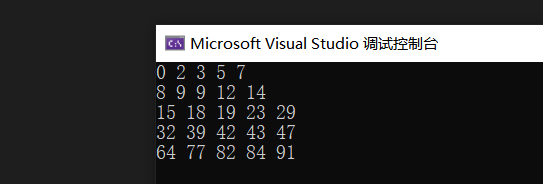
 结果：

插入排序版 

同样具有稳定性的插入排序也可以用此法写：

#define n 5
void insert_sort(int a[][n])
{
    //不能写int* p = a，因为a是int(*)[5]类型，只有当a为一维数组时可以这么写
    int* p = &a[0][0];    //等价于int* p = *a 或 int* p = a[0]
    for (int i = 0; i < n * n; i++)
    {
        int tmp = *(p + i);
        int j;
        for (j = i - 1; j >= 0 && *(p + j) > tmp; j--)
        {
            *(p + j + 1) = *(p + j);
        }
        *(p + j + 1) = tmp;
    }
}

int main()
{
    int a[n][n] =
    {
        {14, 9, 42, 9, 19},
        {39, 8, 2, 91, 43},
        {47, 84, 77, 12, 0},
        {23, 29, 7, 3, 5},
        {64, 32, 15, 18, 82}
    };
    insert_sort(a);
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            cout << a[i][j] << " ";
        }cout << endl;
    }
    return 0;
}

结果：

归并排序版

归并排序具有稳定性，也符合要求，虽然用归并排序写挺麻烦的，但用来练习练习

#define n 5
int b[n * n];
void merge(int a[][n], int low, int mid, int high)
{
    int i, j, k;
    //不能写int* p = a，因为a是int(*)[5]类型，只有当a为一维数组时可以这么写
    int* p = &a[0][0];    //等价于int* p = *a 或 int* p = a[0]
    for (int k = low; k <= high; k++)
    {
        b[k] = *(p + k);
    }
    for (i = low, j = mid + 1, k = low; i <= mid && j <= high; k++)
    {
        //是通过在b数组中比较，再把b数组中的数字转移到a数组中，不要搞混了
        if (b[i] <= b[j])
        {
            *(p + k) = b[i++];
        }
        else
        {
            *(p + k) = b[j++];
        }
    }
    while (i <= mid)
    {
        *(p + k) = b[i++];
        k++;
    }
    while (j <= high)
    {
        *(p + k) = b[j++];
        k++;
    }
}

void merge_sort(int a[][n], int low, int high)
{
    if (low < high)
    {
        int mid = (low + high) / 2;
        merge_sort(a, low, mid);
        merge_sort(a, mid + 1, high);
        merge(a, low, mid, high);
    }
}

int main()
{
    int a[n][n] =
    {
        {14, 9, 42, 9, 19},
        {39, 8, 2, 91, 43},
        {47, 84, 77, 12, 0},
        {23, 29, 7, 3, 5},
        {64, 32, 15, 18, 82}
    };
    merge_sort(a, 0, n * n - 1);
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            cout << a[i][j] << " ";
        }cout << endl;
    }
    return 0;
}

结果：

讲义P118-统计各个字符在字符串S中出现的次数

吉大似乎不让用string来写，有点懵。。之后还是改下习惯，用纯C来写代码好了。

使用数组作为函数参数、函数返回值的问题

在函数中传入a[]一般无法直接计算数组的大小（除非参数写的是int a[10]，但这种操作不常用），因为数组在函数中会退化成指针int*，因此无法用sizeof来计算，所以只能多传入一个参数记录原来的数组的大小。

int func(int a[], int n)
{
    //错误
    printf("%d", sizeof(a) / sizeof(int));

}

int main()
{
    int a[10];
    //正确
    printf("%d", sizeof(a) / sizeof(int));
    
    func(a, 10);
    return 0;
}

若要在函数中返回一个数组，因为C语言中不支持函数返回a[]这样的数组，所以需要转换成返回指针。

同时需要注意不能直接用int a[10] = {..}这样的方式创建数组然后返回，函数执行完之后这个数组就被释放掉了，会造成内存泄漏，所以还是需要动态申请空间。

另外如何才能知道返回的这个数组的大小呢？可以传入一个指针类型的参数来记录数组大小。

//用m来规定生成的数组的大小，用n返回生成的数组的大小
int* func(int m, int* n)
{
    int* a = (int*)malloc(m * sizeof(int));
    *n = m;
    for (int i = 0; i < m; i++)
    {
        //这里可以当成数组来使用，或者也可以用*(a + i) = i;
        a[i] = i;
    }
    return a;
}
int main()
{
    int m = 10;
    int n;
    int* a = func(m, &n);
    for (int i = 0; i < n; i++)
    {
        //可以当成数组来使用，或者也可以用printf("%d ", *(a + i));
        printf("%d ", a[i]);
    }
    free(a);
    return 0;
}

本题代码

int* func(char s[], char a[], int n)
{
    //动态申请n个int长的空间，记录a中每个字符在字符串s中出现的次数
    int* ans = (int*)malloc(n * sizeof(int));
    for (int i = 0; i < n; i++)
    {
        ans[i] = 0;
    }
    int sn = strlen(s);
    for (int i = 0; i < sn; i++)
    {
        for (int j = 0; j < n; j++)
        {
            if (s[i] == a[j]) ans[j]++;
        }
    }
    return ans;
}
int main()
{
    char s[10];
    scanf_s("%s", s, 10);
    char a[3] = { 'a', 'b', 'c' };
    int* ans = func(s, a, 3);
    for (int i = 0; i < 3; i++)
    {
        printf("%d ", ans[i]);
    }
    return 0;
}

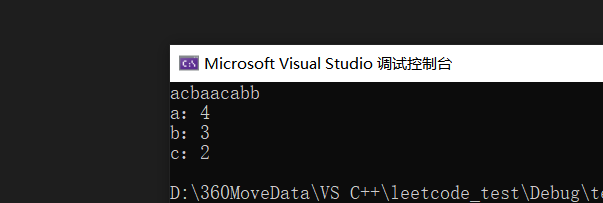
结果： 

讲义P121-输出s的值，精度1e-6

将整型赋值给浮点型的问题

下方例子中，右边的式子在运算前先看运算符两边变量的类型，然后再统一为同一类型进行运算，最后再将结果强制转换为左边的类型。

因此总结一下就是按照运算优先顺序，找到式子中最先运算的是哪些运算符，只要将这些运算符两边的变量强制转换为浮点型即可，这样接下来运算其他的运算符时就都转换为浮点类型的运算了。

    double a;

    a = 3 / 2;
    printf("%f\n", a);    //输出1.0

    a = 3.0 / 2;
    printf("%f\n", a);    //输出1.5

    a = 3.0 / 2 + 3 / 2;  //左边转换为了浮点型，而右边却没有转换
    printf("%f\n", a);    //输出2.5

    a = 3.0 / 2 + 3.0 / 2;//两边都转换为了浮点型
    printf("%f\n", a);    //输出3.0

    a = 3 / 2 * 2.0;      //强制转换不及时，在转换之前之前3 / 2就已经等于1了
    printf("%f\n", a);    //输出2.0

    a = 3.0 / 2 * 2;      //转换正确
    printf("%f\n", a);    //输出3.0

本题代码

题目所讲的精度没看懂，应该指的是类似泰勒公式中余项的精度吧？

int main()
{
    double s = 0;
    double t = 1;
    for (int n = 1; t > 1e-6; n++)
    {
        //例如 t = 1 / (2 * (double)n - 1) * 2 * n / (2 * n - 1)
        // 和  t = 1 / (2.0 * n - 1) * 2 * n / (2 * n - 1)
        // 和  t = 1 / (2 * n - 1.0) * 2 * n / (2 * n - 1)都行
        t = 1.0 / (2 * n - 1) * 2 * n / (2 * n - 1);
        s += t;
    }
    printf("%lf", s);


    return 0;
}

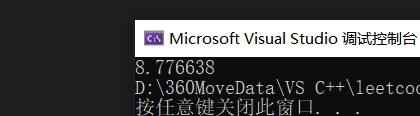
输出：

讲义P122-输出魔方阵

使用malloc动态创建二维数组

查了一下，有大概3种方法，这种应该是最好理解的也是最好记的一种了，先创建第一维，再创建第二维。

    int n;
    scanf_s("%d", &n);
    //动态创建二维数组
    int** a = (int**)malloc(sizeof(int*) * n);
    for (int i = 0; i < n; i++)
    {
        a[i] = (int*)malloc(sizeof(int) * n);
    }
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            a[i][j] = 0;
        }
    }

本题代码 

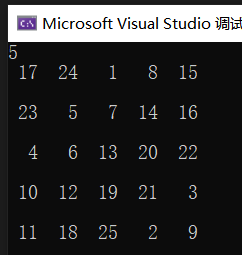
所谓的魔方阵就是指由1 ~ n*n的数组成的一个方阵，每一行、每一列和对角线之和均相等。该题所指的应该是奇数阶的魔方阵，因为偶数阶的需要另一种构造方法，与书中所给的不符。

奇数阶的魔方阵构造方法如下：

我觉得这种构造方法如果现想应该是没有多少人能想出来的。。

代码实现如下：

int main()
{
    int n;  //n为奇数
    scanf_s("%d", &n);
    //动态创建二维数组
    int** a = (int**)malloc(sizeof(int*) * n);
    for (int i = 0; i < n; i++)
    {
        a[i] = (int*)malloc(sizeof(int) * n);
    }
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            a[i][j] = 0;
        }
    }

    //i和j记录将要赋值的位置的行和列
    int i = 0;
    int j = n / 2;
    //首先，第一行的中间一列赋值为1
    a[i][j] = 1;
    for (int x = 2; x <= n * n; x++)
    {
        //新的行和列
        //这里注意，求newi和newj时不能用求余运算，因为-1 % n == -1
        int newi = i - 1 < 0 ? n - 1 : i - 1;
        int newj = j + 1 == n ? 0 : j + 1;
        if (a[newi][newj] != 0)
        {
            newi = i + 1 == n ? 0 : i + 1;
            newj = j;
        }
        i = newi;
        j = newj;
        a[i][j] = x;
    }
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            printf("%3d ", a[i][j]);
        }printf("\n\n");
    }
    return 0;
}

结果如下：

                          

讲义P127-计算调和级数的前n项和

所谓的调和级数：

 代码实现：

//辗转相除法
int gcd(int a, int b)
{
    return b == 0 ? a : gcd(b, a % b);
}

int main()
{
    for (int n = 1; n <= 10; n++)
    {
        int a = 1, b = 1;   //当前结果为a/b的分数形式
        //实际上已经有第1项1/1了，所以直接从第2项开始循环
        for (int i = 2; i <= n; i++)
        {
            //计算a/b + 1/i，先通分
            int newa = a * i + 1 * b;
            int newb = b * i;
            //再用辗转相除法计算分子和分母的最大公因数
            int tmp = gcd(newa, newb);
            a = newa / tmp;
            b = newb / tmp;
        }
        for (int i = 1; i < n; i++)
        {
            printf("1/%d + ", i);
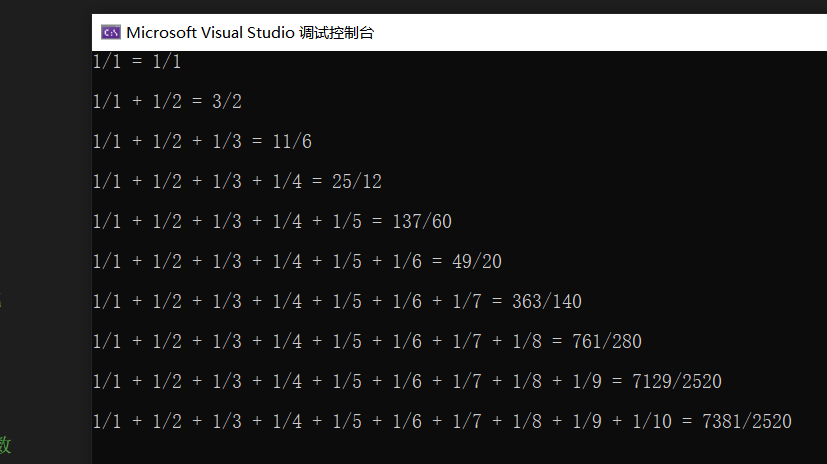
        }printf("1/%d = ", n);
        printf("%d/%d\n\n", a, b);
    }
    return 0;
}

结果：

讲义P130 && 讲义P136-计算sinx的近似值

这两页的写法不同，我比较喜欢后者，代码简洁易懂。

讲义P137-由小到大输出所有最简真分数

真分数是指大于0小于1的所有分数。这些分数的特点是“分母大于分子”。

找到符合条件的最简真分数，然后用直接插入法边插入边排序

struct fraction //表示分数 a/b
{
    int a;
    int b;
    double value;  //分数的值大小
};
int gcd(int a, int b)
{
    return b == 0 ? a : gcd(b, a % b);
}
int main()
{
    int n;
    scanf_s("%d", &n);
    struct fraction arr[100];
    int count = 0;  //找到的最简真分数的数量
    for (int i = 2; i <= n; i++)
    {
        for (int j = 1; j < i; j++)
        {
            if (gcd(i, j) == 1) //最大公因数为1，说明互质
            {
                fraction tmp;
                tmp.a = j;
                tmp.b = i;
                tmp.value = 1.0 * j / i;
                int k;
                for (k = count - 1; k >= 0 && arr[k].value > tmp.value; k--)    //直接插入法排序
                {
                    arr[k + 1] = arr[k];
                }
                arr[k + 1] = tmp;
                count++;
            }
        }
    }
    for (int i = 0; i < count; i++)
    {
        printf("%d/%d ", arr[i].a, arr[i].b);
    }
    return 0;
}

运行效果如下（题中所给的例子漏了一个1/3）： 

讲义P144-最大的三角形面积

这题需要先了解一下三角形面积如何用向量的叉乘来求。

讲义P146-寻找相切的圆

讲义P149-用二分法求方程的根

二分法

 

本题代码

#define eps 1e-6

double func(double x)   //计算函数值
{
    return 2 * pow(x, 3) - 4 * pow(x, 2) + 3 * x - 6;
}

int main()
{
    double left = -10, right = 10;
    if (func(left) * func(right) < 0)   //如果两端点的值同号的话，无法确定区域中是否有零点
    {
            double mid = (left + right) / 2;
            //注意，这题要求的精度是func(mid)值的大小，而不是区间的大小
            while (fabs(func(mid)) > eps)   //循环直到函数值在所给精度下接近于0
            {
                if (func(left) * func(mid) < 0) //说明零点存在于左区间
                {
                    right = mid;
                }
                else                            //否则说明零点存在于右区间
                {
                    left = mid;
                }
                mid = (left + right) / 2;
        }
    }
    printf("零点为：%lf", (left + right) / 2);
    return 0;
}

结果：

讲义P150-用牛顿迭代法求方程的根

牛顿迭代法

关于牛顿迭代法，参考此篇文章：(8条消息) 牛顿迭代法_江酱酱酱的博客-CSDN博客

本题代码

#define eps 1e-6

double func1(double x)   //计算函数值
{
    return 2 * pow(x, 3) - 4 * pow(x, 2) + 3 * x - 6;
}
double func2(double x)   //计算导数值
{
    return 6 * pow(x, 2) - 8 * x + 3;
}

int main()
{
    //x1是上一次的点，x2是最新一次的点
    double x1 = 1.5;
    double x2 = x1 - func1(x1) / func2(x1); //通过数学计算推导出来的值，是x1所对应的切线在x轴上的截距
    while (fabs(x1 - x2) > eps) //迭代直到两个点的距离足够小，小于所给精确度
    {
        x1 = x2;
        x2 = x2 - func1(x2) / func2(x2);
    }
    printf("零点是：%lf", x2);  //由于最后一次迭代x2的值还未赋给x1，因此更精确的零点值是x2
    return 0;
}

结果：

讲义P151-判断点是否在三角形内

用叉乘判断某点是否在三角形内

回忆一下高中知识，叉乘结果的方向可用右手定则来判断，因此当沿着三角形的边顺时针或逆时针方向走时，若要判断的点在三角形内，那三个叉乘的结果应该都是向上或者都是向下的；若该点在三角形边上，那么将会有一个叉乘的结果是0；若出现了不同的符号，就说明该点不在三角形内部了。

本题代码

#define eps 1e-6

typedef struct point    //点(x, y)
{
    double x, y;
}Point;
typedef struct vec      //向量
{
    double x, y;
}Vec;
//将两个点转换为向量
Vec turntovec(Point p1, Point p2)   
{
    Vec v;
    v.x = p1.x - p2.x;
    v.y = p1.y - p2.y;
    return v;
}
//计算两个向量的叉乘
double multivec(Vec v1, Vec v2)
{
    return v1.x * v2.y - v2.x * v1.y;
}
//判断浮点数x是否为0，若不为0则判断符号
int sign(double x)
{
    //当涉及判断浮点数是否为0时，要避免直接用==0来判断
    if (fabs(x) < eps) return 0;
    if (x > 0) return 1;
    return -1;
}

int main()
{
    Point ps[4];    //分别代表点A，B，C，D
    for (int i = 0; i < 4; i++)
    {
        scanf_s("%lf%lf", &ps[i].x, &ps[i].y);
    }
    Vec vs[3];
    //计算出三个向量DA, DB，DC
    for (int i = 0; i < 3; i++)
    {
        vs[i] = turntovec(ps[i], ps[3]);
    }
    int sgn[3]; //存储三个叉乘的符号
    //必须沿着三角形边的顺时针或逆时针方向进行叉乘，顺序不能乱
    //即只能计算DA×DB、DB×DC、DC×DA 或 DA×DC、DC×DB、DB×DA
    sgn[0] = sign(multivec(vs[0], vs[1]));
    sgn[1] = sign(multivec(vs[1], vs[2]));
    sgn[2] = sign(multivec(vs[2], vs[0]));
    
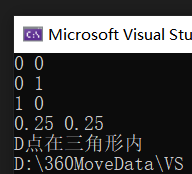
    if (sgn[0] == 0 || sgn[1] == 0 || sgn[0] == 0)  //若有某个叉乘的结果为0，说明D点与其中两个点位于一条直线上
    {
        printf("D点在三角形边上");
    }
    else if (sgn[0] == sgn[1] && sgn[1] == sgn[2])  //若三个叉乘的结果同号，说明D点在三角形内
    {
        printf("D点在三角形内");
    }
    else                                            //否则，说明D点在三角形外
    {
        printf("D点在三角形外");
    }
    return 0;
}

测试样例：

               

讲义P153-面积最大的多组三角形

这题书上所给的代码不严谨，它只能找到一个面积最大的三角形，而题目的条件是可能存在多组，因此要用一个数组存储搜寻过程中所找到的所有面积最大的三角形。

讲义P170-节点i经k步能到达的所有节点

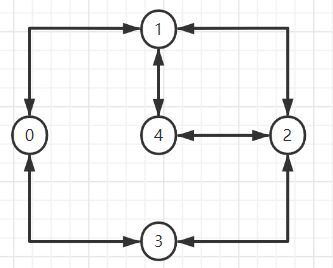
本题略坑，我以为节点是可以重复经过的，但按照所给的代码似乎不行。

以下图为例

代码实现：

#define n 5
//邻接矩阵
int a[n][n] =   
{
    {0, 1, 0, 1, 0},
    {1, 0, 1, 0, 1},
    {0, 1, 0, 1, 1},
    {1, 0, 1, 0, 0},
    {0, 1, 1, 0, 0}
};
int visit[n] = { 0 };   //判断某个节点是否被访问过
int ans[n] = { 0 };     //存储所能到达的所有节点
void dfs(int node, int path[], int k, int i)
{
    //标记到达过节点node，并将node加入路径
    visit[node] = 1;    //为什么要在这里标记节点呢？是为了能够在一开始将初始节点也顺便标记
    path[i] = node;     //同上，也是为了能够顺便将初始节点加入路径中
    if (i == k)
    {
        ans[node] = 1;
        for (int j = 0; j < k; j++)
        {
            printf("%d -> ", path[j]);
        }printf("%d\n", path[k]);
        return;
    }
    for (int j = 0; j < n; j++)
    {
        //如果存在node到节点j的路径
        if (a[node][j] == 1 && visit[j] == 0)
        {
            dfs(j, path, k, i + 1); //访问节点j
            visit[j] = 0;   //访问完节点j后将j再设为未访问
        }
    }
}
int main()
{
    int path[n] = { 0 };
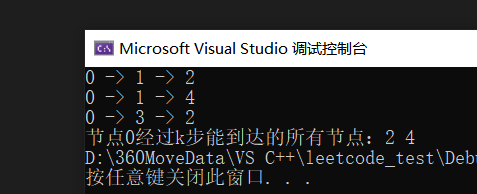
    dfs(0, path, 2, 0);
    printf("节点0经过k步能到达的所有节点：");
    for (int i = 0; i < n; i++)
    {
        if (ans[i] == 1)
        {
            printf("%d ", i);
        }
    }
    return 0;
}

示例：

                 

C语言文件操作

据说计专已经很多年不曾考过文件了，但是为了以防万一还是要做好准备，并且文件操作也是我的一个薄弱点，毕竟平时基本上都用不到，这方面参考吉大教材 P269 - P283，讲的还是很详细的。

讲义P173-用从文件中读取成绩信息，存入链表并排序

feof()函数多读一次的问题

在用while(!feof())判断文件是否到达末尾时，往往会多输出一组数据，在网上找了解释如下：

feof并不是返回当前的位置在不在文本末尾，而是返回当前位置后方还有没有内容。而在文本末尾系统会添加一个EOF标志来表示文本结束，所以当到EOF前时，明明应该停止读取，但因为当前位置后方还有内容（EOF也算内容），所以feof并不是马上返回非零值，而是下一次才返回非零值，这也就导致最后一次的结果会被打印两次。

例如对于下方代码：

    FILE* fp1 = fopen("file1.txt", "r+");

    char ch = ' ';
    while (!feof(fp1))
    {
        fscanf(fp1, "%c",&ch);
        printf("%c", ch);        //文本文件中内容为123，输出1233
    }

    fclose(fp1);

 解决这一问题可以采用如下的代码：

    FILE* fp1 = fopen("file1.txt", "r+");

    char ch = ' ';
    while (1)
    {
        fscanf(fp1, "%c",&ch);   //最后文件指针位于EOF标志前时，再读取一次就会时文件指针移到EOF标志后了
        if (feof(fp1)) break;  
        printf("%c", ch);        //文本文件内容为123，输出123
    }

    fclose(fp1);

但是采用这种写法还有个问题就是，使用fscanf读取数据时，如果格式是"%d"或"%s"，文本文件的最后一行必须多加一个回车，

例如如果文本文件是这样的话： 

那么对于代码：

    FILE* fp1 = fopen("file1.txt", "r+");

    printf("格式为%%d时的输出：\n");
    rewind(fp1);
    int x = 1;
    while (1)
    {
        fscanf(fp1, "%d", &x);
        if (feof(fp1)) break;
        printf("%d|", x);
    }printf("\n\n");

    printf("格式为%%s时的输出：\n");
    rewind(fp1);
    char s[10];
    while (1)
    {
        fscanf(fp1, "%s", &s);
        if (feof(fp1)) break;
        printf("%s|", s);
    }

    fclose(fp1);

那么上述的代码输出结果为：        

                                

当格式为%d和%s时都少输出了数据101，如果文本文件最后一行多加一个回车就不会有这样的问题。

总结：以后都使用第二种判断文件是否结束的方法，都在文本文件的末尾加个回车。

关于fscanf()读取数据时的问题

"%c"：一个字符一个字符地读取，也读取空格和换行符；

"%d"，"%s"：不读取空格和回车，遇到空格和回车则结束此次读取。（下方代码中由于是while循环，所以虽然没有读取空格和回车，但会继续读取后面的数据直到结束）

示例：

文本文件中的内容为：        

    FILE* fp1 = fopen("file1.txt", "r+");

    char ch = ' ';
    printf("格式为%%c时的输出：\n");
    while (1)
    {
        fscanf(fp1, "%c",&ch);
        if (feof(fp1)) break;
        printf("%c|", ch);
    }printf("\n\n");

    printf("格式为%%d时的输出：\n");
    rewind(fp1);
    int x = 1;
    while (1)
    {
        fscanf(fp1, "%d", &x);
        if (feof(fp1)) break;
        printf("%d|", x);
    }printf("\n\n");

    printf("格式为%%s时的输出：\n");
    rewind(fp1);
    char s[10];
    while (1)
    {
        fscanf(fp1, "%s", &s);
        if (feof(fp1)) break;
        printf("%s|", s);
    }

    fclose(fp1);

结果为：

                        

注意看，格式为%c时，7的前面和最后还有一行都有个|，这是因为fscanf读取了回车并输出

本题代码

原文本文件中内容：  

typedef struct student
{
    char stu_number[20];    //学号
    char name[20];          //姓名
    int discuss_score;      //讨论成绩
    int report_score;       //报告成绩
    int test_score;         //测试成绩
    float total_score;      //总成绩
    struct student* next;
}stu;
int main()
{
    FILE* fp = fopen("in.txt", "r");

    stu* head = (stu*)malloc(sizeof(stu));  //头节点
    head->next = NULL;
    while (1)
    {
        stu* temp = (stu*)malloc(sizeof(stu));
        temp->next = NULL;
        fscanf(fp, "%s %s %d %d %d", &temp->stu_number, &temp->name, &temp->discuss_score, &temp->report_score, &temp->test_score);
        if (feof(fp)) break;    //判断文件是否到达末尾
        //计算总成绩
        temp->total_score = 0.2 * temp->discuss_score + 0.2 * temp->report_score + 0.6 * temp->test_score;

        //插入排序
        stu* it1 = head;
        stu* it2 = head->next;
        for (it2 = head->next; it2 != NULL; it1 = it1->next, it2 = it2->next)
        {
            int cur = 0.2 * it2->discuss_score + 0.2 * it2->report_score + 0.6 * it2->test_score;
            //由于最终temp会插入*it1和*it2之间，而cur是*it2的总成绩，因此找到第一个总成绩小于temp的节点就退出
            if (temp->total_score >= cur)   //找到插入位置
            {
                break;
            }
        }
        it1->next = temp;
        temp->next = it2;
    }
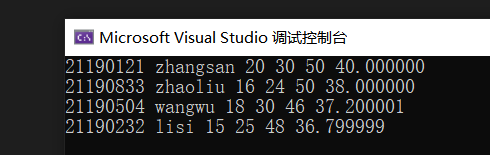
    for (stu* it = head->next; it != NULL; it = it->next)
    {
        printf("%s %s %d %d %d %lf\n", it->stu_number, it->name, it->discuss_score, it->report_score, it->test_score, it->total_score);
    }
    fclose(fp); //记得关闭文件，否则可能会是扣分点
    return 0;
}

输出结果(突然发现名字越长的分数越高hh)：

                

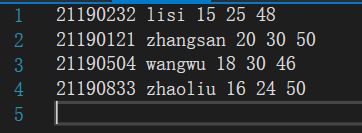
讲义P175-将学生信息存入链表，并写入文件中

/*
21190232 lisi 0 96
21190121 zhangsan 1 100
21190504 wangwu 1 97
21190833 zhaoliu 0 94
*/
typedef struct student
{
    char stu_number[20];    //学号
    char name[20];          //姓名
    int gender;             //性别，1为男，0为女
    int score;              //成绩
    struct student* next;
}stu;
stu* head = (stu*)malloc(sizeof(stu));

void CreatList(int n)
{
    for (int i = 0; i < n; i++)
    {
        stu* temp = (stu*)malloc(sizeof(stu));
        scanf("%s %s %d %d", temp->stu_number, temp->name, &temp->gender, &temp->score);
        temp->next = head->next;
        head->next = temp;
    }
}

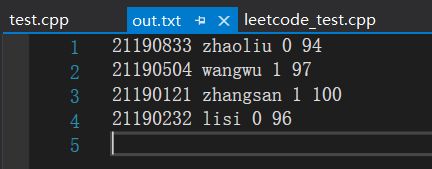
void WriteFile()
{
    FILE* fp = fopen("out.txt", "w");
    for (stu* it = head->next; it != NULL; it = it->next)
    {
        fprintf(fp, "%s %s %d %d\n", it->stu_number, it->name, it->gender, it->score);
    }
    fclose(fp);
}

int main()
{
    head->next = NULL;
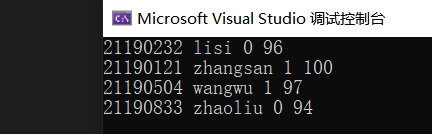
    CreatList(4);
    WriteFile();
    return 0;
}

写入信息：                

则结果为：

                                

讲义P177-冒泡法实现单向链表的排序

我的讲义上这面没了，自己实现了下发现还是有不少坑点的

#define maxsize 100
typedef struct no
{
    int val;
    struct no* next;
}node;
node* head = (node*)malloc(sizeof(node));
int main()
{
    int a[maxsize] = { 49, 38, 65, 97, 76, 13, 27, 49 };
    head->next = NULL;
    //创建链表
    for (int i = 0; i < 8; i++)
    {
        node* temp = (node*)malloc(sizeof(node));
        temp->val = a[i];
        temp->next = head->next;
        head->next = temp;
    }

    //冒泡排序
    int n = 0;
    for (node* it = head->next; it != NULL; it = it->next)
    {
        n++;    //先遍历计算节点的个数
    }
    //注意，外层循环不能用如下这条语句！因为发生节点交换后，it也不一定是原来的it了！
    //for (node* it = head->next; it != NULL; it = it->next)
    //i无实际意义，外层循环只需要用来计算遍历次数，因为每次冒泡确定一个数，那么至少需要n - 1次排序
    for (int i = 0; i < n - 1; i++)    //外层循环
    {
        int flag = 0;
        //需要用到三个指针first->second->third，排序时交换的是second和third指针，first指针用于辅助交换节点
        node* first = head, * second = first->next, * third = second->next;
        while (third != NULL)          //内层循环
        {
            //与普通的冒泡排序一样，只有在>时交换，可以保证稳定性
            if (second->val > third->val)
            {
                flag = 1;
                //下面三条语句发生节点交换，三个指针变为：first->third->second
                first->next = third;
                second->next = third->next;
                third->next = second;
            }
            //指针移动，发生节点交换和不发生交换时三个指针的先后顺序是不同的，不能随便交换
            //下面这种移动方式无论节点是否发生交换都适用
            first = first->next; //由于first指针一直是在第一位，因此可以先移动first指针
            second = first->next;//然后另外两个节点再依照first指针移动
            third = second->next;
        }
        if (!flag) break;   //与普通的冒泡排序相同，当不再发生交换时退出
    }//first->third->second

    for (node* it = head->next; it != NULL; it = it->next)
    {
        printf("%d ", it->val);
    }
    return 0;
}

注释中标注了自己所遇到的坑点，还有一个地方解释一下：

        //需要用到三个指针first->second->third，排序时交换的是second和third指针，first指针用于辅助交换节点
        node* first = head, * second = first->next, * third = second->next;

这里在赋值时不需要担心first和second为NULL会导致赋值出错，首先first初值赋为哨兵节点肯定不为NULL，而如果second为NULL则说明这个链表只有一个哨兵节点，n = 0，因此根本不会进入外层循环。

讲义P181-转换字符串并写入文件-练习4种文件读写方式

借用这题来练习一下文件读写的4种操作

    FILE* fpin = fopen("in.txt", "r");
    FILE* fpout = fopen("out.txt", "w");

    char str[20];
    //格式化读，注意"%s"的格式无法读取空格和回车，遇到就结束
    fscanf(fpin, "%s", str);

    //转换
    for (int i = 0; str[i] != '\0'; i++)
    {
        if ('a' <= str[i] && str[i] <= 'z')
        {
            str[i] = 'A' + (str[i] - 'a');
        }
    }
               
    //格式化写
    fprintf(fpout, "%s", str);

    fclose(fpin);
    fclose(fpout);

其中文件的读也可以采用以下方式：

    //字符读，可读取空格和回车
    int i = 0;
    char ch;
    while ((ch = fgetc(fpin)) != EOF)
    {
        str[i++] = ch;
    }
    str[i] = '\0';

    //字符串读，可读取空格，不能读取回车，因此每次最多能读取一行的所有内容
    //并且由于读取到的是字符串，所以可以自动添加'\0'
    fgets(str, 20, fpin);     

    //数据块读，这题其实不能用这种方式，因为读取之后没法加'\0'，无法完成后续的操作
    fread(str, sizeof(char), 20, fpin);

文件的写也可以采用以下方式：

    //字符写
    for (int i = 0; str[i] != '\0'; i++)
    {
        fputc(str[i], fpout);         
    }

    //字符串写
    fputs(str, fpout);                  

    //数据块写
    fwrite(str, sizeof(char), strlen(str), fpout);

讲义P183-将链表中的所有数字串到前面，所有字母串到后面

用scanf读取字符的问题

今天才知道原来scanf("%c")读取字符的时候会读入空格和回车，如下所示：

       ​​        

按下回车和空格后分别输出10和32,10就是换行符的ASCII码值，32是空格的ASCII码值。

因此如果在输入多个字符期间，按下了空格或回车的话会导致空格和回车被读入，想解决的话可以在scanf后加个getchar()，将缓冲区中的空格/回车读取走，但是getchar()也只能读取缓冲区中的一个字符，如果按了多个空格和回车还是治标不治本。

因此在使用scanf读入字符时还是尽量不要按空格和回车。

本题代码

这种分离链表的方法挺好的，也不用增加太多额外的空间。

typedef struct nodetype
{
    char ch;
    struct nodetype* next;
}node;
node* head = (node*)malloc(sizeof(node));   //原链表的哨兵节点
node* tail = head;                          //原链表的尾节点
int main()
{
    head->next = NULL;
    for (int i = 0; i < 10; i++)
    {
        node* temp = (node*)malloc(sizeof(node));
        scanf("%c", &temp->ch);
        temp->next = NULL;
        tail->next = temp;
        tail = temp;
    }
        
    node* num_head = (node*)malloc(sizeof(node));   //数字串的哨兵节点
    node* num_tail = num_head;                      //数字串的尾节点
    node* letter_head = (node*)malloc(sizeof(node));//字母串的哨兵节点
    node* letter_tail = letter_head;                //字母串的尾节点

    //遍历原链表，将数字节点添加到数字串中，将字母节点添加到字母串中
    for (node* it = head->next; it != NULL; it = it->next)
    {
        if ('0' <= it->ch && it->ch <= '9')
        {
            num_tail->next = it;
            num_tail = it;
        }
        else
        {
            letter_tail->next = it;
            letter_tail = it;
        }
    }
    //将数字串和字母串重新连接
    head->next = num_head->next;        //记得把原链表的哨兵节点指向新串
    num_tail->next = letter_head->next;
    letter_tail->next = NULL;

    for (node* it = head->next; it != NULL; it = it->next)
    {
        printf("%c ", it->ch);
    }

    return 0;
}

示例：

讲义P185-CCF会员信息排序

实现如下

typedef struct cardtype
{   
    int number;     //会员号，5位数字，最后一位数字若为偶数则代表高级会员，为奇数则代表低级会员
    char name[20];  //姓名
    int kind;       //0为高级会员，1为低级会员
    int day;        //有效期
    struct cardtype* next;
}card;
card* head = (card*)malloc(sizeof(card));

//使用冒泡排序
void sortcard()
{
    int n = 0;
    for (card* it = head->next; it != NULL; it = it->next)
    {
        n++;
    }
    for (int i = 0; i < n - 1; i++)
    {
        card* first = head, * second = first->next, * third = second->next;
        int flag = 0;
        while (third != NULL)
        {
            if (second->kind > third->kind)
            {
                flag = 1;
                first->next = third;
                second->next = third->next;
                third->next = second;
            }
            first = first->next;
            second = first->next;
            third = second->next;
        }
        if (!flag) break;
    }
}

int main()
{
    FILE* fp = fopen("in.txt", "r");

    head->next = NULL;
    while (1)
    {
        card* temp = (card*)malloc(sizeof(card));
        fscanf(fp, "%d %s %d", &temp->number, temp->name, &temp->day);
        if (feof(fp)) break;
        temp->kind = temp->number % 2;
        //插入排序，按照会员号从小到大排序
        card* it1, *it2;
        for (it1 = head, it2 = head->next; it2 != NULL; it1 = it1->next, it2 = it2->next)
        {
            if (it2->number > temp->number) break;
        }
        it1->next = temp;
        temp->next = it2;
    }

    printf("排序前：\n");
    for (card* it = head->next; it != NULL; it = it->next)
    {
        printf("%d %s %d %d\n", it->number, it->name, it->kind, it->day);
    }printf("\n");

    sortcard();

    printf("排序后：\n");
    for (card* it = head->next; it != NULL; it = it->next)
    {
        printf("%d %s %d %d\n", it->number, it->name, it->kind, it->day);
    }

    fclose(fp);
    return 0;
}

对于第三小题，只要使用能够保证稳定性的排序算法即可

示例：

                

讲义P191-创建学生信息链表，删除特定年龄的学生信息

/*
21190232 lisi 19
21190121 zhangsan 18
21190504 wangwu 21
21190833 zhaoliu 19
*/
typedef struct studenttype
{   
    int number;     //学号
    char name[20];  //姓名
    int age;        //年龄
    struct studenttype* next;
}student;
student* head = (student*)malloc(sizeof(student));
student* tail = head;

//删除所有年龄为z的节点
void deleteage()
{
    printf("要删除的年龄：");
    int z;
    scanf("%d", &z);
    student* it1 = head, * it2 = head->next;
    while (it2 != NULL)
    {
        if (it2->age == z)
        {
            it1->next = it2->next;
            it2 = it2->next;
        }
        else
        {
            it1 = it1->next;
            it2 = it2->next;
        }
    }
    //写入文件
    FILE* fp = fopen("out.txt", "w");
    for (student* it = head->next; it != NULL; it = it->next)
    {
        fprintf(fp, "%d %s %d\n", it->number, it->name, it->age);   
    }
    fclose(fp);
}

int main()
{
    int n = 4;
    head->next = NULL;
    for (int i = 0; i < n; i++)
    {
        student* temp = (student*)malloc(sizeof(student));
        scanf("%d %s %d", &temp->number, temp->name, &temp->age);
        temp->next = NULL;
        tail->next = temp;
        tail = temp;
    }printf("\n");

    printf("删除前：\n");
    for (student* it = head->next; it != NULL; it = it->next)
    {
        printf("%d %s %d\n", it->number, it->name, it->age);
    }printf("\n");

    deleteage(); printf("\n");

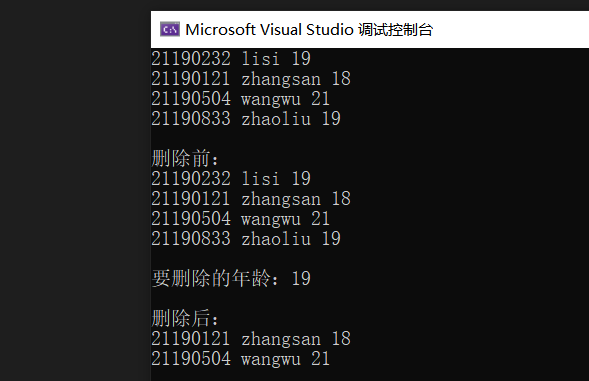
    printf("删除后：\n");
    for (student* it = head->next; it != NULL; it = it->next)
    {
        printf("%d %s %d\n", it->number, it->name, it->age);
    }

    return 0;
}

示例：

        

out.txt文件：

                                        

讲义P195-递归排序两个学生成绩链表

终于到了最后一题，递归排序我原以为是归并排序，原来是要求只要用递归实现的就行了，这里采用的是简单的插入排序的思想

/*
输入的内容：
21190232 lisi 94
21190121 zhangsan 100
21190504 wangwu 83
21190833 zhaoliu 88

文件in.txt中的内容：
21190125 qianqi 89
21190602 zhouba 95
21191127 sunjiu 78
21190919 zhengshi 91

*/
typedef struct studenttype
{   
    int number;     //学号
    char name[20];  //姓名
    int score;      //成绩
    struct studenttype* next;
}student;
student* head1 = (student*)malloc(sizeof(student)); //链表1的头节点
student* head2 = (student*)malloc(sizeof(student)); //链表2的头节点

//将链表2的节点按大小逐个插入到链表1中
//node1是链表1的节点，prenode1是node1的前驱节点，node2是链表2的节点
void sort_twolist(student* prenode1, student* node1, student* node2)
{
    //如果链表2已经遍历到结束，说明排序完毕
    if (node2 == NULL) return;
    //如果链表2还未结束，而链表1已经遍历到结束，则把链表2后续的节点都直接插入到prenode1的后面
    if (node1 == NULL)
    {
        prenode1->next = node2;
        return;
    }
    //如果node2的成绩比node1的成绩小，就把node2插入到prenode1和node1之间
    if (node1->score > node2->score)
    {
        student* reanode2 = node2->next;    //node2的后继节点
        prenode1->next = node2;
        node2->next = node1;
        //链表1变为prenode1->node2->node1
        //由于reanode2的成绩肯定大于等于node2的成绩，因此接下来比较reanode2和node1的成绩
        sort_twolist(node2, node1, reanode2);
    }
    //如果node2的成绩大于等于node1的成绩，就继续递归遍历链表1
    else
    {
        sort_twolist(node1, node1->next, node2);
    }
}

int main()
{
    head1->next = NULL;
    head2->next = NULL;
    int n = 4;
    for (int i = 0; i < n; i++)
    {
        student* temp = (student*)malloc(sizeof(student));
        scanf("%d %s %d", &temp->number, temp->name, &temp->score);
        //边插入边排序
        student* it1, * it2;
        for (it1 = head1, it2 = head1->next; it2 != NULL;it1 = it1->next, it2 = it2->next)
        {
            if (it2->score > temp->score) break;
        }
        it1->next = temp;
        temp->next = it2;
    }printf("\n");

    FILE* fp = fopen("in.txt", "r");
    while (1)
    {
        student* temp = (student*)malloc(sizeof(student));
        fscanf(fp, "%d %s %d", &temp->number, temp->name, &temp->score);
        if (feof(fp)) break;
        //边插入边排序
        student* it1, * it2;
        for (it1 = head2, it2 = head2->next; it2 != NULL; it1 = it1->next, it2 = it2->next)
        {
            if (it2->score > temp->score) break;
        }
        it1->next = temp;
        temp->next = it2;
    }printf("\n");


    printf("排序前：\n\n");
    printf("链表1：\n");
    for (student* it = head1->next; it != NULL; it = it->next)
    {
        printf("%d %s %d\n", it->number, it->name, it->score);
    }printf("\n");

    printf("链表2：\n");
    for (student* it = head2->next; it != NULL; it = it->next)
    {
        printf("%d %s %d\n", it->number, it->name, it->score);
    }printf("\n");

    sort_twolist(head1, head1->next, head2->next);  //调用递归排序函数

    printf("排序后：\n\n");
    for (student* it = head1->next; it != NULL; it = it->next)
    {
        printf("%d %s %d\n", it->number, it->name, it->score);
    }printf("\n");

    return 0;
}

 示例：

  

补充-用两个数组实现整数相乘

方法一

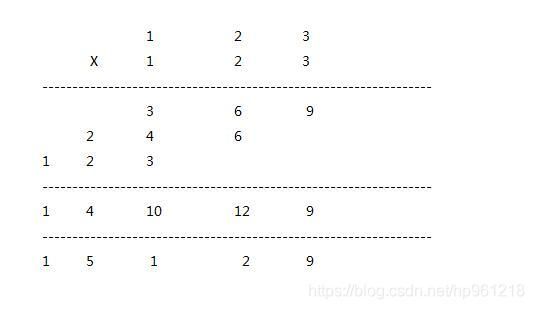
用一个数组表示一个正整数，一个数组元素表示整数的一位，例如396可以用数组a表示，即a[0] = 6, a[1] = 9, a[2] = 3，编一个函数，计算这样表示的两个整数a、b之积，积存放在数组c中。

这种数学问题就是模拟整数相乘的过程，思路倒是不难，但十分繁琐，考场上想要完整地写出来还是挺不容易的。

#define maxsize 100
//将一轮计算的结果加入c数组中，返回c数组的大小
int Add(int c[], int cur[], int curlen)
{
    int t = 0;  //存储上一次计算的进位
    for (int i = 0; i < curlen; i++)
    {
        int tmp = c[i] + cur[i] + t;  //每次计算时加上上一次的进位
        c[i] = tmp % 10;
        t = tmp / 10;                 //更新这一次计算的进位
    }
    if (t != 0) c[curlen++] = t;         //如果最后一次计算时还有进位，那么就将其作为最高位
    return curlen;
}

//a数组的大小n >= b数组的大小m
void multiply(int a[], int b[], int n, int m)
{
    int c[maxsize] = { 0 };
    int len = 0;
    int k = 0;          //标记第几轮
    int cur[maxsize];   //存储计算过程中每轮生成的数字
    int curlen = 0;     
    for (int i = 0; i < m; i++)     //对b数组从个位开始遍历
    {
        for (int j = 0; j < k; j++) cur[j] = 0;
        curlen = k;
        k++;
        int t = 0;  //存储上一次计算的进位
        for (int j = 0; j < n; j++) //对a数组从个位开始遍历
        {
            int tmp = b[i] * a[j] + t;  //每次计算时加上上一次的进位
            cur[curlen++] = tmp % 10;
            t = tmp / 10;               //更新这一次计算的进位
        }
        if (t != 0) cur[curlen++] = t;  //如果最后一次计算时还有进位，那么就将其作为最高位
        printf("第%d轮\n", k);
        printf("cur数组：");
        for (int j = curlen - 1; j >=  0; j--)
        {
            printf("%d ", cur[j]);
        }printf("\n");

        len = Add(c, cur, curlen);

        printf("c数组：");
        for (int j = len - 1; j >= 0; j--)
        {
            printf("%d ", c[j]);
        }printf("\n\n");
    }

    printf("最终结果：");
    for (int j = len - 1; j >= 0; j--)
    {
        printf("%d ", c[j]);
    }printf("\n\n");
}

int main()
{
    int a[maxsize] = { 6, 9, 3 };
    int b[maxsize] = { 2, 1 ,4, 5 };
    int n = 3, m = 4;
    multiply(b, a, m, n);
    
    return 0;
}

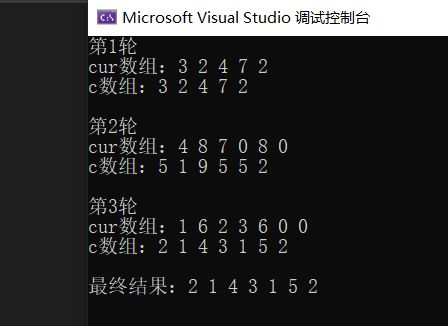
上述代码即模拟下方的计算过程：

                                  

 输出结果：

                        

方法二

答案的方法，真心nb

思路：

1、数组a的第i位和数组b的第j位的数字相乘，结果保存在数组c的第i+j位，但是注意i和j都必须是从0开始的，若从1开始则不能放在第i+j位（原理不太清楚，只能记下来吧）

2、对每一个数字进行进位

大概如下图所示：

                        

 代码：

#define maxsize 100

//a数组和b数组所代表的整数谁长谁短无所谓
void multiply(int a[], int b[], int n, int m)
{
    int c[maxsize] = { 0 };
    int len = 0;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            //数组a的第i位和数组b的第j位的数字相乘，结果保存在数组c的第i+j位
            c[i + j] += a[i] * b[j];
        }
    }
    for (int i = 0; i < maxsize; i++)
    {
        if (c[i] >= 10)     //若大于10则进位
        {
            c[i + 1] += c[i] / 10;  //进位
            c[i] %= 10;             //留下余数
        }
    }
    for (int i = 0; i < maxsize; i++)
    {
        if (c[i] != 0) len = i;     //寻找最后一个不为0的数字，即为最高位
    }
    printf("最终结果：");
    for (int i = len; i >= 0; i--)
    {
        printf("%d", c[i]);
    }
}

int main()
{
    int a[maxsize] = { 6, 9, 3 };
    int b[maxsize] = { 2, 1 ,4, 5 };
    int n = 3, m = 4;
    multiply(a, b, n, m);
    return 0;
}

上述代码的模拟过程为：

                        

输出结果：

                        

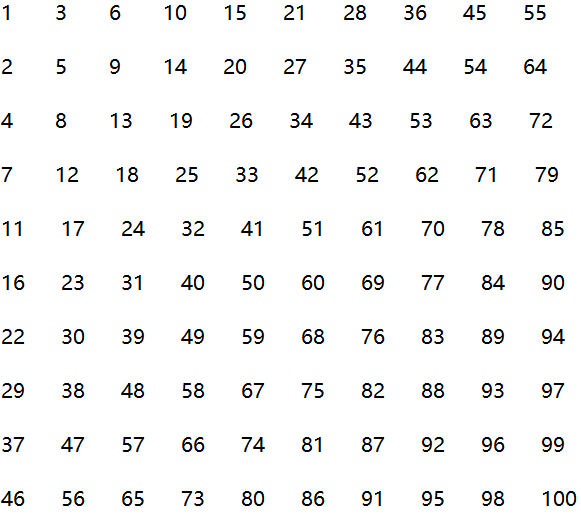
补充-打印特殊的二维数组

打印如下的二维数组：

                ​​​​​​​        ​​​​​​​        

int main()
{
    int a[10][10];
    int val = 1;
    //先打印上半矩阵，按斜线一条一条地向右打印
    for (int i = 0; i < 10; i++)
    {
        int x = i, y = 0;
        while (x >= 0 && y < 10)
        {
            a[x][y] = val++;
            x--;
            y++;
        }
    }
    //在打印下半矩阵，按斜线一条一条地向右打印
    for (int j = 1; j < 10; j++)
    {
        int x = 9, y = j;
        while (x >= 0 && y < 10)
        {
            a[x][y] = val++;
            x--;
            y++;
        }
    }

    for (int i = 0; i < 10; i++)
    {
        for (int j = 0; j < 10; j++)
        {
            printf("%d\t", a[i][j]);
        }printf("\n\n");
    }
    return 0;
}

打印结果如下：

补充-由二进制数字组成的环

挺有意思的题，我找到的规律虽然与答案不同，但程序貌似没毛病，思路如下：

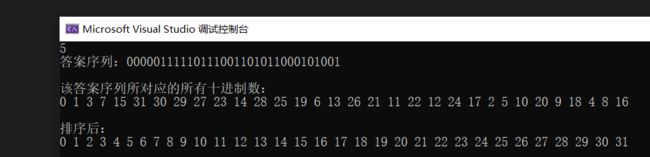
先将0所对应的二进制存入答案序列中，然后每次往后的一位二进制数优先选1，如果选择了1后所形成的新的十进制数已经被访问过，那就改成0，以此类推。

例如当n为3时，先存入000，然后下一位选择1，因为001所对应的十进制数1还未被访问过，因此不用改，答案序列更新为0001；以此类推，当答案序列为000111时，下一位选择1，但因为111所对应的十进制数3已经被访问过，因此改成0，答案序列更新为0001110。

代码如下：

#define maxsize 100

int main()
{
    int n;
    scanf("%d", &n);
    int len = pow(2, n);
    int visited[maxsize] = { 0 };   //标记某个数字是否被选中过
    int ans[maxsize];               //存储答案序列
    //一开始先将0所对应的二进制存入答案序列中
    for (int i = 0; i < n; i++) ans[i] = 0;
    visited[0] = 1;     //将 0 标记为已访问
    //因为已经存储了0所对应的二进制(即n-1个0)，所以答案序列的下一个数字从第n个位置开始存储
    for (int i = n; i < len; i++)
    {
        int tmp = 0;
        for (int j = i - n + 1; j < i; j++)
        {
            tmp = tmp * 2 + ans[j];
        }
        //如果答案序列的下一个数字选1，并且所对应的十进制数还未被访问过，就选1
        if (!visited[tmp * 2 + 1])
        {
            ans[i] = 1;
            visited[tmp * 2 + 1] = 1;
        }
        //否则选0
        else
        {
            ans[i] = 0;
            visited[tmp * 2 + 0] = 1;
        }
    }
    printf("答案序列：");
    for (int i = 0; i < len; i++)
    {
        printf("%d", ans[i]);
    }printf("\n\n");

    printf("该答案序列所对应的所有十进制数：\n");
    int a[maxsize];
    for (int i = 0; i < len; i++)
    {
        int tmp = 0;
        for (int j = 0; j < n; j++)
        {
            tmp = tmp * 2 + ans[(i + j) % len];
        }
        a[i] = tmp;
        printf("%d ", tmp);
    }printf("\n\n");

    printf("排序后：\n");
    for (int i = len - 1; i > 0; i--)
    {
        bool flag = false;
        for (int j = 0; j < i; j++)
        {
            if (a[j] > a[j + 1])
            {
                flag = true;
                int tmp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = tmp;
            }
        }
        if (!flag) break;
    }
    for (int i = 0; i < len; i++)
    {
        printf("%d ", a[i]);
    }printf("\n");
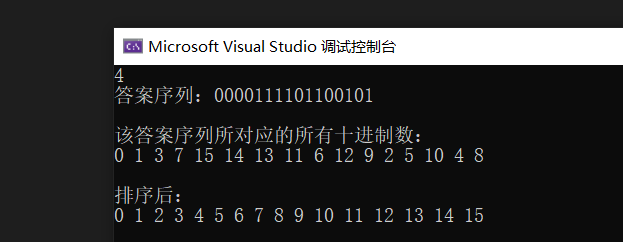
    return 0;
}

示例：

        ​​​​​​​        ​​​​​​​ 

         

 

补充-计算组合数

相关题目：119. 杨辉三角 II - 力扣（LeetCode）

在涉及到有关杨辉三角或二次项系数的题目时，都需要用到组合数，特此记录一下。

主要需要用到这么一个递推式：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​       

 这个递推式不难证明，不过通过杨辉三角来理解会更好记忆：

                

 忘记公式时，自己画个杨辉三角就能想起来了。

实现代码：

//计算组合数公式C(n, k)
int C(int n, int k)
{
    //对应C(0, 0)和C(n, n)的情况
    if (k == 0 || n == k) return 1;
    return C(n - 1, k - 1) + C(n - 1, k);

}
int main()
{
    int n, k;
    scanf("%d %d", &n, &k);
    printf("%d", C(n, k));
    return 0;
}

示例：

        ​​​​​​​    

补充-读取文件中的购物记录，计算购物总开销

2022软专最后两题，没难度，用来复习文件操作

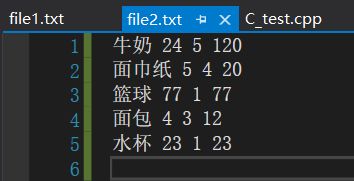
两个文件中的内容：

代码：

#define maxsize 100

typedef struct Shop
{
    char name[20];      //产品名称
    double price;       //单价
    int num;            //数量
    double totalprice;  //花费总额
    Shop* next;
}Shop;

Shop* creat(FILE* fp)
{
    Shop* head = (Shop*)malloc(sizeof(Shop));
    Shop* tail = head;
    while (1)
    {
        Shop* tmp = (Shop*)malloc(sizeof(Shop));
        fscanf(fp, "%s %lf %d %lf", tmp->name, &tmp->price, &tmp->num, &tmp->totalprice);
        if (feof(fp)) break;
        tail->next = tmp;
        tail = tmp;
    }
    tail->next = NULL;
    return head;
}

int main()
{
    FILE* fp1 = fopen("file1.txt", "r");
    FILE* fp2 = fopen("file2.txt", "r");
    Shop* head1 = creat(fp1);
    Shop* head2 = creat(fp2);
    double totalcost1 = 0, totalcost2 = 0;  //两个人的总开销
    printf("第一个人：\n");
    for (Shop* it = head1->next; it != NULL; it = it->next)
    {
        totalcost1 += it->totalprice;
        printf("%s\t%.1lf\t%d\t%.1lf\n", it->name, it->price, it->num, it->totalprice);
    }
    printf("总开销：%.1lf\n\n", totalcost1);
    printf("第二个人：\n");
    for (Shop* it = head2->next; it != NULL; it = it->next)
    {
        totalcost2 += it->totalprice;
        printf("%s\t%.1lf\t%d\t%.1lf\n", it->name, it->price, it->num, it->totalprice);
    }
    printf("总开销：%.1lf\n\n", totalcost2);
    printf("两个人的购物总开销的差值：%.1lf\n", fabs(totalcost1 - totalcost2));
    return 0;
}

 输出：