进化计算(五)——NSGA-II论文阅读笔记(二)
A fast and elitist multiobjective genetic algorithm NSGA-II阅读笔记(二)
- 测试函数
- 仿真
-
- 方法选择
- 初始参数设置
- 性能评价
- 结果
- 旋转多目标问题
- 约束处理—针对rank分配方法的改进
-
- 建议的约束处理方法——Constrained NSGA-II
- Ray–Tai–Seow的约束处理方法
- 对比结果
- Conclusion
- 参考链接
论文中展示了PAES、SPEA、NSGA II三个算法的对比实验结果。
测试函数
本篇论文采用的多目标优化测试函数为:SCH、FON、POL、KUR、ZDT1~ZDT4、ZDT6。ZDT问题集基本构建过程如下: m i n f 1 ( x ) m i n f 2 ( x ) = g ( x ) h ( f 1 ( x ) , g ( x ) ) minf_1(x)\\minf_2(x)=g(x)h(f_1(x),g(x)) minf1(x)minf2(x)=g(x)h(f1(x),g(x))更多关于ZDT问题的介绍参考该篇博客。
所有的测试函数都有两个目标函数 f 1 ( x ) , f 2 ( x ) f_1(x),f_2(x) f1(x),f2(x),且上述问题都没有约束条件。论文中的Table I给出了这些测试问题的决策变量个数、决策变量边界、Pareto最优解(Optimal solutions)以及Pareto前沿的性质(commet:凹凸、是否连续等)。
仿真
方法选择
二进制编码GA:单点交叉+按位变异;【进化计算(二)——简单的遗传算法编程(Matlab)代码中使用的就是单点交叉和按位变异的操作。】
对实数编码GA:模拟二进制交叉SBX算子+多项式变异;
初始参数设置
迭代次数:250;
交叉概率 p c = 0.9 p_c=0.9 pc=0.9;
变异概率 p m = 1 / n o r 1 / l p_m=1/n\quad or\quad1/l pm=1/nor1/l,其中 n n n是实数编码GA中决策变量的个数, l l l是二进制编码GA中字符串的长度;
实数编码:模拟二进制算子及多项式变异中分布指数取 η c = η m = 20 \eta _c=\eta _m=20 ηc=ηm=20;
性能评价
作者定义了两个指标 Υ \Upsilon Υ和 Δ \Delta Δ分别用于完成对收敛性和分布性的度量。
分布性 Υ \Upsilon Υ:从真实PF中选取500个等间隔分布的Pareto解,计算所获得的解与这500个解之间的最小欧式距离,这些距离的平均值即为 Υ \Upsilon Υ。 Υ \Upsilon Υ值越小,收敛性越好。
收敛性 Δ \Delta Δ:计算所获得的非支配解集中连续解之间的欧几里得距离 d i d_i di并取所有距离的平均值 d ˉ \bar{d} dˉ。首先通过拟合一个与PF平行的曲线计算极限解。然后使用下式计算分布的不均匀性:

其中, d f d_f df和 d l d_l dl是极限解与所获得的位于边界的分支配解之间的欧氏距离。 N N N是最优非支配前沿上解的个数。易判断, Δ \Delta Δ越小,分布性越好(当满足所有的 d i = d ˉ d_i=\bar{d} di=dˉ且 d f = d l = 0 d_f=d_l=0 df=dl=0时, Δ = 0 \Delta=0 Δ=0)。具体如下图所示:

结果
文章中的Table II和Table III展示了NSGA-II( Real-coded)、NSGA-II (Binary-coded)、SPEA、PAES四种算法的 Υ \Upsilon Υ和 Δ \Delta Δ对比结果(均值/方差)。
结果显示:
- 收敛性方面,除了ZDT3和ZDT6函数,NSGA-II算法表现的都比较好。在ZDT3和ZDT6函数上,采用固定存档策略的PAES算法表现得更好。
- 分布性方面:总体来看,两种NSGA-II算法在9个测试问题中表现的都比较好,分布性最差的是PAES算法。但在大部分问题中,实数编码的NSGA-II算法比二进制编码分布性能更好。
- 由于SPEA算法不能在最终种群中保留足够的非支配解,所以它在收敛性和分布性方面基本都比NSGA II性能差(除了在ZDT6函数上收敛性好)。
特别的,由于ZDT4函数有 2 1 9 21^9 219个不同的局部Pareto最优前沿,其中只有一个是全局Pareto最优前沿,所以在求解过程中很容易陷入局部最优。但从下图看出,NSGA-II算法虽然也陷入了局部最优,但其收敛性和分布性相对来说性能还是比较好的。
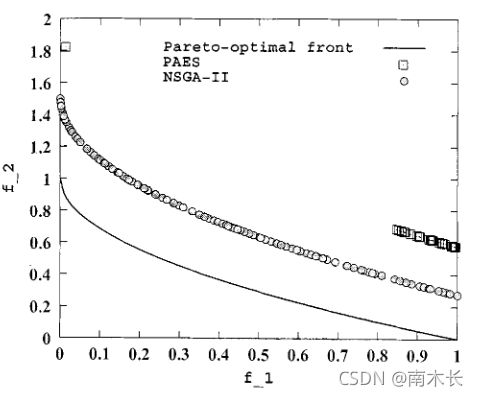
此外,作者还通过改变迭代次数等参数对结果进行了进一步解读:
- 将迭代次数由250改为500,其他参数保持不变:收敛性和分布性都得到了较多的改善。
- 改善ZDT4函数最优解的求解:保持其他参数不变,将实数编码NSGA-II中的 η m \eta _m ηm改为10:结果显示在 g ( x ) = 1 g(x)=1 g(x)=1时,NSGA-II在ZDT4函数上找到最优解:
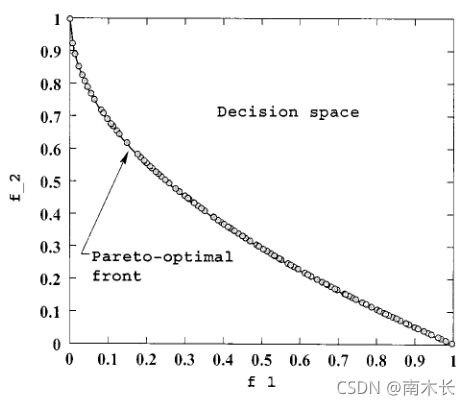
旋转多目标问题
参数交互会给多目标优化问题带来另一层面上的困难。针对上述三种算法,论文基于R1问题完成对旋转问题的讨论。
R1问题:

通常EA算法中决策向量为x,上述问题中的决策向量为x经旋转矩阵R变换的向量y。在这种方式下,目标函数就是一个线性组合的决策变量的函数。
测试时,采用SBX算子,迭代次数选500,种群规模选100。此外,为了满足 ∣ f 1 ∣ ≤ 0.3 |f_1|\le 0.3 ∣f1∣≤0.3,对在此范围外的的目标都附加一惩罚因子。结果显示,在该旋转问题中,NSGA-II表现性能更好。
约束处理—针对rank分配方法的改进
建议的约束处理方法——Constrained NSGA-II
该方法使用二进制锦标赛选择法,种群中的两个解更好的解被选中。在存在约束的情况下,可能有下边三种情况:①选出的两个解都是可行解;②其中一个解是可行解,另一个不是;③两个解都不是可行解。单目标优化可以用较简单的方法选中一个解:①选择目标函数值更好的解;②选择可行解;③选择约束冲突更小的解。
多目标优化中,②③两种情况限制处理同上。对于①,则可以使用拥挤比较算子解决。为了保证程序的模块化,作者对多目标优化问题下的支配关系进行了如下扩充定义。
D e f i n a t i o n : Defination: Defination:满足下列任一情况,可以说明解 i i i限制支配解 j j j。
- 解 i i i为可行解,解 j j j为不可行解;
- 两个解都不是可行解,但是解 i i i有更小的约束冲突。
- 两个解都是可行解,但是 i ≺ n j i \prec_nj i≺nj。
在这种支配关系下,所有的可行解拥有比任一不可行解更好的非支配排序等级。所有的可行解根据目标函数值获取非支配等级。对于两个不可行解,约束冲突值小的解被分配更好的非支配等级。该算法与Fonseca and Fleming的约束处理算法仅在不可行解之间的支配关系定义方面有所区别。
Ray–Tai–Seow的约束处理方法
该方法中对于所有约束条件的约束冲突并不简单求和,而是针对所有的约束冲突也进行非支配核对。虽然这种方法同时使用了目标函数值和约束冲突值,但是该方法无需任何惩罚因子。具体处理方法如下:
- 首先进行三种不同的种群非支配排序:
- 第一种排序使用 M M M个目标函数值,排序后的等级结果存放在 N N N维向量 R o b j R_{obj} Robj中;
- 第二种排序使用 J J J个约束冲突值,不使用目标函数信息,排序后的等级结果存放在向量 R c o n R_{con} Rcon中。易判断,所有的可行解约束冲突值为0,在 R c o n R_{con} Rcon中 r a n k = 1 rank=1 rank=1;
- 第三种排序使用 M M M个目标函数值和 J J J个约束冲突值,即 M + J M+J M+J个值,排序后的等级结果存放在向量 R c o m R_{com} Rcom中。
- 排序完成后, R c o m R_{com} Rcom中拥有更好等级的被下一代种群选中。如果种群还不满足种群规模大小,则遵循如下方案:在选择算子执行过程中偏重 R o b j R_{obj} Robj,在交叉算子执行过程中偏重 R c o n R_{con} Rcon。
该种算法可以解决一些工程问题,但是也引入了许多不同的算子,在解决更复杂问题时可能存在计算复杂度过高等问题。
对比结果
作者在四个限制约束问题CONSTR、SRN、TNK、WATER上进行proposed constraint-handling technique和Ray–Tai–Seow’s constraint-handling technique的对比仿真。针对四个问题,各自约束条件下的Pareto最优区域为:
- CONSTR:第一个约束边界和部分非约束Pareto最优区域的串联;
- SRN:非约束Pareto最优区域的子集;
- TNK:具有一个不连续的Pareto最优区域,完全落在第一个约束边界上;
- WATER:拥有五个目标函数和七个约束条件,难以说明约束条件下Pareto最优区域的形状。
仿真时,作者选取种群规模为100,迭代次数为500,实数编码中SBX和多项式变异中的分布参数分别选取20和100。
- 针对CONSTR问题,NSGA-II的收敛性和分布性都优于 Ray–Tai–Seow的算法。此外,为了保证分布性,所求得的解必须以一种依据约束函数的特殊方式进行修正。
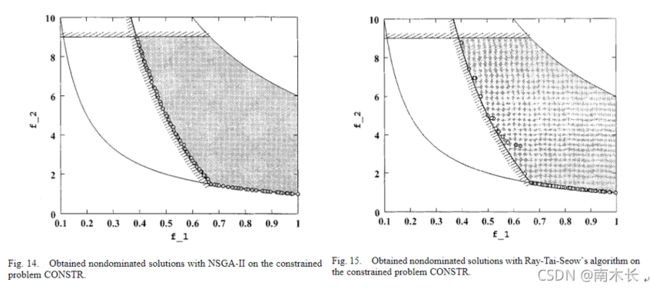
- 针对SRN问题,NSGA-II可以在PF上引入随机种群。两个算法的表现效果都很好。
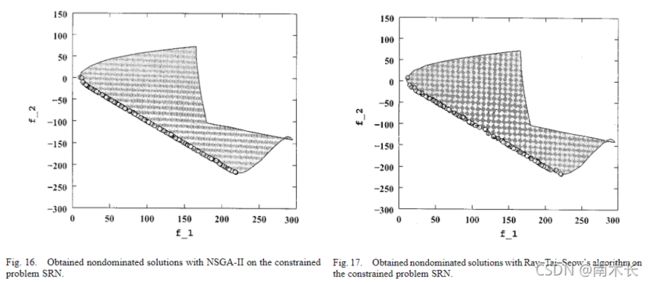
- 针对TNK问题,Pareto最优区域是不连续的。作者采用了proposed constraint-handling technique、Ray–Tai–Seow’s constraint-handling technique以及使用Fonseca–Fleming’s constraint-handling strategy的NSGA-II算法三种约束处理方法进行仿真,结果显示两种不同约束处理方法下的NSGA-II算法表现性能都较好而Ray–Tai–Seow算法性能较差且在所求解中出现了一些不可行解。

- 对于WATER函数,作者对十对( C 5 2 C_5^2 C52)函数组合分别进行求解,结果如下图所示。对于部分组合两种算法均不能实现很好的效果,但是对于部分函数组合(尤其是 f 1 − f 3 / f 1 − f 4 / f 3 − f 4 f_1-f_3/f_1-f_4/f_3-f_4 f1−f3/f1−f4/f3−f4组合),NSGA-II所求解很明显的接近PF。对比来说,NSGA-II算法性能还是较好的。

Conclusion
- 针对无约束NSGA-II算法,与PAES、SPEA算法相比,NSGA-II在9个测试问题上的收敛性和分布性更具优势。但是,PAES更能逼近真实PF。在搜索空间中,它通过控制在事先规定好的等大小cell中的解之间的拥挤度维持种群多样性。相较于NSGA-II和SPEA中使用的动态无参数拥挤方法,PAES中的这种算法更利于逼近真实PF。但是总体来说,NSGA-II分布性能最好。
- 针对旋转问题,NSGA-II更逼近真实PF,但是三个算法都存在高度上位性问题(非支配解集中分布在某些目标好但其他目标差的区域)。
- 针对约束处理问题,作者提出了一种基于NSGA-II算法的简单的限制多目标优化算法。实数编码NSGA-II算法在约束处理问题上性能更好。
参考链接
- 文献:A fast and elitist multiobjective genetic algorithm NSGA-II;
- 链接:实数编码;
- 博客1:ZDT问题介绍;
- 博客2:模拟二进制交叉;
- 博客3:多项式变异;
- 博客4:旋转多目标问题;