第七课 二叉堆、二叉搜索树
文章目录
- 第七课 二叉堆、二叉搜索树
-
- lc23.合并k个升序链表--困难
-
- 题目描述
- 代码展示
- lc239.滑动窗口最大值--困难
-
- 题目描述
- 代码展示
- lc355.设计推特--中等
-
- 题目描述
- 代码展示
- lc701.二叉搜索树中的插入操作--中等
-
- 题目描述
- 代码展示
- lc面试题0406.后继者--中等
-
- 题目描述
- 代码展示
- lc450.删除二叉搜索树中的节点--中等
-
- 题目描述
- 代码展示
- lc538.把二叉搜索转化为累加树--中等
-
- 题目描述
- 代码展示
第七课 二叉堆、二叉搜索树
lc23.合并k个升序链表–困难
题目描述
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2:
输入:lists = []
输出:[]
示例 3:
输入:lists = [[]]
输出:[]
提示:
k == lists.length0 <= k <= 10^40 <= lists[i].length <= 500-10^4 <= lists[i][j] <= 10^4lists[i]按 升序 排列lists[i].length的总和不超过10^4
代码展示
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
#includelc239.滑动窗口最大值–困难
题目描述
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 1041 <= k <= nums.length
代码展示
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> ans;
//双端队列,存放下标(代表时间)
deque<int> q;
for(int i= 0; i < nums.size(); i++){
//保证对头合法性
if(!q.empty() && q.front() <= i - k) q.pop_front();
//维护队列单调性,插入新的选项
while(!q.empty() && nums[q.back()] <= nums[i]) q.pop_back();
q.push_back(i);
//取队头更新答案
if(i >= k - 1) ans.push_back(nums[q.front()]);
}
return ans;
}
};
懒惰删除:
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> ans;
// pair<值,下标>
priority_queue<pair<int,int>> q;
for (int i = 0; i < k - 1; i++) q.push(make_pair(nums[i], i));
for (int i = k - 1; i < nums.size(); i++) {
q.push(make_pair(nums[i], i));
while (q.top().second <= i - k) q.pop(); // 懒惰删除,检查堆顶下标是否在窗口内
ans.push_back(q.top().first);
}
return ans;
}
};
// 懒惰删除
// 延迟到 当未删除的值 会影响答案时 再进行
// [1, 3, -1] priority_queue
// 正解:[3, -1, -3] max:3
// 懒惰删除:[1, 3, -1, -3] max:3
// 正解:[-1, -3, 5] max:5
// 懒惰删除:[1, 3, -1, -3, 5] max:5
// [-3 5 3] max:5
// 懒惰删除:[1, 3, -1, -3, 5, 3] max:5
// 如果是:1,3,-1,-3,2,3,6,7
// 正解:[3, -1, -3] max:3
// 懒惰删除:[1, 3, -1, -3] max:3
// 正解:[-1, -3, 2] max:2
// 二元组(值,下标)
// 懒惰删除:[(1, 0), (-1, 2), (-3, 3), (2, 4)] max:2
lc355.设计推特–中等
题目描述
设计一个简化版的推特(Twitter),可以让用户实现发送推文,关注/取消关注其他用户,能够看见关注人(包括自己)的最近 10 条推文。
实现 Twitter 类:
Twitter()初始化简易版推特对象void postTweet(int userId, int tweetId)根据给定的tweetId和userId创建一条新推文。每次调用此函数都会使用一个不同的tweetId。List检索当前用户新闻推送中最近getNewsFeed(int userId) 10条推文的 ID 。新闻推送中的每一项都必须是由用户关注的人或者是用户自己发布的推文。推文必须 按照时间顺序由最近到最远排序 。void follow(int followerId, int followeeId)ID 为followerId的用户开始关注 ID 为followeeId的用户。void unfollow(int followerId, int followeeId)ID 为followerId的用户不再关注 ID 为followeeId的用户。
示例:
输入
["Twitter", "postTweet", "getNewsFeed", "follow", "postTweet", "getNewsFeed", "unfollow", "getNewsFeed"]
[[], [1, 5], [1], [1, 2], [2, 6], [1], [1, 2], [1]]
输出
[null, null, [5], null, null, [6, 5], null, [5]]
解释
Twitter twitter = new Twitter();
twitter.postTweet(1, 5); // 用户 1 发送了一条新推文 (用户 id = 1, 推文 id = 5)
twitter.getNewsFeed(1); // 用户 1 的获取推文应当返回一个列表,其中包含一个 id 为 5 的推文
twitter.follow(1, 2); // 用户 1 关注了用户 2
twitter.postTweet(2, 6); // 用户 2 发送了一个新推文 (推文 id = 6)
twitter.getNewsFeed(1); // 用户 1 的获取推文应当返回一个列表,其中包含两个推文,id 分别为 -> [6, 5] 。推文 id 6 应当在推文 id 5 之前,因为它是在 5 之后发送的
twitter.unfollow(1, 2); // 用户 1 取消关注了用户 2
twitter.getNewsFeed(1); // 用户 1 获取推文应当返回一个列表,其中包含一个 id 为 5 的推文。因为用户 1 已经不再关注用户 2
提示:
1 <= userId, followerId, followeeId <= 5000 <= tweetId <= 104- 所有推特的 ID 都互不相同
postTweet、getNewsFeed、follow和unfollow方法最多调用3 * 104次
代码展示
class Twitter {
struct Node {
// 哈希表存储关注人的 Id
unordered_set<int> followee;
// 用链表存储 tweetId
list<int> tweet;
};
// getNewsFeed 检索的推文的上限以及 tweetId 的时间戳
int recentMax, time;
// tweetId 对应发送的时间
unordered_map<int, int> tweetTime;
// 每个用户存储的信息
unordered_map<int, Node> user;
public:
Twitter() {
time = 0;
recentMax = 10;
user.clear();
}
// 初始化
void init(int userId) {
user[userId].followee.clear();
user[userId].tweet.clear();
}
void postTweet(int userId, int tweetId) {
if (user.find(userId) == user.end()) {
init(userId);
}
// 达到限制,剔除链表末尾元素
if (user[userId].tweet.size() == recentMax) {
user[userId].tweet.pop_back();
}
user[userId].tweet.push_front(tweetId);
tweetTime[tweetId] = ++time;
}
vector<int> getNewsFeed(int userId) {
vector<int> ans; ans.clear();
for (list<int>::iterator it = user[userId].tweet.begin(); it != user[userId].tweet.end(); ++it) {
ans.emplace_back(*it);
}
for (int followeeId: user[userId].followee) {
if (followeeId == userId) continue; // 可能出现自己关注自己的情况
vector<int> res; res.clear();
list<int>::iterator it = user[followeeId].tweet.begin();
int i = 0;
// 线性归并
while (i < (int)ans.size() && it != user[followeeId].tweet.end()) {
if (tweetTime[(*it)] > tweetTime[ans[i]]) {
res.emplace_back(*it);
++it;
} else {
res.emplace_back(ans[i]);
++i;
}
// 已经找到这两个链表合起来后最近的 recentMax 条推文
if ((int)res.size() == recentMax) break;
}
for (; i < (int)ans.size() && (int)res.size() < recentMax; ++i) res.emplace_back(ans[i]);
for (; it != user[followeeId].tweet.end() && (int)res.size() < recentMax; ++it) res.emplace_back(*it);
ans.assign(res.begin(),res.end());
}
return ans;
}
void follow(int followerId, int followeeId) {
if (user.find(followerId) == user.end()) {
init(followerId);
}
if (user.find(followeeId) == user.end()) {
init(followeeId);
}
user[followerId].followee.insert(followeeId);
}
void unfollow(int followerId, int followeeId) {
user[followerId].followee.erase(followeeId);
}
};
/**
* Your Twitter object will be instantiated and called as such:
* Twitter* obj = new Twitter();
* obj->postTweet(userId,tweetId);
* vector param_2 = obj->getNewsFeed(userId);
* obj->follow(followerId,followeeId);
* obj->unfollow(followerId,followeeId);
*/
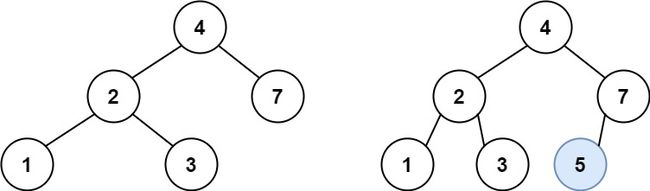
lc701.二叉搜索树中的插入操作–中等
题目描述
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:
输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
解释:另一个满足题目要求可以通过的树是:
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
提示:
- 树中的节点数将在
[0, 104]的范围内。 -108 <= Node.val <= 108- 所有值
Node.val是 独一无二 的。 -108 <= val <= 108- 保证
val在原始BST中不存在。
代码展示
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == nullptr) {
return new TreeNode(val);
}
TreeNode* pos = root;
while (pos != nullptr) {
if (val < pos->val) {
if (pos->left == nullptr) {
pos->left = new TreeNode(val);
break;
} else {
pos = pos->left;
}
} else {
if (pos->right == nullptr) {
pos->right = new TreeNode(val);
break;
} else {
pos = pos->right;
}
}
}
return root;
}
};
lc面试题0406.后继者–中等
题目描述
设计一个算法,找出二叉搜索树中指定节点的“下一个”节点(也即中序后继)。
如果指定节点没有对应的“下一个”节点,则返回null。
示例 1:
输入: root = [2,1,3], p = 1
2
/ \
1 3
输出: 2
示例 2:
输入: root = [5,3,6,2,4,null,null,1], p = 6
5
/ \
3 6
/ \
2 4
/
1
输出: null
代码展示
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public: //中序遍历
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
stack<TreeNode*> st;
TreeNode *prev = nullptr, *curr = root;
while (!st.empty() || curr != nullptr) {
while (curr != nullptr) {
st.emplace(curr);
curr = curr->left;
}
curr = st.top();
st.pop();
if (prev == p) {
return curr;
}
prev = curr;
curr = curr->right;
}
return nullptr;
}
};
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public: //利用二叉搜索树的性质
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
TreeNode *successor = nullptr;
if (p->right != nullptr) {
successor = p->right;
while (successor->left != nullptr) {
successor = successor->left;
}
return successor;
}
TreeNode *node = root;
while (node != nullptr) {
if (node->val > p->val) {
successor = node;
node = node->left;
} else {
node = node->right;
}
}
return successor;
}
};
lc450.删除二叉搜索树中的节点–中等
题目描述
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
- 节点数的范围
[0, 104]. -105 <= Node.val <= 105- 节点值唯一
root是合法的二叉搜索树-105 <= key <= 105
代码展示
class Solution {
public: //递归
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == nullptr) {
return nullptr;
}
if (root->val > key) {
root->left = deleteNode(root->left, key);
return root;
}
if (root->val < key) {
root->right = deleteNode(root->right, key);
return root;
}
if (root->val == key) {
if (!root->left && !root->right) {
return nullptr;
}
if (!root->right) {
return root->left;
}
if (!root->left) {
return root->right;
}
TreeNode *successor = root->right;
while (successor->left) {
successor = successor->left;
}
root->right = deleteNode(root->right, successor->val);
successor->right = root->right;
successor->left = root->left;
return successor;
}
return root;
}
};
class Solution {
public: //迭代
TreeNode* deleteNode(TreeNode* root, int key) {
TreeNode *cur = root, *curParent = nullptr;
while (cur && cur->val != key) {
curParent = cur;
if (cur->val > key) {
cur = cur->left;
} else {
cur = cur->right;
}
}
if (!cur) {
return root;
}
if (!cur->left && !cur->right) {
cur = nullptr;
} else if (!cur->right) {
cur = cur->left;
} else if (!cur->left) {
cur = cur->right;
} else {
TreeNode *successor = cur->right, *successorParent = cur;
while (successor->left) {
successorParent = successor;
successor = successor->left;
}
if (successorParent->val == cur->val) {
successorParent->right = successor->right;
} else {
successorParent->left = successor->right;
}
successor->right = cur->right;
successor->left = cur->left;
cur = successor;
}
if (!curParent) {
return cur;
} else {
if (curParent->left && curParent->left->val == key) {
curParent->left = cur;
} else {
curParent->right = cur;
}
return root;
}
}
};
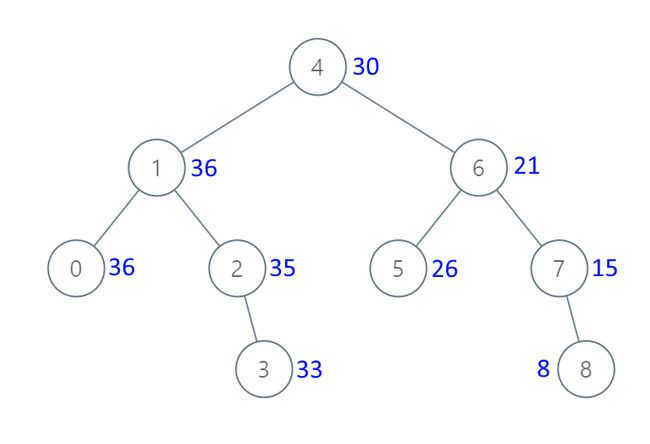
lc538.把二叉搜索转化为累加树–中等
题目描述
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
**注意:**本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同
示例 1:
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
示例 3:
输入:root = [1,0,2]
输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]
提示:
- 树中的节点数介于
0和104之间。 - 每个节点的值介于
-104和104之间。 - 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
代码展示
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public: //反序中序遍历
int sum = 0;
TreeNode* convertBST(TreeNode* root) {
if (root != nullptr) {
convertBST(root->right);
sum += root->val;
root->val = sum;
convertBST(root->left);
}
return root;
}
};