第十课 贪心
文章目录
- 第十课 贪心
-
- lc 322.零钱兑换--中等
-
- 题目描述
- 代码展示
- lc860.柠檬水找零--简单
-
- 题目描述
- 代码展示
- lc455.分发饼干--简单
-
- 题目描述
- 代码展示
- lc122.买卖股票的最佳时机II--中等
-
- 题目描述
- 代码展示
- lc45.跳跃游戏II--中等
-
- 题目描述
- 代码展示
- lc1665.完成所有任务的最少初始能量--困难
-
- 题目描述
- 代码展示
第十课 贪心
lc 322.零钱兑换–中等
题目描述
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
代码展示
class Solution {
public int coinChange(int[] coins, int amount) {
int INF = (int)1e9; // 定义一个无穷大的值,用于初始化 dp 数组
int[] opt = new int[amount + 1]; // 创建一个 dp 数组,用于存储凑成各个金额所需的最小硬币数量
opt[0] = 0; // 初始化金额为 0 时的硬币数量为 0
// 从金额 1 开始逐步计算到 amount
for (int i = 1; i <= amount; i++) {
opt[i] = INF; // 初始化为无穷大,表示无法凑成该金额
for (int j = 0; j < coins.length; j++) {
if (i - coins[j] >= 0) {
// 尝试使用每个硬币来凑成金额 i,并更新 dp[i] 的最小值
opt[i] = Math.min(opt[i], opt[i - coins[j]] + 1);
}
}
}
// 如果 opt[amount] 仍然等于 INF,表示无法凑成总金额,返回 -1;否则返回 opt[amount]
if (opt[amount] >= INF) {
opt[amount] = -1;
}
return opt[amount];
}
}
lc860.柠檬水找零–简单
题目描述
在柠檬水摊上,每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。
每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付 5 美元。
注意,一开始你手头没有任何零钱。
给你一个整数数组 bills ,其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零,返回 true ,否则返回 false 。
示例 1:
输入:bills = [5,5,5,10,20]
输出:true
解释:
前 3 位顾客那里,我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里,我们收取一张 10 美元的钞票,并返还 5 美元。
第 5 位顾客那里,我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零,所以我们输出 true。
示例 2:
输入:bills = [5,5,10,10,20]
输出:false
解释:
前 2 位顾客那里,我们按顺序收取 2 张 5 美元的钞票。
对于接下来的 2 位顾客,我们收取一张 10 美元的钞票,然后返还 5 美元。
对于最后一位顾客,我们无法退回 15 美元,因为我们现在只有两张 10 美元的钞票。
由于不是每位顾客都得到了正确的找零,所以答案是 false。
提示:
1 <= bills.length <= 105bills[i]不是5就是10或是20
代码展示
class Solution {
public boolean lemonadeChange(int[] bills) {
int fiveCount = 0;
int tenCount = 0;
for (int bill : bills) {
if (bill == 5) {
fiveCount++;
} else if (bill == 10) {
if (fiveCount > 0) {
fiveCount--;
tenCount++;
} else {
return false;
}
} else { // 当账单为20美元时
if (tenCount > 0 && fiveCount > 0) {
tenCount--;
fiveCount--;
} else if (fiveCount >= 3) {
fiveCount -= 3;
} else {
return false;
}
}
}
return true;
}
}
lc455.分发饼干–简单
题目描述
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。
示例 2:
输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.
提示:
1 <= g.length <= 3 * 1040 <= s.length <= 3 * 1041 <= g[i], s[j] <= 231 - 1
代码展示
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(), g.end());
sort(s.begin(), s.end());
int i = 0, j = 0;
int satisfied = 0;
while (i < g.size() && j < s.size()) {
if (s[j] >= g[i]) {
satisfied++;
i++;
}
j++;
}
return satisfied;
}
};
lc122.买卖股票的最佳时机II–中等
题目描述
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。
提示:
1 <= prices.length <= 3 * 1040 <= prices[i] <= 104
代码展示
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ans = 0; // 初始化最大利润为0
int n = prices.size(); // 获取股票价格数组的长度
for (int i = 1; i < n; ++i) { // 遍历股票价格数组
ans += max(0, prices[i] - prices[i - 1]); // 计算并累加利润,如果是负数则不累加
}
return ans; // 返回最大利润
}
};
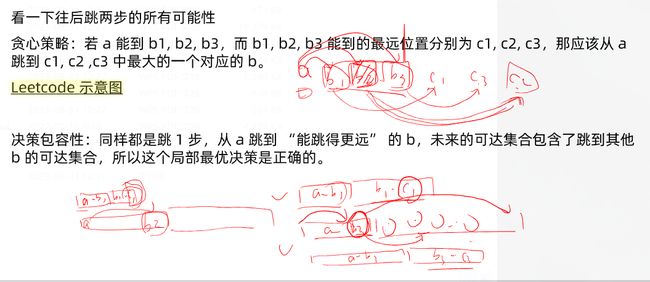
lc45.跳跃游戏II–中等
题目描述
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:
1 <= nums.length <= 1040 <= nums[i] <= 1000- 题目保证可以到达
nums[n-1]
代码展示
class Solution {
public:
int jump(vector<int>& nums) {
int n = nums.size();
int jumps = 0;
int farthest = 0;
int currentEnd = 0;
for (int i = 0; i < n - 1; i++) {
farthest = max(farthest, i + nums[i]); // 更新当前能够跳到的最远位置
if (i == currentEnd) { // 如果到达当前能够跳的最远位置
jumps++; // 增加跳跃次数
currentEnd = farthest; // 更新当前能够跳到的最远位置
}
}
return jumps;
}
};
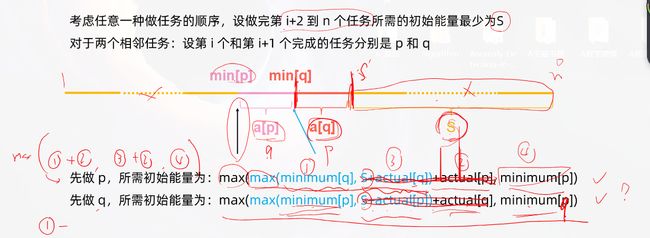
lc1665.完成所有任务的最少初始能量–困难
题目描述
给你一个任务数组 tasks ,其中 tasks[i] = [actuali, minimumi] :
actuali是完成第i个任务 需要耗费 的实际能量。minimumi是开始第i个任务前需要达到的最低能量。
比方说,如果任务为 [10, 12] 且你当前的能量为 11 ,那么你不能开始这个任务。如果你当前的能量为 13 ,你可以完成这个任务,且完成它后剩余能量为 3 。
你可以按照 任意顺序 完成任务。
请你返回完成所有任务的 最少 初始能量。
示例 1:
输入:tasks = [[1,2],[2,4],[4,8]]
输出:8
解释:
一开始有 8 能量,我们按照如下顺序完成任务:
- 完成第 3 个任务,剩余能量为 8 - 4 = 4 。
- 完成第 2 个任务,剩余能量为 4 - 2 = 2 。
- 完成第 1 个任务,剩余能量为 2 - 1 = 1 。
注意到尽管我们有能量剩余,但是如果一开始只有 7 能量是不能完成所有任务的,因为我们无法开始第 3 个任务。
示例 2:
输入:tasks = [[1,3],[2,4],[10,11],[10,12],[8,9]]
输出:32
解释:
一开始有 32 能量,我们按照如下顺序完成任务:
- 完成第 1 个任务,剩余能量为 32 - 1 = 31 。
- 完成第 2 个任务,剩余能量为 31 - 2 = 29 。
- 完成第 3 个任务,剩余能量为 29 - 10 = 19 。
- 完成第 4 个任务,剩余能量为 19 - 10 = 9 。
- 完成第 5 个任务,剩余能量为 9 - 8 = 1 。
示例 3:
输入:tasks = [[1,7],[2,8],[3,9],[4,10],[5,11],[6,12]]
输出:27
解释:
一开始有 27 能量,我们按照如下顺序完成任务:
- 完成第 5 个任务,剩余能量为 27 - 5 = 22 。
- 完成第 2 个任务,剩余能量为 22 - 2 = 20 。
- 完成第 3 个任务,剩余能量为 20 - 3 = 17 。
- 完成第 1 个任务,剩余能量为 17 - 1 = 16 。
- 完成第 4 个任务,剩余能量为 16 - 4 = 12 。
- 完成第 6 个任务,剩余能量为 12 - 6 = 6 。
提示:
1 <= tasks.length <= 1051 <= actuali <= minimumi <= 104
代码展示
class Solution {
public:
int minimumEffort(vector<vector<int>>& tasks) {
/*消耗(actual)小,门槛(minimum)大,是先做的条件
按actual + (-minimum)排序*/
sort(tasks.begin(), tasks.end(),
[](vector<int>& a, vector<int>& b) {
return a[0] - a[1] < b[0] - b[1];
});
// 正序做任务,但计算要倒序
int energy = 0; // 任务全部做完(什么也不用再做了)的时候,还需要0的能量
for (int i = tasks.size() - 1; i >= 0; i--) {
// minimum energy + actual
energy = max(tasks[i][1], energy + tasks[i][0]);
}
return energy;
}
};