数据拟合的相关函数(图像及应用实例 )- 基于python
数据拟合的相关函数(图像及应用实例 )- 基于python
本文提到的、的数学拟合需要基于numpy这个库,而为了将拟合更加直观的展示出来,用于绘图的matplotlib也是必要的,如果有想要跟着本文这些不值一提的思路去尝试实现的读者,需要预先安装这两个库。
本教程较为基础,因为笔者也是初学,只是做整理工作而已,因此在正式介绍拟合函数相关的内容之前有一些前置的会用到的函数说明,读者亦可跳过,直接前往拟合函数,有不熟悉的再往前翻阅亦可。
其他函数
numpy.linspace(start, end, number) & numpy.arange(start, end, step)
numpy.linspace这个函数可以生成相等间隔的数组(等差数列),几个参数分别是首项,尾项和项数,还有一些其他参数包括是否包括尾项、是否返回步长等等,可自行了解。
numpy.arange这个函数和numpy.linspace非常相像,前两个参数都是首项和尾项,只不过对于numpy.linspace来说,第三个参数是项数,而numpy.arrange的第三个系数是公差。另外numpy.linspace是默认包括尾项的,numpy.arange是默认不包括尾项的。
import numpy as np
print(np.linspace(1,5,5)) # [1,2,3,4,5]
print(np.arange(1,5,1)) # [1,2,3,4]
绘图函数
matplotlib.pyplot.scatter (x,y,c=None,marker =None)
作为一个绘图函数,matplotlib.pyplot.plot ()可以绘制散点图,这个函数有非常多的样式方面的自定义项,包括颜色、透明度、色彩映射等等,我们只选取颜色和散点形状讲解(大部分时候用于绘图时候的区分是足够了)
x和y是横纵坐标c是颜色,颜色可以用很多方式去声明,我们不需要颜色特别的精确,直接用特征字符串(‘red’ , ‘green’ 等)去声明就足够了marker是点的形状,常用的有(’o’ , ‘x’ , ‘+’ ,‘*’)他们的形状就像他们看到的那样
举例:简单散点图
import numpy as np
import matplotlib.pyplot as plt
x = [1, 2, 3, 4, 5]
y = [2, 2, 2, 2, 2]
plt.scatter(x, y, c='red', marker='x')
y = [1, 1, 1, 1, 1]
plt.scatter(x, y, c='green', marker='o')
plt.show()
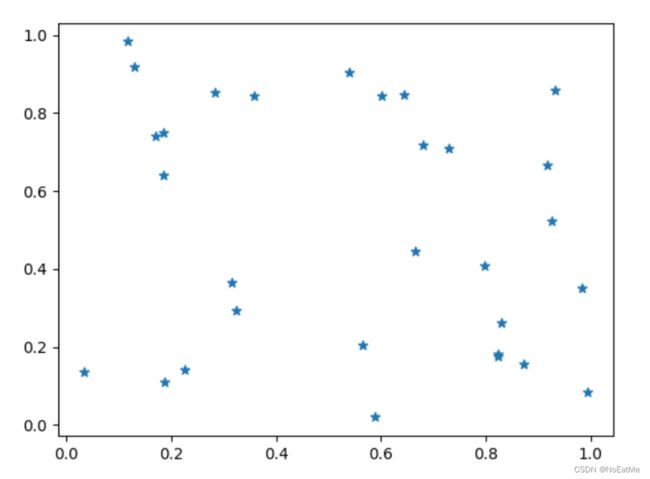
举例:随机散点图
也可以随机的生成一些散点
import numpy as np
import matplotlib.pyplot as plt
# 随机数组
x = np.random.rand(30)
y = np.random.rand(30)
plt.scatter(x,y,marker='*')
plt.show()
matplotlib.pyplot.plot ()
绘制折线图,只需要横纵坐标的值就可以画出折线图,本质是折线图了,因为是把点和点连在一起,但是只要点取得密集一点就可以了
例子 :不同描点密度的正弦函数
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0,3*np.pi,0.1)
y = np.sin(x)
x_2 = np.arange(0,3*np.pi,0.75)
y_2 = np.sin(x_2)
# 意思是把画板分成两行一列,这个子面板占据第一列
plt.subplot(2,1,1)
plt.plot(x,y,color = 'blue',label = 'step = 0.1')
plt.legend()
# 意思是把画板分成两行一列,这个子面板占据第二列
plt.subplot(2,1,2)
plt.plot(x_2,y_2,color = 'red',label = 'step = 0.75')
plt.legend()
plt.show()
拟合函数
numpy.polyfit (x, y, deg) -> List
该函数可以根据一组数据来拟合多项式曲线,其中
x和y是数据的横纵坐标,可以是任何以整形或浮点型为数据的可迭代对象,常用的有列表list和np.arraydeg是多项式次数
另有:
numpy.polyfit是基于最小二乘法的拟合
会返回一个列表,里面是符合deg的参数,如果是deg = 2,就返回三个系数(二次系数,一次系数,常数项),如果deg = 1,就返回两个系数(一次系数/斜率 , 常数项/截距)
numpy.poly1d(List)
numpy.poly1d()实际上是一个类的初始化:poly1d。概括来说,主要用于构建和操作多项式。最基础的语法为
import numpy as np
np.poly1d(coeff)
其中coeff是多项式系数列表,通过一个列表构建一个多项式对象,这个对象具有求值、求导、求积分、线性运算等多种工具,参考下列代码:
import numpy as np
coeff = [2,3,4]
p = np.poly1d(coeff) # 代表二次多项式 y = 2x^2 + 3x + 4
# 求值
print(p(3)) # 2 * 9 + 3 * 3 + 4 = 28
# 求导,返回新的多项式对象
x = p.deriv()
print(x) # 4 x + 3
# 积分
print(p.integ()) # 0.6667 x^3 + 1.5 x^2 + 4 x
# 支持多项式的加减乘除
print(p + p) # 4x^2 + 6x + 8
例子 :简单的直线拟合(一次项拟合)和曲线拟合(二次项拟合)
举例如下,最后图如下:
import numpy as np
import matplotlib.pyplot as plt
x = [1, 2, 3, 4, 5]
y = [1, 2, 3, 2, 1]
# 写成下面这样也是一样的,可以接受np.array形式
# x = np.array([1,2,3,4,5])
# y = np.array([1,2,3,2,1])
coeff = np.polyfit(x, y, 1) # 此例明显不适合用直线去拟合,但是要结果也是可以的
print(coeff) # [-0.42857143 2.57142857 -1.2] 分别为二次项系数,一次项系数和常数项
coeff2 = np.polyfit(x, y, 2)
print(coeff) # [5.98809768e-17 1.80000000e+00] 分别为一次项系数(斜率)和常数项(截距)
这也就是说,直线的拟合结果为(几乎就是 y = 1.8 y = 1.8 y=1.8)
y = 5.98809768 × 1 0 − 17 x + 1.8 y = 5.98809768\times 10^{-17}x + 1.8 y=5.98809768×10−17x+1.8
拟合的曲线是:
y = − 0.42857143 x 2 + 2.57142857 x − 1.2 y = -0.42857143x^2 + 2.57142857x -1.2 y=−0.42857143x2+2.57142857x−1.2
然后用numpy.poly1d()构建多项式,然后绘制散点图和线图
f = np.poly1d(coeff)
f2 = np.poly1d(coeff2)
# 从1到5,分成50格
n = np.linspace(1, 5, 50)
plt.scatter(x, y)
plt.plot(n, f2(n), color='red', label='y = ax^2 + bx + c')
plt.plot(n, f(n), color='green', label='y = kx + b')
plt.legend()
plt.show()
完整代码:
import numpy as np
import matplotlib.pyplot as plt
x = [1, 2, 3, 4, 5]
y = [1, 2, 3, 2, 1]
# 写成下面这样也是一样的,可以接受np.array形式
# x = np.array([1,2,3,4,5])
# y = np.array([1,2,3,2,1])
coeff = np.polyfit(x, y, 1) # 此例明显不适合用直线去拟合,但是要结果也是可以的
print(coeff) # [-0.42857143 2.57142857 -1.2] 分别为二次项系数,一次项系数和常数项
coeff2 = np.polyfit(x, y, 2)
print(coeff) # [5.98809768e-17 1.80000000e+00] 分别为一次项系数(斜率)和常数项(截距)
f = np.poly1d(coeff)
f2 = np.poly1d(coeff2)
# 从1到5,分成50格
n = np.linspace(1, 5, 50)
plt.scatter(x, y)
plt.plot(n, f2(n), color='red', label='y = ax^2 + bx + c')
plt.plot(n, f(n), color='green', label='y = kx + b')
plt.legend()
plt.show()
例子 : 通过拟合已知曲线+噪声的方式验证拟合的正确性
我们这一次预设一条曲线:
y = 4 x 2 + 3 x + 2 y = 4x^2+3x+2 y=4x2+3x+2
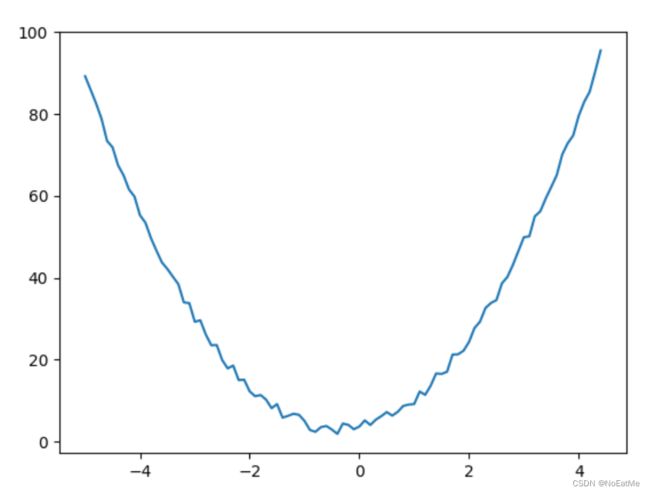
我们再这个基础上对每一个值加上一点随机的干扰,或者有些领域喜欢用噪声来描述。
大概的效果是这样:
之后我们再来对这组数据进行二次拟合,看看结果和我们预设的相差多少,完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-5,4.5,0.1)
y = 4*x**2 + 3*x + 2
# 加一点噪声
y = y + np.random.rand(len(x))*3
# 拟合
coeff = np.polyfit(x,y,2)
f = np.poly1d(coeff)
plt.plot(x,y)
plt.plot(x,f(x))
plt.show()
print(f"y = {coeff[0]}x^2 + {coeff[1]}x + {coeff[0]}")
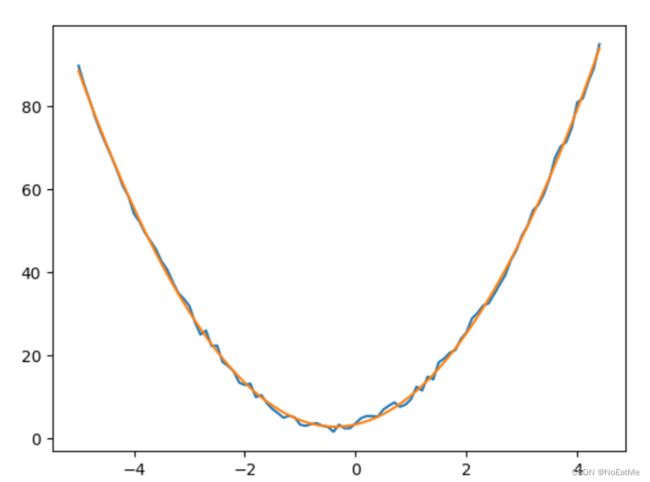
拟合曲线和原曲线对比:
最终结果:
| 二次项系数 | 一次项系数 | 常数项 | |
|---|---|---|---|
| 预设数据 | 4 | 3 | 2 |
| 拟合数据(取三位小数) | 4.002 | 2.980 | 4.002 |
| 误差(取两位小数) | 0.05% | 0.68% | 100.1% |
用polyfit去拟合一个高次多项式,越高次的系数拟合的越准,越低的系数乃至常数项误差越大,这是最小二乘方法的固有特性。
例子:其他形式的拟合(反比例,指数,对数等等)
有了上文的基础,其实面对一般的线性拟合,我们都能通过这种方法去模拟。
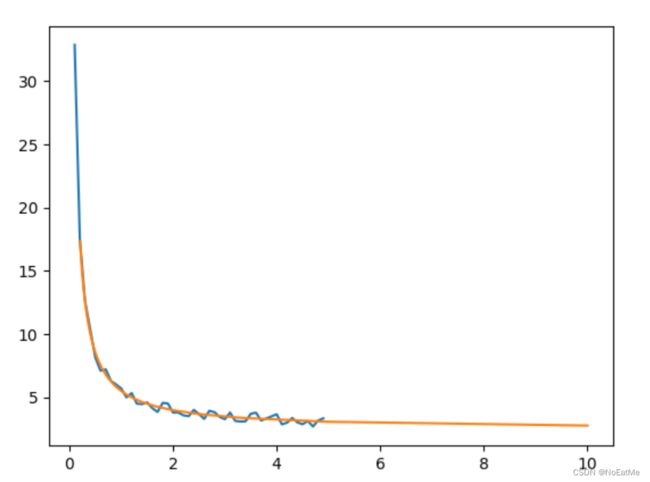
比如我们猜测两组数据之间有反比例关系:
y = k x + b y = \frac{k}{x} + b y=xk+b
我们可以可以直接令 x ′ = 1 x x' = \frac{1}{x} x′=x1,这样直接拟合 y y y和 x ′ x' x′之间的一次直线关系即可,完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
# 预设的原始数据
x = np.arange(0.1,5,0.1)
y = 3/x + 2
# 加一点噪声
y = y + np.random.rand(len(x))
# 拟合
coeff = np.polyfit(1/x,y,1)
f = np.poly1d(coeff)
plt.plot(x,y)
plt.plot(1/x,f(x))
plt.show()
print(f"y = {coeff[0]}/x + {coeff[1]}")
拟合的结果:
类似的,如果你怀疑有这样的关系:
y = k l n x + b y = klnx + b y=klnx+b
你可以直接令 x ′ = l n x x' = lnx x′=lnx,然后去拟合 y y y和 x ′ x' x′的一次关系。
或者你怀疑有这样的关系:
y = a x 2 + b x + c y = \frac{a}{x^2} + \frac{b}{x} +c y=x2a+xb+c
你可以直接令 x ′ = 1 x x' = \frac{1}{x} x′=x1,然后去拟合 y y y和 x ′ x' x′的二次关系。
凡此种种,不做赘述。