封装好的散点图拟合八大函数回归模型(逆、幂函、对数、S、复合、生长、指数 、线性函数,)
一.知识
给定一些散点,拟合函数去分析其自变量和因变量变动关系,这时候可以选择多种函数去进行拟合
例如excel里面会有添加趋势线这种工具,里面可以选择不同的工具,spss里面有不同函数可以同时选择进行拟合。
但是以上两种方法对单组数据操作比较方便,如果有多组数据就要不停重复导入数据进行操作,查看趋势线,该工作过于繁杂,所以创建了该代码。该函数我已经封装好代码欢迎直接调用我的代码。
二、代码调用过程
我已经虚拟一套数据集作为列子
| 日期 | 标签 | 自变量 | 因变量 |
| 2021年1月1日 | A | 49.63594 | 5.540451 |
| 2021年1月2日 | A | 24.5104 | 5.234005 |
| 2021年1月3日 | A | 49.93535 | 5.543063 |
| 2021年1月4日 | A | 62.09605 | 5.637719 |
| 2021年1月5日 | A | 82.77789 | 5.762569 |
| 2021年1月6日 | A | 88.63828 | 5.792276 |
| 2021年1月7日 | A | 6.045908 | 4.626116 |
| 2021年1月8日 | A | 7.498912 | 4.719653 |
| 2021年1月9日 | A | 9.502011 | 4.82247 |
| 2021年1月10日 | A | 60.30125 | 5.624981 |
| 2021年1月11日 | A | 45.19309 | 5.499727 |
| 2021年1月12日 | A | 5.901614 | 4.615626 |
| 2021年1月13日 | B | 41.6386 | 135.8847 |
| 2021年1月14日 | B | 58.23258 | 188.4683 |
| 2021年1月15日 | B | 15.78591 | 52.23334 |
| 2021年1月16日 | B | 32.88107 | 108.2983 |
| 2021年1月17日 | B | 68.40336 | 219.6259 |
| 2021年1月18日 | B | 22.22 | 72.62345 |
| 2021年1月19日 | B | 8.048647 | 29.02982 |
| 2021年1月20日 | B | 33.13403 | 106.557 |
| 2021年1月21日 | B | 86.59669 | 277.6387 |
| 2021年1月22日 | B | 94.47097 | 304.685 |
| 2021年1月23日 | B | 57.93375 | 186.9587 |
| 2021年1月24日 | B | 30.49006 | 99.87595 |
| 2021年1月25日 | C | 25.24164 | 18.41345 |
| 2021年1月26日 | C | 38.64638 | 63.9966 |
| 2021年1月27日 | C | 18.45192 | 65.63098 |
| 2021年1月28日 | C | 84.22761 | 268.1763 |
| 2021年1月29日 | C | 23.32117 | 61.23712 |
| 2021年1月30日 | C | 97.17947 | 237.9303 |
| 2021年1月31日 | C | 48.25496 | 40.07267 |
| 2021年2月1日 | C | 16.88487 | 29.8532 |
| 2021年2月2日 | C | 24.10362 | 28.57303 |
| 2021年2月3日 | C | 61.63955 | 107.2201 |
| 2021年2月4日 | C | 72.30827 | 215.4583 |
| 2021年2月5日 | C | 81.15836 | 239.947 |
这里开始讲解我的参数
data_df:导入的dataframe列名如下,['日期',‘标签’,‘自变量’,‘因变量’],日期这一列名称可以进行自定义,可以不按照我的,设置自己喜欢的index方式,其他三列请按照我的名称。ps:标签是记录哪一组数据回归的意思。测试的数据集,我会放入我的资源里面,欢迎大家下载测试代码。
x_自变量: x_自变量='自变量' ,这里输入自变量的名称。
y_因变量: y_因变量='因变量' ,这里输入你变量的名称。
fw:np.arange(1,100,1) ,这里numpy生产一系列数据,这里控制的是x轴的范围,怎么画图。
io_1:r'C:\Users\***\Desktop\临时文件',这个写入生成的回归图片保存的路径
def analysis_of_regression(data_df,x_自变量,y_因变量,fw,io_1):
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.metrics import r2_score
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
#%%需要外部加载的变量
# df_a = pd.DataFrame( columns=['标签','类型', 'r2', '航司','公式'])
df_a = pd.DataFrame()
df_d = pd.DataFrame(columns=('标签','类型','r2','系数'))
data_array = np.array(data_df[['标签']])
b=data_array.tolist()
a=[x for tup in b for x in tup]
a = list(set(a))
#开始进行函数拟合
for i in a:
# for i in [1]:
jj=data_df[(data_df['标签']==i)]
# jj=data_df
##线性
x_cz_2=jj[['自变量']].values.tolist()
y_cz_2=jj[['因变量']].values.tolist()
x_cz_2=sum(x_cz_2,[])
y_cz_2=sum(y_cz_2,[])
L=np.polyfit(x_cz_2, y_cz_2, 1)
print(L)
Z=np.polyval(L,x_cz_2,)
score = r2_score(y_cz_2, Z, multioutput='raw_values')
print('线性:'+str(score))
new=pd.DataFrame({'标签':i,
'类型':'线性',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##指数
x_cz_2=jj[['自变量']].values.tolist()
y_cz_2=jj[['因变量']].values.tolist()
x_cz_2=sum(x_cz_2,[])
y_cz_2=sum(y_cz_2,[])
L=np.polyfit(x_cz_2, np.log(y_cz_2), 1)
Z=np.polyval(L,x_cz_2)
true=np.exp(Z)
score = r2_score(y_cz_2,true, multioutput='raw_values')
print('指数:'+str(score))
new=pd.DataFrame({'标签':i,
'类型':'指数',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
# ##二次
# x_cz_2=jj[['自变量']].values.tolist()
# y_cz_2=jj[['因变量']].values.tolist()
# x_cz_2=sum(x_cz_2,[])
# y_cz_2=sum(y_cz_2,[])
# L=np.polyfit(x_cz_2, y_cz_2, 2)
# print(L)
# Z=np.polyval(L,x_cz_2,)
# score = r2_score(y_cz_2, Z, multioutput='raw_values')
# print('二次:'+str(score))
# new=pd.DataFrame({'标签':i,
# '类型':'二次',
# 'r2':score,
# '系数':[L]})
# df_d=df_d.append(new,ignore_index=(True))
##幂函数
x_cz_2=jj[['自变量']].values.tolist()
y_cz_2=jj[['因变量']].values.tolist()
x_cz_2=sum(x_cz_2,[])
y_cz_2=sum(y_cz_2,[])
L=np.polyfit(np.log(x_cz_2), np.log(y_cz_2), 1)
Z=np.polyval(L,np.log(x_cz_2))
true=np.exp(Z)
score = r2_score(y_cz_2,true, multioutput='raw_values')
print('幂函数:'+str(score))
new=pd.DataFrame({'标签':i,
'类型':'幂函数',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##对数
x_cz_2=jj[['自变量']].values.tolist()
y_cz_2=jj[['因变量']].values.tolist()
x_cz_2=sum(x_cz_2,[])
y_cz_2=sum(y_cz_2,[])
L=np.polyfit(np.log(x_cz_2), y_cz_2, 1)
Z=np.polyval(L,np.log(x_cz_2))
score = r2_score(y_cz_2,Z, multioutput='raw_values')
print('对数:'+str(score))
new=pd.DataFrame({'标签':i,
'类型':'对数',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##复合函数
x_cz_2=jj[['自变量']].values.tolist()
y_cz_2=jj[['因变量']].values.tolist()
x_cz_2=sum(x_cz_2,[])
y_cz_2=sum(y_cz_2,[])
L=np.polyfit(x_cz_2,np.log(y_cz_2), 1)
Z=np.polyval(L,x_cz_2)
true=np.exp(Z)
score = r2_score(y_cz_2,true, multioutput='raw_values')
print('复合函数:'+str(score))
new=pd.DataFrame({'标签':i,
'类型':'复合函数',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
##生长
x_cz_2=jj[['自变量']].values.tolist()
y_cz_2=jj[['因变量']].values.tolist()
x_cz_2=sum(x_cz_2,[])
y_cz_2=sum(y_cz_2,[])
L=np.polyfit(x_cz_2, np.log(y_cz_2), 1)
Z=np.polyval(L,x_cz_2)
true=np.exp(Z)
score = r2_score(y_cz_2,true, multioutput='raw_values')
print('生长:'+str(score))
new=pd.DataFrame({'标签':i,
'类型':'生长',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
# ##三次
# x_cz_2=jj[['自变量']].values.tolist()
# y_cz_2=jj[['因变量']].values.tolist()
# x_cz_2=sum(x_cz_2,[])
# y_cz_2=sum(y_cz_2,[])
# L=np.polyfit(x_cz_2, y_cz_2, deg=3)
# Z=np.polyval(L,x_cz_2)
# score = r2_score(y_cz_2,Z,multioutput='raw_values')
# print('三次:'+str(score))
# new=pd.DataFrame({'标签':i,
# '类型':'三次',
# 'r2':score,
# '系数':[L]})
# df_d=df_d.append(new,ignore_index=(True))
# ##S函数
# x_cz_2=jj[['自变量']].values.tolist()
# y_cz_2=jj[['因变量']].values.tolist()
# x_cz_2=sum(x_cz_2,[])
# x_cz_3 = [1/x for x in x_cz_2]
# y_cz_2=sum(y_cz_2,[])
# L=np.polyfit(x_cz_3, np.log(y_cz_2), 1)
# Z=np.polyval(L,x_cz_3)
# true=np.exp(Z)
# score = r2_score(y_cz_2,true,multioutput='raw_values')
# print('S函数:'+str(score))
# new=pd.DataFrame({'标签':i,
# '类型':'S函数',
# 'r2':score,
# '系数':[L]})
# df_d=df_d.append(new,ignore_index=(True))
##逆函数
x_cz_2=jj[['自变量']].values.tolist()
y_cz_2=jj[['因变量']].values.tolist()
x_cz_2=sum(x_cz_2,[])
x_cz_3 = [1/x for x in x_cz_2]
y_cz_2=sum(y_cz_2,[])
L=np.polyfit(x_cz_3, y_cz_2, 1)
Z=np.polyval(L,x_cz_3)
score = r2_score(y_cz_2,true,multioutput='raw_values')
print('逆函数:'+str(score))
new=pd.DataFrame({'标签':i,
'类型':'逆函数',
'r2':score,
'系数':[L]})
df_d=df_d.append(new,ignore_index=(True))
df_zh=df_d.sort_values('r2', ascending=False).groupby('标签', as_index=False).first()
ff=df_zh
# second=df_e[(df_e['类型']=='二次')]
j=0
while j < len(a):
gg=ff.iloc[[j]].values.tolist()
gg =sum(gg,[])
if gg[1] == '二次':
x=fw
y_sh=gg[3][0]*x**2+gg[3][1]*x+gg[3][2]
formu_s='y='+str(gg[3][0])+str('x^2+')+str(gg[3][1])+str('x')+str('+(')+str(gg[3][2])+str(')')
elif gg[1] == '线性':
x=fw
y_sh=gg[3][0]*x+gg[3][1]
formu_s='y_zh='+str(gg[3][0])+str('x')+str('+(')+str(gg[3][1])+str(')')
elif gg[1] == '指数':
x=fw
y_sh=np.exp(gg[3][0]*x+gg[3][1])
formu_s='y='+str(np.exp(gg[3][1]))+str('e')+'^'+str(gg[3][0]) +'x'
elif gg[1] == '幂函数':
x=fw
y_sh=np.exp(gg[3][1]+(np.log(x)*gg[3][0]))
formu_s='y='+str(np.exp(gg[3][1]))+str('x')+'^'+str(gg[3][0])
elif gg[1] == '对数':
x=fw
y_sh=gg[3][1]+(np.log(x)*gg[3][0])
formu_s='y='+str(gg[3][1])+'+'+str(gg[3][0])+'In(x)'
elif gg[1] == '生长':
x=fw
y_sh=np.exp(gg[3][0]*x+gg[3][1])
formu_s='y='+'e^('+str(gg[3][0])+str('x')+str('+(')+str(gg[3][1])+str('))')
elif gg[1] == '三次':
x=fw
y_sh=gg[3][0]*x**3+gg[3][1]*x**2+gg[3][2]*x+gg[3][3]
formu_s='y='+str(gg[3][0])+str('x^3+')+str(gg[3][1])+str('x^2+')+str(gg[3][2])+str('x')+str('+(')+str(gg[3][3])+str(')')
elif gg[1] == 'S函数':
x=fw
y_sh=np.exp(gg[3][0]*(x)**(-1)+gg[3][1])
formu_s='y='+'e^('+str(gg[3][0])+str('(1/x)')+str('+(')+str(gg[3][1])+str('))')
elif gg[1] == '逆函数':
x=fw
y_sh=gg[3][0]*(x)**(-1)+gg[3][1]
formu_s='y='+str(gg[3][0])+str('(1/x)')+str('+(')+str(gg[3][1])+str(')')
elif gg[1] == '复合函数':
x=fw
y_sh=np.exp(gg[3][1]+(gg[3][0]*x))
formu_s='y='+str(np.exp(gg[3][1])) +'*'+str(np.exp(gg[3][0])) +'^x'
gg.append(formu_s)
del gg[3]
gg=[gg]
df_a=df_a.append(gg,ignore_index=(True))
# if gg[1] == '二次':
# x=np.arange(0.15,0.4,0.002)
# y_nh=gg[3][0]*x**2+gg[3][1]*x+gg[3][2]-x
# formu_n='y_cz='+str(gg[3][0])+str('x^2+')+str(gg[3][1])+str('x')+str('+(')+str(gg[3][2])+str(')')+'-x'
# elif gg[1] == '线性':
# x=np.arange(0.15,0.4,0.002)
# y_nh=gg[3][0]*x+gg[3][1]-x
# formu_n='y_cz='+str(gg[3][0])+str('x')+str('+(')+str(gg[3][1])+str(')')+'-x'
# elif gg[1] == '指数':
# x=np.arange(0.15,0.4,0.002)
# y_nh=np.exp(gg[3][0]*x+np.log(gg[3][1]))-x
# # formu=str(gg[3][0])+str('x')+str('+(')+str(gg[3][1])+str(')')
# else :
# x=np.arange(0.15,0.4,0.002)
# y_nh=np.exp(gg[3][0]*x+np.log(gg[3][1])) -x
# if gg[5] == '二次':
# x=np.arange(0.15,0.4,0.002)
# y_sh=gg[7][0]*x**2+gg[7][1]*x+gg[7][2] -x
# formu_s='y_zh='+str(gg[7][0])+str('x^2+')+str(gg[7][1])+str('x')+str('+(')+str(gg[7][2])+str(')')+'-x'
# elif gg[5] == '线性':
# x=np.arange(0.15,0.4,0.002)
# y_sh=gg[7][0]*x+gg[7][1] -x
# formu_s='y_zh='+str(gg[7][0])+str('x')+str('+(')+str(gg[7][1])+str(')')+'-x'
# elif gg[5] == '指数':
# x=np.arange(0.15,0.4,0.002)
# y_sh=np.exp(gg[7][0]*x+np.log(gg[7][1])) -x
# else :
# x=np.arange(0.15,0.4,0.002)
# y_sh=np.exp(ff[7][0]*x+np.log(ff[7][1])) -x
# fig11=plt.figure(num=11,figsize=(20,17))
# ax11=fig11.add_subplot(111)
#调整保存图片的大小
plt.figure(figsize=(20, 15))
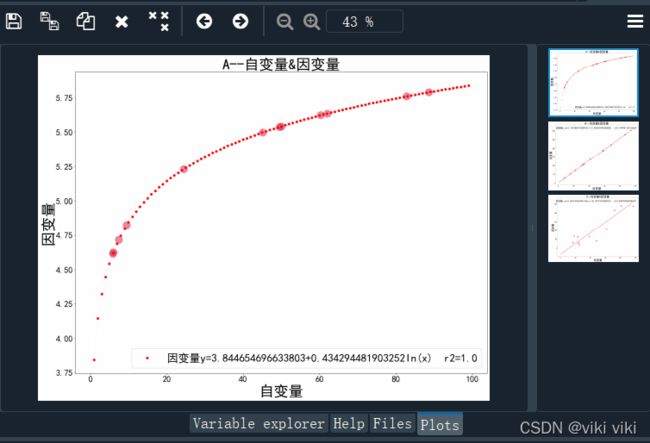
plt.plot(x,y_sh,'r-.o',label=y_因变量+formu_s+' r2='+str(gg[0][2]),linewidth=0.05)
plt.tick_params(labelsize=23)
plt.xlabel(x_自变量,fontsize=40)
plt.ylabel(y_因变量,fontsize=40)
plt.title(str(gg[0][0])+'--'+x_自变量+'&'+y_因变量,fontsize=40) #要用plt调动title
plt.legend(fontsize=30)
x2=data_df[(data_df['标签']==gg[0][0])][['自变量']]
y2=data_df[(data_df['标签']==gg[0][0])][['因变量']]
colors2 = '#DC143C'
area = np.pi * 6**2.7 # 点面积
# 画散点图
plt.scatter(x2, y2, s=area, c=colors2, alpha=0.5)
plt.savefig('')
plt.savefig(io_1+'/%s.jpg'%(gg[0][0]), bbox_inches='tight')
plt.show()
# plt.close()
j=j+1
if j > len(a)-1:
break
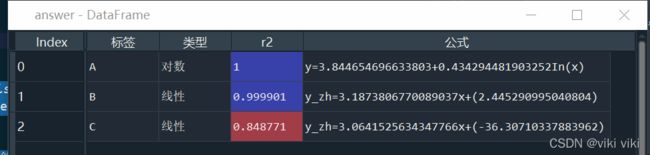
df_a.columns= ['标签','类型', 'r2','公式']
return df_a三、开始调用代码,验证成果
import pandas as pd
import numpy as np
#需要加载的数据集
io=r'C:\Users\**\Desktop\测试集.xlsx'
data_df=pd.read_excel(io,sheet_name='测试数据集')
x_自变量='自变量'
y_因变量='因变量'
io_1=r'C:\Users\**\Desktop\临时文件'
fw=np.arange(1,100,1)
answer=analysis_of_regression(data_df,x_自变量,y_因变量,fw,io_1)撒花,完美调用~。本篇都是原创的代码,如果代码好用请点赞!