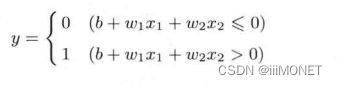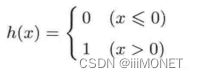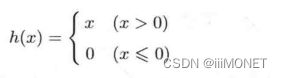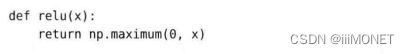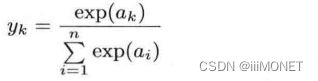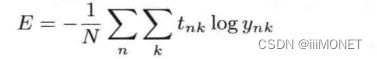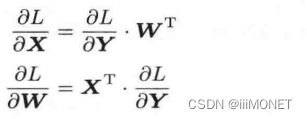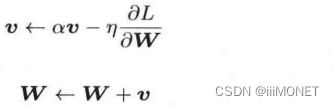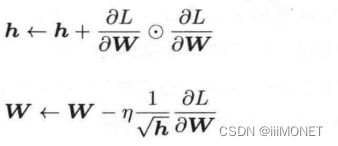笔记《深度学习入门：基于Python的理论与实现》

第一章 Python入门

1、使用的外部库

2、python基础

第二章 感知机

感知机作为神经网络的起源算法，学习感知机构造

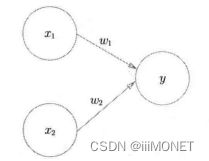
1、感知机运行原理

 权重、阈值

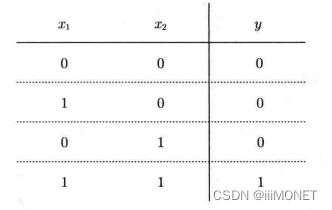
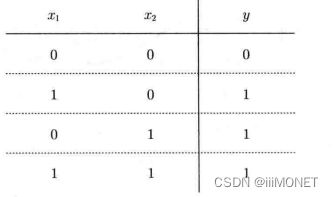
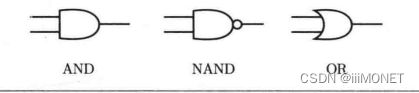
2、与门、与非门、或门

 3、感知机实现：引入权重和偏置

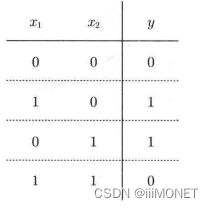
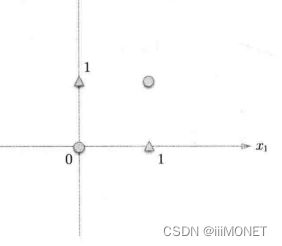
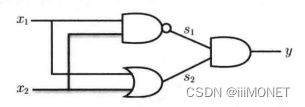
4、异或门

 

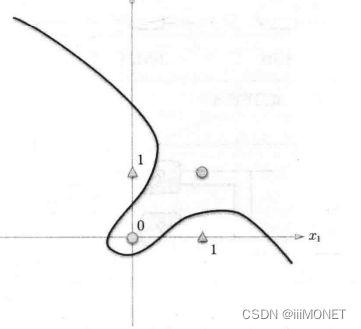
无法使用单层实现，线性——>非线性，使用多层感知机。

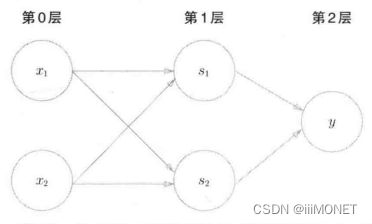
5、多层感知机

通过叠加层，感知机能进行更灵活的表示

单层感知机只能表示线性空间，多层感知机能表示非线性空间

 

多层感知机在理论上可以表示计算机

第三章 神经网络

设定权重，人工——>自动从数据中学习到合适的权重参数

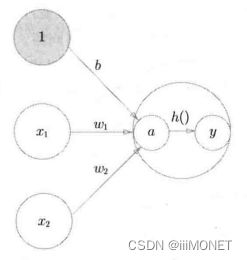
1、感知机——>神经网络

将感知机用另一种函数表现，h(x)为激活函数，作用在于决定如何激活输入信号的总和

感知机和神经网络的主要区别在于激活函数

 

 

2、激活函数 

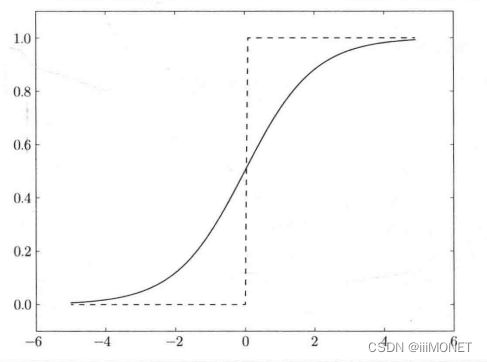
 （1）sigmoid函数

 

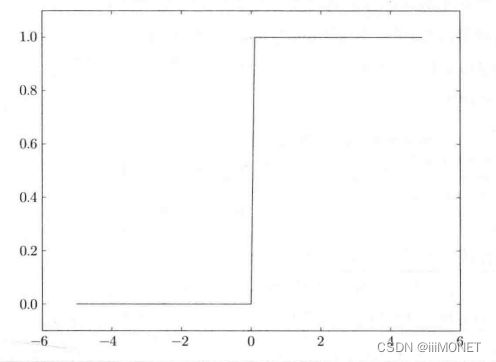
 （2）阶跃函数

y.astype(np.int)

 

 比较Sigmoid和阶跃函数

感知机中神经元之间流动的是0或1的二元信号，神经网络中流动的是连续的实数值信号；

输入小时，输出接近0；输入大时，输出接近1，输入信号为重要信息时，上述激活函数会输出较大的值，都是非线性函数——激活函数不能使用线性函数，否则各层叠加之后可用单层代替

（3）ReLU函数

 

 np.maximum(0,x)

 3、3层神经网络的实现

多维数组运算：A= np.array([1,2,3]) , A.shape , np.ndim(A) , np.dot(A,B)点乘

前向神经网络：输入——>输出

神经网络的运算可以作为矩阵乘法运算打包进行

分类问题、回归问题

 

输出层的激活函数，回归问题中一般用恒等函数，分类问题中一般用softmax函数

4、输出层的设计

输出函数：

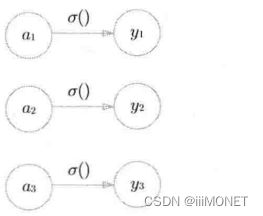
（1）恒等函数

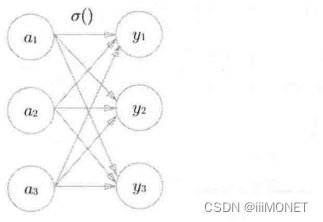
（2）softmax函数

a-np.max(a)，y不变，防止溢出 

softmax函数输出在0到1之间，函数输出值的总和时1，可以把softmax函数输出解释为概率，用 softmax表示分类概率大小顺序和输出值大小顺序相同，可在推理阶段省略softmax()函数

输出神经元的数量一般设定为类别数量

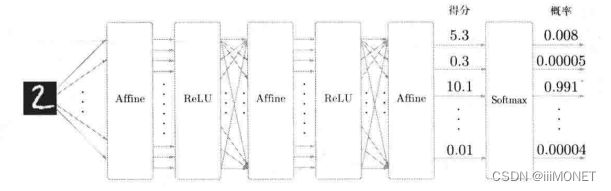
5、手写数字识别

推理处理/前向传播

MNIST数据集，28px×28px，0~255，0~9共10类

读入MNIST数据；读入权重参数；进行推理；评价识别精度

批处理（批，batch）：打包式输入，减轻数据总线的负荷，批处理一次性计算大型数组要比分开逐步计算各个小型数组速度更快

np.argmax()：获取最大元素的索引——predict对应的最大的数（0~9）

第四章 神经网络的学习

学习：从训练数据中自动获取最优参数的过程——以损失函数为基准，找出能使它的值达到最小的权重参数

1、从数据中学习

数据驱动，数据——模式

机器学习与深度学习： 深度学习/端到端机器学习（end_to_end machine learning）

测试数据、训练数据/监督数据——>测试泛化能力

过拟合（over fitting）：只对某个数据集过度拟合的状态

2、损失函数

损失函数（loss function）：神经网络以某个指标为线索寻找最优权重参数，所用指标为损失函数，可以使用均方误差、交叉熵误差等

（1）均方根误差

one-hot表示：正确解标签表示为1，其他标签表示为0

（2）交叉熵误差

 交叉熵误差的值由正确解标签对应的输出结果决定，正确解标签对应的输出越大，E的值越接近0

delta：保护性对策 

（3）mini-batch学习

机器学习使用训练数据进行学习，就是针对训练数据计算损失函数的值，如果要求所有训练数据的损失函数的总和，则：

np.random.choice()——>索引——>对应mini-batch——>计算损失函数

如果是标签形式的y：-np.sum(np.log(y[np.arange(batch_size),t]+1e-7))/batch_size

寻找最优参数（权重、偏置）时，要寻找使损失函数的值尽可能小的参数，在进行神经网络学习时，不能将识别精度作为指标，如果以识别精度为指标，参数的倒数在绝大多是地方会变成0，导致参数无法更新

阶跃函数导致损失函数的值不会发生变化，sigmoid函数的导数在任何地方都不为0

3、数值微分

 中心差分

h过小：会出现舍入误差 ；差分：不能完全替代导数（解析性导数）

偏导数：将多个变量中的某一个变量定为目标变量

4、梯度

梯度（gradient）：由全部变量的偏导数汇总而成的向量

 梯度指向各点处的函数值降低的方向，即函数值减小最多的方向

（1）梯度法

学习时寻找最优参数——损失函数取最小值时的参数（使用梯度寻找，减小值最多≠指向最小值）

鞍点（saddle point）：函数极小值、最小值，梯度为0

寻找最小值：梯度下降法；寻找最大值：梯度上升法

学习率需要事先确定，影响最终结果，神经网络学习中一般会一边改变学习率一边确定学习是否正确进行，学习率过大——发散成一个很大的数，学习率过小——基本不更新；学习率，超参数，尝试多个值以便找到一种可以使学习顺利进行的设定

（2）神经网络的梯度 

损失函数关于权重参数的梯度

simpleNet类：predict，loss（predict、softmax输出函数、cross_entropy_error交叉熵误差计算损失函数）

 

5、学习算法的实现

神经网络学习步骤：数据选择——>计算梯度——>更新权重——>……（随机梯度下降法）

 

（1）两层神经网络的类

 （784，100，10）

如何设置权重参数的初始值时关系到神经网络能否学习成功的重要问题，np.random.randn()使用符合高斯分布的随机数进行初始化

 

 （2）mini-batch实现

 通过反复学习可以使损失函数的值逐渐减小

（3）基于测试数据的评价

确认是否能正确识别训练数据以外的其他数据，确认是否会发生过拟合（泛化能力）

 

 训练精度和测试精度基本没有差异，没有过拟合现象

第五章 误差反向传播算法

误差反向传播算法能高效计算权重参数的梯度，基于数学式和计算图进行理解

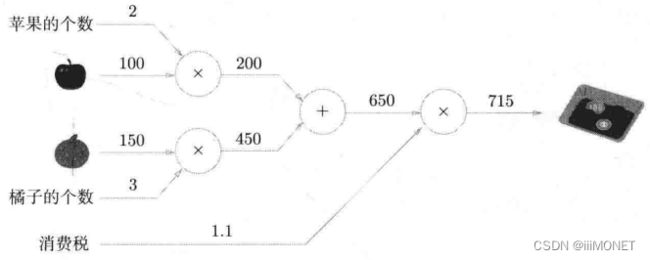
1、计算图

从左到右计算：正向传播——从右到左反向传播 

计算图可以集中精力于局部计算，通过局部计算使各节点致力于简单计算，简化问题

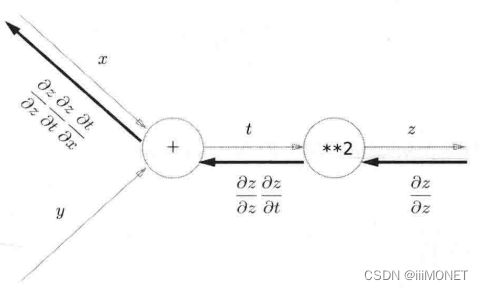
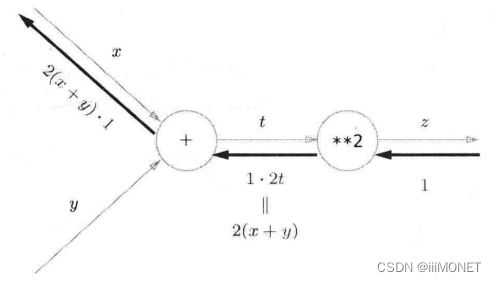
2、链式法则

计算图的反向传播：

链式法则：

 基于链式法则

 带入例子中的函数

3、反向传播

下游<——上游

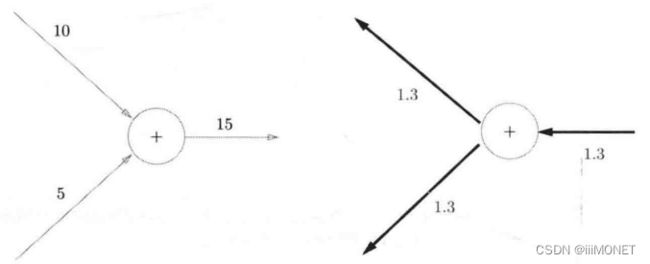
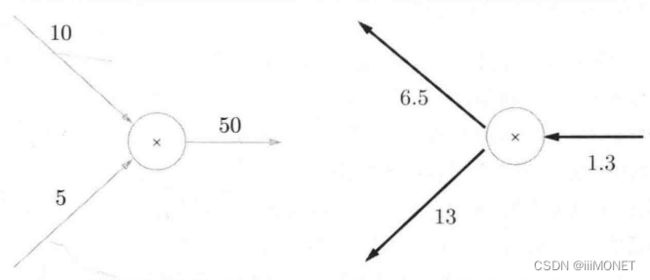
加法：将上游值原封不动输出到下游

乘法：反向传播会乘以输入信号的翻转值

（z=xy）

 

4、简单层的实现

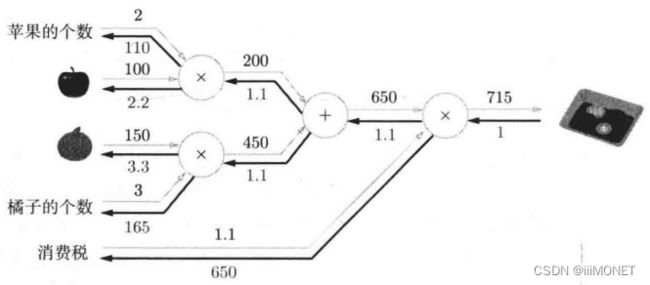
（1）乘法层

（2）加法层

   add_apple_orange_layer = AddLayer()

5、激活函数的实现

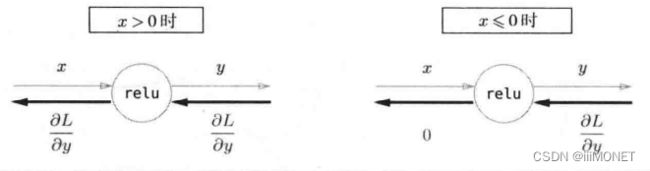
（1）ReLU层

 class ReLu：

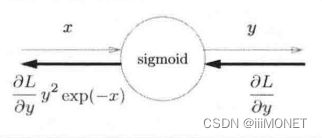
（2）Sigmoid层

  class Sigmod：

6、Affine/Softmax层的实现

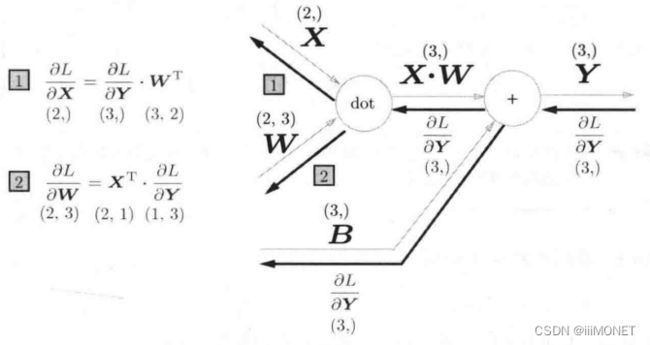
（1）Affine层

X和∂L/∂X形状相同，Y和∂L/∂Y形状相同 

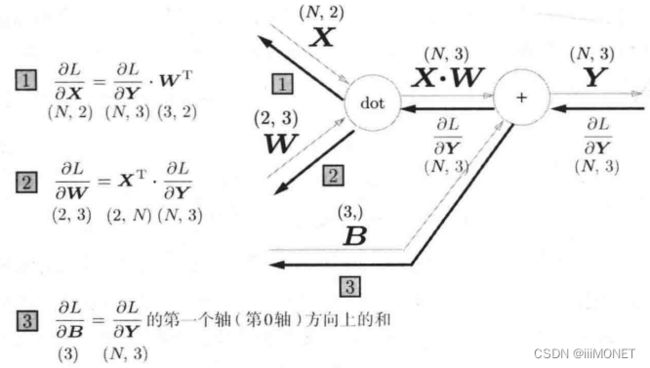
（2）批版本的Affine层

N个数据进行正向传播，X形状（N，2）

np.sum(dY,axis=0)                         class Affine：

（3）Softmax-with-Loss层

推理阶段不用Softmax，学习阶段用Softmax

交叉熵误差设计

神经网络的反向传播会把差分表示的误差传递给前面的层，需要把神经网络的输出和标签的误差高效传递给前面的层

7、误差反向传播法的实现

组装已实现的层构建神经网络

mini-batch——>计算梯度——>更新参数——>重复

数值微分被误差反向传播方法取代，数值微分被用来确认反向传播法的实现是否正确，即梯度确认（gradient check）

 

 表明反向误差传播求梯度正确

使用误差反向传播法的学习：

  

第六章 与学习线相关的技巧

1、参数更新

（1）随机梯度下降法SGD

 

SGD在某些情况效率低，根本原因是梯度方向没有指向最小值的方向

（2）Momentum

 

 （3）AdaGrad

学习率衰减：对着学习的及逆行，使学习率逐渐减小

 （4）Adam

Momentum+AdaGrad，进行超参数的偏差校正

超参数：学习率、一次momentum系数、二次momentum系数

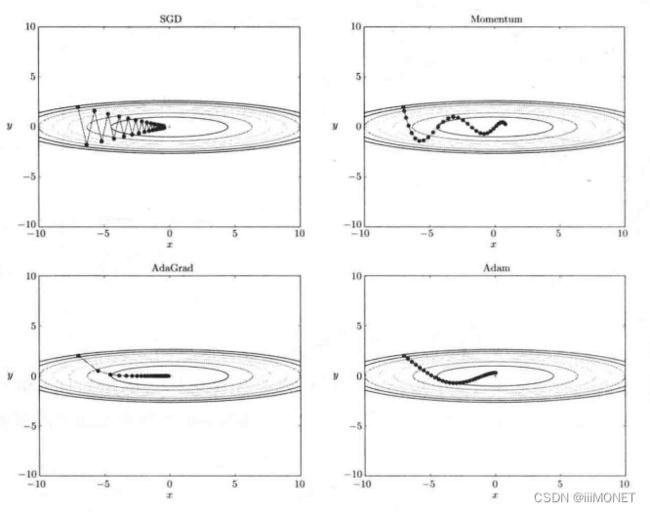
实验结果会随学习率等超参数、神经网络的结构的不同发生变化，一般与SGD相比，Momentum、Adam、AdaGrad可以学习得更快，有时最终识别精度也更高

2、权重初始值

防止权重均一化，必须随机生成初始值

权值衰减：以减小权重参数的值为目的进行学习，通过减小权重参数的值抑制过拟合的发生

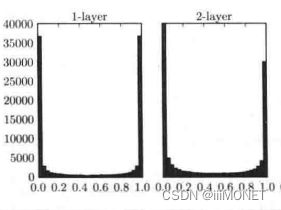
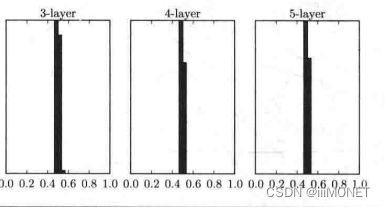
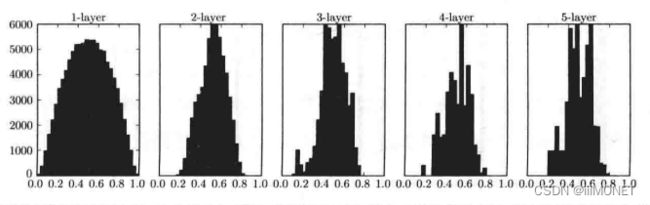
（1）隐藏层的激活值分布

梯度消失：偏向0和1的数据分布会造成反向传播中梯度值不断变小，最后消失

标准差为1的高斯分布、标准差0.01的高斯分布、Xavier初始值：

 

（2）权重初始值

ReLU激活函数  He初始值：np.sqrt(2/n)

sigmoid、tanh等S型曲线函数  Xavier初始值：np.sqrt(1/n)

3、batch normalization

4、正则化

5、超参数的验证

第七章 卷积神经网络

1、整体结构

2、卷积层

3、池化层

4、卷积层和池化层的实现

5、CNN的实现

6、CNN的可视化

7、具有代表性的CNN

（1）LeNet

（2）AlexNet

第八章 深度学习

1、加深网络

2、深度学习进展

3、深度学习的高速化

4、深度学习应用案例

5、深度学习前景