图论最短路径专题(力扣743、5888)
第八十五天 --- 图论最短路径专题(力扣743、5888)
- 题目一
-
- 朴素Dijkstra解决无负权边的单源最短路径问题
-
- 思路
- 代码
-
- 邻接矩阵
- 邻接表
- 复杂度
- Floyd解决多源点最短路径问题
-
- 思路
- 代码
- Bellman Ford算法解决带有负权边或者有限制的最短路径问题
-
- 思路
-
- 带有额外限制:尤其是对路径经过的边数(或点数)限制
- 无限制图(当有负权边只能用这个算法或者SPFA)
-
- 状态
- 初始值
- 转移
- 找答案
- 优化
- 代码
- 题目二
-
- 堆优化Dijkstra解决无负权边的单源最短路径问题
-
- 思路:自己封装堆(小根堆为例)
- 代码
- SPFA:Bellman Ford算法的优化
-
- 思路:动态逼近法
- 代码
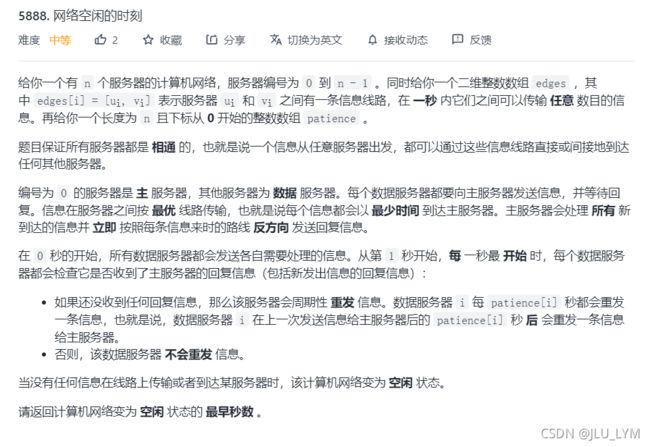
题目一
力扣:743. 网络延迟时间
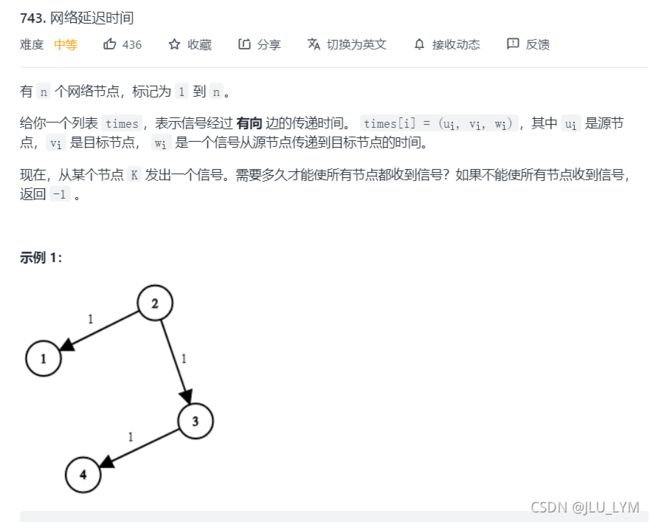

本题其实就是让求各个点到源点最短路,且最短路中要找到最大者。
朴素Dijkstra解决无负权边的单源最短路径问题
思路
1、要求的是,图中各个点到源点的最短距离,所以维护一个dis数组,来记录最短距离。
2、还要维护两个集合,一个是未走过的点,一个是已经走过的点(即已经找到最短距离的点),所以有一个bool类型的visit来维护这两个集合。
3、dis数组因为是求最短路径,所以初始值为无穷大(可以根据题意算,也可以取INT_MAX/2,但不要太接近INT_MAX,防止溢出),但是源点到源点距离是0,所以得改一下,这样也保证了从源点开始。
4、每一次我要扩充我已经到过的集合,直到找到所有点为止。
5、因为需要最短距离,故在没走过的点中,挑选dis值最小的,也就是离源点最近的点,作为目标扩充进已经走过的点中即可。
6、那么因为这个点被选中,源点到他的最短距离已经有了,那么可不可能,找到从这个新的点出发的所有路径,路径终点中没走过的点到源点的距离更小了呢,因为dis是动态维护的,说大白话就是每次有值在变动咱们都要去看一下,最小值能否更新,所以用之前说的方法求一下新的距离,去dis更新一下最小值即可。
7、如果上述过程看的迷糊,我推荐大家根据这篇博客:图解Dijkstra,边按照上述的过程看,边对应着真实的图看,这样效果更好。
代码
!!!!!!!!!!!注意!!!!!!!!!!!!!
一定要看好是无向图还是有向图,前者一条边得正反存储两次,后者只要存一次就行
邻接矩阵
注意:如果图特别稠密,推荐用这个方法存储图;如果图上权值都不一致,推荐这个方法存储图。
class Solution {
public:
const int MAX = INT_MAX / 2;//预设极大值,不要太大,容易溢出
bool visit[150];//需要标志出已经判断完最短路径的点
int dis[150];//到每个点的最短距离
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
int times_size = times.size();
vector<vector<int>> edge(n + 1, vector<int>(n + 1, MAX));//邻接矩阵存储,用于稠密的图,便于存储权值,有权值推荐这样或者用类存储,初始值要设成这个
//初始值要设置成MAX,因为有的边不存在,但是为了配合求最小值,也要设置成无穷大
for (int i = 0; i < times_size; i++) {//建图
int u = times[i][0];
int v = times[i][1];
int w = times[i][2];
edge[u][v] = w;
}
for (int i = 1; i <= n; i++) {//初始化
visit[i] = false;
dis[i] = MAX;
}
//Dijkstra
dis[k] = 0;//保证程序从初始点运行,且这样符合题意
while (true) {
int x = -1;
for (int i = 1; i <= n; i++) {
if (!visit[i] && (x == -1 || dis[i] < dis[x])) {
x = i;//寻找离源点最近的点
}
}
if (x == -1) {//所有点找到后结束
break;
}
visit[x] = true;//走到了
for (int i = 1; i <= n; i++) {
if (visit[i]) {//已经走过的点不访问
continue;
}
dis[i] = min(dis[i], dis[x] + edge[x][i]);//用这个点更新其他没走过的点
}
}
//找答案
int ans = 0;
for (int i = 1; i <= n; i++) {
ans = max(ans, dis[i]);
}
return ans == MAX ? -1 : ans;
}
};
邻接表
注意:稀疏图建议用这个;边的权值都一致建议用此方法,权值不一致得但用map(这里注意一下不是unordered_map,因为pair只能排序,不能求哈希值)单独存储,时间复杂度大;如果点太多也得用此方法。
class Solution {
public:
const int MAX = INT_MAX / 2;//预设极大值,不要太大,容易溢出
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
int times_size = times.size();
vector<vector<int>> edge(n);//邻接表
map<pair<int, int>, int> edge_value;//存储权值,每次取用时间复杂度在O(lgN)
vector<bool> visit(n, false);//含义同上
vector<int> dis(n, MAX);
for (int i = 0; i < times_size; i++) {//建图
int u = times[i][0];
int v = times[i][1];
int w = times[i][2];
edge[u - 1].push_back(v - 1);//为了存储方便,这里改为编号从0开始
edge_value.insert(pair<pair<int, int>, int>(make_pair(u - 1, v - 1), w));
}
//Dijkstra
dis[k - 1] = 0;
while (true) {
int x = -1;
for (int i = 0; i < n; i++) {
if (!visit[i] && (x == -1 || dis[i] < dis[x])) {
x = i;
}
}
if (x == -1) {
break;
}
visit[x] = true;
for (int i : edge[x]) {//不用访问所有的点,只要访问和他连接的点就行了
if (!visit[i]) {
int values = edge_value.at(make_pair(x, i));
dis[i] = min(dis[i], dis[x] + values);
}
}
}
int ans = 0;
for (int i = 0; i < n; i++) {
ans = max(ans, dis[i]);
}
return ans == MAX ? -1 : ans;
}
};
复杂度

值得注意的是:
1、其实绝大多数求解最短路的题目,我们会这个方法就足够了,但是一旦遇到极大的数据量,比如十万条数据冲击下,这个算法时间复杂度就太高了,所以采用堆优化它。
2、我们可以通过在得到目标处最短路径之后,用DFS逆推回到源点,来找到所有符合要求的路径;或者通过记录前缀点来找到某一条符合要求的路径。
Floyd解决多源点最短路径问题
Floyd是非常经典的求多源点最短路径问题,他的优点就在于代码极为简单,好理解,但是缺点也极为明显,时间复杂度到达了惊人的O(N^3)。
思路
1、Floyd算法要用邻接矩阵存储。
2、Floyd是经典的由DP定义出来的算法,dp[i][j]表示从i到j的最短路径,初始化时,只有自己到自己是0,别的为了求最小值,都赋值无穷大。转移的时候,从i走到j,要去枚举所有的中间节点,他可能是枚举所有可能的中转站,在所有中转站中转的结果中找到最小,作为这个状态的结果。
3、找答案时候,只需要知道源点i汇点j,则edge[i][j]即为答案。
4、综上:枚举的时候 中转站-源点-汇点;从i到j,枚举全部中转站p,看各个i到p距离+p到j距离,找到最小即可。
代码
class Solution {
public:
const int inf = INT_MAX / 2;
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
int times_size = times.size();
vector<vector<int>> edge(n + 1, vector<int>(n + 1));
for (int i = 1; i <= n; i++) {//初始化
for (int j = 1; j <= n; j++) {
edge[i][j] = i == j ? 0 : inf;
}
}
for (int i = 0; i < times_size; i++) {//建图
int u = times[i][0];
int v = times[i][1];
int w = times[i][2];
edge[u][v] = w;
}
//Floyd:中转站-源点-汇点
for (int p = 1; p <= n; p++) {//枚举所有中转站
for (int i = 1; i <= n; i++) {//枚举所有源点
for (int j = 1; j <= n; j++) {//枚举所有汇点
edge[i][j] = min(edge[i][j], edge[i][p] + edge[p][j]);//转移方程式
}
}
}
int ans = 0;//找答案
for (int i = 1; i <= n; i++) {
ans = max(ans, edge[k][i]);//源点是k
}
return ans == inf ? -1 : ans;
}
};
值得注意的是:如果只追求代码好写,并且题目本身数据并不是很特别、量不大,那么用Floyd就行,但是最好用改良版Dijkstra循环n次枚举所有源点来替代Floyd,这样效果更好。
Bellman Ford算法解决带有负权边或者有限制的最短路径问题
思路
带有额外限制:尤其是对路径经过的边数(或点数)限制
一旦最短路径求解的时候,被附加上了额外的限制,这时候就要想起由DP定义的算法了,将限制作为状态加进去,进行DP即可(如果对路径经过的边数(或点数)限制,只需要用原始定义就行),例子:力扣787。
无限制图(当有负权边只能用这个算法或者SPFA)
首先要明白,bellman ford用DP定义
状态
1、k表示:当前枚举的路径里面有最多k条边(说句人话,就是我当前枚举从源点到各个点i,路径上经过的边数=k,求出满足这个条件的路径长度存储起来,如果不满足也不要紧,会进入无意义点,我们再对无意义点初始值设置成无穷大就不会影响)
2、i表示:从源点到 i
初始值
只有dp[0][k]=0 k代表源点,只有从源点到源点,并且走过的路径长度是0时候,花费是0,别的点为了配合求最小值都是正无穷。
转移
1、外层枚举k,表示现在找的路径是距离源点k的,他是要从上一次即k-1来
2、内层按理说应该建一张图,然后找到所有指向i的边,找到边的源头,最后枚举所有i即可。但是这不就是找到所有的边吗,所以直接枚举边就行,此算法关注点就在于对边的枚举。
3、综上,转移方程是
dp[k][i] = min(dp[k][i], dp[k - 1][j] + price);
//边j->i,price指的是权值
找答案
最后,对于每个点,他到源点的路径,用路径上的边数,从小到大的给枚举出来(利用k),不同边数对应的距离存储在不同的k值,相同的i值,的地方。即枚举k保持i不动,最后找到最终的最小值。
优化
1、因为每一次都是从k-1转移到k,所以第一个维度没啥用,省略掉,只需要每次拷贝一下上次的状态(也就是边数k-1)就行。
2、关键的来了,能否理解,豁然开朗就看这几句话了:
<1> 两个状态,必须两个循环,外层循环就相当于规定了这一轮我们找谁,我们找到源点的路径长度为k的(没有这种路径没关系,会冲入没走过状态,在初始化的时候留了后手,值为无穷大,所以没影响.),这次的值,由上一个状态过来即(边数k-1,到j)+(j->i的花费)这其实也是内部循环直接每次枚举所有边就行了的原因。
<2>内部就是循环找边,原因上面分析过了
<3>上面说的是每一步,我们抽出来一个点i(非源点),就是按照k从1到n枚举出来所有长度的路径(路径不存在不要紧,就是无穷大,因为初始值的缘故),通过每次取最小值,将新来的路径长度,和原来的最小值二者取最小,这样动态维护下去,出现一个合法路径,就比较一次,最后得到的就是一条最短路径。
代码
注意:此算法其实最关注的是对边的枚举,所以没必要存储图,直接在内层枚举所有边就行。
class Solution {
public:
const int inf = INT_MAX / 2;
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
vector<int> dis(n + 1, inf);//dp转移用的数组
dis[k] = 0;//初始化
/*Bellman Ford算法开始*/
for (int p = 1; p < n; p++) {//枚举经历的边数,n个点最多n-1条边
vector<int> tmp(dis);//拷贝上一次状态
for (vector<int>edge : times) {//枚举所有的边,因为本算法注重对边的枚举
dis[edge[1]] = min(dis[edge[1]], tmp[edge[0]] + edge[2]);//本次转移
}
}
int ans = 0;
for (int i = 1; i <= n; i++) {
ans = max(ans, dis[i]);
}
return ans == inf ? -1 : ans;
}
};
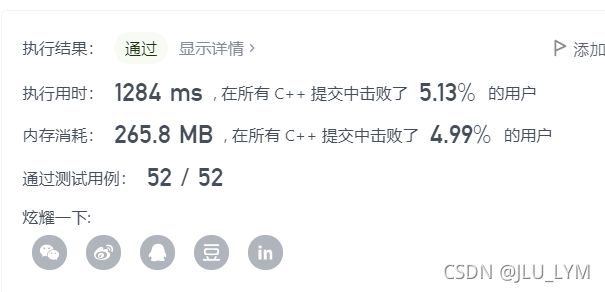

值得注意的是:正常一旦遇到负权边了,首选这个算法;一旦遇到带有限制的最短路问题,在原本DP基础上,再加相应的状态,找转移就行了(特别的一旦限制了最短路径中间节点个数或者边数,首选此算法,因为他朴素的定义恰好合适);但是本算法时间复杂度较高,要么优化(spfa),要么在不遇到Dijkstra解决不了的时候(有负权边,最短路有限制),使用本算法,剩下时候少用这个算法。以Dijkstra改进算法为主。
题目二
堆优化Dijkstra解决无负权边的单源最短路径问题
(因为这道题边权都一致,所以并未使用邻接矩阵,而是用了邻接表)
1、我们回顾一下朴素Dijkstra算法,每次都要挑选一个dis中最小的点,来加到已走过的集合中,每一次都要遍历所有的点,一旦点数很大很大,接近O(N^2)的时间复杂度,就一定会超时。
2、所以有没有一种结构,能够在不断的增加点和拿取点这个动态过程中,一直为我们维护一个最大值或者最小值,让我们在O(1)内取用,这样上述问题就解决了。
3、所以我们选择了堆结构,这种结构完美适应了上述条件,这样在每次选择最大值或者最小值的时候,我们在O(1)内即可完成。
思路:自己封装堆(小根堆为例)
1、维护一个堆,可以让我们在O(1)内得到一个最大或者最小值,并且不论我们是增加还是删除节点,堆内部都会自动维护一个堆顶,最大或最小。本题求最短路径,所以维护一个小根堆。堆的封装教学见堆排序原理及实现。
2、堆的最重要的两个操作就是,上浮&下沉。
上浮:顾名思义,就是把目标节点尽可能地向上挪,因为是完全二叉树(从1开始存储),所以int father = k>>1;每次除二找父节点,第一要注意别越界,第二要注意当父节点小于本节点之后,就停止,否则交换,继续循环。
下沉:顾名思义,就是把目标节点尽可能地向下挪,计算儿子节点(内部从1开始存储,所以*2为左二子,*2+1为右儿子),注意两个事,第一两个儿子节点不可以越界,第二交换上去的儿子节点必须是两个中最小的。
3、当进入新的节点,放到最后,上浮到合适位置就行;当弹出堆顶,用最后一个元素放在堆顶,下沉一次就可以重新整理一下堆结构,维护一个全新的堆顶;peak()操作就是取堆顶,获得最大或者最小值。
4、因为这个是单源最短路径,所以起点固定,每次都是固定起点到各个终点最短路径,所以在堆中只要维护一个Node类型数组就行,Node内部就是到哪个目标点,以及相应的最短距离。
代码
1、这样用堆操作简化了获得最小值操作,别的部分就不必简化了。
2、在最短路径都有了之后,就按照数学公式来计算就行:
dis[i]*2表示第一个信息走了多久
n1表示总共多少个信息,用(dis[i] * 2) / patience[i];即可算出,但要注意一旦不整除,就得++(通过不断失误才推知)
最后n1-1代表多余的数据, (n1 - 1)*patience[i];表示总共的延时。
3、计算出每个点的时间,答案是最大的时间+1.
4、一旦出错了,调试的时候有技巧,先一点点打断点找是哪块用错了,在逐渐进入各个小函数里面找,直到定位到错误为止。
5、堆中维护一个size ,这个玩意是堆大小,外人绝对不能改,这个是堆内部自己动态维护的。
class Node {
public:
int vertex;//想要到达的点
int dis;//距离
bool operator < (const Node& node) {//定义比较方法
return dis < node.dis;
}
};
class pile {//堆的封装
private:
Node heap[100001];//开足够大(看题目约定),内部从1开始存储,本身是完全二叉树,用数组存储。
int size = 0;//这个是堆内部核心属性,不可以被外人动
public:
void up(int k) {
int fa = k >> 1;
while (fa >= 1) {//防止越界
if (heap[fa] < heap[k]) {//停止条件
break;
}
swap(heap[k], heap[fa]);
k = fa;
fa >>= 1;
}
}
void down(int k) {
int son = k << 1;
while (son <= size) {//两个儿子都要防止越界
if (son + 1 <= size && heap[son + 1] < heap[son]) {//有两个儿子,让最小的上去
son++;
}
if (heap[k] < heap[son]) {
break;
}
swap(heap[k], heap[son]);
k = son;
son <<= 1;
}
}
Node peak() {
return heap[1];
}
void pop() {
heap[1] = heap[size--];
down(1);
return;
}
void add(Node k) {
heap[++size] = k;
up(size);
}
int get_size() {
return size;
}
};
class Dijkstra {
public:
vector<int> dijkstra(vector<vector<int>>& edges, int n, int k) {//点数从1开始
const int inf = INT_MAX / 2;
int edges_size = edges.size();
pile p;
vector<vector<int>> edge(n);//邻接表
vector<bool> visit(n, false);//含义同上
vector<int> dis(n, inf);
for (int i = 0; i < edges_size; i++) {//建图
int u = edges[i][0];
int v = edges[i][1];
int w = 1;
edge[u].push_back(v);//无向图一条边存两次
edge[v].push_back(u);
}
p.add({ k,0 });//把初始节点放进去
while (p.get_size()) {
Node x = p.peak();//获取最小
p.pop();
if (visit[x.vertex]) {
continue;//这里设计很巧,只要这个点走过就continue,所以各个点只要有一个新的状态就加入堆,各个点总有一个最小值,最小值肯定最先出来,后面的距离
//后出但是该点已经走过了,就没有影响
}
visit[x.vertex] = true;
for (int i : edge[x.vertex]) {//更新距离
if (visit[i]) {//走过的点不更新
continue;
}
if (x.dis + 1 < dis[i]) {
dis[i] = x.dis + 1;
p.add({ i,dis[i] });//更新后加入堆
}
}
}
return dis;
}
};
class Solution {
public:
int networkBecomesIdle(vector<vector<int>>& edges, vector<int>& patience) {
Dijkstra dijkstras;
int n = patience.size();
vector<int> dis = dijkstras.dijkstra(edges, n, 0);
vector<int> times(n, 0);
for (int i = 1; i < n; i++) {//这里计算延迟没问题
int n1 = (dis[i] * 2) / patience[i];
if ((dis[i] * 2) % patience[i] != 0) {
n1++;
}
if (n1 >= 1) {
times[i] = dis[i] * 2 + (n1 - 1)*patience[i];
}
else {
times[i] = dis[i] * 2;
}
}
int maxs = 0;
for (int i = 0; i < n; i++) {
maxs = max(maxs, times[i] + 1);
}
return maxs;
}
};

值得注意的是:
1、当边数远大于点数的时候(稠密图),堆优化效果也不是很好
2、我们可以通过在得到目标处最短路径之后,用DFS逆推回到源点,来找到所有符合要求的路径;或者通过记录前缀点来找到某一条符合要求的路径。
SPFA:Bellman Ford算法的优化
(用邻接表存储)
思路:动态逼近法
1、其实说是Bellman Ford的优化,但是我实际写起来她的感觉更类似于Dijkstra。
2、说起来很简单,就是一个用队列维护的BFS思路。
3、我们回想一下Dijkstra,他每一次都是在dis找到一个距离源点最近的点,用它再更新别的为访问过的点,循环n-1次就可以全部找到。
4、我们这个算法不这样,在某一次i点的最短距离被更新了,那么是不是存在可能通过i点把别的点的最短距离也给更新了呢?完全可能,所以,我们要把这样的点(即存在活力的点)加入队列,等到他弹出来后,用它去更新别的点。
5、综上:每次从队列头拿一个点,用他们去更新别的点,一旦某个点被更新了说明,那个点是有潜力的点,可能通过这个点让更多的点找到他们自己的最短路径,故入队,直到队列空了为止,那么说明源点到各个点的路径都最短了,无法继续更新了,就是答案。
6、特别的,如果某个点不可及,那么最后他的值将是初始值,无穷大。
7、这种算法适用于任何正数权值,也可以解决含有负权的图
代码
1、先用SPFA求解最短路,一定要注意无向图再存的时候一定正反存两次!!
2、在最短路径都有了之后,就按照数学公式来计算就行:
dis[i]*2表示第一个信息走了多久
n1表示总共多少个信息,用(dis[i] * 2) / patience[i];即可算出,但要注意一旦不整除,就得++(通过不断失误才推知)
最后n1-1代表多余的数据, (n1 - 1)*patience[i];表示总共的延时。
3、计算出每个点的时间,答案是最大的时间+1.
class SPFA {
public:
vector<int> spfa(vector<vector<int>>& edges, int n, int k) {//点数从1开始
const int inf = INT_MAX / 2;
int edges_size = edges.size();
vector<vector<int>> edge(n);//邻接表
vector<int> dis(n, inf);//距离,初始值无穷大
for (int i = 0; i < edges_size; i++) {//建图
int u = edges[i][0];
int v = edges[i][1];
int w = 1;
edge[u].push_back(v);//无向图
edge[v].push_back(u);
}
/*SPFA算法开始*/
queue<int> q;//队列存储的是可能产生新的变化的点,如果没变化了,说明是答案,队列也就空了
dis[k] = 0;//初始点
q.push(k);//初始化,压入源点
while (!q.empty()) {
int x = q.front();//取一个点
q.pop();
for (int i : edge[x]) {//遍历以这个点为开头的所有边
if (dis[x] + 1 < dis[i]) {//看是否产生更新,1是权值
dis[i] = dis[x] + 1;
q.push(i);//压入i
}
}
}
return dis;
}
};
class Solution {
public:
int networkBecomesIdle(vector<vector<int>>& edges, vector<int>& patience) {
SPFA spfas;
int n = patience.size();
vector<int> dis = spfas.spfa(edges, n, 0);
vector<int> times(n, 0);
for (int i = 1; i < n; i++) {//这里求延迟没问题
int n1 = (dis[i] * 2) / patience[i];//求一共出来了多少信息
if ((dis[i] * 2) % patience[i] != 0) {//经验证发现,如果不整除,会少一条信息
n1++;
}
if (n1 >= 1) {//这里防止0 - 1出负数
times[i] = dis[i] * 2 + (n1 - 1)*patience[i];//第一个信息时间+后续延迟
}
else {
times[i] = dis[i] * 2;
}
}
int maxs = 0;
for (int i = 0; i < n; i++) {
maxs = max(maxs, times[i] + 1);
}
return maxs;
}
};
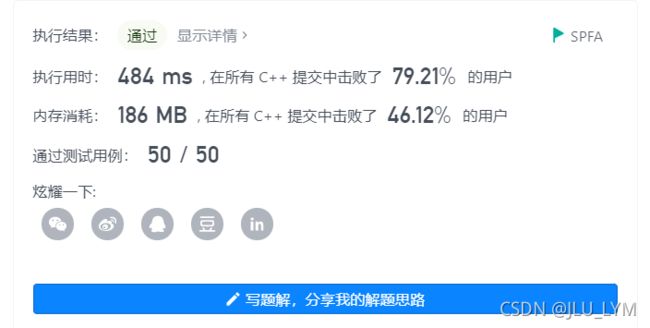

值得注意的是:
在求解有限制的最短路问题时候,尤其是限制中间节点个数时候,spfa就不可以了,并不适用,应该选用bellman Ford算法更佳。