洛谷P1114 “非常男女”计划
洛谷P1114 “非常男女”计划
题目:
题目描述
近来,初一年的XXX小朋友致力于研究班上同学的配对问题(别想太多,仅是舞伴),通过各种推理和实验,他掌握了大量的实战经验。例如,据他观察,身高相近的人似乎比较合得来。
万圣节来临之际,
XXX准备在学校策划一次大型的“非常男女”配对活动。对于这次活动的参与者,XXX有自己独特的选择方式。他希望能选择男女人数相等且身高都很接近的一些人。这种选择方式实现起来很简单。他让学校的所有人按照身高排成一排,然后从中选出连续的若干个人,使得这些人中男女人数相等。为了使活动更热闹,XXX当然希望他能选出的人越多越好。请编写程序告诉他,他最多可以选出多少人来。输入格式
第一行有一个正整数n,代表学校的人数。n≤100000
第二行有n个用空格隔开的数,这些数只能是0或1,其中,0代表一个女生,1代表一个男生
输出格式
输出一个非负整数。这个数表示在输入数据中最长的一段男女人数相等的子序列长度。
如果不存在男女人数相等的子序列,请输出0。
输入输出样例
输入 #1
9 0 1 0 0 0 1 1 0 0输出 #1
6
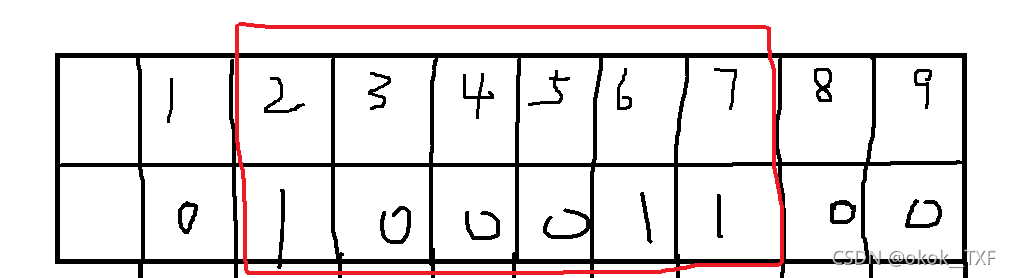
样例解释:男女配对,序列长度必为偶数,下标从1开始,2-7这个序列男女各三人,长度为6
可以得知我们要求的序列中1的个数和0的个数是相等的,那么这个序列所有的0,1加起来刚好就是序列长度的一半。-------->>>>最重要的(也就是区间的和等于区间长度的一半)
序列中的值加起来要怎么求呢? 用for循环一遍一遍地求吗,有那么多子序列,一个一个求肯定会超时的。
这个时候就想起来了求区间和用前缀和数组!!
前缀和数组求区间 [l,r] 和 :prevnum[r] - prevnum[l-1]

然后,枚举所有的区间:
区间长度怎么求?length = j - i + 1
前缀和数组 prevnum[N];
for ( int i = 1; i <= n; ++i ) {
for ( int j = i+1; j <= n; ++j ) {
//判断,我这里就不写了,
//不用想都是超时的,
}
}
//超时
上面说了,序列长度必然为偶数。那么我们的 j 有必要是 逐步加1吗?
是不是完全没必要逐步加1?
当i=1的时候,j=2,3,4,5,6,7…,要使区间长度为偶数,j取2,4,6,8…就行了,
也就是j不是++,而是+=2!!!!
#include <iostream>
using namespace std;
const int N = 1e5+5;
int prevnum[N];
int main()
{
int n, num;
int maxLength = 0;
cin >> n;
for ( int i = 1; i <= n; ++i ) {
cin >> num;
prevnum[i] = prevnum[i-1] + num;
}
for ( int i = 1; i <= n; ++i ) {
for ( int j = i+1; j <= n; j += 2 ) {
if ( (j-i+1)/2 == prevnum[j]-prevnum[i-1] ) {
maxLength = max(maxLength, j-i+1);
}
}
}
cout << maxLength << '\n';
return 0;
}
//然而,还是超时的
再来进一步优化!
再来想,假设我们的 i 在中间,当我们 i 前面的数据更新了maxLength的时候,那个j有必要每次都是i+1开始的吗?j = i+1开始的意思就是每次枚举的时候,都是从长度为2的区间开始枚举的。假如我们i前面的数据更新了maxLength = 4,区间就没有必要从长度2(j=i+1)开始了,直接从4( j = i+manLength-1) 开始就行了。
#include <iostream>
using namespace std;
const int N = 1e5+5;
int prevnum[N];
int main()
{
int n, num;
int maxLength = 0;
cin >> n;
for ( int i = 1; i <= n; ++i ) {
cin >> num;
prevnum[i] = prevnum[i-1] + num;
}
for ( int i = 1; i <= n; ++i ) {
int j;
if ( !maxLength ) j = i+1;//maxLength没有被更新过,就从区间长度2开始
else j = i + maxLength - 1;
for ( ; j <= n; j += 2 ) {
//区间长度的一半 == 区间和
if ( (j-i+1)/2 == prevnum[j]-prevnum[i-1] ) {
maxLength = max(maxLength, j-i+1);
}
}
}
cout << maxLength << '\n';
return 0;
}