LeetCode第245场周赛解题记录

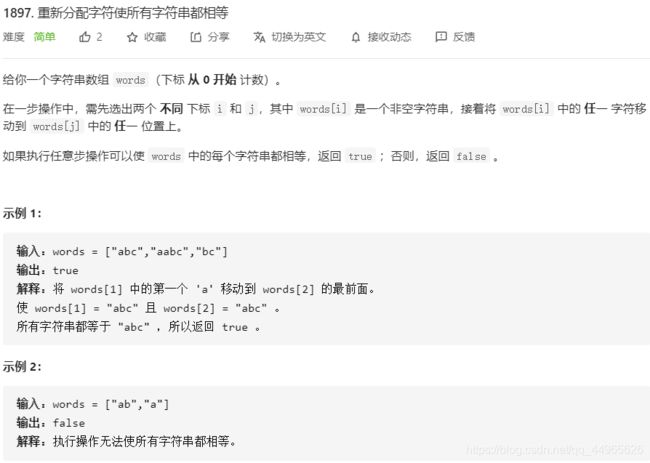
1 1897. 重新分配字符使所有字符串都相等

class Solution {
public:
    bool makeEqual(vector<string>& words) {
        int cnt[26] = {0};
        for(auto word : words)
            for(char c : word)
                cnt[c - 'a']++;
        int n = words.size();
        for(int i = 0; i < 26; i++)
            if(cnt[i] % n != 0)
                return false;
        return true;
    }
};

---

---

---

2 1898. 可移除字符的最大数目

思路：二分+check

1. 在check函数中比较s’和p用了贪心的思想，将s’中最左边的字符与p字符进行配对，然后分别比较s’和p的下一个字符，使得时间复杂度降低为线性。

class Solution {
public:
    vector<int>rem;
    string ss,pp;
    
    bool check(int k)
    {
        string t = ss;
        for(int i = 0; i <= k; i++)
            t[rem[i]] = '3';
        for(int i = 0, j = 0; i < t.size();i++)
        {
            if(t[i] == pp[j])j++;
            if(j == pp.size())return true;
        }
        return false;
    }
    int maximumRemovals(string s, string p, vector<int>& removable) {
        rem = removable;
        int l = 0, r = rem.size() - 1, mid;
        pp = p, ss = s;
        while(l < r)
        {
            mid = l + r + 1 >> 1;
            if(check(mid))l = mid;
            else r = mid - 1;
        }
        if(l == 0 && !check(0))return 0;
        return l + 1;
    }
};

---

---

---

3 1899. 合并若干三元组以形成目标三元组

思路：脑筋急转弯

1. 得到target = [x, y, z]的充分必要条件就是存在满足下列三个条件的一个或多个三元组[a,b,c]：
   1. a=x, b<=y, c<=z
   2. a<=x, b=y, c<=z
   3. a<=x, b<=y, c=z

class Solution {
public:
    bool mergeTriplets(vector<vector<int>>& triplets, vector<int>& target) {
        bool flag1, flag2, flag3;
        flag1 = flag2 = flag3 = false;
        for(auto tr : triplets)
        {
            if(tr[0] == target[0] && tr[1] <= target[1] && tr[2] <= target[2])flag1 = true;
            if(tr[1] == target[1] && tr[0] <= target[0] && tr[2] <= target[2])flag2 = true;
            if(tr[2] == target[2] && tr[0] <= target[0] && tr[1] <= target[1])flag3 = true;
        }
        return flag1 && flag2 && flag3;
    }
};

---

---

---

4 1900. 最佳运动员的比拼回合

思路:DP+记忆化搜索
(建议去看官方题解哈，非常详细，下面代码也是照着官方题解写的)。
补充：

• tie(a, b, c)将变量a,b,c整合成一个tuple,可以实现批量赋值，也可以用于pair变量的解包。

typedef pair<int, int>PII;

class Solution {
public:
    int F[30][30][30], G[30][30][30];
    PII dp(int n, int f, int s)
    {
        if(F[n][f][s])
            return {F[n][f][s], G[n][f][s]};
        if(f + s == n + 1)
            return {1, 1};
        if(f + s > n + 1)
        {
            tie(F[n][f][s], G[n][f][s]) = dp(n, n + 1 - s, n + 1 - f);
            return {F[n][f][s], G[n][f][s]};
        }
        int earlest = INT_MAX, latest = INT_MIN;
        int n_half = (n + 1) / 2;
        if(s <= n_half)
        {
            for(int i = 0; i < f; i++)
                for(int j = 0; j < s - f; j++)
                {
                    auto [x, y] = dp(n_half, i + 1, i + j + 2);
                    earlest = min(earlest, x);
                    latest = max(latest, y);
                }
        }
        else
        {
            int s_prime = n + 1 - s;
            int mid = (n - 2 * s_prime + 1) / 2;
            for(int i = 0; i < f; i++)
                for(int j = 0; j < s_prime - f; j++)
                {
                    auto [x, y] = dp(n_half, i + 1, i + j + mid + 2);
                    earlest = min(earlest, x);
                    latest = max(latest, y);
                }
        }
        return {F[n][f][s] = earlest + 1, G[n][f][s] = latest + 1};
    }

    vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {
        memset(F, 0, sizeof F);
        memset(G, 0, sizeof G);
        if(firstPlayer > secondPlayer)
            swap(firstPlayer, secondPlayer);
        auto[x, y] = dp(n, firstPlayer, secondPlayer);
        return {x, y};
    }
};

---

---

---

参考资料

[1].LeetCode官方题解：最佳运动员的比拼回合
[2].C++函数：std::tie 详解