网格简化 二 、QEM算法

简化算法的误差测度（度量质量和误差）

误差测度用于度量模型简化的质量和误差，因此它对模型的简化过程和最后的简化结果都具有重要的影响。大多数简化算法采用对象空间(Object-space)的一种或综合几种形式的几何误差(Geometric errors)作为误差测度，一些视点相关算法通常将对象空间的误差转换为屏幕空间(Screen-space)的误差值为误差测度，有些算法也考虑模型的颜色、法向量和纹理坐标等属性误差(Attribute errors)。几何误差
几何误差测度一般采用欧式空间距离表示。通常有顶点到顶点、顶点到平面和平面到平面的距离等形式。
Hausdorff距离是现有算法中常常用到度量顶点到表面、表面到表面距离的几何误差测度，该距离为两个模型的顶点之间的最小距离中的最大值。
给定欧式空间的两点集
，Haousdorff距离就是用来衡量这两个点集间的距离。



算法过程：

该算法的时间复杂度是O(n，m)，其中n和m分别为集合A和集合B中的点数。屏幕空间误差计算
视点相关算法常常需要将对象空间误差转换为屏幕空间误差。设对象空间几何误差为e，x为以像素表示的屏幕某方向的分辨率，d是视点到模型对象的距离，θ为视野夹角，则e对应的屏幕空间误差p为：

属性误差（材质、纹理）

网格模型上的三角面片、、法向量、纹理坐标、顶点的颜色是其常见的属性。
网格模型的颜色一般以(r, g, b)三元组形式来表示，各分量分别在[0, 1]中取值。最直接的方法是采用欧式空间距离求解方法来求取颜色的距离。设简化过程的两模型M1、M2的颜色分别表示为(r1, g1, b1)和(r2, g2, b2)，则两模型的颜色距离dc可以表示为：

两个法向量的误差距离dn通常采用角度值进行度量：

多边形表面的纹理坐标用(u, v)坐标对来表示网格模型顶点到二维纹理空间的映射，其中，u，v通常在[0, 1]中取值。一般也是采用欧式空间距离求解方法来计算纹理坐标误差：

简化算法的约束条件或运行条件

模型简化过程中或简化算法运行时往往存在一些限制条件，这些条件也决定了算法采用的技术、算法运行效果和模型简化结构等。细节层次（LOD）
对于各种简化细节层次的LOD模型的管理技术可以分成离散LOD(Discrete LOD)、连续LOD(Continuous LOD)和视点相关LOD技术。
早期简化算法大多采用离散LOD技术。这种技术首先采用离线(offline)方式对原始模型进行预处理，生成一系列不同分辨率的简化模型。在实际运行时，根据需要选择已生成的某个简化模型进行绘制。由于在实时显示绘制时不需要再次进行简化操作，因此该技术具有实时运行速度快、数据存储结构简单等优点。但是因为需要保存多个预处理的中间简化模型，所以占用存储空间大；且在简化预处理时无法考虑视点及实时运行环境因素等要求，只能根据模型本身信息进行简化，因而简化效率不高；同时由于技术限制，预简化生成LOD模型数量不可能过多，粒度不可能太细，因此实时显示绘制时候，在不同简化模型切换过程中会出现画面跳跃、视觉不连续等的效果。离散LOD简化也称为静态简化。
连续LOD技术是对传统的离散LOD技术的改进和发展。与离散LOD技术不同，连续LOD技术的各简化模型不是在预处理中生成，而是通过构造特定的数据结构进行编码存储，在实时显示运行时根据需要生成对应细节层次的简化模型。因此连续LOD技术具有更高的LOD粒度表示，占用空间较小，运行时画面连续性较好等优点；但由于运行时需要进行简化模型的生成处理，因此实时显示速度收到一定影响。连续LOD技术支持多边形网格模型的传输，常被应用于网格模型的各种递进简化算法中。简化模型的拓扑结构保持
简化过程中是否保持网格模型的拓扑结构不变也是区分不同简化算法的一个重要依据。网格模型的拓扑结构通常指构成网格模型的各三角网格之间的连接关系。衡量模型简化算法是否能保持拓扑结构一般是通过判断网格表面的亏格(Genus)和流型(Manifold)是否在简化过程中保持不变来确定。亏格采用网格表面的孔洞数量来计算。
下图为两种类型的顶点对：

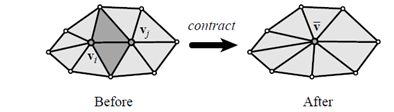
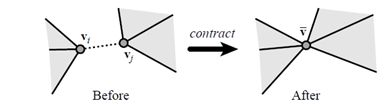
模型试验结果：

QEM算法的基本操作基于边折叠，误差测度采用的是二次误差测度。二次误差测度最早是由Garland提出，采用点到平面距离的平方作为误差测度。它的优点是具有较高的计算速度，较小的内存消耗，而且得到的简化网格具有较高质量。它是在速度非常快但简化质量很差、速度很慢但简化质量非常好的两类方法之间的一种折中，是一种兼顾了速度和质量的较理想的误差测度。
在三维欧氏空间中，一个平面可以表示为： 其中 时平面的单位法向量，d时常量。点 到该平面的距离就可以表示为：

表面属性

在计算机图形学中， 三角网格模型最常见的表面属性有颜色、纹理和法线。为了使简化模型同初始模型具有良好的相似性， 必须在保持模型几何信息的同时保留这些属性特征。由于点到平面的距离考虑了简化操作对顶点周围区域属性值变化的影响， 可以比较准确地描述局部属性误差， 同时又比点到表面或表面到表面的距离计算简便快捷。因此， 采用点到平面的距离作为属性误差测度， 将二次误差测度应用到属性误差的计算中。
网格模型的每个顶点除了空间坐标外，还具有描述其属性的数值。在网格模型的三角面上， 属性值根据几何位置插值得到。因此， 三角面上的属性值是连续的， 而且两个属性值之间的距离用欧氏距离来度量。
比如对于颜色属性，可以用三维矢量r,g,bT 来表示(0≤r,g,b≤1 )，所有颜色矢量构成了RGB彩色空间，在RGB彩色空间中点到平面的距离平方同样可以用二次误差Q(v)来计算。边折叠后的新顶点采用子集选择法，不用重新计算顶点的空间位置和属性值，在计算误差的时候不用考虑空间坐标和属性值的相关性，只需分别建立几何二次误差测度和属性二次误差测度，并计算几何和属性误差。

边折叠操作的代价

采用带有颜色属性的模型应用算法，带有其他属性的网格模型可以同理推出。三角网格模型的每个顶点vg=x,y,zT 和vc=r,g,bT (0≤r,g,b≤1 )来表征几何和颜色信息。为每个三角面建立几何二次误差测度Qfg 和颜色二次误差测度Qfc 。各顶点的二次误差测度之和：

当边折叠(v1 , v2 )到顶点v的时候，总的二次误差测度为：

故而边折叠引起的几何误差Eg=Qgvg ，颜色属性误差Ec=Qcvc 。则总的边折叠代价为：

其中α为颜色属性误差在总代价中的影响系数，可以根据实际情况进行调节

参考资料：

Garland Heckbert. 网格简化算法
网格简化
vcglib库
vcglib库文章
网格简化 QEM 方法详解