代码随想录 LeetCode数组篇 长度最小的子数组
文章目录
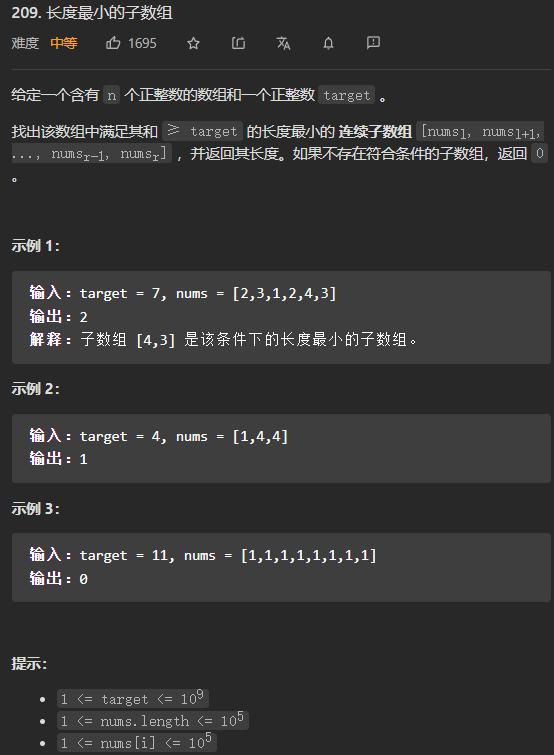
- (中等)209. 长度最小的子数组
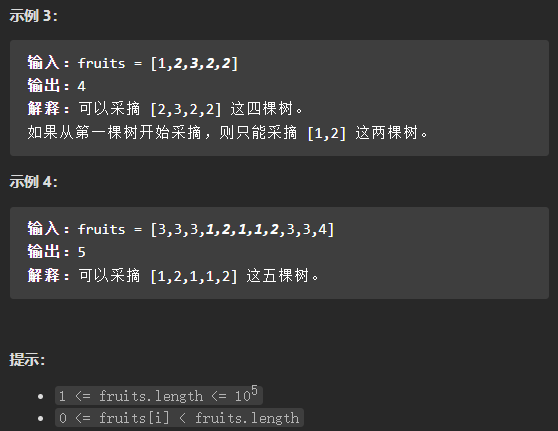
- (中等)904. 水果成篮
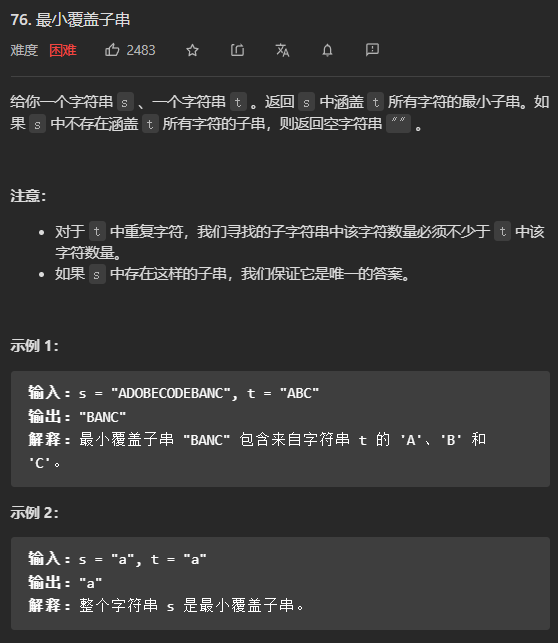
- (困难)76. 最小覆盖子串
(中等)209. 长度最小的子数组
我的思路:双指针p和q,滑动窗口的思想
每次判断从p到q的范围内的值的总和是否大于等于target
- 如果是,那么记录p和q之间的长度,记录p和q的范围内的值的总和,并把p后移一位
- 如果不是,则把q后移一位,扩大区间长度
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int p = 0;
int q = 0;
int sum = 0;
int len = 100001;
int n = nums.length;
while (p < n && q < n) {
if (sum < target) {
sum += nums[q];
q++;
} else {
len = Math.min(len, q - p);
sum -= nums[p];
p++;
}
}
while (p < n) {
if (sum >= target) {
len = Math.min(len, q - p);
sum -= nums[p];
p++;
} else {
break;
}
}
return len != 100001 ? len : 0;
}
}
把代码精简一下
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int n = nums.length;
int len = 100001;
int start = 0;
int end = 0;
int sum = 0;
while (end < n) {
sum += nums[end];
while (sum >= target) {
len = Math.min(len, end - start + 1);
sum -= nums[start];
start++;
}
end++;
}
return len != 100001 ? len : 0;
}
}
官方提供的其他思路,暴力法
暴力法,最直观的方法。初始化子数组的最小长度为无穷大,枚举数据nums中的每个下标为子数组的开始下标,对于每个开始下标i,需要找到大于或等于i的最小下标j,使得从nums[i]到nums[j]的元素和大于等于target,并更新子数组的最小长度(此时子数组的最小长度是j-i+1)
超时
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int n = nums.length;
int len = 100001;
for (int i = 0; i < n; i++) {
int sum = 0;
for (int j = i; j < n; j++) {
sum += nums[j];
if (sum >= target) {
len = Math.min(len, j - i + 1);
}
}
}
return len != 100001 ? len : 0;
}
}
复杂度分析:
-
时间复杂度:O(n^2),其中n是数组的长度。需要遍历每个下标作为子数组的开始下标,对于每个开始的下标,需要遍历其后面的下标得到长度最小的子数组。
-
空间复杂度:O(1)
官方提供的其他思路,前缀和+二分查找
暴力法的时间复杂度是O(n^2),因为在确定每个子数组的开始下标后,找到长度最小的子数组需要O(n)的时间。如果使用二分查找,则可以将时间优化到O(logn)。
为了使用二分查找,需要额外创建一个数组sums用于存储数组nums的前缀和,其中sums[i]表示从nums[0]到nums[i-1]的元素和。得到前缀和之后,对于每个开始下标i,可通过二分查找得到大于或等于i的最小下标bound,使得sums[bound]-sums[i-1]>=target,并更新子数组的最小长度,此时子数组的长度是bound-(i-1)。
因为这道题保证了数组中每个元素都为正,所以前缀和一定是递增的,这一点保证了二分的正确性。如果题目没有说明数组中每个元素都为正,就不能使用二分来查找这个位置了。
import java.util.Arrays;
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int n = nums.length;
int len = 100001;
int[] sums = new int[n + 1];
for (int i = 1; i <= n; i++) {
sums[i] = sums[i - 1] + nums[i - 1];
}
//为了方便计算,令size=n+1
//sums[0]=0,意味着前0个元素的前缀和为0
//sums[1]=A[0],意味着前1个元素的前缀和为A[0]
for (int i = 1; i <= n; i++) {
//得到前缀和以后,对于每个开始下标i,可通过二分查找得到大于或等于i的最小下表bound
//使得sums[bound]-sums[i-1]>=s
int s = target + sums[i - 1];
int bound = Arrays.binarySearch(sums, s);
if (bound < 0) {
bound = -bound - 1;
}
if (bound <= n) {
len = Math.min(len, bound - (i - 1));
}
}
return len != 100001 ? len : 0;
}
}
复杂度分析:
- 时间复杂度:O(nlogn),其中n是数组的长度。需要遍历每个下标作为子数组的开始下标,遍历的时间复杂度是O(n),对于每个开始下标,需要通过二分查找找到长度最小的子数组,二分查找的时间复杂度是O(logn),因此总时间复杂度是O(nlogn)
- 空间复杂度:O(n),其中n是数组的长度。额外创建数组sums存储前缀和。
(中等)904. 水果成篮
我们可以使用滑动窗口解决本题,left和right分别表示满足要求的窗口的左右边界,同时我们使用哈希表存储这个窗口内的数及出现的次数。
我们每次将right移动一个位置,并将fruits[right]加入哈希表。如果,此时哈希表不满足要求(即哈希表中出现超过两个键值对),那么我们需要不断移动left,需要将fruit[left]对应的值减1,当值减少到0时,就需要将fruit[left]为键的元素从哈希表中移除,直到哈希表满足要求为止。
import java.util.HashMap;
class Solution {
public int totalFruit(int[] fruits) {
HashMap<Integer, Integer> map = new HashMap<>();
int n = fruits.length;
int left = 0;
int right = 0;
int ans = 0;
while (right < n) {
map.put(fruits[right], map.getOrDefault(fruits[right], 0) + 1);
while (map.size() > 2) {
map.put(fruits[left], map.get(fruits[left]) - 1);
if (map.get(fruits[left]) == 0) {
map.remove(fruits[left]);
}
left++;
}
ans = Math.max(ans, right - left + 1);
right++;
}
return ans;
}
}
其他思路,也是滑动窗口,使用数组
初始化一个数组,记录每个元素出现的次数
用一个变量来记录当前区间中有几种不同的数字,如果超过两种,则需要移动j(靠左边的指针),来缩小当前窗口,使得窗口中的元素满足题目条件
class Solution {
public int totalFruit(int[] fruits) {
int n = fruits.length;
int[] nums = new int[n];
int total = 0;
int i = 0;
int j = 0;
int ans = 0;
while (i < n) {
nums[fruits[i]]++;
if (nums[fruits[i]] == 1) {
total++;
}
while (total > 2) {
nums[fruits[j]]--;
if (nums[fruits[j]] == 0) {
total--;
}
j++;
}
ans = Math.max(ans, i - j + 1);
i++;
}
return ans;
}
}
(困难)76. 最小覆盖子串
本题要求返回字符串s中包含的字符串t的全部字符的最小出窗口,称包含t的全部字母的窗口为【可行窗口】
使用滑动窗口思想解决这个问题。在滑动窗口类型的问题中,都会包含两个指针,一个用于【延伸】现有窗口的r指针,另一个用于【收缩】窗口的l指针。在任一时刻,只有一个指针在运动,而另一个保持静止。
在s上滑动窗口,通过移动r指针不断扩张窗口,当窗口包含t全部所需的字符后,如果能收缩,我们就收缩窗口直到最小的窗口。
下面的代码是,根据上面的思路,自己写的,因为题目中说明了字符串由英文字母组成,所以用两个长度为52的数组分别记录,在字符串s和t中每个字符出现的次数。前26位存储小写字母出现的次数,后26位存储大写字母出现的次数。
首先,统计字符串t中每个字符出现的次数。
然后遍历字符串s,check()函数用来检验当前left到right的区间内的字符是否已经覆盖了字符串t,就是比较当arrt数组不为零的那些位置,arrs数组中的元素是否大于等于arrt数组中的那些位置,如果相等,则覆盖字符串t。
import java.util.Arrays;
class Solution {
public String minWindow(String s, String t) {
if (s.length() < t.length()) {
return "";
}
int[] arrt = new int[52];
for (char c : t.toCharArray()) {
if (c >= 'a' && c <= 'z') {
arrt[c - 'a']++;
} else {
arrt[c - 'A' + 26]++;
}
}
int[] arrs = new int[52];
int left = 0;
int right = 0;
int l = -1;
int r = -1;
int n = s.length();
int ans = 100001;
while (right < n) {
char rc = s.charAt(right);
if (rc >= 'a' && rc <= 'z') {
arrs[rc - 'a']++;
} else {
arrs[rc - 'A' + 26]++;
}
while (left <= right && check(arrs, arrt)) {
if (right - left + 1 < ans) {
ans = right - left + 1;
l = left;
r = right;
}
char lc = s.charAt(left);
if (lc >= 'a' && lc <= 'z') {
arrs[lc - 'a']--;
} else {
arrs[lc - 'A' + 26]--;
}
left++;
}
right++;
}
return (l == -1 && r == -1) ? "" : s.substring(l, r + 1);
}
public boolean check(int[] arrs, int[] arrt) {
for (int i = 0; i < 52; i++) {
if (arrt[i] != 0) {
if (arrs[i] < arrt[i]) {
return false;
}
}
}
return true;
}
}
下面是官方代码
import java.util.HashMap;
import java.util.Map;
class Solution {
//记录字符串t中每个字符出现的次数
HashMap<Character, Integer> ori = new HashMap<>();
//记录left到right区间内,字符出现的次数
HashMap<Character, Integer> cnt = new HashMap<>();
public String minWindow(String s, String t) {
int tLen = t.length();
int sLen = s.length();
if (tLen > sLen) {
return "";
}
for (char c : t.toCharArray()) {
ori.put(c, ori.getOrDefault(c, 0) + 1);
}
//不断移动的left和right
int l = 0;
int r = 0;
//left,right区间长度
int len = 100001;
//记录当前最优的left和right
int ansL = -1;
int ansR = -1;
while (r < sLen) {
if (ori.containsKey(s.charAt(r))) {
cnt.put(s.charAt(r), cnt.getOrDefault(s.charAt(r), 0) + 1);
}
while (l <= r && check()) {
if (r - l + 1 < len) {
ansL = l;
ansR = r;
len = Math.min(len, r - l + 1);
}
if (ori.containsKey(s.charAt(l))) {
cnt.put(s.charAt(l), cnt.getOrDefault(s.charAt(l), 0) - 1);
}
l++;
}
r++;
}
return ansL == -1 ? "" : s.substring(ansL, ansR + 1);
}
public boolean check() {
for (Map.Entry<Character, Integer> entry : ori.entrySet()) {
Character key = entry.getKey();
Integer value = entry.getValue();
if (cnt.getOrDefault(key, 0) < value) {
return false;
}
}
return true;
}
}