LC买卖股票的最佳时机Ⅱ（三种解法详解）

活动地址：21天学习挑战赛

目录

一、题目描述

 二、解题思路

（1）贪心算法

（2）双指针法

  (3)巧解法

 三、总结

---

一、题目描述

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多只能持有一股股票。你也可以先购买，然后在同一天出售。最后要求返回你能获得的最大利润 。

作者：力扣 (LeetCode)
链接：https://leetcode.cn/leetbook/read/top-interview-questions-easy/x2zsx1/

示例1

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。总利润为 4 + 3 = 7 

示例2

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。总利润为 4 。

示例3

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

 数据规模

• 1 <= prices.length <= 3 * 104
• 0 <= prices[i] <= 104

 二、解题思路

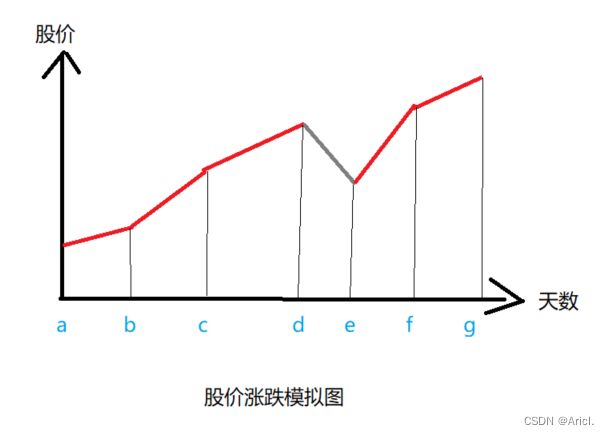
我们以下图为例来示意股票的涨跌情况：

（1）贪心算法

基本思想

贪心算法是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。

通过上图可以发现：当股价持续上涨时，只要不出手手中的股票，等到股价上涨到峰值（拐点）再去抛售股票，此时可以获得该股票上涨区域内的最大利润，后面的情况同理。

这是一种典型的贪心思想，即每次通过获得局部最优解来达到整体最优解。如果股票下跌就不用计算，最终只需要把所有股票上涨的时间段内的利润累加就是我们所要求的结果。

公式法理解：如上图a~d之间股价一直是上涨的，所以a天买入等到d天时候卖出，则此时可以获得的最大利润为(d-a)，这个式子也可以写成（b-a)+(c-b)+(d-c)，即每一个上涨区间的差值累加等于上涨总区间的差值。

解题代码

class Solution {
    public int maxProfit(int[] prices) {
        if(prices==null||prices.length<2){
            return 0;
        }
        int sum=0,index=0,length=prices.length;
        while(index=prices[index+1])
                index++;
            //当上面的循环结束，此时index位于股价开始上涨的位置处，即这段时间上涨的最小值
            int min=prices[index];//记录此时上涨区间内股价的最小值
            //从最小值位置开始，直到找到股价上涨的最大值为止
            while(index

执行结果

（2）双指针法

基本思想

双指针法又称为滑动窗口法，通过设置左右两个指针，指针间距根据具体情况而定，从而形成了类似于一个方形“滑块”从数组的左边向右滑动，每次判断右指针与左指针所对应的记录值进行比较。

解题代码

class Solution {
    public int maxProfit(int[] prices) {
       int left=0,length=prices.length,sum=0;
        for(int right=1;right

执行结果

 

(3)巧解法

看破这道题本质的一位码友说了八个字：求上升区间高度和  言简意赅，一语道破！

解题代码

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        if (n <= 1) return 0;
        int d=0,sum = 0;
        for (int i = 1; i < n; i++) {
            //求相邻元素的差值
            d = prices[i] - prices[i-1];
            //如果差值为正数表面股价上涨，否则为下跌，只需累加上涨区间的差值
            if (d > 0) sum += d;
        }
        return sum;
    }
}

执行结果

 三、总结

上面这道题目算是力扣题中的简单题，但是解法确有很多种，每种算法的性能各有差别。

其实这道题的本质就是要你求一个序列中每个递增区间的差值，然后累加各个差值便是总的最大利润。贪心算法就是这种思想，但双指针法是把区间固定，就是相邻的两天，递增我就累加，否则就跳过。巧解法就看的很透的解法了，直接计算相邻元素的差值，累加正的差值即为所得。

如果把三种解法比喻为人，贪心算法像是一个风险投资者，胆子大，敢于等待后天股票的上涨情况再做打算；而双指针法就像是一个平民百姓初次炒股，只要看到明天股价上涨我就抛售，因为这样是稳赚不赔的，它没有胆量去预测后天的股价情况；那巧解法呢，现实中是赔得血本无归的人。

  

扯远了扯远了，言归正传，我想表达的是刷题其实并不枯燥，要学会在刷题中寻找乐趣！