第三章 栈、队列和数组
第三章 栈、队列、数组
- 栈
-
- 栈的基本概念
- 栈的顺序实现
- 栈的链接实现
- 栈的简单应用和递归
- 队列
-
- 队列的基本概念
- 队列的顺序实现
- 队列的链接实现
- 数组
-
- 数组的逻辑结构和基本运算
- 数组的存储结构
- 矩阵的压缩存储
- 小试牛刀
栈和队列可以看作是特殊的线性表,是运算受限的线性表
栈
栈的基本概念
- 栈是运算受限的线性表,插入和删除运算限定在表的某一端进行,允许进行插入和删除的一端为栈桥顶,另一端为栈底。不含任何数据元素的栈为空栈
- 栈的修改原则是后进先出
栈的顺序实现
- 栈的顺序存储结构是用一组连续的存储单元依次存放栈中的每个元素,并用始端做为栈底

注:进栈操作可以 如下表示:Push(栈名,进栈元素);出栈操作可以如下表示:Pop(栈名,出栈元素)
- 初始化
int InitStack(SeqStk *stk)
{
stk——>top=0;
return 1;
}
- 判栈空
int EmptyStack(SeqStk *stk)
//若栈为空,则返回1,否则返回0
{
if (stk->top==0)
return 1;
else return 0;
}
- 进栈
int Push(SeqStk *stk,DataType x)
{
IF (stk->top==maxsize-1)
{error("栈已满");return 0;}
else { stk->top++; //栈未满,top+1
stk->data[stk->top]=x; //元素x进栈
return 1;
}
}
- 出栈
int Pop(SeqStk *stk)
{
if {EmptyStack(stk)
{error("下溢");return 0;}
else
{
stk->top--;
return 1;
}
}
- 取栈顶元素
DataType GetTop(SeqStk *stk)
{ if(EmptyStack(stk))
return NULLData;
else
return stk->data[stk->top];
}
- 双栈(两个栈头对头放数组两端)
const int max=40;
typedef struct Dbstack
{
DataType data[max];
int top1,top2;
}DbStk;
注:双栈判断上溢为top1+1=top2;判栈空为top1=0时,栈1为空;top2=max-1时栈2为空
栈的链接实现
- 栈的链接实现称为链栈,链栈可以用带头结点的单链表实现,每个结点空间动态分配,不用预先考虑容量大小
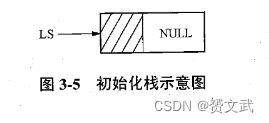
- 初始化
void InitStack(LkStk *LS)
{
LS=(LkStk *)malloc(sizeof(LkStk));
LS->next=Null;
}
- 判栈空
int EmptyStack(LkStk *LS)
//若栈为空则返回值为1,否则返回0
{
if(LS->next==NULL)
retun 1;
else
return 0;
}
- 进栈
void Push(LkStk *LS,DataType x)
{
LkStk *temp;
temp=(LkStk *)mallloc(sizeof(LkStk)); //temp指向申请的新结点
temp->data=x; //新结点的data域赋值为x
temp->next=LS->next; //temp的next域指向原来栈顶结点
LS->next=temp; //指向新的栈顶结点
}
- 出栈
int Pop(LkStk *LS)
//栈顶元素通过参数返回,直接后继成为新栈顶
{
LkStk *temp;
if(!EmptyStack(LS))
{
temp=LS->next; //temp指向栈顶结点
LS->next=temp->next; //原栈顶的下一个结点成为新栈顶
free(temp); //释放原栈顶结点空间
return 1;
}
else rturn 0;
}
- 取栈顶元素
DataType GetTop(LkStk *LS)
{
if (!EmptyStack(LS))
return LS->next->data; //若栈为非空,返回栈顶数据元素
else
return NULLData; //返回空元素
}
栈的简单应用和递归
- 如果在一个函数或数据结构的定义中又应用了它自身,那么这个函数或数据结构称为递归定义的
- 递归定义必须同时满足以下两个条件
- 被定义项在定义中的应用具有更小的“规模”
- 被定义项在最小“规模”上的定义是非递归的
//求3的阶乘
#include队列
队列的基本概念
- 队列是有限个同类型数据元素的线性序列,是一种先进先出的线性表(“排队”)
队列的顺序实现
- 由一个一维数组及两个分别指示队列首和队列尾的变量组成(数组、队列首指针和队列尾指针)
- 类C语言定义顺序队列如下:
const int maxsize=20;
typeof struct seqqueue
{
DataType data[maxsize];
int font,rear;
}SeqQue;
SeqQue SQ;
SQ.rear=SQ.rear+1;
SQ.data[SQ.rear]=x;
出队列操作:
SQ.front=SQ.front+1;
- 循环队列:将存储队列的一维数组首尾相接,形成环状
SQ.rear=(SQ.rear+1)%maxsize;
SQ.data[SQ.rear]=x;
出队列操作为:
SQ.front=(SQ.front+1)%maxsize;
判队列满条件为:
((SQ.rear+1)%maxsize==SQ.front)
判断队列空的条件为:
(SQ.rear==SQ.front)
- 队列的初始化
void InitQueue(CyQue CQ)
{
CQ.front=0;
CQ.front=0;
}
- 判断队列空
int EmptyQueue(CycQue CQ)
{
if(CQ.rear==CQ.front)
return 1;
else
return 0;
}
- 入队列
int EnQueue(CycQue CQ,DataType x)
{
if ((CQ.rear+1)%maxsize==CQ.front)
{error("队列满");return 0;} //队列满,入队列失败
else{
CQ.rear=(CQ.rear+1)%maxsize;
CQ.data[CQ.rear]=x;
return 1;
{
}
- 出队列
int OutQueue(CycQue CQ)
{
if(EmptyqUEUE(CQ))
{error("队列空");return 0;}
else{
CQ.front=(CQ.front+1)%maxsize; //不为空,出队列
return 0;
}
}
- 取 队列首元素
DataType GetHead(CycQue CQ)
{
if (EmptyQueue(CQ))
return NULLData;
else
return CQ.data[(CQ.front+1)%maxsize];
}
队列的链接实现
- 队列的链接实现是使用一个带头结点的单链表来表示队列
- 队列初始化
void InitQueue(LkQue *LQ)
{
LkQueNode *temp;
temp=(LkQueNode *)malloc(sizeof(LkQueNode)); //生成队列的头结点
LQ->front=temp; //队列头指针指向队列头结点
LQ->rear=temp; //尾结点指向列尾结点
(LQ->front)->next=NULL;
}
- 判断队列空
int EmptyQueue(LkQue LQ)
{
if(LQ.rear==LQ.front)
return 1; //队列为空
else
return 0;
}
- 入队列
void EnQueue(LkQue *LQ,DataType x)
{
LkQueNode *temp;
temp=(LkQueNode *)malloc(sizeof(LkQueNode));
temp->data=x;
temp->next=NULL;
(LQ->rear)->next=temp; //新结点入队列
LQ->rear=temp; //置新的队列尾结点
}
- 出队列
OutQueue(LkQue *LQ)
{
LkQueNode *temp;
if(EmptyQueuq(CQ))
{error("队空");retturn 0;}
else{
temp=(LQ->front)->next; //使temp指向队列的首结点
(LQ——>front)——>next=temp->next; //修改头结点的指针域指向新的首结点
if(temp->next=NULL)
LQ->rear=LQ->front;
free(temp);
return 1;
}
}
- 取队列首元素
DataType GetHead(LkQue LQ)
{
LkQueNode *temp;
if(EmptyQueue(CQ))
return NULLData;
else{
temp=LQ.front->next;
return temp->data; //队列非空,返回队列首结点元素
}
}
数组
数组的逻辑结构和基本运算
- 一维数组又称为向量,由一组具有相同类型的数据元素组成,并存储在一组连续的存储单元中。一维数组中的数据元素又是一堆数组结构,则称为二维数组
数组的存储结构
- 一维数组元素的内存单位地址是连续的;二维数组有两种存储方法:以列序为主序的存储、以行序为主序的存储;类C语言编译程序中,采用以行序存储、某些语言编译程序,以列序为主序的存储方式
- 对于二维数组a[m][n],如果每个元素站K个存储元素,以行为主序为例;a[i][j]之前有i行元素,每行n个元素;在第i行有j+1个元素;共计ni+j+1;第一个元素距离a[i][j]相差ni+j个位置
//a[行][列]
a[3][4]
矩阵的压缩存储
- 对称矩阵:若一个n阶方阵A中满足下述条件:
aij=aji 0<=i,j<=n-1

注:设矩阵aij在数组M中位置为k,(i,j)和k存在如下关系:

- 三角矩阵:以主对角线为界的上下半部分是一个固定的值c或零,这样的矩阵叫做上(下)三角矩阵
- 稀疏矩阵:假设m行n列的矩阵有t个非零元素,当t<
- 稀疏矩阵中所有非零元素用三元组的形式表示,并按照一定的次序组织在一起,就形成了三元组表示法

注:v为非零元素,i为非零元素v所在矩阵的行号,j为所在矩阵的列号
小试牛刀
- 栈称为________线性表;队列称为_______线性表
- 设有二维数组int M[10][20],每个元素占2个存储单位,数组的起始地址为2000,元素M[5][10]的存储位置为______,M[8][19]的存储位置为_______
- 对稀疏矩阵进行压缩存储的目的是节省_______
- 一个10X10阶对称数列A,采用行优先顺序压缩存储上三角元素,a00为第一个元素,其存储地址为0,每个元素占用1个存储单元,则a45的地址为______
- 对吸收矩阵进行压缩存储的目的是节省______
- 一个队列的输入序列是1,2,3,4,则队列的输出序列是_______
- 元素进栈次序为A,B,C,D,E,则栈中的出栈顺序可能为_________