matlab第三章笔记

3.1 利用matalb开展线性代数问题

对角矩阵是一种特殊的矩阵，这种矩阵的主对角线元素可以为0或非零元素，而非对角

线元素的值均为0，其创建函数为：A=diag([a1,a2,…,an]);

Matlab提供了函数det(A)来直接求取矩阵A的行列式。如果矩阵A为数值矩阵，则得出

的行列式为数值计算结果，若A定义为符号矩阵，则det()函数将得出解析解。

矩阵的迹的计算公式为对角线上各个元素之和，矩阵A的迹由函数trace(A)求出，并且

trace()函数可以扩展到长方形矩阵的迹计算。

矩阵的秩在线性代数中有三种定义和多种解法，不同的解法，其区别在于部分算法可

能因矩阵的条件数变化而变得不稳定。Matlab提供了rank(A)函数来求解矩阵的秩，其

采用的算法是基于矩阵的奇异值分解的算法进行求解。

矩阵的范数是对矩阵的一种测度。求解矩阵范数的函数norm(A,options)，允许求各种

意义下的矩阵范数，其中参数的选项为1、2、inf和’fro’。

求取矩阵特征多项式系数的函数c=poly(A)

求逆矩阵的函数inv()，其调用格式为C=inv(A)

求取系统特征多项式根的方法由两种，一种方法是通过roots()函数求取系统特征多项式的根；另外一种方法是通过eig()函数直接求取矩阵的特征根。

对于一个线性代数法方程AX=B，其中A和B都是已知矩阵，如何求解矩阵X呢？

唯一解情况：A矩阵为非奇异矩阵，则方程包含唯一解。 求解方法：inv函数。X=inv(A)*B 。

无穷解： 判定矩阵C=[A B] 。如果rank(C)=rank(A)=r基础解系：Z=null(A)。特解：x2=pinv(A)*B。

无解：若上述条件不满足，则说明该方程无解。能利用Moore-Penrose广义逆求解出方程的最小二乘解。 x2=pinv(A)*B。使得原方程中的误差的范围测度最小。

A=[1 2 3 4;2 2 1 1;2 4 6 8;4 4 2 2];
rank(A)
B=[1;3;2;6];
C=[A B];
rank(C)
Z=null(A)
x0=sym(pinv(A))*B
syms a1 a2;
x=Z*[a1;a2]+x0

唯

3.2 利用matlab求解微积分问题

diff()函数来求解导数问题的解析解。

syms t x;
f=t*cos(x)*exp(t*x);
dfdx=diff(f,x)
dfdt2=diff(f,t,2)

syms x;
f=x^2*exp(x);
r1=taylor(f,x,0,'order',6)
r2=taylor(f,x,1,'order',6)

symsum()函数，求解级数求和问题的解析解，symsum(f,k,a,b)，求通式f在指定变量k取遍[a,b]时的和。

积分问题的解析解是通过int()函数来实现的。

matlab中提供了diff()函数和gradient()函数来求解差分问题。

quad函数和integral函数求解数值积分：ss=quad(fun,a,b,tol)

function dy = Example3_14_Fun(t,y)
         dy = zeros(3,1);
         dy(1) = 2 .*y(2) .* y(3);
         dy(2) = -y(1)./ y(3);
         dy(3) = 0.4 .* y(1)^2 .* y(2);

options = odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);
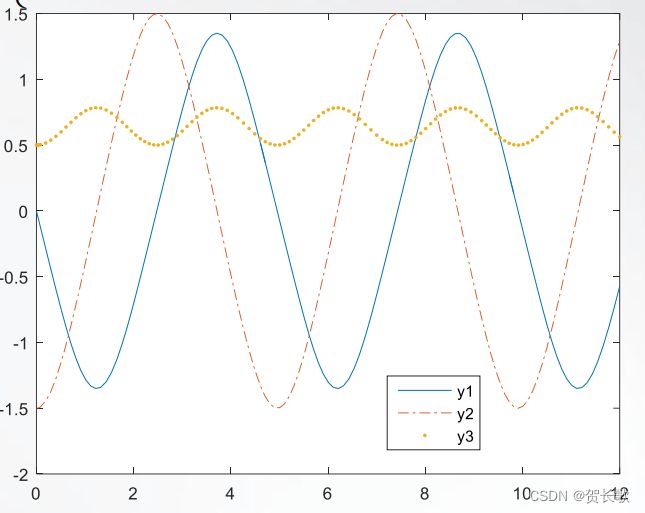
[T,Y] = ode45(@Example3_14_Fun,[0 12],[1 -1.5 0.5],options);
plot(T,Y(:,1),'-',T,Y(:,2),'-.',T,Y(:,3),'.'); legend('y1','y2','y3');

3.3利

3.3用matlab求解优化问题

 

function y = Example3_15_Fun(x)
y = zeros(2,1);
y(1) = exp(exp(x(1)+2*x(2)))-x(1)*x(2)^2;
y(2) = x(1)*cos(x(2))+x(2)*sin(x(1))-1;

x = fsolve(@Example3_15_Fun,[0 0]);

fminbnd()指令函数用于查找单变量函数在固定间隔内的最小值。

fun=@(x)exp(sin(x))*exp(cos(x)+1)*(cos(x)+abs(x));
[xVal,fval,exitflag,output]=fminbnd(fun,-10,10);

 fminsearch()指令函数用于求解无约束条件下，非线性目标函数的局域最小值，并且允许函数为不连续函数。

fun=@(x)15*(2*x(2)-x(1)^2)^2+(1-2*x(1)+x(2))^2;
[xVal,fval,exitflag,output]=fminsearch(fun,[0,0])

 

3.4利用matlab进行插值、拟合和统计

插值是指在离散数据的基础上补插连续函数。是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。