转载于:第十章 使用自组织映射 - 一枚码农
• 自组织映射(SOM)是什么
• 用SOM映射颜色
• 训练SOM
• SOM在森林覆盖率数据中的应用
本章重点介绍用Encog实现自组织映射(SOM)。SOM是一种特殊的神经网络,它对数据进行分类。通常,SOM将映射更高分辨率的数据映射到单维或多维输出。这可以帮助神经网络看到输入数据之间的相似之处。芬兰学院的Teuvo Kohonen博士创建了SOM。正因为如此,SOM有时称为Kohonen神经网络。
Encog提供了两种不同的方法训练SOM网络:
邻域竞争训练
集群复制
这两种训练类型都是无监督的。这意味着不提供理想的数据。简单地给出了网络和数据应该被聚集到的类别的数量。在训练过程中,SOM将对所有训练数据进行聚类。此外,SOM将能够在不重新训练的情况下对新数据进行聚类。
邻域竞争训练法实现了经典的SOM训练模型。SOM训练使用竞争,无监督的训练算法。Encog使用BasicTrainSom类实现这种算法。和以前在本书中使用过相比,这是一种完全不同的训练类型。SOM不使用训练集或计分对象。没有明确定义的目标提供给神经网络。SOM唯一的“目标”是将类似的输入分组在一起。
第二种由encog提供的训练类型是集群复制。这是一种非常简单的训练方法,它只是将权重设置到一个模式里,以加速邻里的竞争训练。这种训练方法也可以用于一个小的训练集,其中训练集元素的数量正好与簇的数量相匹配。集群复制的训练方法是SOMClusterCopyTraining类实现。
本章的第一个示例将颜色作为输入,并将类似的颜色映射在一起。这个GUI示例程序将直观地显示自组织映射如何将相似的颜色组合在一起。自组织映射的输出是拓扑的。此输出通常以n维方式查看。通常,输出是单维的,但也可以是二维的、三维的,甚至是四维的或更高的。这意味着输出神经元的“位置”是重要的。如果两个输出神经元彼此接近,它们将一起训练,而不是两个不那么接近的神经元。
迄今为止,在本书中所研究的所有神经网络都不是拓扑结构。在本书以前的例子中,神经元之间的距离不重要。输出神经元二号对于输出神经元一号和输出神经元数100一样重要。
10.1SOM的结构和训练
一个encog SOM是两层的神经网络实现。SOM简单地有一个输入层和一个输出层。输入层将数据映射到输出层。当模式传入输入层,带有与输入最相似权值的输出神经元被认为是获胜者。
这种相似性是通过比较八组权重和输入神经元之间的欧氏距离来计算的。最短欧氏距离获胜。下一节将讨论欧几里德距离计算。
与前馈神经网络相比,SOM中没有偏置值。相反,只有从输入层到输出层的权重。此外,仅使用线性激活函数。
10.1.1 构建SOM
我们将研究如何构造SOM。这个SOM将被赋予几种颜色来训练。这些颜色将用RGB向量表示。单个红色、绿色和蓝色值可以介于-1和1之间。- 1没有颜色,或黑色,1是完全强度的红色,绿色或蓝色。这三个颜色分量组成神经网络输入。
输出是一个2500个神经元网格,50列50行。这个SOM将在输出网格中组织类似的颜色。图10.1显示了这个输出。
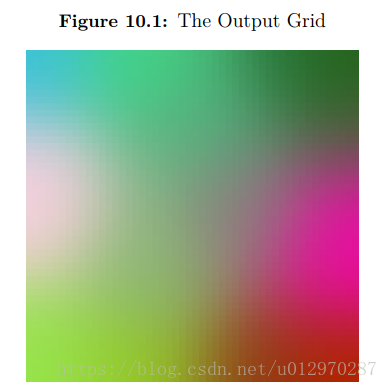
上面的图在本书的黑白版本中可能不太清楚,因为它是彩色的。不过,您可以看到类似的颜色接近对方分组。一个单一基于颜色的SOM是一个非常简单的示例,它允许您可视化SOM的分组功能。
10.1.2 训练SOM
如何训练SOM?训练过程中,将更新3x2500的权重矩阵。将权重矩阵初始化为随机值以开始。然后随机选取15种训练颜色。
就像前面的例子一样,训练将通过一系列迭代来进行。然而,与前馈神经网络不同,SOM网络通常经过一个固定数量的迭代训练。对于本章中的颜色示例,我们将使用1000个迭代。
开始训练我们希望训练的颜色样本,每次迭代选择一个随机颜色样本。选择一个权值最接近基础训练色的输出神经元。训练模式是三个数字的向量。2500个输出神经元和三个输入神经元之间的权值也是三个数的向量。计算权重和训练模式之间的欧氏距离。两者都是三个数的向量。这是用方程10.1完成的。
这与第2章中所示的方程式2.3非常相似。在上述等式中,变量p代表输入模式。变量w表示权向量。通过对各矢量分量之间的差平方和取所得平方的平方根,实现欧氏距离。衡量每个权重向量与输入训练模式的不同程度。
计算每个输出神经元的距离。最短距离的输出神经元被称为最佳匹配单元(BMU)。BMU是从训练模式学的最多的神经元。BMU的邻居学的少些。现在确定了一个BMU,遍历权重矩阵,根据等式10.2更新每一个权重。
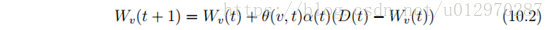
在上述方程中,变量t表示时间,或迭代次数。该方程的目的是计算得到的权重向量WV(T + 1)。接下来的权重会增加当前权重Wv(t)。最终目标是计算当前权重与输入向量的不同。语句D(T)- WV(T)达到此目的。如果我们简单地将这个值添加到权重,权重将正好匹配输入向量。我们不想这样做。我们把它乘以两个比例。以θ表示的第一个比率是邻域函数。第二个比率是单调递减的学习率。
邻域函数考虑我们正训练的输出神经元是多么接近BMU。对于更近的神经元,邻近函数将接近一。对于遥远的邻居,邻域函数将返回零。这就控制了远近邻居如何训练。
我们将在下一节中看看邻域函数是如何确定的。输出神经元将学习学习率还可以缩放多少。这种学习速率类似于反向传播训练中使用的学习速率。然而,随着训练的进展,学习率会下降。
这个学习率必须递减,这意味着函数输出只会随着时间的推移而减少或保持不变。随着时间的增加,函数的输出在任何时间间隔都不会增加。
10.1.3 了解邻域函数
邻域函数决定了每个输出神经元从当前训练模式接受训练的程度。邻域函数将为BMU返回值。这表明它应该接受最多的神经元训练。离BMU较远的神经元将获得较少的训练。邻域函数决定这个百分比。
如果输出仅在一个维度中排列,则应使用一个简单的一维邻域函数。一维自组织映射将输出视为一长串数字。例如,一个一维网络可能有100个输出神经元,这些神经元被简单地看作是一个长的、一维的100个值数组。
一个二维SOM可能采用相同的100个值,并把它们当作网格,可能是10行10列。实际结构保持不变,神经网络有100个输出神经元。唯一的区别是邻域函数。第一种使用一维邻域函数,第二种使用二维邻域函数。函数必须考虑这个附加维度,并将其添加到返回的距离中。
也有可能有三,四,甚至更多的维函数的邻域函数。二维是最流行的选择。一维邻域函数也有点常见。三个或更多维度不经常使用。这实际上取决于计算输出神经元能接近多少种方法。encog支持任何维,虽然每一个额外的维数大大增加了需要的内存和处理能力。
高斯函数是邻域函数的常用选择。高斯函数具有单维和多维形式。单维度高斯函数公式10.3所示。
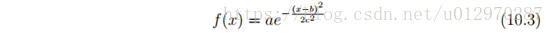
高斯函数的图如图10.2所示。
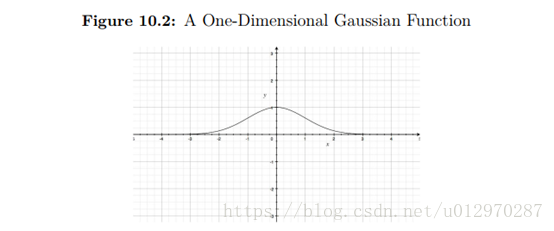
上面的图说明为什么高斯函数是邻域函数的常用选择。如果当前的输出神经元是BMU,那么它的距离(X轴)将为零。因此,训练百分比(y轴)是100%。随着距离的增加,无论是正的还是负的,训练百分比都会降低。一旦距离足够大,训练百分比接近零。
在方程10.3中有几个常数来控制高斯函数的形状。常数a是曲线峰的高度,b是峰的中心位置,c常数是“铃”的宽度。变量x代表当前神经元与BMU的距离。
上述高斯函数只适用于一维输出阵列。如果使用二维输出网格,应使用高斯函数的二维形式。方程式10.4显示了这一点。
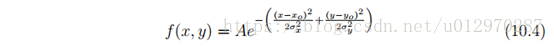
二维高斯函数图像显示如下:

高斯函数的二维形式采用单峰变量,但允许用户为曲线的位置和宽度指定单独的值。这个方程不需要是对称的。
高斯常数如何与神经网络一起使用?尖峰几乎总是一个。为单方面降低训练效果,应将峰值设置在1以下。然而,这更重要的是学习率的作用。中心几乎总是零,使曲线在原点上居中。如果中心发生了改变,那么神经元除了BMU会得到充分的学习。你一般不会这样做。对于多维高斯,将所有的中心设为零以便真正的曲线中心在原点处。
这就留下了高斯函数的宽度。宽度应该设置为略小于网格或数组的整个宽度。宽度应逐渐减小。宽度应像学习速率一样单调递减。
10.1.4 强制一个赢家
对encog SOM竞技训练的一个可选功能是迫使赢家的能力。默认情况下,Encog没有强制一个赢家。但是,这个特性可以用于SOM训练。强迫一个胜利者将尝试确保每个输出神经元至少为一个训练样本获胜。这可能导致优胜者更均匀地分配。然而,它也可以将数据扭曲为某种“工程师”的神经网络。因此,默认情况下它是禁用的。
10.1.5 计算误差
在传播训练中,我们可以通过检测神经网络当前误差来衡量训练的成功。在SOM中没有直接的错误,因为没有预期的输出。然而,这encog接口Train暴露误差特性。此属性确实返回SOM错误的估计值。
误差被定义为“坏的”或与任何BMUs的长距离。随着学习的进展,这个值应该最小化。这就给出了SOM训练的一般近似值。
10.2 使用Encog实现颜色SOM
现在我们将了解如何实现颜色匹配SOM。这个例子有两个类:
MapPanel
SomColors
mappanel类用于显示权重矩阵屏幕。somcolors类扩展JPanel类增加mappanel本身显示。我们将研究这两个类,从mappanel开始。
10.2.1 展示权重矩阵
类mappanel绘制GUI显示SOM的进展。这个相对简单的类可以在下面的位置找到。
convertcolor功能是非常重要的。它将包含1 - 1范围的double转换为RGB分量所需的0到255范围。一个神经网络处理—1到1比0到255要好得多。因此,需要进行这种规范化。

数字128是0和255之间的中点。我们把结果乘以128,使其达到适当的范围,然后从中点加上128。这样可以确保结果在适当的范围内。
使用方法convertcolor绘制方法可以画出SOM的状态。该函数的输出将是所有神经网络权值的颜色映射。2500个输出神经元中的每一个都显示在网格上。它们的颜色取决于输出神经元和三个输入神经元之间的权重。这三个权重被视为RGB颜色分量。convertcolor方法如下所示。

开始通过循环所有行和列。
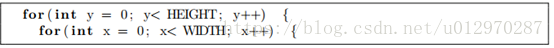
当输出神经元被显示为二维网格时,它们都被存储为一维数组。我们必须从二维的X和Y值计算当前一维位置。

我们从该矩阵中得到三个权重值以及使用convertColor方法转换为RGB组件。

使用这三个组件创建一个新的Color对象。
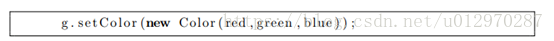
一个填充矩形显示到显示神经元。

一旦循环完成,整个权重矩阵就显示在屏幕上。
10.2.2 训练颜色匹配SOM
应用程序中somcolors类主要作为JPanel使用。它还提供了所有训练的神经网络。可以在以下位置找到此类。
basictrainsom类必须建立以便神经网络训练。为此,需要一个邻域函数。在这个例子中,使用neighborhoodgaussian邻域函数。这个邻域函数可以支持多维高斯邻域函数。下面的代码行创建了这个邻域函数。

这个构造函数创建一个二维高斯邻域函数。前两个参数指定网格的高度和宽度。还有其他构造函数可以创建更高维的高斯函数。此外,还有由encog提供的其他邻域函数。最常见的是neighborhoodrbf。neighborhoodrbf可以使用高斯或其他径向基函数。
下面是邻域函数的完整列表。
NeighborhoodBubble
NeighborhoodRBF
NeighborhoodRBF1D
NeighborhoodSingle
neighborhoodbubble只提供一维邻域函数。指定半径,半径内的任何物体都接受完全的训练。neighborhoodsingle功能作为一个单维邻域函数和只允许BMU接受训练。
neighborhoodrbf类支持几种RBF函数。“墨西哥帽”和“高斯”的RBF是常见的选择。然而,二次函数和逆二次函数也可。
我们还必须创造一个competitivetraining对象利用邻域函数。

第一个参数指定要训练的网络,第二个参数是学习速率。自动将学习速率从最大值降到最小值,因此这里指定的学习速率不重要。第三个参数是训练集。随机给神经网络提供颜色,从而消除了训练集的需要。最后,第四个参数是新创建的邻域函数。
通过后台线程为这个示例提供SOM训练。这使得训练可以在用户观看时进行。后台线程是在run方法中实现的,如下所示。

Run方法开始创建15个随机颜色到训练这个神经网络,这个随机样例将存储在samples lis变量中.

给RGB组件生成随机颜色和随机数字。

以下这行为设置了学习自动衰减的参数速率和半径。
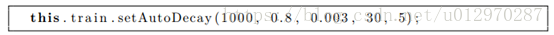
我们必须提供预期的迭代次数。对于这个例子,数量是1000。对于SOM神经网络,有必要知道前面的迭代次数。这与传播训练不同,传播训练或是指定训练时间,或是低于特定错误率。
参数0.8和0.003是开始和结束学习率。每次迭代时,错误率将均匀地从0.8下降到0.003。在最后一次迭代中它应该接近0.003。
同样,参数30和5表示开始和结束半径。半径将从30开始,到最后迭代时将接近5。如果超过计划1000进行迭代,半径和学习率不会低于最小值。

对于每一个竞争学习迭代,有两种选择。首先,你可以选择简单地提供一个mldataset包含训练数据和调用迭代法competitivetraining。
接下来,我们选择一个随机颜色索引并获得该颜色。

trainpattern方法将训练这个随机颜色模式的神经网络。象本章前面介绍的那样,BMU将被确定和更新。

另外,颜色可以被加载到一个mldataset对象和迭代方法可能被使用。然而,在屏幕上显示时,一次使用一个模式并使用一个随机模式看起来更好。
接下来,根据预先指定的参数调用autodecay方法降低学习速度和半径。

重绘。

最后,我们显示关于当前迭代的信息

此过程持续1000次迭代。通过最后的迭代,颜色将被分组。
10.3 总结
直到这一点在书中,所有神经网络都使用监督训练算法,这章介绍无监督训练,无监督训练不提供像反馈神经网络的误差,利率之前的检查。
一种非常常见的神经网络类型,可以在无监督的情况下使用,它是自组织映射(SOM),也被称为Kohonen神经网络,该神经网络仅仅只要输入和输出层,这是一个竞争型的神经网络,神经网被认为最高的输出神经元是获胜神经元。
SOM通过输入模式和输出神经元训练,具有最接近该输入模式的权重值,最接近的匹配神经元,称为最佳匹配单元(BMU),进行训练,所有邻近神经元也训练,该邻近神经元通过邻近函数确定,和邻近训练程度一样,最常用的函数是高斯的变体函数。
这就结束了这本书的Encog编程,Encog是一个不断发展的项目,对当前Encog项目和附加条款的更多信息,访问以下URL:
http://www.encog.org/
Encog非常受到来自用户的反馈,我们很乐意收到你关于Encog需要有哪些有益的新特性的建议。没有软件产品或者书是完美的,Bug报告也很有帮助的,在上面URL有一个论坛,可以用于讨论这本书和Encog。