数据结构之—顺序表和链表
目录
一、线性表的概念
1)线性表存储数据的两种结构/实现方案
2)常见的线性表
二、顺序表
1.概念
2.顺序表的使用
1)创建
2)数组的扩容
3)顺序表的CURD
3.顺序表(动态数组)的特点
三、链表
1.概念
2.单链表
1)创建
2)链表元素的插入
3)链表的查和改
4)链表的删除
5)eg:删除当前链表中所有值为val的节点,返回删除后链表的头节点
6)虚拟头节点
3.链表的特点
4.双向链表
1)创建
2)双向链表的插入
3)双向链表的查和改
4)双向链表的删除
一、线性表的概念
线性表(linear list)是n个具有相同特性的数据元素的有限序列,是一种在实际中广泛使用的数据结构。
1)线性表存储数据的两种结构/实现方案
| 基于数组的线性表 | 顺序表(逻辑+物理连续),又称顺序存储结构 不破坏数据的前后次序,将它们连续存储在内存空间中 |
| 基于链表的线性表 | 链表,又称链式存储结构,元素只是逻辑上连续 所有数据分散存储在内存中,数据之间的逻辑关系全靠“一根线”维系 |
线性表存储时,按逻辑连续存储,呈线性结构,也就说是连续的一条直线。但是在物理结构上并不一定是连续的, 线性表在物理上存储时,通常以数组和链式结构的形式存储。
2)常见的线性表
顺序表、链表、栈、队列、字符串
二、顺序表
1.概念
顺序表(顺序存储结构)是在计算机内存中以数组的形式保存的线性表。线性表的顺序存储是指用一组地址连续的存储单元依次存储线性表中的各个元素、使得线性表中在逻辑结构上相邻的数据元素存储在相邻的物理存储单元中。顺序表是将表中的结点依次存放在计算机内存中一组地址连续的存储单元中。
2.顺序表的使用
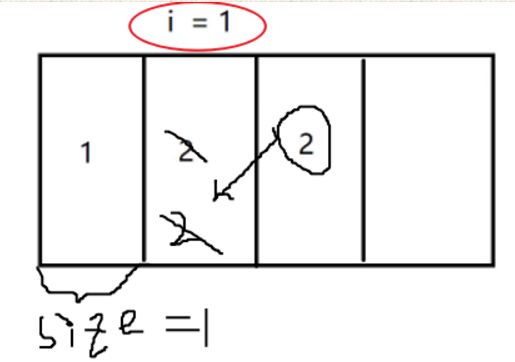
在java中基本的数组是长度固定的,声明后只能存放固定长度的数值(new int[100];)而顺序表是一个动态数组,根据数据的大小动态调整长度(通过扩容操作)。
1)创建
/**
* 基于数组的顺序表
*/
public class DynamicArray {
//存储元素还是在数组中存储,只是套了一层类,从类访问就不用管数组长度固定问题
private int[] data;//定义整型数组
private int size;//当前动态数组中实际存储元素个数
public DynamicArray(){//构造方法
data=new int[10];//将data初始化,默认开辟10个长度的大小
}
public DynamicArray(int capacity){//传容量为capacity
data=new int[capacity];
}
}2)数组的扩容
private void grow() {
//data=Arrays.copyOf(data,data.length<<1);//传入原数组名称和新数组长度【<<1:扩容为原来的1倍】;返回扩容后的新数组
//分开写
int[] newData=Arrays.copyOf(data,data.length<<1);//传入原数组名称和新数组长度【<<1:扩容为原来的1倍】;返回扩容后的新数组
this.data=newData;//类中的data指向扩容后的新数组
}3)顺序表的CURD
1)向index位置插入元素
/**
* 中间位置插入
* @param val
* @param index
*/
public void addIndex(int val,int index){//先判数组是否已满在判断合法性//先给数组扩容在执行合法性判断,否则数组满的情况下插入元素时index>size,插不了
if(size== data.length){
grow();
}
//判断合法性
/**
* 判断index和size的大小关系,不能使用data.length,data.length表示当前数组的最多保存个数,有可能数组的后半部分为空。
* 要使用size属性保证数组的连续性【index>size而不是index>data.length】
*/
if(index<0||index>size){
System.err.println("add index illegal");
return;
}
// if(index==0)addFirst(val);
// else if(index==size)addLast(val);//优化:可以省略,头插尾插也可以当作中间插入
else{//将index位置空出
for (int i = size-1; i >=index ; i--) {
data[i+1]=data[i];
}
data[index]=val;
size++;
}
}
/**
* 遍历打印数组
* @return 向外部返回一个字符串
*/
public String toString(){
String ret="[";
for (int i = 0; i < size; i++) {//不能小于data.length,data.length可能有空,小于size就好
ret+=data[i];
if(i!=size-1){
ret+=",";
}
}
ret+="]";
2)查当前元素是否存在+根据索引查找元素
/**
* 4.在数组中查找val对应的索引下标
* @param val
* @return 返回下标
*/
public int getByValue(int val){
//遍历数组
for (int i = 0; i < size; i++) {
if(data[i]==val){
return i;
}
}
return -1;
}
/**
* 查看当前数组中是否存在val
* @param val
* @return
*/
public boolean contains(int val){
//遍历
for (int i = 0; i < size; i++) {
if(data[i]==val){
return true;
}
}
return false;
}
/**
* 根据索引取得相应位置元素
* @param index
* @return 返回元素值val
*/
public int get(int index){
//判断index合法性
if(index<0||index>=size){
System.err.println("get index iillegal");
return -1;
}
return data[index];
}3)根据索引修改元素
/**
* 将指定元素修改为newValue,返回修改前的元素值
* @param index
* @param newVal
* @return
*/
public int set(int index,int newVal){
if(index<0||index>=size){
System.err.println("set index illegal");
return -1;
}
int oldVal=data[index];
data[index]=newVal;
return oldVal;
}4)删除元素
a.删除指定索引位置元素
/**
* 删除指定索引位置的元素//index+1的元素通过循环依次前移
* @param index
*/
public void removeIndex(int index){
if(index<0||index>=size){
System.err.println("remove index illegal!");
return;
}
for (int i = index; i b.删除数组中第一个值为val的元素
/**
* 删除数组中第一个值为val的元素
* @param val
*/
public void removeValueOnce(int val){
for (int i = 0; i < size; i++) {
if(data[i]==val){
removeIndex(i);
return;
}
}
System.out.println("val不存在");
}c.删除数组中所有值为val的元素
注意:重复元素情况while循环判断并且不能出现i==size的情况,所以还应该有i!=size的条件,当i=size时,会越界,情况如下:
public void removeAllValue(int val){
for (int i = 0; i < size; i++) {
while(i!=size&&data[i]==val){
removeIndex(i);
}
}
}3.顺序表(动态数组)的特点
1)头部增删的时间复杂度:O(N)
每次插入或删除首元素都需要将该元素之后或的元素全部移动一遍。
2)扩容的时间复杂度:O(N),空间复杂度:O(N)
由于顺序表的内存空间是按整块申请,如果需要扩展容量,则必须新开辟一整块新的内存空间。
3)根据索引查找元素的时间复杂度:O(1)【优点】
可以实现随机访问(适合频繁访问的场景),在O(1)时间内找到第i个元素,这是因为顺序表中申请的内存空间是按整块申请,并且每一个元素会有相对应的内存空间数组下标。
4) 顺序表的cpu高速缓存命中率比较高【优点】
三、链表
1.概念
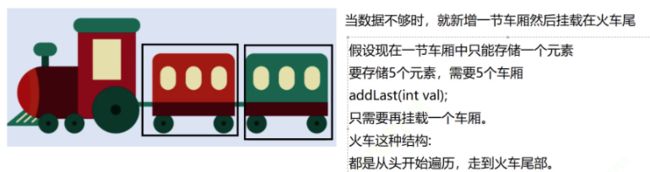
链表是一种物理存储结构上不连续 、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。即逻辑上连续,多个节点采用挂载的方式进行链接,物理上不连续(类比火车):
2.单链表
1)创建
车厢类:具体存储元素的类
class Node{
int data;//具体存储数据
Node next;//存储下一节车厢地址
}火车类:就是由一系列车厢拼起来的
class SingleList{
int size;//当前车厢个数(元素个数)
Node head;//第一节车厢的地址(头节点)
}单链表就是火车类,单链表只能从头部车厢开始遍历,依次走到尾部
/**
* 火车类,是由多个车厢拼接在一起
*/
public class SingleLinkedList {
//当前火车中车厢的节点个数(实际就是具体元素的个数)
private int size;
//当前火车的火车头
private Node head;
}
/**
* 火车车厢类,一个车厢只能保存一个元素
*/
class Node{
//存储具体数据
int val;
//保存下一个车厢的地址
Node next;
public Node(int val){
this.val=val;
}
}2)链表元素的插入
1)头插
插入一个节点,先创建一个车厢:Node node=new Node(val);如果火车为空,当前创建的节点就是头节点,否则不为空时:node.next=head;head=node;(先后顺序不能交换,先把当前车厢的尾部挂载在原先车厢的头部,与原先车厢建立起联系,再把head=node,更新头节点)
/**
* 火车类,是由多个车厢拼接在一起
*/
public class SingleLinkedList {
//当前火车中车厢的节点个数(实际就是具体元素的个数)
private int size;
//当前火车的火车头
private Node head;
/**
* 在火车头部添加元素-添加一个车厢节点
*/
//头插法
public void addFirst(int val){
//新建一个车厢节点
Node node=new Node(val);
//判断当前火车头是否为空
if(head==null){
head=node;
}else{
//火车中有节点,要把当前新车厢挂载到火车头部
node.next=head;
head=node;
}
size++;
}
public String toString(){
String ret="";
//遍历火车这个类/遍历单链表
//从火车头(head)走到火车尾
//暂时存储当前头节点地址(保证head不会受影响)
Node node=head;
while(node!=null){
ret+=node.val;
ret+="->";
//继续访问下一节车厢
node=node.next;
}
ret+="NULL";
return ret;
}
}
/**
* 火车车厢类,一个车厢只能保存一个元素
*/
class Node{
//存储具体数据
int val;
//保存下一个车厢的地址
Node next;
public Node(int val){
this.val=val;
}
}测试:
public class Test {
public static void main(String[] args) {
//使用者用的是火车类
SingleLinkedList singleLinkedList=new SingleLinkedList();
singleLinkedList.addFirst(1);
singleLinkedList.addFirst(3);
singleLinkedList.addFirst(5);
//5->3->1->NULL
System.out.println(singleLinkedList);
}
}2)中间位置插入
首先进行合法性判断,当index<0||index>size是非法的,其次再插入元素:创建节点Node node =new Node(val),node就是待插入元素,插入最核心需要找到待插入位置的前驱节点(起名prev):
a.待插入节点的下一位node.next指向原先前驱节点的下一位prev.next;//node.next=prev.next;.
b.再更新前驱节点的下一位为node;//prev.next=node;
【如何找到前驱,从头结点for循环走index-1步刚好走到前驱(index步走到自己)】
//代码在singleLinkedList的大类下
/**
*单链表任意位置插入元素val
*/
public void addIndex(int index,int val){
if(index<0||index>size){
System.out.println("add index illegal");
return;
}
//⭐⭐这里得加头插法,否则head为空,执行代码会有空指针异常问题
if(index==0){
addFirst(val);
return;
}//⭐⭐
//2.插入元素
Node node=new Node(val);
//找到待插入位置的前驱。默认单链表从头开始,那如何能走着走到前驱-循环
//从头开始走index-1步,刚好找到待插入位置的前驱。
Node prev=head;
for(int i=0;i3)链表的查和改
对于判断合法性,除了添加以外,所有index都不能取到size(改,查,删除时),所以可以将合法性判断抽象成为一个方法:
private boolean rangeCheck(int dex){
if(index<0||index>=size){
return false;
}
return true;
}1)根据index位置取得元素对应值
//返回index位置的元素值
public int get(int index){
if(rangeCheck(int index)){//index合法
//从头结点开始遍历链表,走到index位置
Node node=head;
for(int i=0;i2)查询值为val的元素是否存在
//查询值为val的元素是否在单链表中存在
public boolean contains(int val){
for(Node temp=head;temp!=null;temp=temp.next){
if(temp.val==val){
return true;
}
}
return false;
}3)将单链表中索引为index的值改为newValue,返回修改前的值
//修改index位置的值为newVale
public int set(int index,int newVal){
if(rangeCheck(index)){
Node node=head;
for(int i=0;i4)链表的删除
1)删除链表中index结点
首先判断index合法性,其次考虑边界条件:
a.当index==0时,删除头节点,此时要注意head=head.next的头节点后移操作和head.next=null的断线操作无论哪个先执行都达不到删除目的(原因:先前者此时head指向下一个节点,再执行后者,下一个节点的next置空了,即断了想断的线的后面那根线;先执行后者置空,直接断线,就找不到当前头了),因此,需要引入临时变量存储头节点Node temp=head:
关键步骤:
Node temp=head;
head=head.next;
temp.next=null;
b.index==size-1时,尾节点删除,有前驱,与index节点删除同理
c.删除index节点:找到前驱节点prev,假设待删除节点是cur,需要将cur前后线都断了,并prev.next指向cur.next
关键步骤:
prev.next=cur.next;//这一步指向达到了并且cur前面的线也断了
//(本来前面的线prev.next=cur)
cur.next=null;//断掉cur后面的线
总结:在单链表的插入和删除中,都要找到前驱节点(头节点无前驱,需要特殊处理)
//删除链表中任意结点
public void removeIndex(int index){
if(rangeCheck){//1.判断合法性
//2.删除特殊节点(头节点)情况
if(index==0){
Node temp=head;
head=head.next;
temp.next=null;
size--;
}else{
//index处于中间位置
Node prev=head;//从头开始遍历
for(int i=0;i2)删除链表中值为val的结点
a.遍历链表,找到值为val对应的节点
b.找到后删除【正常删除都需要找到前驱,只有头节点没有前驱】
/*删除第一个值为val的结点*/
public void removeValueOnce(int val){
//遍历链表,找到值为val对应的节点【不知道值为val的节点再哪个位置】
//找到后删除【正常删除都需要找到前驱,只有头节点没有前驱】
//所以先行判断val是否等于头节点存储的值
if(head.val==val){//头节点就是待删除的节点
Node temp=head;
head=head.next;
temp.next=null;
size--;
}else{//head一定不是待删除的节点
Node prev=head;
//判断前驱的下一个节点是否等于val
//⭐看你取值用的是哪个引用,就判断那个引用不为空
while(prev.next!=null){//⭐prev一定不为空,head已经判断过了不是待删除结点
if(prev.next.val==val){//⭐
Node cur=prev.next;//cur就是待删除结点
prev.next=cur.next;
cur.next=null;
size--;
return;
}
//prev不是待删除节点的前驱,prev向后移动
prev=prev.next;
}
}
}/*删除所有值为val的结点*/
public void removeValueAll(int val){
//判断头节点是否为待删除结点
while(head!=null&&head.val==val){
head=head.next;
size--
}
if(head==null){
//此时链表中全是val-待删除
return;
}else{
//此时head一定不是待删除结点,链表中还有节点
Node prev=head;
while(prev.next!=null){
if(prev.next.val==val){
//此时prev.next就是待删除结点
Node cur=prev.next;
prev.next=cur.next;
cur.next=null;
size--;
}
else{//⭐⭐
//prev不是待删除结点的前驱,prev向后走1位
//只有确保prev.next不是待删除节点时,才移动prev指向【保证前驱prev一定不是待删除节点】
prev=prev.next;
}
}
}
}5)eg:删除当前链表中所有值为val的节点,返回删除后链表的头节点
public class Num203{
public ListNode removeElements(ListNode head,int val){
while(head!=null&&head.val==val){
//头节点就是待删除
head=head.next;
size--;
}
if(head==null){
return null;
}else{//此时头节点一定不是待删除结点且链表不为空
ListNode prev=head;
while(prev.next!=null){
if(prev.next.val==val){
// prev.next=prev.next.next
LisrNode cur=prev.next;
prev.next=cur.next;
//不用给cur.next置空,在写题,不用给ListNode置空
}else{//只有prev.next!=val才能执行后移
prev=prev.next;
}
}
}
return head;
}
}
class ListNode{
int val;
ListNode next;
ListNode(){}
ListNode(int val){this.val=val;}
ListNode(int val,ListNode next){this.val=val;this.next=next}
}思路2:递归解决
题目是给定一个头节点为head的链表,就可以删除该链表中所有值为val节点并返回删除后的头节点
方法递归:
1)一个大问题拆分子问题
2)子问题与原问题除了数据大小不同解决思路全一样
3)存在递归出口
已知:head,val
出口:拆到最后一个节点就没了
public ListNode removeElements(ListNode head,int val){
if(head==null){
return null;
}
//将head.next及以后的节点处理不了,交给removeElements(head.next,val)
head.next=removeElements(head.next,val);//head.next更新为删完的链表的头节点
//自己处理下头节点
if(head.val==val){
return head.next;
}
return head;
}6)虚拟头节点
不存在具体值,只是作为链表的头部,此时插入删除元素就可以不需要进行头结点的特殊处理,便于代码的书写。
//带头单链表【虚拟头节点】
public class SingleLinkedListWithHead {
//当前存储的元素个数
private int size;
//虚拟头节点[只作为头部,不存储元素]
private Node DummyHead=new Node(-1);
//⭐⭐
/**
* 1.在index位置插入元素val.此时有虚拟头节点,不用再单独考虑index==0情况
* @param index
* @param val
*/
public void addIndex(int index,int val){
//1.判断合法性
if(index<0||index>size){
System.err.println("add index illegal");
return;
}
//2.所有插入节点全是中间节点【头节点不再是特殊情况了】
Node node=new Node(val);
//找到待插入节点的前驱
Node prev=DummyHead;
for (int i = 0; i < index; i++) {
prev=prev.next;
}
//循环走完prev已经指向了待插入位置的前驱
node.next=prev.next;
prev.next=node;
size++;
}
//头节点插入
public void addFirst(int val){
addIndex(0,val);
}
//尾节点插入
public void addLast(int val){
addIndex(size,val);
}
//⭐⭐
/**
* 删除index节点的元素
* @param index
*/
public void removeIndex(int index){
//1.合法性
if(index<0||index>=size){
System.err.println("remove index illegal");
return;
}
//2.删除中间节点
Node prev=DummyHead;//1)找前驱,从虚拟头节点开始遍历
for (int i = 0; i < index; i++) {//走到前驱位置
prev=prev.next;
}
//2)删除操作
//prev.next=prev.next.next;
Node cur=prev.next;
prev.next=cur.next;
cur.next=null;
size--;
}
/**
* 打印链表
* @return
*/
public String toString(){
Node node=DummyHead.next;
String ret="";
while(node!=null){
ret+=node.val;
ret+="->";
node=node.next;
}
ret+="NULL";
return ret;
}
}
class Node{//车厢类,一个车厢只能保存一个元素
int val;//存储具体数值
Node next;//下一个车厢的地址
public Node(int val){//构造方法-用于赋初值
this.val=val;
}
}3.链表的特点
1)查询的时间复杂度为O(N)
以节点为存储单位,不支持下标的随机访问
2)在任意位置插入删除元素的时间复杂度O(1)
适用于频繁插入删除的场景
3)不用额外开辟过多空间造成空间浪费,用一个结点开辟一个结点即可
按需申请内存,需要存一个数据就申请一块内存,不存在空间浪费
4)缓存命中率低,并且容易造成内存碎片
4.双向链表
又叫双链表,是链表的一种,它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。
在单链表寻找某结点的前驱结点时,必须遍历一遍链表,最坏的时间复杂度 O(n),而双向链表可以直接寻找某结点的前驱结点。
1)创建
class Node{
//指向前驱节点
Node prev;
//保存具体值
int val;
//指向后继节点
Node next;
public Node(int val){
this.val=val;
}
public Node(Node prev,int val,Node next){
this.prev=prev;
this.val=val;
this.next=next;
}
}2)双向链表的插入
1)头插
核心代码:
Node node=new Node(val);
node.next=head;
head.prev=node;
head=node;
优化写法:
Node node=new Node(null,val,head);//核心代码1,2行可以合并成这个
head.prev=node;
head=node;
public void addFirst(int val){
Node node=new Node(null,val,head);
if(head==null){//原先链表为null,插入的元素是第一个元素
//head=node;
tail=node;
}else{
//链表不为null
head.prev=node;
//head=node;
}
//优化:无论head是否为null,head=node,head的值都要更新为node
// 所以可以把两行表达式提出来放在ifelse判断之后这里
head=node;
size++;
}2)尾插
public void addLast(int val){
Node node=new Node(tail,val,null);
if(tail==null){
//tail=node;
head=node;
}else{
//链表不为空
tail.next=node;
//tail=node;
}
tail=node;
size++;
}3)中间位置插入(前驱是prev,插入节点是node)
核心代码:
//后两根线断连
node.next=prev.next;
prev.next.prev=node;
//前两根线断连
node.prev=prev;
prev.next=node;
插入得先遍历找到待插入节点的前驱节点(遍历到index-1位置),而由于CURD都会用到找节点的操作,所以找节点可以抽象成一个方法:
/**
* 找到index索引对应的节点
* @param index
* @return index对应的节点node
*/
private Node node(int index) {
Node ret=null;
//index>1)){
ret=head;
for (int i = 0; i < index; i++) {
ret=ret.next;
}
}else{//此时从后向前遍历
ret=tail;
for (int i = size-1; i >index ; i--) {
ret=ret.next;
}
}
return ret;
} 进行中间位置插入:
public void addIndex(int index,int val){
if(index<0||index>size){
System.err.println("add index illegal");
return;
}else if(index==0){
addFirst(val);
}else if(index==size){
addLast(val);
}else{
//在中间位置插入,找到index的前驱节点
//找节点问题由于CURD都用,可以抽象成一个方法【内部用对外部不可见-private】
Node prev=node(index-1);
//前驱现在找到,开始插入连接四根线
Node newNode=new Node(prev,val,prev.next);//这一步把newNode.prev=prev和newNode.next=prev.next都走了
prev.next.prev=newNode;
prev.next=newNode;
size++;
}
}3)双向链表的查和改
/**
* 3.改-根据索引修改索引位置元素值为newVal,返回未修改之前index位置的元素值
* @param index
* @param newVal
* @return oldVal
*/
public int set(int index,int newVal){
if(rangeIndex(index)){
Node node=node(index);
int oldVal=node.val;
node.val=newVal;
return oldVal;
}else{
System.err.println("set index illegal");
return -1;
}
}
/**
* 2.查找
*/
//找元素是否存在
public boolean contains(int val){
for (Node x=head;x!=null; x=x.next) {
if(x.val==val){
return true;
}
}
return false;
}
//index位置对应元素
public int get(int index){
//index的合法性
if(rangeIndex(index)){
return node(index).val;
}else{
System.err.println("get index illegal");
return -1;
}
}
private boolean rangeIndex(int index) {
if(index<0||index>=size){
return false;
}
return true;
}4)双向链表的删除
所有删除操作都是删除具体节点,所以可以把它抽象成一个方法unlink(Node node)
1)删除一个节点:
/**
*所有删除操作都是删除具体节点,所以可以把它抽象成一个unlink(Node node)方法,删除双向链表中的节点
* 思路:分治,先处理左边判断是否prev空,再看右边判断是否next空
*/
public void unlink(Node node){
Node prev=node.prev;
Node next=node.next;
if(prev==null){
//头节点的删除
head=next;
}else{
prev.next=next;
node.prev=null;
}
if(next==null){
//尾节点的删除
tail=prev;
}else{
next.prev=prev;
node.next=null;
}
size--;
}2)删除index位置节点
//删除index索引位置对应节点
public void removeIndex(int index){
if(rangeIndex(index)){
Node node= node(index);
unlink(node);
}else{
System.err.println("remove index illegal");
return;
}
}
public void removeFirst(){
removeIndex(0);
}
public void removeLast(){
removeIndex(size-1);
}3)删除第一个值为val的节点
public void removeValOnce(int val){
//找到待删除节点
for (Node node=head;node!=null;node=node.next) {
if(node.val==val){
unlink(node);
break;
}
}
}4)删除所有值为val的节点
//删除链表中所有值为val的节点
public void removeValAll(int val){
for(Node node=head;node!=null;){
if(node.val==val){//node是待删除节点
Node temp=node.next;//暂存一下下一个节点的地址
unlink(node);//删除node后node.next为null,得先把下一个结点的地址next暂存一下
node=temp;//把下一节点的地址更新给node
}else{
node=node.next;
}
}
}