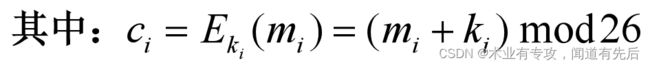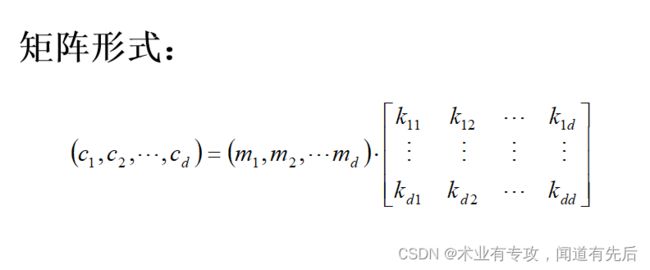第二章——古典密码学及算法实现
凯撒加密
凯撒加密算法实现:
# 凯撒密码加密函数
def caesar_encrypt():
string = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u',
'v', 'w', 'x', 'y', 'z']
# 密文列表
cipher_text_list = []
cipher = int(input("请输入你的密钥:"))
plain_text = input("请输入你的明文:")
length = len(plain_text)
print("加密后的密文是:")
for i in range(0,length):
cipher_text_list.append(string[string.index(plain_text[i])+cipher])
print(cipher_text_list[i],end="")
# 凯撒密码解密函数
def caesar_decrypt():
string = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u',
'v', 'w', 'x', 'y', 'z']
# 明文列表
plain_text_list = []
cipher = int(input("请输入你的密钥:"))
ciphertext = input("请输入你的密文:")
length = len(ciphertext)
print("解密后的明文是:")
for i in range(0,length):
plain_text_list.append(string[string.index(ciphertext[i])-cipher])
print(plain_text_list[i],end="")Playfair密码(流密码)
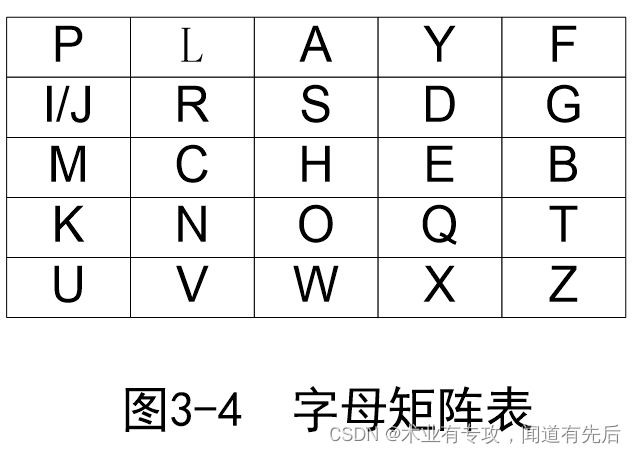
基于一个5×5字母矩阵。
该矩阵使用一个关键词(密钥)来构造。
构造方法:从左至右,从上至下依次填入关键词的字母(去除重复的字母),然后再以字母表顺序依次填入其他的字母。字母I和J被算作一个字母。
原理
P1、P2同行:对应的C1和C2分别是紧靠P1、P2右端的字母。其中第一列被看作是最后一列的右方。(解密时反向)
P1、P2同列:对应的C1和C2分别是紧靠P1、P2下方的字母。其中第一行看作是最后一行的下方。(解密时反向)
P1、P2不同行、不同列:C1和C2是由P1和P2确定的矩形的其它两角的字母,并且C1和P1、C2和P2同行。(解密时处理方法相同)
P1=P2:则插入一个字母于重复字母之间,并用前述方法处理。
若明文字母数为奇数时:则在明文的末端添加某个事先约定的字母作为填充。
Playfair密码—例子
密钥是:PLAYFAIR IS A DIGRAM CIPHER。
如果明文是:P=playfair cipher
明文两个一组: pl ay fa ir ci ph er
对应密文为: LA YF PY RS MR AM CD
Playfair密码的解密
Playfair密码,加密时把字母i和j看作是同一个字符,解密时通过解密时得到明文的意义来区别字母i和j。
Playfair密码的特点:
1.有676(26*26)种双字母组合,因此识别各种双字母组合要困难得多。
2.各个字母组的频率要比单字母呈现出大得多的范围,使得频率分析困难得多。
3.Playfair密码仍然使许多明文语言的结构保存完好,使得密码分析者能够利用。
Playfair加密算法实现:
# Playfair密码
#(创建密钥矩阵的算法小部分参考了其他人的做法,具体加解密核心代码则为原创)
# 字母表
letter_list = 'ABCDEFGHIKLMNOPQRSTUVWXYZ'
# 移除字符串中重复的字母
def remove_duplicates(key):
key = key.upper() # 转成大写字母组成的字符串
_key = ''
for ch in key:
if ch == 'J':
ch = 'I'
if ch in _key:
continue
else:
_key += ch
return _key
# 根据密钥建立密码表
def create_matrix(key):
key = remove_duplicates(key) # 移除密钥中的重复字母
key = key.replace(' ', '') # 去除密钥中的空格
for ch in letter_list: # 根据密钥获取新组合的字母表
if ch not in key:
key += ch
# 密码表
keys = [[i for j in range(5)] for i in range(5)]
for i in range(len(key)): # 将新的字母表里的字母逐个填入密码表中,组成5*5的矩阵
keys[i // 5][i % 5] = key[i] # j用来定位字母表的行
return keys
# 获取字符在密码表中的位置
def get_matrix_index(ch, keys):
for i in range(5):
for j in range(5):
if ch == keys[i][j]:
return i, j # i为行,j为列
def get_ctext(ch1, ch2, keys):
index1 = get_matrix_index(ch1, keys)
index2 = get_matrix_index(ch2, keys)
r1, c1, r2, c2 = index1[0], index1[1], index2[0], index2[1]
if r1 == r2:
ch1 = keys[r1][(c1+1) % 5]
ch2 = keys[r2][(c2+1) % 5]
elif c1 == c2:
ch1 = keys[(r1+1) % 5][c1]
ch2 = keys[(r2+1) % 5][c2]
else:
ch1 = keys[r1][c2]
ch2 = keys[r2][c1]
text = ''
text += ch1
text += ch2
return text
def get_ptext(ch1, ch2, keys):
index1 = get_matrix_index(ch1, keys)
index2 = get_matrix_index(ch2, keys)
r1, c1, r2, c2 = index1[0], index1[1], index2[0], index2[1]
if r1 == r2:
ch1 = keys[r1][(c1-1) % 5]
ch2 = keys[r2][(c2-1) % 5]
elif c1 == c2:
ch1 = keys[(r1-1) % 5][c1]
ch2 = keys[(r2-1) % 5][c2]
else:
ch1 = keys[r1][c2]
ch2 = keys[r2][c1]
text = ''
text += ch1
text += ch2
return text
def playfair_encode(plaintext, key):
plaintext = plaintext.replace(" ", "")
plaintext = plaintext.upper()
plaintext = plaintext.replace("J", "I")
plaintext = list(plaintext)
plaintext.append('#')
plaintext.append('#')
keys = create_matrix(key)
ciphertext = ''
i = 0
while plaintext[i] != '#':
if plaintext[i] == plaintext[i+1]:
plaintext.insert(i+1, 'X')
if plaintext[i+1] == '#':
plaintext[i+1] = 'X'
ciphertext += get_ctext(plaintext[i], plaintext[i+1], keys)
i += 2
return ciphertext
def playfair_decode(ciphertext, key):
keys = create_matrix(key)
i = 0
plaintext = ''
while i < len(ciphertext):
plaintext += get_ptext(ciphertext[i], ciphertext[i+1], keys)
i += 2
_plaintext = ''
_plaintext += plaintext[0]
for i in range(1, len(plaintext)-1):
if plaintext[i] != 'X':
_plaintext += plaintext[i]
elif plaintext[i] == 'X':
if plaintext[i-1] != plaintext[i+1]:
_plaintext += plaintext[i]
_plaintext += plaintext[-1]
_plaintext = _plaintext.lower()
return _plaintext
# plaintext = 'balloon'
# key = 'monarchy'
plaintext = input('明文:')
key = input('密钥:')
ciphertext = playfair_encode(plaintext, key)
print('加密后的密文:' + ciphertext)
plaintext = playfair_decode(ciphertext, key)
print('解密后的明文:' + plaintext)Vigenere密码(流密码)
原理
16世纪法国数学家Blaise de Vigenere于1568年发明的,是著名的多表代替密码的例子
使用一个词组作为密钥,密钥中的每一个字母用来确定一个代替表,每一个密钥字母被用来加密一个明文字母。等所有的密钥字母使用完后,密钥再循环使用.
若明文序列为
密钥序列为:
则密文序列为:
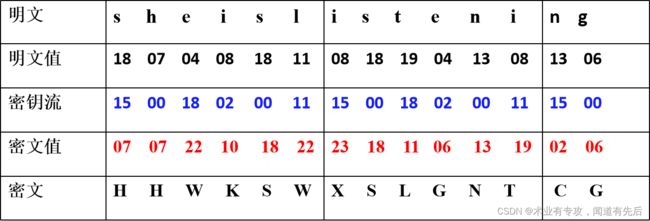
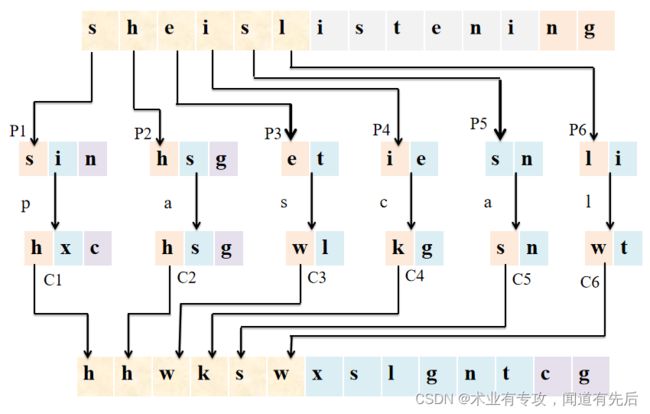
Vigenere密码——例子
明文:She is listening.
密钥:Pascal。
明文:She is listening.
密钥:Pascal。
Vigenere密码可以看做若干个加法密码的联合
Vigenere密码加解密算法实现:
ef VigenereEncrypto(message, key):
msLen = len(message)
keyLen = len(key)
message = message.upper()
key = key.upper()
raw = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"# 明文空间
# 定义加密后的字符串
ciphertext = ""
# 开始加密
for i in range(0, msLen):
# 轮询key的字符
j = i % keyLen
# 判断字符是否为英文字符,不是则直接向后面追加且继续
if message[i] not in raw:
ciphertext += message[i]
continue
encodechr = chr((ord(message[i]) - ord("A") + ord(key[j]) - ord("A")) % 26 + ord("A"))
# 追加字符
ciphertext += encodechr
# 返回加密后的字符串
return ciphertext
if __name__ == "__main__":
message = "Hello, World!"
key = "key"
text = VigenereEncrypto(message, key)
print(text)
def VigenereDecrypto(ciphertext, key):
msLen = len(ciphertext)
keyLen = len(key)
key = key.upper()
raw = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"# 密文空间
plaintext = ""
for i in range(0, msLen):# 开始解密
# 轮询key的字符
j = i % keyLen
# 判断字符是否为英文字符,不是则直接向后面追加且继续
if ciphertext[i] not in raw:
plaintext += ciphertext[i]
continue
decodechr = chr((ord(ciphertext[i]) - ord("A") - ord(key[j]) - ord("A")) % 26 + ord("A"))
# 追加字符
plaintext += decodechr
# 返回加密后的字符串
return plaintext
if __name__=="__main__":
ciphertext = "RIJVS, AMBPB!"
key = "key"
text = VigenereDecrypto(ciphertext, key)
print(text)
import VigenereDecrypto
import VigenereEncrypto
def main():
info = '''==========********=========='''# 开始加密
print(info, "\n------维吉尼亚加密算法------")
print(info)
# 读取测试文本文档
message = open("test.txt","r+").read()
print("读取测试文本文档:test.txt")
print("开始加密!")
# 输入key
key = input("请输入密钥:")
# 进入加密算法
CipherText = VigenereEncrypto.VigenereEncrypto(message, key)
# 写入密文文本文档
C = open("CipherText.txt", "w+")
C.write(CipherText)
C.close()
print("加密后得到的密文是: \n" + CipherText)
# 开始解密
print(info, "\n------维吉尼亚解密算法------")
print(info)
# 读取加密文本文档
print("读取密文文本文档:CipherText.txt")
Ciphertext = open("CipherText.txt", "r+").read()
# 进入解密算法
print("开始解密!")
Plaintext = VigenereDecrypto.VigenereDecrypto(Ciphertext, key)
P = open("PlainText.txt", "w+")
# 写入解密文本文档
P.write(Plaintext)
P.close()
print("解密后得到的明文是 : \n" + Plaintext)
if __name__=="__main__":
main()Hill密码:(分组密码)
原理:
1.输入矩阵K
2.求det(K)取mod 26, 即K1=mod(det(K),26)=25
3.求K1的逆元,即25-1mod26=25
4.求伴随矩阵,K2=inv(K)*det(K)
5.求逆矩阵, K3=K2.*25 (这里K1-1mod26=25)
6.取模 mod(K3,26)
疑问:既然能直接能函数求逆矩阵,那为什么还要用(行列式逆元*伴随矩阵)求逆矩阵呢?
由公式1可以知道求逆矩阵时需要用到行列式逆元,但是公式用的是行列式的倒数(线性代数),所以需要多求一下。
Hill加密算法实现:
# -*- coding: utf-8 -*-
"""
Created on Tue Oct 10 16:09:37 2023
@author: lenovo
"""
import numpy as np
# 求在模m下任意一个数的乘法逆元
def Multi_Inverse(x,m):
# 输入:求一个数x在模m下的乘法逆元
# y的取值范围为[0,m)
y = 0
while(y < m):
res = (x * y) % m
if res == 1:
print("在模%d下,加密密钥行列式值为%d,它的乘法逆元为%d" % (m,x,y))
break
else:
y = y + 1
if y == m:
print(x,"在模",m,"下,不存在乘法逆元!")
return 0
return y
# 求伴随矩阵
def Adjoint_Mat(K,K_det,m):
# 输入:矩阵K,矩阵的行列式值K_det,模m
# 对K矩阵求逆,得到K的逆矩阵K1
K1 = np.linalg.inv(K)
# 求K矩阵的伴随矩阵
K2 = K1 * K_det % m
# 由于伴随矩阵得到的可能是浮点数矩阵,故需要对其进行四舍五入取整
# 并将每个元素成员强制转换为int类型
K2 = np.around(K2)
K2 = K2.astype(np.int)
return K2
# 求解密密钥k
def Decrypt_Key(K,m):
# 求K矩阵的行列式值det(K),模m
K_det = np.linalg.det(K)
K2 = Adjoint_Mat(K, K_det, m)
# 求det(K)在模26下的乘法逆元
y = Multi_Inverse(K_det, m)
# 求Hill加密的解密秘钥
K3 = y * K2 % m
return K3
# 将矩阵(二维数组)ascii码转字符
def ascii2_char(array1):
plaintext = ''
row = array1.shape[0]
col = array1.shape[1]
for i in range(row):
for j in range(col):
plaintext = plaintext + chr(array1[i][j])
return plaintext
# 将明文转换为ascii码值矩阵,行数与加密密钥保持一致
def char2ascii2(plaintext,row,m):
# 输入:明文plaintext,加密矩阵的行数row,模m
l1 = [0,0,0]
l2 = []
for i in range(len(plaintext)):
j = i % row #多少行(一列多少个元素)说明每个分组有多少个元素
if (i > 0 and i % row == 0):
l2.append(l1)
l1 = [0, 0, 0]
l1[j] = ord(plaintext[i])
print('中间变量l1:',l1)
l2.append(l1)
print('中间变量l2:',l2)
m1 = np.array(l2)
# =============================================================================
# np.array()的作用就是把列表转化为数组,也可以说是用来产生数组
# =============================================================================
print('中间变量m1:',m1)
m1 = np.reshape(m1,(m1.shape[1],m1.shape[0]))
# =============================================================================
# reshape函数:将二维数组m1转换成另一个二维数组,形状为(m1.shape[1],m1.shape[0])即(3,10)
# =============================================================================
print('中间变量m1_',m1)
m1 = m1 % m
return m1
if __name__ == "__main__":
# K矩阵,即加密密钥
K = np.array([[17,17,5],[21,18,21],[2,2,19]], dtype=int)
# 解密密钥k,模m
m = 256
k = Decrypt_Key(K,m)
print("Hill密码的解密秘钥为:\n",k)
# 明文
plaintext = 'Programming is a happy thing'
print("原始明文内容:\n",plaintext)
row = K.shape[0] # shape()函数求加密密钥矩阵K的行数row
# 将明文转换为ascii码值矩阵,行数与加密密钥保持一致
# m1为明文ascii码值矩阵
m1 = char2ascii2(plaintext,row,m)
print('明文矩阵:\n',m1)
# 加密过程,m2为加密后的矩阵
m2 = np.dot(K,m1) % 256
# =============================================================================
# 矩阵积计算不遵循交换律,np.dot(a,b)和np.dot(b,a)得到的结果是不同的
# =============================================================================
Ciphertext = ascii2_char(m2)
print("密文内容:\n",Ciphertext)
# 解密过程,m3为加密后的矩阵
m3 = np.dot(k,m2) % 256
decrypt_text = ascii2_char(m3)
print("解密结果:\n", decrypt_text)明文矩阵过程类似下面,但上面代码中明文字符排列顺序为:从左到右,从上到下
下面例子中明文字符排列顺序为:从上到下,从左到右