像计算机科学家一样思考（C++）

像计算机科学家一样思考

计算机科学教最重要的技能就是解决问题

解决问题分为以下3点

1. 明确地表述问题
2. 创造性地思考解决方案
3. 清晰而明确地表达方案

第1章 编程之路

1.1 什么是编程语言

我们要学习的编程语言是C++，因为自1998年起大学先修课程考试就基于C++语言了。之前的考试用的是Pascal语言。C++和Pascal都是高级语言，你或许也听说过Java、C和FORTRAN等其他高级语言吧。

从“高级语言”这个名字可以推断，应该同样存在低级语言，低级语言一般也称为机器语言或汇编语言。不严格地讲，计算机只能执行低级语言编写的程序。正因如此，高级语言编写的程序需要经过翻译才能运行。翻译也要消耗时间，这是高级语言的一个小缺点。

但高级语言的优势是巨大的。首先，使用高级语言编程要容易得多，“容易”意味着编程时间更少，代码更简短易读，出错的可能性更小。其次，高级语言是可移植的，也就是说程序只需要很小的改动甚至不需要改动就可以在各类机器上运行。而低级语言编写的程序只能在某一种机器上运行，必须重写才能支持其他类型的机器。

正因为这些优点，几乎所有的程序都是用高级语言编写的，低级语言仅用于一些特殊的应用场合。

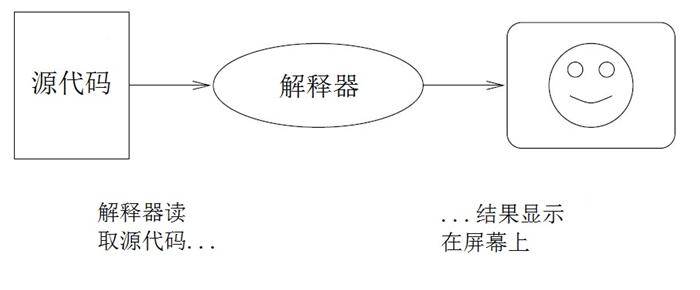
有两种翻译程序的方式：解释 和 编译

。解释器读取高级语言程序并执行程序语句。实际上，解释器采用的是逐行翻译的方式，每读一行就执行该行，然后读取下一行，交替进行。

编译器读取高级语言程序，并在执行程序命令之前全部翻译好。通常，对程序进行编译是独立的一步，之后才能执行编译好的代码。在这种情况下，高级语言程序称为源代码，而翻译后的程序称为目标代码或可执行程序。

比如使用C++编程序时，你可以使用文本编辑器编写代码（文本编辑器是一个简单的字处理器），写好之后，将它保存在一个名为program.cpp的文件中，其中“program”可以是你起的任意名字，而“.cpp”是约定的C++源代码文件后缀。

然后，你可以离开文本编辑器并运行编译器（具体情况取决于你的编程环境）。编译器读入源代码，翻译之后，会创建一个名为program.o的目标代码文件，或者名为program.exe的可执行文件。

编译完成之后，下一步就是执行程序，执行需要某种执行器。执行器负责加载程序（把程序从磁盘复制到内存）并让计算机启动执行程序。

这个过程可能看起来很复杂，但不必担心，大多数编程环境（有时也称作开发环境）已经将这些步骤自动化了。一般而言，你需要做的就是编写代码，然后敲一个命令就能编译和运行程序。另一方面，理解这个过程背后的步骤是有意义的，出错的时候你能更好地找出问题所在。

1.2 什么是程序

程序是说明如何执行一个计算的一组指令序列。计算既可以是数学运算（如求解方程组或者找出多项式的根），也可以是符号运算（如搜索和替换文档中的文本，甚至是编译一个程序）。

不同编程语言中的指令（或者说命令、语句）看起来是不同的，但每种语言都有下面几个基本功能：

输入：从键盘、文件或其他设备获取数据。

输出：在屏幕上显示数据，将数据发送给文件或其他设备。

数学运算：执行基本的数学操作，比如加法和乘法。

测试：检查指定条件并执行相应的语句序列。

重复：重复执行某些动作，但每次执行多少有些变化。

信不信由你，其实就这么多东西。你用过的任何程序，不管多么复杂，都是由上面这些基本功能组合而成的。所以，我们也可以说，编程是将复杂的任务逐步分解为越来越小的子任务，直到子任务简单到可以用上面某个基本功能来执行为止。

1.3 什么是调试

编程是个复杂的过程，而且因为由人来完成，所以难免出现错误。由于一些特殊的原因，编程错误称为“bug”，而跟踪和修正错误的过程称为“debugging”，中文叫做调试。

程序中会出现几种不同类型的错误，分清这几类错误有助于快速找出问题。

1.3.1 编译时错误

编译器只能翻译语法正确的程序，当存在语法问题时，编译失败，你也就无从运行程序了。语法指程序的结构和结构的规则。

例如，英语中的句子必须以大写字母开头并以句号结尾。不以大写字母开头或者不以句号结尾的句子在语法上都是错误的。

对大多数读者而言，语法错误不是个严重问题，我们读e e cummings的诗歌时并不会感觉到很多语法错误就是这个原因。

编译器可没这么宽容。程序中不管哪里出现了一个语法错误，编译器都会打印错误信息并退出，结果就是没办法执行程序。

更麻烦的是，C++中的语法规则比英语要多得多，而且编译器给出的错误提示信息不见得总有用。在我们刚学着编程的前几周，你可能要花很多时间来查找语法错误。随着经验的增长，你犯的错会越来越少，找出错误也会更快。

1.3.2 运行时错误

第二类错误是运行时错误，因为这类错误在程序运行时才会出现。

下面几周我们编写的都是很简单的程序，运行时错误非常少见，可能过一段时间才会遇到。

1.3.3 逻辑与语义错误

第三类错误是逻辑或语义错误。如果程序中有逻辑错误，程序仍会正确编译并运行，编译器不会生成任何错误消息，但是程序运行得不到预期结果。程序执行的不是你需要的功能。其实，你让程序做什么它就做什么，问题在于，你写出的代码和你本来要设计的功能并不一致。也就是说，程序的语义错了。识别逻辑错误可能很复杂，因为这需要你根据程序的输出和找出程序到底在做什么来倒推问题所在。

1.3.4 实验性调试

调试应该是你能从本书中学到的最重要的一个技能。虽然调试过程中可能有挫败感，但调试是编程中最具智慧、挑战和乐趣的部分之一。

从某种角度看，调试就像侦探工作。你要根据线索来推理各种过程和事件，最终找到结果。

调试又像做实验。一旦意识到出了问题，你就要修改程序并重新尝试。如果所做的假设正确，你就能预测对修改后的结果，这就离正确的程序又近了一步。如果假设错误，你就要提出新的假设。就像夏洛克•福尔摩斯所说的，“排除了那些不可能的之后，无论剩下什么，即使再不可思议，也一定是真相”（出自柯南道尔的《四签名》一书）。

对某些人而言，编程和调试是一回事。编程就是逐步调试程序直到它满足要求为止。这其中的理念是，总是从一个实现部分功能、可以工作的程序开始，然后加以小的改进并随手调试通过，这样保证总是有一个可用的程序。

比如Linux，它是个包含成千上万行代码的操作系统，最开始却是Linus Torvalds为探索Intel 80386芯片的功能而开发的一个简单程序。据Larry Greenfield所说，“Linus Torvalds早期有个项目，是交替打印AAAA和BBBB的程序，这个程序后来发展为了Linux”（出自The Linux Users’ Guide Beta版1）。

后续章节会有更多有关调试和其他编程实践的建议。

1.4 形式语言与自然语言

自然语言是人类讲话使用的语言，如英语、西班牙语和法语等。虽然人们总要给自然语言加上一些规则，但自然语言并非人类设计，它们是自然演化而来的。

形式语言是人们为特定应用设计的语言。例如，数学家使用的记号就是一种便于表示数字与符号关系的形式语言。化学家也使用一种形式语言来表示分子的化学结构。最重要的是：

编程语言是人为设计的用来表达计算的形式语言。

前面也提到过，形式语言有严格的语法规则。比如3+3=6是符合语法的数学语句，而3=+6$则不是。同样H2O是符合语法的化学式，但2Zz不是。

这里的两个2都是下标，在Markdown语法中无法表示。下段同。——译者注

语法规则包含两个方面：标识符与结构。标识符是语言的基本元素，像单词、数字以及化学元素等。3=+6$的一个错误是，至少据我所知$不是数学上合法的标识符。类似的，2Zz也是非法的，因为没有缩写为Zz的化学元素。

第二种语法错误是句子结构上的，即标识符的排列方式。语句3=+6$结构上也是非法的，因为加号不能直接放在等号后面。类似地，化学式中的下标必须在元素名后面，而不能在前面。

阅读英语的句子或者形式语言的语句时，必须分析句子结构（使用自然语言时，你会下意识地这样处理）。这个过程叫做解析。

例如，当你听到“The other shoe fell”这句话时，你会知道“the other shoe”是主语而“fell”是动词。分析完句子结构，你就理解了它的意思，即句子的语义。假设你知道“shoe”是什么，也知道“fall”的意义，你就能理解句子的大体含义。

虽然形式语言和自然语言有很多共同点，如标识符、结构、语法和语义，但是它们仍然有很多不同点：

歧义：自然语言常有歧义，人们需要根据上下文和其他信息来理解。而形式语言天生就是清晰无二义的，也就是说不管上下文是什么，任何语句都有一个精确的意义。

冗余：为了弥补歧义问题并减少误解，自然语言引入了很多冗余，结果就是语言常常很冗长。形式语言冗余少些，更加简洁。

字面意义：自然语言有很多成语和隐喻。比如我说“The other shoe fell”，可能不是说鞋，也没有什么东西掉下来。而形式语言语句的含义和字面意义是完全一致的。

说着自然语言长大的我们，通常都要经历一段痛苦的时期才能适应形式语言。从某些方面来说，自然语言和形式语言的差别就像诗歌和散文的差别，而且可能还有过之无不及：

诗歌：选词既要求发音，又要求含义，整首诗营造出一种效果或情感响应。歧义不仅常见，很多时候是有意为之。

散文：词汇的字面意思更加重要，而且句子结构也更能表意。相对于诗歌，散文更经得起推敲，但仍然会存在歧义。

程序：计算机程序的含义是无歧义的，和语句的字面意思一致，通过对标识符和结构的分析可以完整地理解。

关于阅读程序（或其他形式语言）提几点建议：首先，形式语言比自然语言难懂得多，所以读起来会花费更长的时间。其次，结构非常重要，从上到下、从左到右地阅读并不见得管用。相反，要学会在头脑中分析程序，识别标识符并解读清楚句子结构。最后，细节很重要，像拼写或者标点符号错误，在自然语言中有可能无伤大雅，但在形式语言中可能造成天壤之别。

1.5 第一个程序

习惯上，人们学习一门新语言时写的第一个程序都是“Hello,World.”，它只是输出“Hello,World.”这句话。下面是C++版本1：

#include 

// main: 生成一些简单的输出

void main ()
{
    cout << "Hello, world." << endl;
    return 0
}

有些人喜欢通过“Hello,World.”程序是否简洁来判断编程语言的质量。如果以此为标准，C++相当不错。即便如此简洁，这个程序中还是有几个特性不容易给初学者解释清楚。我们暂且忽略这种不易理解的特性，比如第一行的#include语句。

第二行以“//”开始，它表明这句话是注释。注释是可以放入程序中的英语文本，用以解释程序的意图。当编译器读取到“//”时，会忽略从“//”开始直到行尾的所有字符。

在第三行中，你暂时先别理会单词void，但要注意另一个单词main。main是一个特殊的名字，它指明程序开始执行的位置。程序运行时，会从main中的第一条语句开始执行，然后按顺序执行后续语句，直到最后一条语句，最后退出。

main中的语句行数并没有限制，不过例子中只包含了一条语句。这是一条基本输出语句，会在屏幕上输出或者显示一条信息。

cout是系统提供的特殊对象，允许将输出发送给屏幕。符号<<是应用到cout和一个字符串上的操作符，它在屏幕上显示这个字符串。

endl是表示一行结束的特殊符号。当把endl发送给cout时，会导致光标移到显示的下一行。下一次输出时，文本会出现在新行上。

和所有语句一样，输出语句也以分号结尾。

程序中的语法有几点需要注意。首先，C++使用花括号组织语句。示例程序中，输出语句被包围在花括号之中，说明它在 main函数定义之内。再有，注意语句的缩进，这可以更直观地表示出哪些语句在定义之内。

现在，何不坐到电脑前面编译并运行这个程序？具体如何编译运行与你的编程环境有关，从现在开始，本书假设读者了解该如何处理。

前面也提到过，C++编译器对语法细节要求十分严格。编写程序时出现任何错误，代码都无法成功编译。比如，若把iostream拼写错了，你可能会遇到下面的错误提示信息：

hello.cpp:1: oistream.h: No such file or directory

虽然这行提示包含了大量信息，但这种信息密集的说法着实不易理解。更友好的编译器可能要这样说：

“在名为`hello.cpp`的源代码文件的第一行，你想要包含一个名为`oistream.h`的头文件。我没有找到叫这个名字的文件，但我找到了`iostream.h`，也许这是你要找的文件？”

十分不幸，几乎没有这么友好的编译器。编译器并不是真的非常聪明，大多数情况下，错误信息只是程序错误的一个线索。要熟练理解编译器的信息还是需要些时间磨练的。

不过，编译器仍然是学习语言的语法规则的有用工具。拿一个可以工作的程序(如hello.cpp)练手，以各种方式修改它，看看会发生什么。如果碰到错误信息，记住消息说了什么以及是什么原因导致的错误，下次再遇到的时候就知道错误信息的意义了。

1.按照C++规范，返回值应为int类型，但本书第5章才会介绍有返回值的函数，这里暂且用void，第5.9节会有相关说明。——译者注

1.6 术语表

解决问题（problem-solving）：提取问题、寻找方案、表达方案的过程。

高级语言（high-level language）：为了人们能够方便地读写而设计的编程语言，如C++。

低级语言（low-level language）：为了便于计算机执行而设计的编程语言。也称作“机器语言”或“汇编语言”。

可移植性（portability）：程序可以在多种平台上执行的属性。

形式语言（formal language）：人们为特定目标而设计的语言，比如为了表示数学思想或计算机程序而分别设计的语言。所有编程语言都是形式语言。

自然语言（natural language）：自然而然发展起来的、人类说话用的语言。

解释（interpret）：通过逐行翻译的方式执行高级语言程序。

编译（compile）：一次性将高级语言编写的程序翻译为低级语言程序，为随后的执行做好准备。

源代码（source code）：高级语言编写的、未经编译的程序。

目标代码（object code）：编译器翻译程序后输出的代码。

可执行程序（executable）：可以立即执行的目标代码的别名。

算法（algorithm）：解决某类问题的一般过程。

bug：程序中的错误。

语法（syntax）：程序的结构。

语义（semantics）：程序的含义。

解析（parse）：检查程序并分析其语法结构。

语法错误（syntax error）：导致程序无法解析(也就无法编译)的错误。

运行时错误（run-time error）：导致程序在运行时失效的错误。

逻辑错误（logical error）：导致程序没有按照编程者意图执行的错误。

调试（debugging）：找到并解决语法错误、运行时错误或逻辑错误的过程。

第2章 变量和类型

2.1 更多的输出

上一章提到，可以在main函数中写任意多的语句。例如，输出超过一行：

#include 

//main: 生成一些简单的输出

void main()
{
    cout << "Hello, world." << endl;        //输出一行
    cout << "How are you?" << endl;         //输出另一行
}

可以看到，在一行的结尾处写注释与在独立的某行写注释一样，都是合法的。

引号中的内容被称为字符串，因为它们是由一个字母序列组成。事实上，字符串可以包含任何字母、数字、标点符号以及其他特殊字符。

有时想把多个输出语句的内容显示在一行上。这时只要去掉第一个endl即可：

void main()
{
   cout << "Goodbye, "
   cout << "cruel world!" << endl;
}

这时，输出内容会出现在一行中，变成Goodbye, cruel world!。注意到单词Goodbye,和右引号之间有一个空格。这个空格出现在输出中，因而它影响了程序的行为。

引号外面的空格通常不会影响程序的行为，例如，我可以这么写：

void  main()
{
	cout<< "Goodbye, ";
	cout<< "cruel world!"<<endl;
}

这段程序可以像原来那段程序一样编译和运行。行尾的的空格（新行）并没有影响到程序运行的结果，因此我也可以这么写：

void main(){cout<<"Goodbye, ";cout<<"cruel world!"<<endl;}

同样有效，但是你可能已经发现，这样下去程序会越来越难读。换行符和空格是很有用的元素，可以把程序组织得更直观，使程序更易读，也更易于定位语法错误。

2.2 值

值是程序处理的基本元素，就像字母或数字一样。到目前为止，我们只操作过字符串类型的值，像"Hello, world."。你（以及编译器）能识别出字符串值是因为它们被引号括起来了。

此外，还存在其他类型的值，包括整型和字符型，整型值就是一个整数，类似1或17。你可以用输出字符串的方式输出整型值：

cout << 17 << endl;

字符值是使用单引号括起来的一个字母、数字或标点符号，类似‘a’或者‘5’。你可以用同样的方法输出字符值：

cout << '}' << endl;

这个例子输出了一个大括号。

不同类型的值之间很容易混淆，像“5”、'5'和5。但如果你注意标点符号的话，可以清楚地分辨出第一个是字符串，第二个是字符，最后一个是整型。你很快就会明白这种区分为什么如此重要。

2.3 变量

程序设计语言最强大的一个特性是能对变量进行操作。变量是存放值的一个位置，我们给这个位置赋予了名字。创建一个变量时，你应该先声明它的类型。例如，C++中字符类型被称为char。以下语句创建了一个名为fred的新变量，类型为char。

char fred;

这种类型的语句被称为声明语句。

变量的类型决定了它能存储何种值。char类型的变量可以包含字符串，自然，int变量可以存储整数。

C++中有几种类型可以存储字符串值，但这里我们先不说它（第七章再讨论这个话题）。

创建一个整型变量的语法如下：

int bob;

bob是你为变量取的任意一个名字。一般来说，你为变量取的名字会反映这个变量的用途。例如，看到以下变量声明：

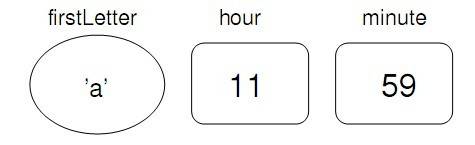
char firstLetter;
char lastLetter;
int hour, minute;

你很可能会猜测到它们存储什么值。这个例子同样展示了可以使用同一个类型声明多个变量：hour和minute都是整型（int 类型）。

2.4 赋值

上面已经创建了一些变量，我们想用它们存一些值，可以通过赋值语句来实现。

firstLetter = 'a';    // give firstLetter the value 'a'
hour = 11;           // assign the value 11 to hour
minute = 59;        // set minute to 59

这个例子展示了三个赋值语句，注释则展现了人们谈及赋值语句的三种不同说法。这里用到的词汇可能有些让人疑惑，但是想法很直接：

• 声明一个变量时，你是创建了一个有名字的存储位置。
• 对一个变量赋值时，你是给了它一个值。

在纸上展示变量的一种常用方式是画一个框，变量名在外，变量值在内。这种图被称为状态图，因为它展示了每个变量所处的状态（你可以把它想成变量的“精神状态”）。下图展示了以上三条赋值语句的作用：

有时候我会使用不同的形状来区分不同的变量类型。这些形状应该帮助你回想起C++中的一个规则，即一个变量应该和你分配给它的变量值的类型相同。例如，你不能把一个字符串存储到一个int类型的变量中。以下语句会产生编译错误：

int hour;
hour = "Hello.";       // WRONG !!

这条规则有时候会引起混乱，因为你经常会把值从一种类型转换成另一种类型，而且C++有时候会自动转换。但是现在你应该记住它，把它当做基本规则：变量和值应该具有相同的类型。我们之后会讨论特殊情况。

另一个易让人混淆的是一些字符串看起来像整型，实际上却不是。例如，字符串“123”，它由字符1，2，3组成，和数字123是不同的，以下语句是非法的：

minute = "59";  //   错误！

2.5 输出变量

我们之前用了一些指令输出简单的值，你也可以使用相同的指令来输出一个变量的值。

int hour, minute;
char colon;

hour = 11;
minute = 59;
colon = ':';

cout << "The current time is";
cout << hour;
cour << colon;
cout << minute;
cout << endl;

这段程序创建了两个整型变量，名为hour和minute，以及一个名为colon的字符变量。它给每个变量赋予了合适的值，然后使用一系列输出语句来生成以下内容：

The current time is 11:59

我们说“输出一个变量”，指的是输出这个变量的值。要输出变量的名称，需要把它的名称放在引号中，如：

cout << "hour";

像前面看的那段程序，你可以在一个输出语句中包含多个值，使程序更加简洁：

int hour,minute;
char colon;

hour = 11;
minute = 59;
colon = ':';

cout << "The current time is " << hour << colon << minute << endl;

在一行中，这段程序输出了一个字符串、两个整型数、一个字符以及一个特殊值endl。非常棒！

2.6 关键字

前几节我曾经说过你可以为变量取任意名字，但是这并不完全正确。C++中有一些特定的词是被保留的，它们由编译器使用，用于分析你程序的结构。如果你用它们作为变量名称，会造成混乱。这些词被称为关键字，包括int、char、void、endl等。

全部的关键字在《C++标准》中列出，《C++标准》是1998年9月1日被国际标准化组织所采用的官方语言定义。你可以从以下网址下载一份电子版：

https://isocpp.org/

你不需要记住这个列表，我建议你利用许多开发环境都提供的代码高亮功能。一旦你输入内容，程序的不同部分会呈现不同的颜色。例如，关键字可能是蓝色的，字符串是红色的，其他代码是黑色的。如果你输入的一个变量名变成了蓝色，要小心了！你可能会使编译器产生一些诡异行为。

2.7 操作符

操作符是特别的符号，用于表示简单的计算，比如加法和乘法。C++中大部分的操作符都会按照你所期望的去做，因为它们都是常用的数学符号。例如，用于两个整数相加使用的操作符是+。

以下都是合法的c++表达式，它们的含义几乎都是很明显的：

1+1       hour-1        hour*60 + minute       minute/60

表达式可以同时包含变量名和整型值。在所有情况下，变量在计算之前都会被它所代表的变量值所替代。

加法、减法和乘法都和你预期的相同，但是你可能会对除法感到奇怪，例如以下程序：

int hour,minute;
hour = 11;
minute = 59;
cout << "Number of minutes since midnight: ";
cout << hour*60 + minute << endl;
cout << "Fraction of the hour that has passed: ";
cout << minute/60 << endl;

这段程序会得到以下输出：

Number of minutes since midnight: 719
Fraction of the hour that has passed:0

第一行是我们所预料的结果，但是第二行有些奇怪。变量minute的值是59,59被60除得到0.98333，而不是0。产生这种差异的原因在于C++采用的是整型除法。

当两个操作数都是整数时（操作数即操作符操作的对象），结果必须同样是整数，定义整数除法总是向下圆整，即便结果与上面一个整数更接近。

cout << "Percentage of the hour that has passed: ";
cout << minute*100/60 << endl;

结果是：

Percentage of the hour that has passed: 98

结果再一次被向下取整，但至少现在答案是近似正确的。为了得到一个更精确的答案，我们可以使用另外一种变量类型，称为浮点型，它可以存储浮点数。下一章我们会讨论它。

2.8 操作顺序

当表达式中出现了多个运算符的时候，计算顺序取决于优先级规则。一个完整的优先级说明是十分复杂的，出于让您尽快入门的目的，先列出以下几点：

• 乘除法运算优先于加减法运算。因此2*3-1得到5，而不是4。2/3-1得到-1,而不是1(记住在整型除法中2/3结果是0)。
• 如果运算符有相同的优先级，它们会按照从左往右的顺序计算。因此表达式minute100/60中，乘法运算最先进行，得到5900/60，接下来进行除法运算，得到98.如果运算按照从右到左的顺序，结果会变成591，也即59，结果是错误的。
• 任何时候，如果你想要推翻优先级规则的限制(或者你不确定它们是什么)你可以使用圆括号。圆括号中的表达式会被优先计算，因此2*(3-1)结果是4.你同样可以使用圆括号来使表达式更易读，正如(minute*100)/60中所用的圆括号，尽管它并没有改变运算结果。

2.9 操作符

有趣的是，在整数上使用的数学运算同样可以被用在字符上，例如

char letter;
letter = 'a' + 1;
cout << letter << endl;

输出字母b。尽管对字符使用乘法在语法上是合法的，但这几乎从来都不会用到。

前面我说过你只能给整型变量赋整数值，给字符变量赋字符值，但这并不完全正确。在某些情况下，C++对类型进行了自动转换，例如，以下写法是合法的：

int number;
number = 'a';
cout << number << endl;

结果是97,C++中使用这一数字表示字母’a’。然而，把字符当做字符处理，把数字当做数字处理通常是一个好主意，除非有一个很好的理由，才把一种类型转换成另一种类型。

自动类型转换是在设计一种编程语言时存在的共同问题的一个例子，它和形式体系有冲突，形式体系要求形式语言，应该具备无例外的简单规则，然而便利性要求编程语言易用于实践。

大部分时候，便利性会胜出，这对于高手程序员通常是好事，他们摆脱了严格而笨拙的形式体系。但对于菜鸟程序员来说并非好事，复杂的规则以及大量的例外会使他们陷入困惑。在这本书中，我试图通过强调规则并忽略大多例外来简化学习。

2.10 组合

目前为止我们孤立地关注了程序设计语言中的一些元素—变量、表达式和语句，还没有谈到如何把它们组合起来。

程序设计语言中的一个最有用的特性是它们能使用小的构件，并把它们组合起来。例如，我们知道怎样做整数乘法，也知道怎样输出值，因而我们能同时做这两件事情：

cout << 17 * 3；

事实上，我不应该说“同时”，因为实际上乘法运算必须在输出之前，但是关键在于任何包含数字、字符和变量的表达式都可以用在输出语句中。我们已经见过这样的例子：

cout << hour*60 + minute << endl;

你同样可以将任意表达式放在赋值语句的右边：

int percentage;
percentage = (minute * 100) / 60;

这种能力现在看上去并不能让人印象深刻，但是接下来我们会看到另外一些例子，在那些例子中，组合整齐而简洁地表达出了复杂的计算。

警告：对于在何处使用特定的表达式有一些限制；尤其是赋值语句的左边必须是一个变量名，而不能是一个表达式。这是因为左侧表示结果的存储位置。表达式仅仅代表值，并没有代表存储位置，因此以下表达式是非法的： minute + 1 = hour;

2.11 术语表

变量（variable）：一个有名字的存储位置。所有的变量都有一个类型，决定了它能存储的值。

值（value）：一个字母或数字或其它可以被存储在变量中的东西。

类型（type）：一组值。目前我们见到的类型有整型(C++中用int表示)，字符型（C++中用char表示）

关键词（keyword）：编译器使用的保留字，用于解析程序。我们见过的例子包括int,void 和endl。

语句（statement）：代表一个命令或者动作的代码行，目前为止，我们见过的语句包括声明、赋值和输出语句。

声明（declaration）：创建变量并定义其类型的语句。

赋值（assignment）：为变量指定值的语句。

表达式（expression）：变量、表达式和值的组合。表达式同样具备类型，其类型由操作符和操作数决定。

操作符（operator）：代表简单计算（如加法或乘法）的特殊符号。

操作数（operand）：操作符操作的其中一个值。

优先级（precedence）：操作执行的顺序。

组合（composition）：将简单的表达式和语句组合成复合语句和表达式，以简明地表示复杂的计算 。

第3章 函数

3.1 浮点数

上一章我们曾遇到处理非整型数的问题。我们使用百分数代替小数，避开了这个问题。然而还有一种更通用的解决方案，即使用浮点数，可以同时表示小数和整数。C++有两种浮点类型：float和double，本书仅使用double型。

你可以创建浮点型变量并赋值，语法与使用其它数据类型一样。例如：

double pi;
pi = 3.14159;

声明变量同时赋值也是合法的：

int x = 1;
string empty = "";
double pi = 3.14159;

实际上这种语法形式很常用。声明和赋值的组合语法有时也称为初始化。 浮点数固然很有用，但也会带来混淆，因为整型数和浮点数之间可能有意义重叠。例如，1这个值，是一个整型数，还是一个浮点数，抑或二者都是？ 严格来说，C++区分整型的1和浮点型的1.0。尽管二者看似同一个数，但属于不同类型，严格意义上不允许类型间的赋值。下面语句是非法的：

int x = 1.1;

因为赋值运算符左边是整型变量，而右边是浮点型值。但是由于C++具有自动转换数据类型的特性，让你很容易就忘掉了这一规则。例如：

double y = 1;

严格来讲这也是非法的，但C++允许这么做，它会自动把int类型转换为double类型。这种放宽的限制带来便利的同时，也带来了问题，如：

double y = 1 / 3;

你可能以为此表达式给变量y的值会是一个合法浮点数0.333333，但实际上y的值却是0.0。原因是：赋值运算符右边的表达式实际上是两个整型值之比，所以C++做的是整型除法，使得此值为0；再转换为浮点数，结果就是0.0。 解决这个问题（当你发现问题是什么时）的一个方法是把右边变成一个浮点数表达式：

double y = 1.0 / 3.0;

此式给y赋的值是0.333333，这才是期望结果。 到目前为止我们接触到的所有运算操作——加、减、乘、除——对浮点数都有效，然而其背后的运行机制是完全不同的，你也许有兴趣想了解这一点。实际上，大多数处理器有特定的硬件来执行浮点数运算。

3.2 double到int的转换

前面讲到，C++可以在必要的时候自动将int转换为double，因为这种转换没有损失信息。反之，double转换为int则需圆整。C++不会自动执行这种转换，这是为了让程序员意识到，这样做会损失小数部分。

将浮点数转换为整型数的最简单方法是用类型转换(typecast)。之所以称之为类型转换，是因为它允许你将某种类型的一个值“回炉”成另一类型，这里“回炉”指的是再造或重塑，而非报废。

类型转换的语法形式与函数调用相似。例如：

double pi = 3.14159;
int x = int(pi);

int函数返回整型值，所以x的值是3。转换到整型往往要向下圆整，即使小数部分是0.99999999也要舍去。

C++的每个数据类型都有一个对应的函数，负责将其参数转换为相应的类型。

3.3 数学函数

在数学领域，你可能会看到sin和log这样的函数，也学过对sin(π/2)和log(1/x)这样的表达式求值。首先，要求出括号中表达式的值，这个值称为函数的参数。比如π/2约为1.571，若x为10则1/x的值为0.1。

然后你就可以通过查表或执行各种计算来求函数本身的值了。1.571的正弦是1，0.1的对数是-1（假设log函数是求以10为底的对数）。

对于求类似log(1/sin(π/2))这样的更复杂表达式的值，上述求解过程可反复进行。首先我们求出最里面那个函数的参数，然后求整个函数，如此反复。

C++提供了一组内置函数，包含了大多数你能想到的数学运算。调用这些数学函数的语法形式与其本身的数学符号很相似：

double log = log(17.0);
double angle = 1.5;
double height = sin(angle);

第一例中的log定义为求17的自然对数(底数为e)。还有一个函数名为log10，取以10为底的对数。

第二例求解的是变量angle的正弦值。C++设定赋给sin以及其他三角函数的参数都是以弧度为单位的。角度转弧度，需要先除以360，再乘以2π。

如果你不知道π精确到15位小数是多少，你可以使用acos函数计算出来。-1的arccos（反余弦）值就是π，因为π的余弦值是-1。

double pi = acos(-1.0);
double degrees = 90;
double angle = degrees * 2 * pi / 360.0;

在使用数学函数之前，需要包含math头文件。头文件包含了编译器需要知道的，却在你的程序之外定义的函数信息。比如"Hello, world!"这个例子中，我们通过使用include语句包含了名为iostream.h的头文件：

#include 

iostream.h包含了输入、输出（I/O）字节流的信息，包括一个名为cout的对象。

类似的，math头文件包含了数学函数的相关信息，可以在你的程序开头把它同iostream.h一起包含进去：

#include 

3.4 函数组合

C++函数就像数学函数一样可以组合，即你可以用一个表达式作为另一表达式的一部分。例如，你可以使用任意表达式作为函数的一个参数：

double x = cos(angle + pi/2);

这个语句把pi值除以2，再加到angle上，求得的值作为参数传给cos函数。

你也可以将一个函数的返回值作为参数传给另一个函数：

double x = exp(log(10.0));

这个语句求出以e为底的10的对数，再将此结果作为指数求e的幂，结果赋给x。但愿你明白是怎么回事。

3.5 添加新函数

到目前为止我们只使用了C++内置的函数，然而也可以添加新函数。实际上我们已经见过一个函数定义了：main。main这个函数名很特殊，因为它表示程序开始执行的地方，但main函数的语法形式和其它函数定义一样：

void 函数名(参数列表) {
  语句
}

你可以为自己的函数任意定义名称，但不能命名为main或者其它C++关键字。参数列表指定了使用（或称为调用）新函数所需要提供的信息（如果有的话）。

main函数定义中的空括号表示它不携带任何参数。我们首先要写的几个函数也是没有参数的，语法形式如下：

void newLine() {
  cout << endl;
}

此函数名为newLine，只有一个语句，用以输出换行符，其中换行用特殊值endl表示。

在main函数中，我们可以像调用C++内置函数一样调用这个新函数：

void main () { cout << "First Line." << endl; newLine (); cout << "Second Line." << endl; }

这段程序输出如下：

First line.

Second line.

注意：输出的两行之间有多余的空行。我们要想在两行之间出现更多的空行该怎么做呢？可以重复调用同一个函数：

void main ()
{
    cout << "First Line." << endl;
    newLine ();
    newLine ();
    newLine ();
    cout << "Second Line." << endl;
}

或者我们写一个新函数，命名为threeLine，作用是打印3个空行：

void threeLine ()
{
　　newLine (); newLine (); newLine ();
}
void main ()
{
    cout << "First Line." << endl;
    threeLine ();
    cout << "Second Line." << endl;
}

对于这个程序，你应该注意以下几点：

你可以反复调用同一处理过程，事实上这种做法是非常普遍、实用的。

你可以让一个函数调用另一函数。在本例中，main函数调用threeLine，threeLine又调用newLine。同样，这也是普遍、实用的做法。

在threeLine这个函数中，我一行写了三条语句，这符合语法规范（记住，空格和空行通常不改变程序的意义）。然而更好的方式通常是每条语句独占一行，这样程序更易读，我是为了节约篇幅才破坏了这条规则。

为什么我们值得费力气来创建这些新函数？到现在为止可能讲的还不是很清楚。实际上原因有很多，本例只说明了两点：

创建新函数使你有机会给一组语句起个名字。函数将一个复杂的计算过程隐藏在一个简单指令背后，并使用英语单词取代晦涩代码，可以起到简化程序的作用。试问，newLine和cout << endl，哪个更清晰呢？

创建新函数能够去除重复代码，使程序更短小。例如，连续打印九个空行的一种简单做法是调用treeLine三次，那么连续打印27个空行你要怎么做呢？

3.6 定义与使用

将前面章节所有的代码片段集中到一起后，整个程序如下：

#include 
void newLine ()
{
　　cout << endl;
}
void threeLine ()
{
　　newLine (); newLine (); newLine ();
}
void main ()
{
    cout << "First Line." << endl;
    threeLine ();
    cout << "Second Line." << endl;
}

这段程序包含3个函数定义：newLine、threeLine和main。

main函数内有一条语句使用（调用）了threeLine。同样的，threeLine调用了三次newLine。请注意，每个函数定义都出现在调用之前。

在C++中这是必需的：函数的定义必须出现在第一次使用之前（之上）。你可以把函数顺序调换一下，然后尝试编译程序，看得到什么错误信息。

3.7 多函数编程

当你看一个包含若干函数的类定义时，习惯从头看到尾，但这有可能带来混淆，因为这并不是程序的执行顺序。

程序往往从main函数的第一条语句开始执行，不管它出现在程序的什么位置（通常在最底部）。语句被逐条执行，直到遇到函数调用处。函数调用就像程序执行流程中的回转道，使你来到被调函数的第一行代码——而非顺序上的下一条语句，然后执行所有的函数语句，再回到刚才中断的地方，继续下去。

听起来简单的可以，但你得记住一个函数可以调用另一个函数。这样，我们在执行main函数中途会停住，然后去执行threeLine的语句；而在执行threeLine时，有可能中断3次转而去执行newLine。

所幸的是C++擅长这种追踪足迹的工作，所以每当newLine执行完时，程序总能重拾在threeLine中的中断之处，最终回到main，因而程序总有终止的时候。

这个麻烦的故事告诉我们什么呢？当你读程序的时候，不要从头读到尾，而要跟着执行流程走。

3.8 参数与参数值

我们用过的一些内置函数携带参数，即你提供给函数让它工作的一些值。比如，如果你想计算一个数的正弦值，你需要指定这个数是多少。因此sin函数使用一个double值作为参数。

一些函数携带一个以上的参数，如pow携带两个double参数，分别作为底数和幂。

注意，在所有这些例子中，我们不仅要指定参数的个数，还要指定参数的类型。所以当你写一个类定义时，发现参数列表指定了每个参数的类型，这应该没什么奇怪的。例：

void printTwice (char phil) {
   cout << phil << phil << endl;
}

此函数携带一个参数，名称为phil，类型为char。不管这个参数是什么（光看这些我们也不知道它是什么），它都要被打印两次，然后是一个空行。我选择给这个参数命名为phil，只是想说明你的参数名称由你决定，但是一般情况下你要选择一个比phil更直白的名字。

调用这个函数需要我们给一个char值。例如，我们可以定义main函数如下：
void main () {
  printTwice (’a’);
}

你提供的这个char值被称作参数值，我们称参数值被传递给函数。这种情况’a’作为参数值传给了printTwice，它将被打印两次。

换一种方式，如果我们定义了一个char变量，就可以换用此变量做参数值：

void main () {
     char argument = ’b’;
     printTwice (argument);
}

注意这里一点非常重要：作为参数值传给函数的变量名（argument）跟函数的参数名（phil）没有任何关系。我再重申一遍：

作为参数值传给函数的变量名跟函数的参数名没有任何关系。

它们可以同名也可以不同名，但重要的是你必须认识到它们不是同一个东西，除非它们碰巧值相同（本例中它们都是字符’b’）。

传给函数的参数值必须和函数的参数具有相同的类型。这是条重要的规则，但有时会混淆，因为C++会自动转换参数值的类型。现在你应该了解这些普遍规则，后面我们再讨论例外情况。

3.9 参数和变量的局部性

参数和变量只存在于它们所在的函数内部。在main函数内部，没有phil这个东西存在。如果你想使用这个变量，编译器会报错。同样的，在printTwice内部，也没有argument这个变量。

类似这样的变量被称为局部变量。为了跟踪参数和局部变量，画一张栈图还是很有用的。像状态图一样，栈图展示出每个变量的值，然而变量都包含在大方框里，大方框表示变量所属的函数。

例如，printTwice的栈图如下：

每当函数被调用，就会创建此函数的一个实例。函数的每个实例都包含自己的参数和局部变量。上图中外面带函数名的方框代表函数实例，方框里面是函数的参数和局部变量。

此例中，main函数有一个局部变量argument，没有参数。printTwice没有局部变量，有一个参数phil。

3.10 多参函数

声明和调用多参函数的语法往往成为错误的诱因。首先，要记住必须声明每个参数的类型。例：

void printTime (int hour, int minute) {
    cout << hour;
    cout << ":";
    cout << minute;
}

很容易写成(int hour, minute)，这种形式用于变量声明是合法的，但用于参数声明就不行。

另一个容易混淆的地方是，你不需要声明参数值的类型。下面这段代码是错误的！

int hour = 11;
int minute = 59;
printTime (int hour, int minute);     // 错误！

本例中，编译器看到声明语句就可以知道hour和minute的类型。传递参数值时给出类型是不必要的，也是非法的。正确的语法形式是printTime(hour, minute)。

3.11 有返回值的函数

你也许注意到了，到现在为止我们使用的一些函数都会给出执行结果，如数学函数；另外一些函数只执行，并不返回任何值，如newLine。于是问题来了：

如果你调用一个函数但并没有用到其返回值，会发生什么（例如，你并不会把这个返回值赋给某个变量，或者把它作为一个更大的表达式的一部分）？

如果你用一个无返回值的函数作为表达式的一部分，如newLine() + 7，会发生什么？

我们可以编写有返回值的函数吗？还是说我们只能写newLine和printTwice这样的函数呢？

第三个问题的答案是：是的，你可以编写带返回值的函数，本书很多章节都是这么做的。另外两个问题留给你，试验一下再回答。无论何时遇到类似在C++里是不是合法这样的问题，一个好办法是让编译器回答你。

3.12 术语表

浮点数（floating-point）：一种变量或值的类型，包含整数和小数。C++有几种浮点类型，本书使用的是double。

初始化（initialization）：用于声明新变量并赋值的语句。

函数（function）：命名的一组语句序列，执行某种功能。函数可带参数，也可不带，可返回结果，也可不返回。

参数（parameter）：调用函数时提供给函数的信息。参数与变量很类似，它们含有值和类型。

参数值（argument）：调用函数时提供给函数的值。参数值的类型必须与对应的参数类型相同。

调用（call）：执行函数。

第4章 条件和递归

4.1 取模操作符

取模操作符用于对整数（以及整数表达式）进行操作，得到第一个操作数除以第二个操作数的余数。在C++中，取模操作符用一个百分号%表示。它的语法和其他操作符完全相同：

int quotient = 7 / 3;
int remainder = 7 % 3;

第一个操作符是整数除法，得到结果2。第二个操作符得到结果1。因此，7除以3得2余1。

取模操作符是非常有用的。例如，你可以用它检验一个数能否可以被另一个数整除:如果x % y得到0，说明x可以被y整除。

同样，你可以使用取模操作符提取一个数的最右边的一位或多位数字。例如，x % 10得到x（十进制数）最右侧那位数字。类似地，x % 100得到最后两位数字。

4.2 条件执行

为了写出更实用的程序，我们几乎总是需要检查特定条件，并相应地改变程序的行为。条件语句给了我们这种能力。最简单的形式是if语句：

if( x > 0){
 cout << "x is positive" <<endl;
}

圆括号中的表达式被称为条件。如果条件为真，则花括号中的语句会被执行。否则不执行。

条件可以包括任何比较操作符：

x == y               //x等于y
x != y               //x不等于y
x > y                //x大于y
x < y                //x小于y
x >= y               //x大于或等于y
x <= y               //x小于或等于y

尽管你可能很熟悉这些操作符，但C++使用的语法和数学符号有一些不同，如=，≠和≤。一种常见的错误是使用单个=来代替两个==。记住“=”是赋值操作符，而==是比较操作符。此外，C++中不存在类似=这样的操作符。

条件操作符两侧必须是相同的类型。你只能把int类型和int类型比较，把double类型和double类型比较。很遗憾，此时，你根本不能比较字符串！存在一种比较字符串的方法，但在最近几章内我们都不会学到它。

4.3 选择执行

第二种形式的条件执行是选择执行，选择执行中存在有两种可能，由条件表达式来决定哪种可能被执行。语法看起来像这样：

if( x%2 == 0) {
  cout << "x is even" << endl;
}else{
  cout << "x is odd" << endl;
}

如果x除以2得到的余数是0，则我们知道X是偶数，代码会输出一条信息表明此意。由于条件非真即假，因而有且仅有一条语句会被执行。

说句题外话，如果你认为你经常需要检验数字的奇偶性（偶数性或奇数性），你可能想把这段代码“包装”到一个函数里：

void printParity (int x) {
  if (x%2 == 0) {
     cout << "x is even" << endl;
  } else {
     cout << "x is odd" << endl;
  }
}

现在你有了一个名为printParity的函数，它会为任何你愿意提供的整数输出合适的信息。在main方法中，你可以这样调用它：

printParity (17);

要永远记住当你调用一个函数时，不需要声明你提供的参数的类型。C++可以知道它们是什么类型。你应该抵制诱惑，别把代码写成这样：

int number = 17;
printParity (int number)；         // 错误!!!

4.4 链式条件

有时候你希望检查多个相关的条件，然后从多个操作中选择一个。其中一种方法是链接多个if和else：

if(x > 0) {
   cout << "x is positive" << endl;
} else if (x < 0) {
   cout << "x is negative" << endl;
} else {
   cout << "x is zero" << endl;
}

这些链条可以有任意长，然而如果它们失控，将会难以阅读。为了让它们变得更易读，一种方法是使用标准缩进，正如这些示例中证明的。如果你把所有这些语句和花括号都整齐地排列起来，那么你犯语法错误的可能性会减小，就算犯错了，也能更快地找出它们。

4.5 嵌套条件

除了链接外，你还可以把一个条件嵌套到另一个条件中。之前那个例子我们可以写成这样：

if (x == 0 ) {
  cout << "x is zero" << endl;
} else {
   if (x > 0){
     cout << "x is positive" << endl;
   } else {
     cout << "x is negative" << endl;
   }
}

现在有一个外层条件，包含着两条分支。第一条分支包含了一个简单的输出语句，但第二条分支包含着另一个if语句，这个if语句本身有两条分支。幸运的是，这两条分支都是输出语句，可它们同样可以是条件语句。

再次注意到缩进的使用使得代码结构更加清晰，然而嵌套语句很难快速地阅读。通常，一个好方法是尽量避免使用嵌套语句。

另一方面，这类嵌套结构很常见，我们还会再次和它碰面，因此你最好习惯它。

4.6 return语句

return语句允许你在一个函数执行到结尾之前终止它的执行。使用它的一个理由是如果你检测到一个错误的条件：

#include 

void printLogarithm (double x) {
   if (x<=0.0) {
      cout << "Positive numbers only,please." << endl;
      return;
   }

   double result = log(x);
   cout << "The log of x is " << result;
}

程序中定义了一个printLogarithm函数，它把一个double类型的变量x作为参数。此函数一开始会检查x是否小于或等于0，如果是，则会输出一条错误信息并使用return语句退出函数。执行流程会立刻回到调用方，函数的剩余部分不会被执行。

我在条件的右侧使用了一个浮点值，这是因为左边是一个浮点型变量。

任何时候都需要记住，如果你需要使用一个math库里的函数，你必须包含头文件math.h。

4.7 递归

上章中我提到一个函数调用另一个函数是符合语法的，而且我们已经见过好几个例子。但我还没有告诉你们，一个函数调用它自己也是合法的。这是件好事，理由可能不那么显而易见，但事实证明它是一个程序能做的最具魔力也最有趣的事情之一。

例如，下面这个函数：

void countdown( int n) {
  if (n == 0) {
    cout << "Blastoff! << endl;
  } else {
    cout << n << endl;
    countdown (n-1);
  }
}

函数名是countdown，它把单个整数作为参数，如果参数是0，则输出单词“Blastoff”。否则输出这个参数，然后调用countdown函数–也即它自身–传入n-1作为输入参数。

如果我们这么调用这函数，会发生什么呢？

void main ()
{
  countdown (3);
}

countdown从n=3开始执行，由于n不为0，所以它输出值3，然后调用它自己…

countdown从n=2开始执行，由于n不为0，所以它输出值2，然后调用它自己…

countdown从n=1开始执行，由于n不为0，所以它输出值2，然后调用它自己…

countdown从n=0开始执行，由于n为0，所以它输出单词“Blastoff!”，然后返回。

countdown得到返回值n=1。

countdown得到返回值n=2。

countdown得到返回值n=3。

然后你会回到main函数（多美妙的一次旅行！）。因此输出看起来会是这样：

3
2
1
“Blastoff!”

作为第二个例子，让我们再来看看函数newLine和threeLine。

void newLine() [
  cout << endl;
}

void threeLine() {
   newLine();   new Line();   new Line();
}

尽管它们奏效，但如果我希望再输出2个或者106个换行符，它们并不能帮我们太多。一种更好的替代方法是这样：

void nLines(int n){
  if (n > 0) {
     cout << endl;
     nLines (n-1);
  }
}

这段程序和countdown很相似，只要n大于0，它就会输出一个换行符，然后调用它自身来输出另外的n-1行。因此，总的换行符个数是1+(n-1), 最后得到n

一个函数调用它自身的过程被称为递归，这些函数被称为递归的。

4.8 无穷递归

在前面几节的例子中，可以发现每次函数被递归调用，参数会递减1，因此最终变为0。此时函数会立刻返回，不再做递归调用。这种情况–当函数结束而不再做递归调用–被称为基础情况。

如果一个递归永远不能到达基础情况，它会一直递归调用下去，程序永远不会终止。这称为无穷递归，这通常并不是一个好主意。

在大多数编程环境中，一个有着无穷递归的程序并不会真的永远运行下去。最终会出现中断，程序报告一个错误。这是目前我们看到的第一个运行时错误（直到运行程序才会出现的错误）的例子。

你应该写一个无穷递归的小程序，运行起来看看会发生什么。

4.9 递归函数的栈图

在前面的章节中，我们使用了一个栈图来表示一个程序在函数调用时所处的状态。 同样的图形也能使得递归函数的解释变得更容易些。

每次函数被调用，它都会创建一个新的实例，包含着函数的局部变量和参数。

本图说明了函数countdown的一个栈图,调用时n的初始值为3；

图中有一个main函数的实例和四个countdown函数的实例，每个实例中的参数n的值都不同。栈底的countdown实例n取值为0。它没有进行递归调用，因此没有更多的countdown实例。

main函数的实例是空的，因为main函数没有任何参数或者局部变量。作为一个练习，请你为nLines画出一个栈图，参数n取值为4。

4.10 术语表

模（modulus）：一种用于整数的操作符，当一个数被另一个数除时得到余数。C++中用百分号(%)来表示。

条件句（conditional）：一个语句块，由一些条件来决定是否执行。

链（chaining）：一种依次连接多个条件语句的方式。

嵌套（nesting）：把一个条件语句放在另一个条件语句的一个或两个分支中。

递归（recursion）：调用你当前正在执行的同一函数的过程。

无穷递归（infinite recursion）：一个函数递归调用它自身，永远不能到达基础情况。最终无穷递归会导致运行时错误。

第5章 有返回值的函数

5.1 返回值

前面我们用过的一些内置函数（如数学函数）都会生成结果值。也就是说，调用函数的效果是产生一个新值，一般我们会把这个值赋给变量，或用作表达式的一部分。例如：

double e = exp(1.0);
double height = radius * sin(angle);

但到目前为止，我们编写的所有函数都是void函数，它们不返回任何值。调用void函数时，常见的是函数调用语句本身占一行，没有赋值操作：

nLines(3);
countdown(n-1);

本章我们将学习编写带有返回值的函数，因为没有更好的名字，我索性直接称之为“有返回值的函数”。第一个例子是area函数，它以一个double值为参数，返回以给定参数值为半径的圆的面积：

double area(double radius) {
  double pi = acos(-1.0);
  double area = pi * radius * radius;
  return area;
}

首先要注意到，该函数定义的开始部分与void函数（如果以“void”开始，则说明这是void函数）不同，这里使用了double，说明函数返回double类型的值。

再就是注意最后一行，这是return语句的一种可选形式，它带了一个返回值。这句话的意思是，”以其后的表达式为返回值，立即从函数返回。“表达式可以非常复杂，所以area函数可以简化为：

double area(double radius) {
  return acos(-1.0) * radius * radius;
}

另一方面，像area这样的临时变量会使调试更容易。不管哪种情况，return语句中表达式的类型必须与函数的返回类型匹配。换句话说，当把函数的返回类型声明为double时，就要保证函数最终会得到一个double值。如果不返回任何表达式，或者返回了类型不匹配的表达式，编译器都会报错。

有时包含多个返回语句是有用的，比如每个分支一个：

double absoluteValue(double x){
  if (x < 0) {
    return -x;
  } else {
    return x;
  }
}

这些return语句分布在不同的条件分支中，只有一个能执行。虽然函数可以有多个return语句，但是只要其中一个执行，函数也就随之结束了，不会再执行后面的语句。

return语句后面的代码，或任何不可能执行到的代码，称为“死代码”。如果存在死代码，有的编译器会给出警告。

如果return语句在一个条件分支中，必须保证每个可能的路径都能碰到return语句。例如：

double absoluteValue(double x) {
  if(x < 0) {
    return –x;
  } else if(x > 0) {
    return x;
  }            // 错误
}

这个函数是错误的，因为当x为0的时候，所有条件都不满足，最终函数找不到相应的return语句。非常不幸，很多C++编译器并不捕捉此类错误，程序可以通过编译并运行，但是当x==0时返回值可能是任意值，而且在不同环境下也可能有不同表现。

现在你可能还是很讨厌看到编译错误信息，但是随着经验的增长，你会意识到：当程序有错误时，不出现编译错误会比出现更糟糕。

有时会有这样的事情，你用一些值测试了absoluteValue函数，而且该函数看起来是可以正常工作的，可是当你把程序交给别人在其他环境下测试时，却出现了不可思议的bug，经过几天的调试你才发现absoluteValue的实现有问题。要是编译器能早发现问题并警告你该多好啊！

从现在开始，如果编译器指出了程序中的错误，请不要抱怨编译器。相反，你应该感谢编译器帮你找出错误，而且节约了你数天的调试时间。有的编译器可以通过选项指定更严格的编译检查并报告所有错误。你要一直开着这些选项。

说句题外话，math库中的fabs函数能够正确计算double变量的绝对值。

5.2 程序开发

现在你应该可以阅读并理解一个完整的C++函数了。但是到底怎么设计函数可能还不清楚。我会马上介绍增量开发技术。

举个例子，假设要计算两点之间的距离，其中两个点分别用坐标 (x1, y1)和(x2, y2)表示。按照定义，

第一步要考虑的是，在C++中距离函数应该如何表示，也就是要确定函数的输入（即参数）和输出（即返回值）。

在这个例子中，两个点就是参数，很自然，可以用四个double值表示。返回值就是距离，也是double类型的。

我们已经可以写出这个函数的轮廓了：

double distance (double x1, double y1, double x2, double y2) {
  return 0.0;
}

返回语句只是用于占位，以便函数通过编译并返回一个值，即使这个值是不正确的。眼下这个函数并没有做什么有用的事情，但尝试编译一下这个函数还是值得的，因为这样可以在函数变得更复杂之前发现任何语法错误。

为了测试这个新函数，我们必须使用样本值值调用它。在main函数的某个位置我添加了下面语句：

double dist = distance (1.0, 2.0, 4.0, 6.0);
cout << dist << endl;

我选择这些值，这样两个点的水平距离是3，垂直距离是4；那样，距离就是5（3-4-5直角三角形的斜边）。测试函数时，知道正确答案是有用的。

一旦函数定义的语法验证无误，我们就可以开始一次一行的添加代码了。每次增量改变，我们都重新编译并运行程序。这样，在任何点我们都能精确地知道错误的位置——肯定是在我们最后增加的代码中。

计算的下一步就是求出x2−x1和y2−y1的差。我会把这些值存在临时变量dx和dy中。

double distance (double x1, double y1, double x2, double y2) {
  double dx = x2 - x1;
  double dy = y2 - y1;
  cout << "dx is " << dx << endl;
  cout << "dy is " << dy << endl;
  return 0.0;
}

我添加了输出语句，在继续之前先验证中间值。前面提到过，我们已经知道这两个值应该是3.0和4.0。

函数完成之后我会删除输出语句。这样的代码称为支架代码，因为它虽然有助于构建程序，但并非最终产品的组成部分。有时保留支架代码，仅将其注释掉是个好想法，以防后面再用到。

开发的下一步就是求dx和dy的平方。我们可以使用pow函数，但更简单快捷的方法是通过每一项自乘来计算。

double distance (double x1, double y1, double x2, double y2) {
  double dx = x2 - x1;
  double dy = y2 - y1;
  double dsquared = dx*dx + dy*dy;
  cout << "dsquared is " << dsquared;
  return 0.0;
}

现在，再次编译运行程序，并检查中间值（它应该是25.0）。

最后，可以使用sqrt函数计算并返回结果。

double distance (double x1, double y1, double x2, double y2) {
  double dx = x2 - x1;
  double dy = y2 - y1;
  double dsquared = dx*dx + dy*dy;
  double result = sqrt (dsquared);
  return result;
}

然后，我们应该在main函数中输出并验证结果值。

随着编程经验的增多，你会发现自己可以一次编写和调试多条语句。不过，增量开发过程能节省很多调试时间。

这一过程的几个关键方面是：

• 从一个小的、可以工作的程序开始，加以微小的增量变化。在任何时候，如果出现错误，都能精确地知道错误位置。

• 使用临时变量保存中间值，以便于输出并验证它们。

• 一旦程序正常工作，你可能想删除一些支架代码或者将多条语句合并为符合表达式，但要确认这不会让代码难以阅读。

5.3 组合

正如你所期待的那样，一旦定义了一个新函数，你既可以将它用作表达式的一部分，也可以用现有的函数构造新的函数。举个例子，给定圆心和圆周上的一点，如何计算圆的面积？

假设圆心坐标保存在变量xc和yc中，而圆周上那点的坐标是xp和yp。第一步就是计算圆的半径，也就是这两点间的距离。幸运的是，我们前面定义的distance函数就是计算两点间距离的。

double radius = distance(xc,yc,xp,yp);

第二步就是使用半径计算圆面积并返回。

   double result = area(radius);
   return result;

然后将这两步封装在一个函数中：

double fred(double xc,double yc,double xp,double yp){
  double radius = distance(xc,yc,xp,yp);
  double result = area(radius);
  return result;
}

函数名fred可能看起来很奇怪。我下一节再解释原因。

临时变量radius和area对开发和调试而言是有意义的，程序工作正常之后我们就可以通过组合函数调用使代码更简洁：

double fred(double xc,double yc,double xp,double yp){
  return area(distance(xc,yc,xp,yp));
}

5.4 重载

前面几节你可能已经注意到，fred和area两个函数功能类似，都是计算圆的面积，但参数不同。area函数需要提供半径，而fred函数需要两点的坐标。

如果两个函数做同样的事情，给它们起相同的名字是很自然的。换句话说，fred也叫做area会更有意义。

重载是指存在多个同名函数，只要每个函数接受的参数不同，在C++中就是合法的。所以我们可以再进一步，重命名fred函数：

double area (double xc, double yc, double xp, double yp) {
  return area (distance (xc, yc, xp, yp));
}

看起来这像个递归函数，其实不然，实际上这一版本的area函数在调用另一个版本的area函数。调用重载函数时，C++可以通过调用者提供的参数来来确定要调用的版本。比如：

double x = area (3.0);

C++会寻找名为area且以一个double值为参数的函数，所以这里使用的是area的第一个版本。而对于下面语句：

double x = area (1.0, 2.0, 4.0, 6.0);

C++会使用area的第二个版本。

很多内置的C++命令都是已经重载的，也就是说有不同的版本用以接受不同数目或不同类型的参数。

虽然重载是很有用的特性，但使用时一定要小心。使用不当可能让自己都迷惑了，比如你想调试重载函数的一个版本，却意外地调用了另一个版本。

实际上，这提醒了我调试的一个基本规则：**一定要确认你正在看的程序版本和就是正在运行的版本！**有时你可能会发现你一点点的修改程序，可是每次程序运行后输出都是一样的。这是一个警告信号，因为运行的程序版本并不是你想象的那个。为了证明无误，每次修改代码时，贴上一行输出语句（输出什么并不重要），以此确认程序的行为确实相应地改变了。

5.5 布尔值

到目前为止我们看到的类型都能表示很大范围的数据，整数多的是，而浮点数更多。相对而言，字符集的规模小的多。C++中还有一个类型表示的范围更小，即布尔类型，它只能表示true和false两个值。

虽然没提到过该类型，但我们前面几章中实际已经使用过布尔值了。if语句和while语句中的条件就是布尔表达式。比较操作符的结果也是布尔值。例如：

if (x == 5) {
  // 进行某些处理
}

==操作符比较两个整数，得到一个布尔值。

布尔值true和false是C++的关键字，可以在任何需要布尔表达式的地方使用。例如：

while (true) {
  // 无限循环
}

这是无限循环（也可以在遇到return或break语句的时候结束）的一个标准惯用法。

5.6 布尔变量

照例，每个类型的值都有一个相应类型的变量。C++中的布尔类型叫做bool。布尔变量的使用和其他类型类似，如：

bool fred;
fred = true;
bool testResult = false;

第一行是一个简单的变量声明；第二行是个赋值；第三行是声明和赋值的组合，叫做初始化。

前面提到过，比较操作符的结果是布尔值，所以可以将结果保存在布尔变量中，如：

bool evenFlag = (n%2 == 0); // 当n为偶数时为true
bool positiveFlag = (x > 0);    // 当n为正数时为true

然后可以将布尔变量作为条件表达式的一部分使用：

if (evenFlag) {
  cout << "n was even when I checked it" << endl;
}

以这种方式使用的变量称为“标记”，因为它标记了一些条件存在与否。

5.7 逻辑操作符

C++中有三种逻辑操作符：与，或，取反，分别用符号**&&，||和！**表示。这些操作符的语义与它们的字面意思类似。例如 x > 0 && x < 10 为真，当且仅当x大于0且小于10的时候成立。

evenFlag || n%3 == 0，当两个条件中的任一个为真时，表达式为真，即evenFlag为真或n可以被3整除时。

取反操作符的作用是为布尔表达式求反， !evenFlag这个表达式当evenFlag为假时， 即数字为奇数时，表达式为真。

逻辑操作符的一个作用是简化嵌套的条件语句。例如，下面代码怎样用单个条件来表达？

if (x > 0) {
    if (x < 10) {
        cout << "x is a positive single digit." << endl;
    }
}

5.8 布尔函数

和返回其他任何类型一样，函数也能返回布尔值，将复杂的条件测试隐藏在函数中非常方便。例如：

bool isSingleDigit (int x)
{
  if (x >= 0 && x < 10) {
    return true;
  } else {
    return false;
  }
}

函数名是isSingleDigit。布尔函数常见的命名方式是，让名字听起来像是在提问题，回答是否即可。布尔函数的返回类型是bool，这意味着函数中的每个return语句都要提供一个布尔表达式。

例子中的代码比较直接，虽然实际可能不需要这么长。还记得表达式 x >= 0 && x < 10吧，它也是布尔类型，所以直接返回该表达式是没问题的，还可以避免if语句。

bool isSingleDigit (int x)
{
  return (x >= 0 && x < 10);
}

在main函数中，可以以常规的方式调用该函数：

cout << isSingleDigit (2) << endl;
bool bigFlag = !isSingleDigit (17);

第一行输出为真，因为2只有一位。不幸的是，C++输出布尔值的时候，并不直接显示“true”和“false”，而是显示整数1和0（可以通过boolalpha标记来修复这个问题，不过这个方式太过丑陋，我都不想提及）。

第二行中，只有当17是一位的数字时，bigFlag会被赋值为true。

最常见的用法是将布尔函数放在条件语句中：

if (isSingleDigit (x)) {
  cout << "x is little" << endl;
} else {
  cout << "x is big" << endl;
}

5.9 从main函数返回

现在我们已经学习了带返回值的函数，我来告诉你一个秘密：main函数并非真的应该是一个void函数。main应该返回一个整数：

int main ()
{
  return 0;
}

通常，main的返回值为0，它表明程序成功执行。出错时一般返回-1，或其他的用以指明发生了哪种错误的值。

当然，你可能想知道这个值返回给谁了，因为我们自己从来没有调用过main。其实是这样，当系统执行程序时，它通过调用main开始，这和main调用其他函数的方式一样。

系统甚至会给main传递一些参数，但我们暂时不准备处理它们。

5.10 深入递归

到目前为止，我们只学习了C++的一个子集，但是你可能有兴趣知道，这个子集可以算作一个完整的编程语言，任何可计算的事物都可以用该子集表达。任何现有的程序都能通过我们学过的这些仅有的语言特征来重写(实际上，我们还需要一些控制键盘、鼠标、硬盘等设备的命令，就这些了)。

证明这个论断并不是个简单的练习，最早由阿兰图灵完成，他是最早的计算机科学家之一(很多人可能争辩说他是数学家，但是很多早期的计算机科学家都是从数学家开始的)。相应地，这个结论也称为图灵理论。如果你选了计算理论课程的话，你有机会看到相关证明的。

5.11 思路跳跃

跟踪程序执行流程是阅读代码的一种方式。另一种可选的方式我称之为“思路跳跃”。 当你遇到一个函数调用，我们不去跟踪执行流程，而是假定函数工作正常并返回合适的值。

事实上，我们前面已经使用过思路跳跃，比如调用内置函数。当调用cos或exp时，我们并没有检查函数的实现。我们只是假定这些函数能正常工作，因为设计库的都是很厉害的程序员。

调用自己写的函数也是如此。例如，在5.8节我们写了一个函数isSingleDigit用来判断一个数是否处于0和9之间。只要能够通过测试或者检查代码确定这个函数是正确的，我们就能再次使用这个函数而不需要检查代码。

这个方法同样适用于递归函数。碰到递归调用时，我们不是跟踪执行流程，而应假定递归调用正常工作(能产生正确的结果)，然后提出问题，“假设能够计算n-1的阶乘，能否计算n的阶乘？”。很明显，可以通过n-1乘以n来计算n的阶乘。

当然，当你甚至还没有编写完的时候就假设函数正常工作可能有点奇怪，但是这也是我称之为“思路跳跃”的原因

5.12 又一个例子

前面的例子中，我使用了临时变量，这样便于把步骤讲清楚，代码也容易调试，但是我们也可以少写几行：

int factorial (int n) {
  if (n == 0) {
    return 1;
  } else {
    return n * factorial (n-1);
  }
}

从现在开始，我倾向于使用更简洁的版本，但我仍然建议你在开发过程中使用更清晰的版本。当代码正常工作后，如果你能感到鼓舞的话，可以收紧代码。

除了阶乘，另一个经典的例子是递归定义的数学函数fibonacci，它定义如下：

fibonacci(0) = 1
fibonacci(1) = 1
fibonacci(n) = fibonacci(n − 1) + fibonacci(n − 2);

翻译为C++，就是：

int fibonacci (int n) {
  if (n == 0 || n == 1) {
    return 1;
  } else {
    return fibonacci (n-1) + fibonacci (n-2);
  }
}

如果你想跟踪这个函数的执行流程，即使很小的n值，都会让你的头爆炸了。但是根据“思路跳跃”方法，假定两个递归调用工作正常(是的，可以做两次递归调用)，然后，很明显将它们加起来就是正确结果了。

5.13 术语表

返回类型(return type)：函数返回值的类型。

返回值(return value): 函数调用得到的结果值。

死代码(dead code): 代码中永远不会执行的部分，往往因为出现在return语句之后而无法执行。

支架代码(scaffolding)：在程序开发过程中使用但是不会出现在最终版本中的代码。

void：一个特殊的返回类型，用以说明void函数，既没有返回值的函数。

重载(overloading)：存在多个同名但参数不同的函数。调用重载函数时，C++可以根据提供的参数确定调用的版本。

布尔(boolean)：可以取两个状态之一(通常称为true和false)的值或变量。C++布尔值存储在bool类型的变量中。

标记(flag)： 一个记录条件或状态信息的变量(通常是布尔类型)。

比较操作符(comparison operator)：用来比较两个值的操作符，结果是一个表明两个操作数关系的布尔值。

逻辑操作符(logical operator)：用来组合布尔值以测试复合条件的操作符。

第6章 迭代

6.1 多次赋值

对同一变量多次赋值在C++里是合法的，这一点之前并没有多说。第二次赋值的效果是用新值替换掉旧值。

int fred = 5;
cout << fred;
fred = 7;
cout << fred;

这段代码输出57，因为第一次打印fred时，其值是5；第二次打印时其值为7。

这种多次赋值的机制正是我把变量形容为值的容器的原因。在为变量赋值时，修改的是容器里的内容，如图所示：

当存在对同一变量的多次赋值时，区分赋值语句和判等语句就显得尤为重要。C++使用=符号做赋值操作，因此很容易把诸如a=b这样的语句理解为判等语句。事实不是这样！

首先，相等是可交换的，而赋值不可以。比如，数学上若a=7则7=a，但是在C++里语句a=7;是合法的，7=a则不合法。

此外，数学上的等式永远为真。若现在a=b，则a永远等于b。在C++里，赋值语句可以使两个变量相等，但这两个变量未必总是相等的。

int a = 5;
int b = a; // 现在a和b相等
a = 3; // a和b不再相等

第三行改变了a的值，但未改变b的值，所以二者不再相等。在很多编程语言中，为避免混淆，赋值用另一种符号代替，如<-或:=。

尽管多次赋值非常有用，但尚需谨慎使用。如果变量的值在程序的不同部分总是在改变，代码就会非常难以阅读和调试。

6.2 迭代

重复性工作自动化是计算机常见用途之一。计算机善于重复执行相同或相似的任务而不出差错，人则不擅此道。

我们已经见到过使用递归执行重复工作的程序，如nLines和countdown。这种重复工作称为迭代。C++提供的几种语言特性使迭代程更序易编写。

我们将要学习的两种特性是while和for语句。

6.3 while语句

我们可以使用while语句重写countdown函数：

void countdown (int n) {
    while (n > 0) {
    cout << n << endl;
    n = n-1;
    }
    cout << "Blastoff!" << endl;
}

你几乎可以像阅读英语一样阅读while语句。这段代码的含义是：当n大于0时，继续显示n的值，然后将n减少1；当n变为0时，输出单词“Blastoff!”。

while语句执行流程的更正式的描述如下：

1. 对括号内的条件表达式求值，得到true或false；
2. 如果条件为false，退出while语句，继续执行下一条语句；
3. 如果条件为true，执行花括号里的没一条语句，然后回到第1步。

这类流程成为循环，因为第3步会回到起点。注意，如果初次进入循环判断条件为false，循环内的语句将不会执行。循环内的语句成为循环体。

循环体应改变一个或多个变量的值，使循环条件最终能变为false，以结束循环。反之，循环将永远反复执行，这种情形称为无限循环。本着娱乐无限的精神，计算机科学家发现下面这个洗发指导步骤是一个无限循环：抹洗发水，清洗，然后重复。

在countdown这个例子中，我们可以证明循环会结束，因为已知n的值是有限的，而且我们看到n在每次循环（迭代）后都会减小，所以最终n的值会变为0。另外一个例子就不好说了：

void sequence (int n) {
    while (n != 1) {
        cout << n << endl;
        if (n%2 == 0) { // n为偶数
            n = n / 2;
        } else { // n为奇数
            n = n*3 + 1;
        }
    }
}

循环条件是n!=1，因而循环将持续下去，知道n变为1，是条件为false。

每一次迭代，程序输出n的值，然后检查n是奇数还是偶数；如果是偶数，则n的值要除以2；如果是奇数，则n的值用3n+1取代。举个例子，如果循环初值（作为参数传给sequence）为3，结果序列就是3、10、5、16、8、4、2、1。

由于n或增或减，并没有明显证据能证明n一定会变到1，或者说程序会结束。对于n的某些特定值，我们可以证明程序会结束。例如，如果初值是2的幂，则n的值每次循环结果都是偶数，最终会变到1。前面的例子，初值是16，程序就在输出一个序列后结束。

不考虑特定值，我们是否能证明程序对于n的所有值都能结束？这个问题很有趣。到目前为止，没有人能够证明之，但也没有人能推翻之！

6.4 制表

生成表格式数据是能够从循环机制受益的事情之一。举个例子，在计算机成为常用设备之前，人们必须手工计算对数、正余弦以及其他常用的数学函数。为使这类工作更简单，产生了一些书，包含了一些长表格，你可以查出不同函数的值。创建这些表的工作是缓慢而繁琐的，而且结果容易大量出错。

当计算机登上了历史舞台，人们最初的反应是：“太棒了！我们可以用计算机准确无误的生成这些表。”这是个（大部分）正确但短视的看法。没多久，计算机和计算器普及，数学表就过时了。

好吧，应该说基本上过时了。事实上对于某些运算，计算机使用数学表得到一个近似的答案，然后执行计算去改进这个近似解。有些情况下，计算机背后的数学表是有误差的，最著名的就是最初的因特尔奔腾计算浮点除法使用的表。

对数表已经不像以前那么有用了，但它仍然是一个不错的迭代示例。下面这段程序在左边一栏输出一列值，在右边一栏输出其对应的一列对数值：

double x = 1.0;
while (x < 10.0) {
    cout << x << "\t" << log(x) << "\n";
    x = x + 1.0;
}

字符序列\t表示制表符。字符序列\n表示换行符。这些字符序列可以出现在字符串的任意位置，而在此例中，字符串中只有这类字符序列。

制表符使光标右移至制表结束位置，通常是每8字节制表一次。稍后我们将看到制表符的用途—使多列文本排列整齐。

换行符的作用与endl完全一样，即移动光标到下一行。通常情况，如果换行符单独出现，我就用endl；如果作为字符串的一部分出现，我就用\n。

上面一段程序的输出：

1     0
2     0.693147
3     1.09861
4     1.38629
5     1.60944
6     1.79176
7     1.94591
8     2.07944
9     2.19722

要是看着上面这些数很奇怪，别忘了log函数是以e为底的。计算机科学中2的幂很重要，因此我们常常要计算以2为底的对数，我们可以通过以下公式实现：

输出语句改为：

cout << x << "\t" << log(x) / log(2.0) << endl;

输出：

1    0
2    1
3    1.58496
4    2
5    2.32193
6    2.58496
7    2.80735
8    3
9    3.16993

可以看到，第1、2、4、8行为2的整数次幂。如果想求2的其他整数次幂，我们可以修改程序如下：

double x = 1.0;
while (x < 100.0) {
    cout << x << "\t" << log(x) / log(2.0) << endl;
    x = x * 2.0;
}

之前的循环中，我们用一个数去加x，输出一个算术序列；现在我们改用一个数去乘x，输出一个几何级序列。输出结果是：

1 0
2 1
4 2
8 3
16 4
32 5
64 6

由于我们在列之间使用的是制表符，所以第二列的位置也就不取决于第一列的数字位数了。

对数表也许不再有用，但对于和2的整数次幂打交道的计算机科学家而言，则是非常有用。下面出一道习题：修改上面这段程序，使之能一直输出到65536（2^16）。把程序打出来并记住它

6.5 二维表

二维表是这样一种表，可以在选定行和列后，读取行列交汇处的值。倍数表就是很好一例。假设你想打印1到6的倍数表。

开始写一个简单的循环，在一行打印2的倍数，是个不错的办法。

int i = 1;
while (i <= 6) {
    cout << 2*i << " ";
    i = i + 1;
}
cout << endl;

第一行初始化变量i，这是个计数器或循环变量。随着循环的执行，i从1增至6，当i增至7时，循环结束。每经历一次循环，我们就打印一个2*i的值，然后是3个空格。第一个输出语句不加endl，我们就把所有的值输出在一行上。

上面这段程序输出如下：

2   4   6   8   10   12

目前为止一切都好。下一步是封装和泛化。

6.6 封装和泛化

一般情况下，封装的意思是提取出一段代码，包装在一个函数里，这样使你能够在适合的地方使用此函数。我们已经看到过两个封装的示例：4.3小节的printParity函数和5.8小节的isSingleDigit。

泛化的意思是提取出特例的代码（如打印2的倍数），修改它使之更通用（如打印任意整数的倍数）。

下面的函数封装了前一小节的循环代码，并泛化为打印n的倍数。

void printMultiples (int n)
{
    int i = 1;
    while (i <= 6) {
        cout << n*i << " ";
        i = i + 1;
    }
    cout << endl;
}

封装要做的就是添加第一行代码，声明了函数名、参数和返回值类型。泛化要做的就是用参数n取代原来的2。

如果我们调用此函数时，给参数赋值为2，我们的输出就和之前一样。如果参数值为3，则输出为：

3 6 9 12 15 18

如果参数值为4，则输出为：

4 8 12 16 20 24

现在你大概可以猜到我们将怎样取打印乘法表：使用不同的参数值反复调用printMultiples。事实上我们将使用另一个循环来迭代打印各行。

int i = 1;
while (i <= 6) {
    printMultiples (i);
    i = i + 1;
}

首先要注意这个循环和printMultiples内部那个循环的相似之处。我所做的只是用一句函数调用取代打印语句。

这段程序的输出如下：

1 2 3 4 5 6
2 4 6 8 10 12
3 6 9 12 15 18
4 8 12 16 20 24
5 10 15 20 25 30
6 12 18 24 30 36

这就是一个（有点粗糙的）乘法表。如果你受不了这种粗糙，就请将列之间空格替换为制表符，看看输出什么。

6.7 函数

上一小节我曾提到“在适合的地方使用此函数”。现在可能你想知道究竟什么是适合的地方。下面就是函数有用的一些理由：

• 给一组语句起个名字，便于程序的阅读和调试。
• 把一段长程序分割为各个函数，便于分解程序，独立调试，然后整合为一个整体。
• 函数式递归和迭代变得方便。
• 设计良好的函数通常能用于许多程序。当你编写或调试一段程序时，可以重用函数。

6.8 再说封装

再说一说封装。我以上一小节的代码为例，将其封装成函数：

void printMultTable () {
    int i = 1;
    while (i <= 6) {
        printMultiples (i);
        i = i + 1;
    }
}

我阐述的是开发计划的常见流程。你通过向main函数或其它地方添加一行代码，一步步进行开发。当你的程序能运行了，你应该提出代码并封装为函数。

这个过程很有用，因为有时当你开始写程序时，并不能精确知道该怎么划分函数。此方法可以让你一边开发一边设计。

6.9 局部变量

现在你大概想知道我们要怎样在printMultiples和printMultTable两个函数中使用同一个变量i。我不是说过一个变量只能声明一次吗？函数改变了变量的值会不会出问题？

两个问题的答案都是“不”，因为printMultiples中的i和printMultTable中的i不是同一个变量。他们的名称相同，但不会指向同一块内存地址，因而改变其中一个值并不影响另外一个。

不要忘了函数内部声明的变量是局部的。你不能从局部变量的“宿主”函数外部访问此变量，而且你可以给多个变量起相同的名字，只要他们不在同一个函数内部。

这段程序的栈图清晰的表示出两个变量i并不占用同一块内存。他们有不同的值，改变一个并不影响另一个。

注意，printMultiples函数中参数n的值必须与printMultTable中i的值相同。另外，printMultiples中的i值从1增至n。图中i值为3，下一循环后将变为4。

在不同函数中使用不同变量名以避免混淆，这是个不错的主意，但重用名称也有很好的理由。例如用i、j、k命名循环变量是惯例。如果你在函数中避免使用这样的名字，仅仅因为你在别处用过了，这样你的程序将可能变得更难读。

6.10 再说泛化

另举一个泛化的例子：想象一下，你需要一个可以打印任意长度的乘法表，而不仅仅是6×6的表。你可以为printMultTable添加一个参数：

void printMultTable (int high) {
    int i = 1;
    while (i <= high) {
        printMultiples (i);
        i = i + 1;
    }
}

我用参数high替代6。如果我用参数值7调用printMultTable，我将得到输出：

1 2 3 4 5 6
2 4 6 8 10 12
3 6 9 12 15 18
4 8 12 16 20 24
5 10 15 20 25 30
6 12 18 24 30 36
7 14 21 28 35 42

一切很好，除了一点：我可能想让这个表变为方阵（行数和列数一样）。这意味着我需要为printMultiples添加另一个参数来指定表的列数。

絮叨几句，我也把这个参数命名为high，说明了不同函数可以有相同名字的参数（如同局部变量）：

void printMultiples (int n, int high) {
    int i = 1;
    while (i <= high) {
        cout << n*i << " ";
        i = i + 1;
    }
    cout << endl;
}

void printMultTable (int high) {
    int i = 1;
    while (i <= high) {
        printMultiples (i, high);
        i = i + 1;
    }
}

注意，当我添加一个新的参数，我必须改变函数的第一行（即接口或原型），同时必须修改printMultTable中调用函数的地方。正如所料，这段程序生成了一个7×7的方阵：

1 2 3 4 5 6 7
2 4 6 8 10 12 14
3 6 9 12 15 18 21
4 8 12 16 20 24 28
5 10 15 20 25 30 35
6 12 18 24 30 36 42
7 14 21 28 35 42 49

当你适当的泛化一个函数以后，你常常会发现程序的输出结果有一些意外的性质。比如，你可能注意到了，乘法表示对称的，因为ab=ba，所以表中所有的项都出现了两次。你可以只打印半张表以省墨。将

printMultiples (i, high);

改为

printMultiples (i, i);

你将得到输出：

1
2 4
3 6 9
4 8 12 16
5 10 15 20 25
6 12 18 24 30 36
7 14 21 28 35 42 49

至于其工作原理，就留给你分析了。

6.11 术语表

循环(loop)：当判断条件为真或者满足某些条件时，反复执行的语句。

无限循环(infinite loop)：判断条件始终为真的函数。

循环体(body)：循环内的语句。

迭代(iteration)：循环体从头至尾的一次执行，包括判断条件的求值。

制表符(tab)：一种特殊字符，C++用\t表示，该字符使当前行的游标移至下一个制表位置。

封装(encapsulate)：把大型复杂系统划分为各个组件（如函数），并使组件之间彼此隔离（比如使用局部变量）。

局部变量(local variable)：函数内部声明的变量，生存期仅在函数内部。局部变量不能从其所属函数外部访问，也不会与其它函数相互影响。

泛化(generalize)：用某些通用的量（如变量或参数）适当取代某些没必要特殊化的值（如常量）。泛化使代码更通用，更有机会重用，甚至有时更易写。

开发计划(development plan)：开发程序的过程。我在本章阐释了这样一种开发方式，其基础流程是：首先开发简单的代码，使之能做指定的事情，然后进行封装和泛化。

第7章 字符串那些事儿

7.1 字符串的容器

我们已经见过五种值类型——布尔、字符、整型、浮点型和字符串，但只介绍了四种变量类型——bool、char、int和double。我们还没有介绍将字符串保存到变量中和执行字符串操作的方法。

事实上，C++中有好几种可以保存字符串的类型。 其中一个是C++语言中的基本类型，有时称为“原生C字符串”。C字符串的语法有点儿丑陋，而且使用这种字符串要用到一些尚未介绍的概念，所以我们尽量避免使用它。

我们要使用的字符串类型是apstring，这是为计算机科学先修课程考试定制的类型【注1】。

不幸的是，完全避免C字符串是不可能的。本章有的地方我会就使用apstring代替C字符串可能遇到的问题给出一些警告。

你可能想知道类是什么。类的完整定义过几章我才会给出，现在读者可以认为类是函数的集合，其中函数定义了可以在类型上执行的操作。apstring类包含了所有可用于apstring变量的函数。

注1：为便于在书中讨论大学先修课程考试所用的类，我必须加入这段话： “Inclusion of the C++ classes defined for use in the Advanced Placement Computer Science courses does not constitute endorsement of the other material in this textbook by the College Board, Educational Testing service, or the AP Computer Science Development Committee. The versions of the C++ classes defined for use in the AP Computer Science courses included in this textbook were accurate as of 20 July 1999. Revisions to the classes may have been made since that time.”

7.2 apstring变量

读者可以以普通的方式创建apstring类型的变量。

apstring first;
first = "Hello, ";
apstring second = "world.";

第一行创建了一个apstring变量，没有赋初值，第二行将它赋值为字符串“Hello”。第三行结合了声明与赋值，也称作初始化。

一般而言，当像“Hello”或“world”这样的字符串出现时，它们被当作C风格的字符串。 即使如此，当把它们赋值给apstring变量时，它们被自动转换为apstring值。

我们可以以普通的方式输出字符串:

cout << first << second << endl;

为了编译这段代码，读者必须包含apstring类的头文件，并将apstring.cpp文件加入到要编译的文件列表中。 具体操作细节依赖于读者的编程环境。

在进入下一步之前，读者应该亲自敲入上面的代码并确保其可以编译和运行。

7.3 从字符串中提取字符

所谓字符串，指的就是字符的序列或者“串”。我们要在字符串上执行的第一个操作是提取所有字符中的一个。C++使用方括号（[和]）执行该操作：

apstring fruit = "banana";
char letter = fruit[1];
cout << letter << endl;

表达式fruit[1]表明我们要从字符串变量fruit中取得编号为1的字符，并将结果保存在字符变量letter中。当输出letter这个字符变量时，真奇怪：

a

a并非“banana”的第一个字母，除非你是计算机科学家。因为一些有悖常理的原因， 计算机科学家总是从0开始计数。“banana”的第0个字母是b，第1个字母是a，而第二个字母是n。

如果想取到字符串的第0个字母，必须将0放在方括号中，即：

char letter = fruit[0];

7.4 字符串长度

要求出字符串的长度（字符的个数），我们可以使用length函数。调用这个函数的语法和我们前面看到的有点不同：

int length;
length = fruit.length();

对于这种函数调用，我们称之为在字符串变量fruit上**调用（invoke）**length函数。“调用（invoke）”这个词可能看起来有点奇怪，但是后面我们还会遇到很多在对象上调用函数的例子。 函数调用的语法称为“点记号”，因为点（.）用以将对象fruit和函数length分隔开。

length函数不接受任何参数，这点可以从函数后面的空括号看出来。 它的返回值是一个整型数，上面例子中就是6。注意变量与函数同名是合法的。

要找到字符串的最后一个字母，你可能想这么做：

int length = fruit.length();
char last = fruit[length]; // 错误！！

这个不能正常执行，“banana”中没有第6个字母。因为我们从0开始计数，这6个字母编号为从0到5。要得到最后一个字母，应该将长度减1。

int length = fruit.length();
char last = fruit[length-1];

7.5 遍历

一种常见的字符串处理方法是，从字符串开头开始，依次选择每个字符并做一些处理，直到字符串的末尾。这种处理模式叫做”遍历“。一个自然的遍历方式是使用while语句：

int index = 0;
while (index < fruit.length()) {
  char letter = fruit[index];
  cout << letter << endl;
  index = index + 1;
}

该循环遍历字符串，并在一行中输出每个字母，也就是输出fruit自身。注意循环的条件是index < fruit.length()，当index等于字符串长度时，条件为假，循环体不会执行。循环中访问的最后一个字符的索引是fruit.length()-1。

循环变量的名字是index，即索引。索引是用来指定有序集中的一个成员的变量或值，例子中就是字符串的字符组成的集合。index指出我们想要哪一个。 集合必须是有序的，保证每个字母都有一个索引，并且每个索引都能找到特定的字符。

作为一个例子，请编写一个函数，该函数以apstring类型作为参数，在一行中逆向输出参数中的所有字母。

7.6 一个运行时错误

在1.3.2节我们谈到了运行时错误，这是直到程序启动运行之后才会出现的错误。

到目前为止，读者可能并未见过运行时错误，因为我们没做过可能导致运行时错误的事情。不过现在要遇到了。使用[]操作符时，如果提供了一个负的或大于总长度-1的索引值，就会出现运行时错误，并给出类似下面这种提示信息：

index out of range: 6, string: banana

请在你的开发环境中尝试一下，看看输出是什么。

7.7 find函数

apstring类还提供了其他几个可以在字符串上调用的函数。find函数的意义看起来与[]操作符相反。不同于接收索引值然后提取索引值对应的字符，find函数接收一个字符然后找到字符相应的索引。

apstring fruit = "banana";
int index = fruit.find(’a’);

上面例子的功能是找出字符串中字母‘a’的索引。在这个例子中，字母‘a’出现了三次，所以find该如何处理并不是显而易见的。根据文档，它返回第一次出现处的索引，所以结果是1。如果字符串中不存在给定字母，find函数返回-1。

此外，find还有一个版本，它接收另一个apstring作为参数，找到参数表示的子串在原字符串中出现位置的索引。例如：

apstring fruit = "banana";
int index = fruit.find("nan");

这个例子的返回值为2。

读者应该还记得，在5.4节中我们提到过可以存在多个同名函数，只要它们的参数数目或类型不同。这个例子中，C++可以根据提供参数的类型确定调用find的哪个版本。

7.8 我们自己的find版本

如果要在apstring变量中查找一个字符，可能我们并不想从字符串的头部开始查找。这种find函数的一种实现方式就是写一个增加一个参数的版本——传入我们希望的开始位置的索引。这是该函数的一个实现：

int find (apstring s, char c, int i)
{
  while (i<s.length()) {
    if (s[i] == c) return i;
    i = i + 1;
  }
  return -1;
}

不同于在apstring变量上调用find函数，如find的第一个版本那样，我们必须将apstring变量作为该find函数的第一个参数。其他参数分别是要查找的字符和开始查找的位置的索引。

7.9 循环与计数

下面程序计算字符串中字母‘a’出现的次数：

apstring fruit = "banana";
int length = fruit.length();
int count = 0;

int index = 0;
while (index < length) {
  if (fruit[index] == 'a') {
    count = count + 1;
  }
  index = index + 1;
}
cout << count << endl;

这个程序展示了一个叫做“计数器”的习惯用法。变量count初始化为0，每次找到一个‘a’时加1。退出循环时，count就是结果，即字符串中‘a’的个数。

作为练习，请将该代码封装到一个名为countLetters的函数中，该函数要以字符串和字母作为参数。

第二个练习，请重写该函数，要求该函数不能遍历字符串，而是使用我们前一节编写的find版本。

7.10 增量与减量操作符

因为增量和减量都是很常见的操作，所以C++为它们提供了专用操作符。++操作符的功能是将当前变量增加1，它支持int、char和double类型，而–操作符将当前变量减少1。这两个操作符都不能应用于apstring类型，也不能应用于bool类型。

从技术角度讲，增加一个变量的同时将它作为一个表达式是合法的。例如，你可能会看到这样的写法：

cout << i++ << endl;

看这个例子，增量发生在输出之前或者之后并不清楚。因为这种表达式令人困惑，所以不建议读者使用。 实际上，为了进一步阻止你使用它，我不会告诉你该语句的答案。如果想知道，请自行尝试。

我们可以使用增量操作符重写字符计数程序：

int index = 0;
while (index < length) {
  if (fruit[index] == 'a') {
    count++;
  }
  index++;
}

下面是一个常见错误：

index = index++; // 错误！！

很不幸，这在语法上是正确的，编译器不会给出警告。这个语句会导致index的值没被改变【译者注1】。这是个难以定位的bug。

记住，你可以写index = index +1;，也可以写index++;，但是不能将他们混到一起。

译者注1： index = index++; 的实现与编译器有关，原书这里的说法不是很准确。当然，这种写法肯定是要避免的。

7.11 字符串连接

有趣的是，+操作符可以用于字符串，它执行字符串连接操作。连接是指将字符串首尾相连。例如：

apstring fruit = "banana";
apstring bakedGood = " nut bread";
apstring dessert = fruit + bakedGood;
cout << dessert << endl;

这个程序的输出是： banana nut bread。

不幸的是，+操作符不能应用于原生C字符串上，所以不能编写这样的语句：

apstring dessert = "banana" + " nut bread";

因为所有的操作数都是C字符串。但是只要其中一个是apstring，C++就会自动的转换另一个。将一个字符连接到一个apstring变量的头或尾都是可以的。下面的例子中，我们会使用连接和字符算数来输出按字母顺序排列的序列。例如，在Robert McCloskey的《Make Way for Ducklings》一书中，小鸭子的名字分别是Jack,、Kack、Lack、Mack、Nack、Ouack、Pack和Quack.。这是一个按顺序输出这些名字的循环：

apstring suffix = "ack";
char letter = ’J’;
while (letter <= ’Q’) {
  cout << letter + suffix << endl;
  letter++;
}

程序的输出是：

Jack
Kack
Lack
Mack
Nack
Oack
Pack
Qack

当然，这并不是很正确，因为我拼错了“Ouack”和“Quack”。作为练习，请修改程序以修正这个错误。

再次提醒，一定要小心使用字符串连接，在应用apstring时可以使用，而在原生C字符串时不要使用。不幸的是，在C++中，像letter + "ack"这样的表达式在语法上是正确的，虽然它会产生奇怪的结果，至少在我的开发环境中是这样。

7.12 apstring是可变的

你可以通过将[]操作符放在赋值语句的左边每次修改apstring中的一个字母。例如：

apstring greeting = "Hello, world!";
greeting[0] = 'J’;
cout << greeting << endl;

输出是Jello, world!。

7.13 apstring是可比较的

所有可用于int和double类型的比较操作符同样适用于apstring类型。例如，如果想知道两个字符串是否相等，可以这样写：

if (word == "banana") {
cout << "Yes, we have no bananas!" << endl;
}

另一个有用的比较操作符可以将单词按字母顺序排列。如下：

if (word < "banana") {
  cout << "Your word, " << word << ", comes before banana." << endl;
} else if (word > "banana") {
  cout << "Your word, " << word << ", comes after banana." << endl;
} else {
  cout << "Yes, we have no bananas!" << endl;
}

需要注意的是，apstring类比较大小写字母的方式和人是不同的。所有的大写字母都在小写字母的前面。结果是：

Your word, Zebra, comes before banana.

解决此问题的一个常见方法是，在比较之前将字符串转换为标准格式，比如全部变成小写。下一节会介绍如何转换。 我不会给出更难的问题了，这会让程序认识到zebras不是水果。

7.14 字符分类

一般来说，检查一个字符并测试它是大写还是小写、是字母还是数字是有用的。C++提供了一组库函数用来执行这种分类操作。要使用这些函数，需要包含头文件ctype.h。

char letter = ’a’;
if (isalpha(letter)) {
  cout << "The character " << letter << " is a letter." << endl;
}

你可能期望isalpha的返回值是bool类型，但由于一些甚至我都不想考虑的原因，它的返回值实际是整型，如果参数不是字母那结果会是0，参数是字母时结果就是非0值。

这个奇怪现象并不像看起来这般不便，因为如例子所示，在条件中使用这种整型数是合法的，其中0被当做假，而非0值被当做真处理。

从技术上讲，这种事情是不允许的——整型数并不同于布尔值。尽管如此，C++允许不同类型间自动转换这个习惯是有用的。

其他字符分类函数包括isdigit（用以识别0~9之间的数字）、isspace（用以识别各种空白字符，如空格符、制表符、换行符）等等。其他如isupper和islower函数用以识别大小写字母。

最后，还有两个进行大小写转换的函数，它们是toupper和 tolower。它们都接收一个字符型的参数并返回转换后的字符。

char letter = ’a’;
letter = toupper (letter);
cout << letter << endl;

这段代码的输出是A。

作为练习，请使用字符分类与转换库编写apstringToUpper和apstringToLower函数，它们都接收一个apstring类型的参数，将参数中的所有字母都转换为大写或者小写，返回类型为void。

7.15 其他apstring函数

本章并未介绍所有的apstring函数，在15.2节和15.4节我们会再介绍c_str和substr两个函数

7.16 术语表

对象（object）：关联数据及操作数据的函数的组合。 到目前为止我们用过的对象有cout和apstring，其中cout是由系统提供的。

索引（index）：用来选择有序集中的一个成员（比如字符串中的一个字符）的变量或值。

遍历（traverse）：对集合中的每个元素进行迭代并执行类似的操作。

计数器（counter）：对某些事物进行计数的变量，通常初始化为0然后再增加。

增量（increment）：将变量的值加1。C++中的增量操作符是++。实际上，这也是C++这个名字的由来，它意味着比C好1。

减量（decrement）：将变量的值减1。C++中的减量操作符是–。

连接（concatenate）：将两个字符串首尾相连。

第8章 结构体

8.1 复合值

到目前为止，我们使用的大多数数据类型都表示单个值，如整型数，浮点数，布尔值。 从这种意义上说，apstring不同于那些数据类型，它们由更小的部件组成：字符。因此，apstring是复合类型的一个例子。

根据需要，我们可能想把一个复合类型当作单个的事物(或对象)，也可能想访问它的某部分(或实例变量)。这两种理解是有意义的。

对于用户创建自己的复合值，这也是很有用的。 C++为此提供了两种机制：结构和类。 我们从结构开始学习，并在第14章介绍类（它们之间没有太大的差别）。

8.2 Point对象

作为一个复合结构的简单例子，可以考虑数学中点的概念。在一个层面上，点是我们以之作为一个对象的两个数字，即坐标。在数学符号中，点用括号中以逗号分隔的坐标表示。例如，（0,0）表示原点，（x，y）表示该点从原点起向右x个单位，向上y个单位。

在C++中，点可以很自然地以两个double表示。那么，问题是如何把这两个值组合成一个复合对象或结构呢？答案是结构体定义：

struct Point {
   double x, y;
};

结构体定义出现在任何函数定义的外面，通常是在程序的开头（include语句之后）。

该定义表明，这个结构中体中有两个元素，分别命名为x和y。这些元素称为实例变量，原因我稍后将作出解释。

忘掉结构体定义末尾的分号是一种常见错误。在大括号之后放置一个分号可能很奇怪，但你会习惯的。

定义了新的结构体之后，就可以使用该类型创建变量了：

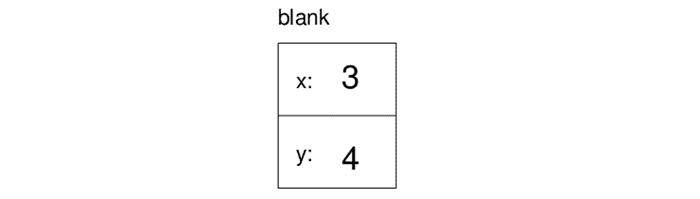
Point blank;
blank.x = 3.0;
blank.y = 4.0;

第一行是常见的变量声明：blank是Point类型。接下来的两行初始化结构体的实例变量。 这里使用的点记号与对象上调用函数的语法类似，如fruit.length()中的用法。当然,不同的是，函数名后面总是跟着一个参数列表，即使列表为空。

赋值的结果可以用下面的状态图表示：

照例，变量名blank在框外，而变量的值在框内。这里，这个值是一个复合对象，它由两个有名字的实例变量构成。

8.3 访问实例变量

你可以使用与写入实例变量值相同的语法来读取实例变量的值：

   int x = blank.x;

表达式blank.x表示“进入名为blank的对象中并取得x的值”。这里我们把这个值赋值给局部变量x。注意，名为x的局部变量和名为x的实例变量并不冲突。点号的作用就是明确地区分你所指的是哪一个变量。

可以将点记号用作C++表达式的一部分，所以下面代码是合法的：

  cout << blank.x << << ", " << blank.y << endl;
  double distance = blank.x * blank.x + blank.y * blank.y;

第一行输出为3, 4；第二行计算的结果是25。

8.4 对结构体的操作

大多数我们在其他类型上使用的操作符，例如数学运算符( +, %等)以及比较运算符（==，>等），都不适用于结构体。事实上，可以为这种新类型定义这些操作符的含义，不过在这本书中我们不会这么做。

另一方面，赋值运算符确实适用于结构。它可以用在两种方式上：初始化结构的实例变量或把实例变量从一个结构复制到另一个结构。一个初始化结构看起来像这样:

Point blank = { 3.0, 4.0 };

大括号里的值被依次赋给结构的实例变量。在这种情况下，x得到了一个值，y得到第二个值。

不幸的是，这个语法仅仅只能用在初始化中，而不能在赋值语句中。因此以下就是非法的。

Point blank;
blank = { 3.0, 4.0 };    // 错误!!

你可能想知道为什么如此完美合理的语句会是非法的；我不确定，但是我认为问题应该是编译器无法知道右边应该是什么类型。如果你添加一个类型定义：

Point blank;
blank = (Point){ 3.0, 4.0 };

这就可以了。

把一个结构赋给另一个结构是合法的。例如：

Point p1 = { 3.0, 4.0 };
Point p2 = p1;
cout << p2.x << ", " <<  p2.y << endl;

这个程序的输出是3, 4。

8.5 作为参数的结构

你能以通常做法把结构作为参数传递。例如:

void printPoint ( Point p) {
    cout << "(" << p.x << ", " << p.y << ")" << endl;
}

printPoint方法把一个point作为参数，并以标准格式将其输出。若调用printPoint(blank),则会输出(3,4)。

作为第二个例子，可重写5.2节的distance函数，以使它用两个Point类型变量作为参数，代替原来的四个double类型变量。

double distance (Point p1, Point p2) {
  double dx = p2.x - p1.x;
  double dy = p2.y - p1.y;
  return sqrt (dx*dx + dy*dy);
}

8.6 传值调用

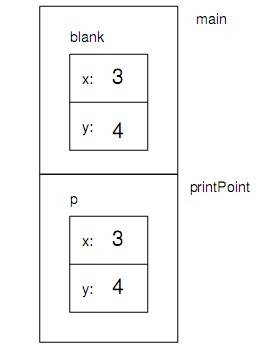
当你把一个结构作为实参传递时，请牢记实参和形参并非同一变量。而是最初有着相同值的两个变量(一个在调用者中，另一个在被调用者中)。比如，当调用printPoint时，栈图看起来会是这样：

如果printPoint改变了p的一个实例变量,blank并不会随之受到影响。当然，printPoint函数没理由去修改它的参数，因而两个函数之间的这种隔离是合适的。

这种类型的参数传递被称为"按值传递",因为传递给函数的是结构(或其他类型)的值。

8.7 传引用调用

C++中另一种可选择的参数传递机制被称为"传引用调用"。这种机制使得我们能传递一个结构体给程序并修改它。

例如，你可以通过交换两个坐标来得到某个点关于45度线的对称点。reflect函数最明显(但不正确)的写法是:

void reflect (Point p)     //错误!!
{
   double temp = p.x;
   p.x = p.y;
   p.y = temp;
}

这么写并不奏效，因为我们在reflect函数中所做的改变并不会影响调用者。

相反，我们必须指明要通过引用传递参数。为参数声明加上一个符号(&)即可。

void reflect (Point& p)
{
  double temp = p.x;
  p.x = p.y;
  p.y = temp;
}

现在我们以普通方式调用这个函数:

printPoint(blank);
reflect(blank);
printPoint(blank);

程序输出与预期相符:

(3,4)
(4,3)

下图展示了我们为程序绘制的栈图：

参数p是blank结构的一个引用。引用通常用一个带箭头的点表示，箭头指向引用所指。

图中最重要的是要看到：引用对p做的任何改变同样会影响blank。

通过引用传递结构比按值传递更通用，这是因为被调用者也能修改结构。此外，由于系统不需要复制整个结构，这使得引用传递更快。另一方面，它的安全性下降了，因为很难追踪结构是在哪被修改的。尽管如此，在C++程序中，几乎所有的结构都是按引用传递的。本书中我会遵循这一习惯。

8.8 矩形

现在假设我们要创建一个结构体来表示一个矩形。问题在于，我需要提供哪些信息来指定一个矩形?为了简化问题，我们假设矩形是垂直方向或水平方向的，没有倾斜角度。

存在几种可能：我可以指定矩形的中心(两个坐标)和大小(宽度和高度)，我也可以指定矩形的一个角和矩形的大小，或是指定两个相对的角。

现有程序中最常见的选择是指定矩形的左上角和大小。在C++中，我们定义一个结构，包含着一个Point类型和两个double类型。

struct Rectangle {
  Point corner;
  double width, height;
};

注意到一个结构中可以包含另一个结构。事实上这种情况很常见。当然，这意味着为了创建一个Rectangle，我们得先创建一个Point：

Point corner = { 0.0, 0.0 };
Rectangle box = { corner, 100.0, 200.0 };

这段代码创建了一个新的Rectangle结构并对实例变量进行了初始化。下图展示了这些语句的效果。

我们可以用普通的方式来存取width和height：

box.width += 50.0;
cout << box.height << endl;

为了访问corner的实例变量，我们使用了一个临时变量：

Point temp = box.corner;
double x = temp.x;

或者我们可以把两条语句组合在一起：

double x = box.corner.x;

这条语句最好是从右向左读： “从box的corner中抽取x，然后把它赋给局部变量x。”

当我们谈到组合时，我必须指出，实际上你可以同时创建Point和Rectangle：

Rectangle box = { { 0.0, 0.0 }, 100.0, 200.0 };

最里面的大括号中是点corner的坐标;它们组成了新的Regtangle中三个值中的第一个。这条语句是嵌套结构的一个例子。

8.9 作为返回值的结构

你可以写出返回结构的函数。如，findCenter函数把一个Rectangle类型作为参数，返回一个Point类型的值，其中包含着该矩形中心的坐标：

Point findCenter (Rectangle& box)
{
    double x = box.corner.x + box.width/2;
    double y = box.corner.y + box.height/2;
    Point result = {x, y};
    return result;
}

调用这个函数时，我们需要传入一个box作为参数(注意它是通过引用传递的),并把返回值赋给一个Point类型的变量:

Rectangle box = { {0.0, 0.0}, 100, 200};
Point center = findCenter (box);
printPoint (center);

程序输出(50,100)。

8.10 按引用传递其他类型

不单是结构能按引用传递，所有其他我们见过的类型同样可以。例如，我们可以这么写，来交换两个整数：

void swap (int& x, int& y)
{
   int temp = x;
   x = y;
   y = temp;
}

用普通方式调用这个函数:

int i = 7;
int j = 9;
swap (i, j);
cout << i << j << endl;

程序输出97。你可以为程序画出栈图来说服自己这是正确的。如果参数x和y声明为普通参数(没有加上&符号)，则swap函数无效。它会修改x和y，而对i和j没有影响。

当人们开始通过引用传递东西，例如整型时，他们经常试图使用表达式作为引用参数。如：

int i = 7;
int j = 9;
swap (i, j+1);            //错误！

这是不合法的，因为表达式j+1并不是一个变量—它并没有占据一个引用可以指向的地址。弄清楚什么类型的表达式可以传引用是一个小技巧。目前一个好的规则是引用参数必须是变量。

8.11 获取用户输入

目前为止，我们写的程序都是可预见的，它们每次运行时都做相同的事情。然而大多数时候我们需要程序能从用户那得到输入并随之做出反应。

有很多种方式可以得到输入，包括键盘输入，鼠标移动和按钮点击，此外还有更特别的机制，例如声控和视网膜扫描。本文我们只考虑键盘输入。

在头文件iostream.h中，C++定义了一个cin对象来处理输入，就像用cout对象处理输出一样。从用户那得到一个整型值可以这么写：

int x;
cin >> x;

操作符使得程序停止执行，等待用户输入。如果用户输入了有效值，程序会将它转换成整型值并存放在x中。

如果用户输入的不是整型，C++不会报告一个错误。相反，它把一些无意义的值存在x中并继续执行。

幸运的是，有一种方法可以检查输入语句是否成功。我们可以在cin上调用good函数来检验所谓的流状态。good方法返回一个布尔值：如果为真，则说明上一次的输入语句成功了。否则，我们知道之前的一些操作失败了，而且接下来的操作也会失败。

因此，从用户那得到输入看起来会像这样：

int main()
{
  int x;

  // 提示用户输入
  cout << "Enter an integer: ";

  // 获取输入
  cin >> x;

  //检查输入语句是否成功
  if(cin.good == flase) {
    cout << "That was not an integer." << endl;
    return -1;
  }

  //打印从用户处得到的值
  cout << x << endl;
  return 0;
}

cin也可以用于输入一个apstring：

 apstring name;

 cout << "What's your name? ";
 cin >> name;
 cout << name <<endl;

遗憾的是，这条语句只得到了输入的第一个单词，而把剩下的输入留给了下一条输入语句。所以，如果你运行这段程序并打下你的全名，它将只输出你的第一个名字。

正因为这些问题（无法处理错误和可笑的行为）,我完全避免使用>>操作符，除非我是从确定无误的源中读取数据。

作为替代方法，我在aspstring中使用了一个getline方法。

apstring name;

cout << "What is your name? ";
getline(cin, name);
cout << name << endl;

getline的第一个参数是cin，它是输入的来源。第二个参数是spstring的名字，用来存储结果。

getline读入整行输入直到用户敲打Return或Enter键。这对于输入包含空格的字符串来说是很有用的。

事实上，getline对于获取任何输入通常都有效。例如，若你想让用户输入一个整数，你可以输入一个字符串然后检查它是否是一个有效整数。如果是，你能把它转换成一个整数值。否则，你能输出一个错误信息并让用户再次输入。

为了将字符串转换成整数，你可以使用atoi函数，它定义在在头文件stdlib.h中。我们会在15.4节中讨论到它。

8.12 术语表

结构（structure）:数据集组合在一起，被当作一个单独的对象。

实例变量(instance variable):一个命名数据块，组成一个结构。

引用(reference):一个值，表示或指向一个变量或结构。在状态图中，引用以箭头的形式出现。

传值(pass by value):传递参数的一种方法。作为实参的值被复制到相应的形参中，但形参和实参占据着不同的位置。

传引用(pass by reference):传递参数的一种方法。形参是实参变量的引用。对形参的改变也会影响实参变量。

第9章 再谈结构体

9.1 Time结构体

我们定义一个数据类型称为Time，用于记录一天的时间，以此作为第二例自定义数据结构。小时、分、秒是构成时间的各种信息，这些都是结构体的实例变量。

第一步要决定每个实例变量的类型。小时和分应该是整型。这回我们搞个有趣的，把秒定义为double型，以便记录秒的小数部分。下面是结构体的定义代码：

struct Time {
    int hour, minute;
    double second;
};

我们可以按常规方式创建Time对象：

Time time = { 11, 59, 3.14159 };

此对象的状态图如下：

“实例”一词有时用于探讨对象的问题，因为每个对象都是某种类型的实例（或示例）。之所以称之为实例变量，是因为某种类型的每个实例都是该类型实例变量的一个备份。

9.2 printTime函数

定义新类型时，一个不错的方法是：编写函数以可读形式显示实例变量。例如：

void printTime (Time& t) {
    cout << t.hour << ":" << t.minute << ":" << t.second << endl;
}

如果给函数参数赋一个时间值，则输出为：11:59:3.14159。

9.3 对象函数

我将在后面几节阐述操作于对象的函数的几种可能的接口形式。对于某些操作，你有几种可能的接口形式可供选择，因而你应权衡每一种形式的利弊：

纯函数：对象与/或基本类型作为参数值，但是不改变对象本身。返回值要么是一个基本类型值，要么是函数内部创建的一个新对象。

修改函数：对象作为参数，并且会修改其中一部分或全部对象。通常返回值为空。

填充函数：空对象作为参数之一，由函数填充它。从技术角度讲，这也是一种修改函数。

9.4 纯函数

如果一个函数的返回结果只取决于参数值，并且没有像修改参数、输出一些值等副作用，那么就可认为此函数是纯函数。

下面这个after函数就是一例。此函数比较两个Time变量并返回一个布尔值并指出第一个操作数是否比第二个晚：

bool after (Time& time1, Time& time2) {
    if (time1.hour > time2.hour) return true;
    if (time1.hour < time2.hour) return false;
    if (time1.minute > time2.minute) return true;
    if (time1.minute < time2.minute) return false;
    if (time1.second > time2.second) return true;
    return false;
}

当两个时间相等时，函数返回什么？函数是否有适当的返回值？如果是你为此函数编写文档，你会专门提及这种情况吗？

另外一例是addTime函数，负责计算两个时间值之和。比如现在是9:14:30，你的面包机工作时间是3小时35分钟，你可以使用addTime函数来计算什么时候面包做好。

下面是此函数的一个草稿，不一定完全正确：

Time addTime (Time& t1, Time& t2) {
    Time sum;
    sum.hour = t1.hour + t2.hour;
    sum.minute = t1.minute + t2.minute;
    sum.second = t1.second + t2.second;
    return sum;
}

下面举一个使用该函数的例子。若currentTime为当前时间，breadTime为面包机做面包用的总时间，你就可以用addTime计算面包做好的时间了。

Time currentTime = { 9, 14, 30.0 };
Time breadTime = { 3, 35, 0.0 };
Time doneTime = addTime (currentTime, breadTime);
printTime (doneTime);

这段程序的输出为12:49:30，答案正确。另外，还有些例子的结果是不正确的。你能想出一个吗？

这个函数的问题在于它没有处理秒数或分钟数加起来超过60的情况。这种情况我们必须将多出的秒数“进位”到分钟，或者多出的分钟进位到小时。

下面是再次修改函数后的正确版本：

Time addTime (Time& t1, Time& t2) {
    Time sum;
    sum.hour = t1.hour + t2.hour;
    sum.minute = t1.minute + t2.minute;
    sum.second = t1.second + t2.second;
    if (sum.second >= 60.0) {
        sum.second -= 60.0;
        sum.minute += 1;
    }
    if (sum.minute >= 60) {
        sum.minute -= 60;
        sum.hour += 1;
    }
    return sum;
}

代码正确了，但也变长了。稍后，我将给出另一个解决方案，能大大简短代码。

这段代码给出了我们之前没见过的两个操作符：+=和-=，用于简洁的表示变量的增减。比方说，语句

sum.second -= 60.0;

和语句

sum.second = sum.second - 60;

是等价的。

9.5 const参数

你也许注意到了，函数after和addTime的参数都是传递引用。这俩函数是纯函数，不修改接受的参数值，因此我也可以传值。

传值的好处是调用函数和被调用函数都进行了适当的封装–其中一方的修改不可能影响另一方，除非影响了返回值

另一方面，传引用由于避免了参数的复制，往往更高效。除此之外，C++有一个优秀的特性叫做const，它能使引用参数和值参数一样安全。

如果你要编写一个函数，并不打算修改其参数，你就可以声明一个常量引用参数。语法如下：

void printTime (const Time& time) ...
Time addTime (const Time& t1, const Time& t2) ...

上面代码只包含了函数的首行。如果你告诉编译器你不打算修改参数，这种语法可以起到提醒作用。如果你试图改变参数，编译器会报错，至少会告警。

9.6 修改函数

当然，有时候你也想修改其中一个参数值。修改参数值的函数称为修改函数。

举个修改函数的例子：考虑这样一个函数increment，它给一个Time对象加上一定的秒数。此函数的草案代码如下：

void increment (Time& time, double secs) {
    time.second += secs;
    if (time.second >= 60.0) {
        time.second -= 60.0;
        time.minute += 1;
    }
    if (time.minute >= 60) {
        time.minute -= 60;
        time.hour += 1;
    }
}

第一行执行一条基本操作，余下代码处理特殊情况，我们以前也见过。

这个函数是正确的吗？如果参数secs的值比60大得多，会发生什么情况？那样的话，只减一次60是不够的；我们必须一直减下去，知道second的值小于60。我们可以用while语句替代if语句来实现之：

void increment (Time& time, double secs) {
    time.second += secs;
    while (time.second >= 60.0) {
        time.second -= 60.0;
        time.minute += 1;
    }
    while (time.minute >= 60) {
        time.minute -= 60;
        time.hour += 1;
    }
}

这种解决方案是正确的，但是不够高效。你能想到一个不需要迭代的解决方案吗？

9.7 填充函数

你有时能看到用另一种不同的接口（不同参数和返回值）实现addTime这样的函数。addTime函数不是在每次调用时都创建一个新对象，而是要求调用者提供一个“空对象”用以存储其结果。请将下述代码和之前版本做比较：

void addTimeFill (const Time& t1, const Time& t2, Time& sum) {
    sum.hour = t1.hour + t2.hour;
    sum.minute = t1.minute + t2.minute;
    sum.second = t1.second + t2.second;
    if (sum.second >= 60.0) {
        sum.second -= 60.0;
        sum.minute += 1;
    }
    if (sum.minute >= 60) {
        sum.minute -= 60;
        sum.hour += 1;
    }
}

此方法的一个优点是调用者可以选择重用同一个对象来重复执行一组加法操作。这样做可以带来一点效率的提升，但也够含糊，会引发小错误。绝大多数编程的情况，用一点运行时间换取大量调试时间还是值得的。

注意：前两个参数可以声明为const，第三个不行。

9.8 哪个最佳？

修改器和填充函数可以做的事，纯函数也可以做到。实际上有些所谓的函数式编程语言只支持纯函数。一些程序员认为，比起使用修改器来，使用纯函数开发程序更快且更不易出错。但是，有很多时候修改器是很方便的，也有很多情况下函数是程序效率是更低的。

总而言之，我推荐在能使用纯函数的时候尽量编写纯函数，在修改器有无法比拟的优势的情况下，再求助于修改器。此方法可称为函数式编程风格。

9.9 增量开发vs高屋建瓴

我在本章阐述了一种程序开发的方法，我称之为快速建原型及迭代完善。先编写一个能执行基本运算的草案（或原型），然后用几个案例进行测试，发现缺陷并修正之。

尽管此方法很有效，但也会使代码变得没有必要的复杂–因为要处理许多特殊情况，而且不可靠–因为你很难知道是否发现了所有的错误。

一种备案是高屋建瓴，对问题看得深入一点可使变成更加容易。对此案例的深入看法是：一个Time对象其实就是一个基为60的3位数！秒是个位，分钟是“60位”，小时是“3600位”。

当我们编写addTime和increment两个函数，我们实际上是在做以60为基数的加法，所以我们需要进位。

还有一种解决整个问题的备案，即把Time类型转换为double类型，它利用了这样一个事实：计算机已经能够做double型的算术。下面是一个将Time转换为double的函数：

double convertToSeconds (const Time& t) {
    int minutes = t.hour * 60 + t.minute;
    double seconds = minutes * 60 + t.second;
    return seconds;
}

现在我们需要的只是把double转换为Time的方法了：

Time makeTime (double secs) {
    Time time;
    time.hour = int (secs / 3600.0);
    secs -= time.hour * 3600.0;
    time.minute = int (secs / 60.0);
    secs -= time.minute * 60;
    time.second = secs;
    return time;
}

你可能需要想一想，才能相信我所使用的不同基数之间的转换技术是正确的。假设你已经想通了，我们就可以用这些函数来重写addTime：

Time addTime (const Time& t1, const Time& t2) {
    double seconds = convertToSeconds (t1) + convertToSeconds (t2);
    return makeTime (seconds);
}

比之前的版本精简了不少，证明其正确性也更加容易（按常规要假设其调用的函数是正确的）。给大家一个练习：用同样方法重写increment。

9.10 泛化

在某种程度上，基60和基10之间相互转换的难度比处理时间转换要大。基转换更抽象，直觉告诉我们直接处理时间更好。

但是，如果我们意识到可以把时间当做基60的数，并花时间来写一个转换函数（convertToSeconds和makeTime），我们的程序就会更简短、更易读、更易调试、更可靠。

此后添加更多特性也变得更容易。例如两个时间相减求时间差。最简单的做法是通过借位实现减法。使用转换函数将更容易做，且更不易出错。

具有讽刺意味的是，有时把问题变得更难（更具通用性）反而使其更易解决（更少特例，更少出错）。

9.11 算法

当你编写一个针对一类问题的通用解法，而非针对某一个问题的特定解法时，你就写出了一个算法。我在第一章提到过这个词，但是没有给出详细定义。这也不太好定义，所以我会试用多种方式进行定义。

首先，考虑一些不是算法的问题。当你学习个位数乘法时，你可能会背乘法表。实际上你记住的是100个特定解法，这种知识并不是真正意义的算法。

但是，如果你很“懒”，你可能学习一些作弊技巧。比如，求n与9的乘积，你可以在第一位上写n-1，第二位上写10-n。这一技巧是9与任意个位数相乘的通用解法。这就是一个算法了！

类似地，你学过的进位加法、借位减法、长除法等等这些技术都是算法。算法的特点之一是执行时无需任何智能性。算法是机械过程，按照一组简单的规则，一步接一步的执行。

我认为，人们花那么多时间在学校学习死板的执行算法，无需任何智慧，这实在令人尴尬。

另一方面，算法的设计过程是有趣的，挑战智慧，这才是所谓的编程的核心部分。

一些人们在自然而然状态下做的事情，没有任何难度或下意识地思考，但这才是最难用算法表达的事情。自然语言理解就是很好的例子。我们都在做这件事，但迄今为止没人能解释该怎么做，至少不能以算法的形式给出解释。

稍后在本书中我将有机会针对许多问题设计简单的算法。如果你选修了计算机科学专业的下一门课数据结构，你将看到计算机科学所带来的一些最有趣、最聪明、最有用的算法。

9.12 术语表

实例(instance)：某个种类的一个示例。例如，我的猫猫就是“猫科动物”种类的一个实例。每个对象都是某种类型的一个实例。

实例变量(instance variable)：组成结构体的命名数据项之一。对于属于结构体类型的各个实例变量，每个结构体都有一份属于自己的备份。

常量引用参数(constant reference parameter)：通过引用传递但不可修改的参数。

纯函数(pure function)：输出结果只取决于输入参数的函数，这种函数除了返回新值之外，不起任何副作用。

函数式编程风格(functional programming style)：一种程序设计风格，大部分函数是纯函数。

修改函数(modifier)：一种能修改一个或多个参数并往往没有返回值的函数。

填充函数(fill-in function)：一种以空对象为参数并填充此实例变量而非返回新对象值的函数。

算法(algorithm)：一组通过机械式、非智能过程来解决某一类问题的指令。

第10章 向量

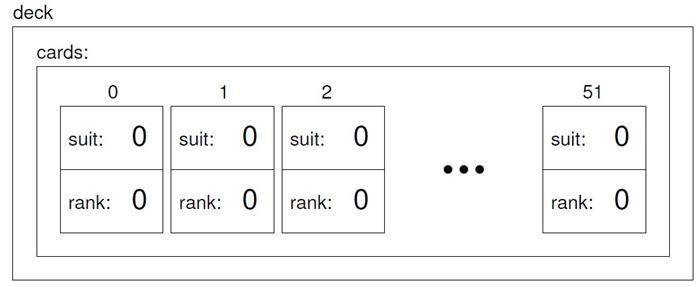
10.1 元素访问

[ ]操作符可以对向量进行读和写，这和apstring访问字符类似。同样和apstring一样，索引从0开始，count[ 0 ]指的是向量中的第0个元素，count[ 1 ]指的是向量中的第1个元素。[ ]操作符可以应用在任何表达式中。

count[0] = 7;
count[1] = count[0] * 2;
count[2]++;
count[3] -= 60;

所有的这些语句都是合法的赋值语句。下图是这些代码段的效果：

Count

10.2 向量的复制

apvector还有一个构造函数，我们称之为复制构造函数。因为它使用一个apvector作为参数来创建一个新的向量，这个新的向量的类型与元素都和原来的向量相同。

apvector<int> copy (count);

虽然这个语句是合法的，但我们几乎从来不用它来创建apvector，因为还有一种更好的方式：

apvector<int> copy = count;

“=”操作符用在apvector上的工作方式和你想得差不多。

10.3 for循环

到现在为止我们所写的循环都有一些共同的元素。它们都是以初始化一个变量开始；它们有一个基于这个变量的测试或者条件语句。在循环体里对这个变量做一些操作，例如增加变量的值。

这类循环如此常见，以至于有一个针对这种情况的可选的循环语句，即for循环，for循环可以使表达更为简洁。通常写法如下：

for (初始化; 条件语句; 增量) {
    循环体
}

除了更为简洁之外（因为for循环把所有循环相关的语句放到了一起，这样代码更易读），这些语句与下面的while循环语句等价：

初始化;
while (条件语句) {
    循环体
    增量
}

这是一个例子：

for (int i = 0; i < 4; i++) {
    cout << count[i] << endl;
}

它与下面的while循环等价。

int i = 0;
while (i < 4) {
    cout << count[i] << endl;
    i++;
}

10.4 向量的长度

这里有几个函数可以让你在apvector中调用。其中一个是非常有用的，就是：length。显而易见的，它返回的是向量的长度（元素的个数）。

这比使用一个静态量用来确定循环的上限更好。使用这个方式，即使你的向量发生改变，你也不需要去修改你程序的循环语句。它们会在任何的向量中准确的工作着。

for (int i = 0; i < count.length(); i++) {
    cout << count[i] << endl;
}

最后一次的循环体被执行，i的值就等于count.length() - 1, 这指向最后一个元素。当i等于count.length() 时，条件语句为假，循环体不会被执行，这是一件好事，如果不这样它会导致发生一个运行时错误。

10.5 随机数

大多数计算机程序在执行的时候做着同样的事情，所以它们被称作确定性的。通常，确定性是一个好处，我们都期望计算产生相同的结果。例如某些程序，我们却希望计算机不准确。游戏是一个显著的例子。

写一个真的不确定的程序似乎没那么容易，但是有些许方法至少可以产生看起来比较不确定的结果。其中一个就是生成伪随机数来决定程序的输出。伪随机数不是真正数学意义上的随机，但我们为了达到目的，我们必须这么做。

C++提供一个函数叫做random用于生成随机数。它被声明是stdlib.h头文件中，这个文件包含了各种各样的“标准库”函数，所以取了这个名字。

从random返回是值是一个在0到RAND_MAX之间的整型数，RAND_MAX是一个非常大的数字（在我的计算机里大约是20亿）当然，它也是定义在头文件中。你每一次调用random时，你都会得到一个不同的随机生产的数值。看下面的一个例子，运行在一个循环中：

for (int i = 0; i < 4; i++) {
    int x = random ();
    cout << x << endl;
}

在我在我的机器上得到以下的输出：

1804289383　　　846930886　　　1681692777　　　1714636915

你可能会得到一些类似，但在你的计算机上是会得到不同的结果。

当然，我们不希望得到一个巨大的整型数。更多的情况我们想生成一个从0到我们所规定的上限值之间的整型数。一个简单的方法就是使用求模运算。例如：

int x = random ();
int y = x % upperBound;

y是x对upperBound求模余数，y的值只能是在0到upperBound-1之间，包括两端的值。记住，y无论怎样都不会等于upperBound。

它通常也频繁用作生成随机浮点数。一个常见的方法是出于RAND_MAX。例如：

int x = random ();
double y = double(x) / RAND_MAX;

这些代码将使y的随机值在0.0到1.0之间，包括两端的值。作为一个练习，你可能会思考如何生成一个随机浮点数在给定的范围中。例如在100.0到200.0之间。

10.6 统计

使用random生产的随机数应该是均匀分布的。这意味着每一个值的出现是同样的概率。如果我们统计每个值出现的次数，在生成足够多的数值的情况下，所有的值出现次数将会大约得到一个相同的值。

在接下来几个段落中，我们将会写一个随机数序列并检查它是否符合这样的属性。

10.7 随机数的向量

第一步是生成大量的随机数并存储它们在一个向量中。“大量”我指的是20个。在开始应该使用一个可控范围的数值，这将有益于调试，之后在增加它的规模。

接下来的函数将会使用一个参数，用来表示向量的长度。它用于申请分配一个新的向量用作存储int型数据，并且用0至upperBound-1之间的随机数填充。

apvector randomVector (int n, int upperBound) { apvector vec (n); for (int i = 0; i,这意味着该函数返回一个整型数的向量。为了测试这个函数，这里有一个十分方便的函数用作输出向量中的内容。

void printVector (const apvector<int>& vec) {
     for (int i = 0; i<vec.length(); i++) {
        cout << vec[i] << " ";
    }
}

注意，这是一个apvector的合法语句参考。实际上它是十分常见的，因为它不必复制向量。因为printVector不需要修改向量，我们声明为const参数。

接下来的代码是生成一个向量并输出：

int numValues = 20;
int upperBound = 10;
apvector<int> vector = randomVector (numValues, upperBound);
printVector (vector);

在我的机器上输出是：

3 6 7 5 3 5 6 2 9 1 2 7 0 9 3 6 0 6 2 6

这看起来是十足的随机。你的输出结果可能不同。

如果这些数字真的是随机的，我们其他每一个数字出现都是同样的次数——每个两次。实际上，数字6出现了5次，4和8则未曾出现。

这是否意味着平均值不是很均匀？这很难说。只用几个数值，得到我们所期望结果的是十分渺茫的。随着数字的增多，输出将会更接近我们预期的。

为了测试这个理论，我们写一些程序用作统计每个数字出现的次数，当增加到numValues.之后再观察发生了什么。

10.8 计数

寻找解决这类问题的方法，首先可以从设计一些功能简单易运行的函数入手，每一个成功运行的简单函数对于解题都是有帮助的。一步步的设计，最后综合起来得到解决问题的方法。这就是所说的自底向上的程序设计方法。当然，想预先知道哪些函数对于程序设计有帮助，对于初学者来说还是比较困难的，随着经验的积累到一定的程度，你才会得心应手。

同样，由于经验的缺失，有时候我们并不能知道到底要写什么样的函数，这时我们就需要找到程序中有过类似解决经验的子问题，先把它们解决。

在7.9里，我们介绍了一个可以从一串字符中统计给定字符出现次数的函数。我们可以把这个函数作为一个“遍历和计数”的模型。这个模型的主要构成元素有：

• 一个可遍历的集合或容器，类似于字符串或向量。
• 一个可以应用到每个元素用于测试的语句。
• 一个统计已通过遍历元素个数的计数器。

在这里，我预先准备了一个叫做“howMany”的函数，用以统计向量中等于给定数值的数出现的次数。所需要的参数就只有向量值和给定整数的值。函数的返回值就是给定整数值出现的次数。

int howMany (const apvector<int>& vec, int value) {
    int count = 0;
    for (int i=0; i< vec.length(); i++) {
        if (vec[i] == value) count++;
    }
    return count;
}

10.9 检查其他值

函数“howMany”只是统计了某个特殊的数值的出现次数，有时候我们需要统计每个数值出现的次数。可以用下面这个循环函数完成这项工作。

int numValues = 20;
int upperBound = 10;
apvector<int> vector = randomVector (numValues, upperBound);

cout << "value\thowMany";

for (int i = 0; i<upperBound; i++) {
    cout << i << ’\t’ << howMany (vector, i) << endl;
}

注意这一点，在for语句中是可以定义变量的。这种语法设计有时候是很方便的，但是在循环语句中定义的变量只能在循环体中使用，这点要记住。比如，跳出循环后，变量i就不能再使用了。如果你尝试在循环体外面引用i，你将会得到一个编译错误。

这段代码使用了一个循环变量作为howMany函数的参数，以此按顺序统计每个数值的出现次数。程序运行的结果为：

Value     howMany
  0         2
  1         1
  2         3
  3         3
  4         0
  5         2
  6         5
  7         2
  8         0
  9         2

现在看来，我们还是不能说明随机数产生的几率是一样的。如果我们把数值出现的上限调到100000，将得到如下结果：

Value     howMany
0         10130
1         10072
2         9990
3         9842
4         10174
5         9930
6         10059
7         9954

对于每个数说，它们出现的次数误差在估计值的1%以内，由此我们可以认为随机数是均匀分布的。

10.10直方图

从之前的数据表取出并存储，在使用时可以直接调用，这个方法通常很有用，也比直接将数值打印出来要好。我们需要一个将十个整型数存储起来的方法。当然，我们可以定义十个整型变量，分别取名为howManyones，howManytows等，但是那样的话工作太过繁杂。而且当我们需要改变统计的数值个数时将很会麻烦。

因此，最好是使用一个长度为10的整型指针。这样的话，我们就可以一次完成十个整数值存储点的设置，并且可以使用数组索引到每个数值。程序如下：

int numValues = 100000;
int upperBound = 10;
apvector<int> vector = randomVector (numValues, upperBound);
apvector<int> histogram (upperBound);

for (int i = 0; i<upperBound; i++) {
    int count = howMany (vector, i);
    histogram[i] = count;
}

我把这个程序称作直方图，因为这是一个统计学上的名词，专门为向量中统计不同数值出现的次数而设计的。

这里一个很巧妙的地方是，循环变量在函数中得到了两次不同功能的使用。首先，它是howMany函数的参数，这正是我们想要统计的值。其次，它是向量统计图的索引值，将每个统计值存入对应存储点中。

10.11一次遍历的方案

虽然上面的函数可以完成指定工作，但是它的效率比较低。每一次调用howMany函数时它都要将整个数据内容遍历一次。在下面的程序中，我们需要将数据遍历十次。

我们要设计一个函数，使其将数据遍历一边就能完成工作。对数据中的每一个值，我们可以将其对应的计数存储点找出，并将其自增一。换句话说，我们使用向量中的值作为直方图的下标。下面是对应方法设计的程序：

apvector<int> histogram (upperBound, 0);

for (int i = 0; i<numValues; i++) {
    int index = vector[i];
    histogram[index]++;
}

第一行对统计值进行初始化直方图的值为0。通过这样，我们就可以在循环体里通过++操作符进行对直方图增长。我们知道我们让它会从0开始。而忘记初始化计数器是一个常见的错误。

作为一练习，可以将以上的代码封装设计好，组合成一histogram函数，输入一个向量并统计值范围（这里是0到10），返回值就是向量中的统计直方图。

10.12随机种子

当你将本章节的程序运行了几遍后，你就会发现，我们所得到的随机数值都是一样的。很明显，他们不是所谓的随机出现的。

伪随机数出现的特性之一是如果一连串随机数出现的起始点一样，则这一串数字始终是一样的。随机数出现的起始点称作种子。每次运行C++程序时，它默认将随机数种子保持一致。

当你调试程序时，产生相同的序列对你是非常有用的。当你修改程序时，就可以有一个更好的比对。

如果你想换一组随机数，可以使用srand函数。它只需一个参数，这个函数会取一个从0到RAND_MAX的随机数。

在许多的程序中，比如说游戏，我们希望每次运行游戏时都能得到不同的随机数列。通常的方法是使用如gettimeofday这样的库函数来获取可信的、不可预料及不重复的随机数作为种子，有如最后一秒里面的毫秒数值作为随机数种子。操作的细节取决于你的开发环境。

10.13术语表

向量（vector）：一连串具有相同类型的数值集合，每个值可以通过索引进行访问。

元素（elements）：向量中的一个值，可以通过[ ]操作符选择向量中的元素。

索引（index）：用于确定向量中元素的整型数变量或整型值。

构造函数（constructor）：用于创建新对象并初始化实例变量的特殊函数。

确定性（deterministic）：程序每一次运行的效果都是一致的。

伪随机（pseudorandom）：一个随机出现的数字序列，但事实上是由可确定的运算方式生成的。

随机数种子（seed）：用作初始化随机数序列的变量。使用相同是随机数种子将会产生相同的序列。

自底向上设计（bottom-up design）：一种编程的方式，从一个很小、很常用的函数开始写，最后再组合它们用作解决更大问题。

直方图（histogram）：一个包含整型数的向量，其中每个整型数用于统计特定范围内值的个数。

第11章 成员函数

11.1 对象和函数

通常认为C++是一种面向对象编程语言，这意味着它提供了支持面向对象编程的特性。

定义面向对象语言并非易事，但是我们已经看到了它具备的一些特性：

1.程序由一些结构定义和函数定义组成，大多数函数操作特定类型的结构(或者对象)。

2.每个结构定义对应着一些现实世界中的物体或概念，对结构进行操作的函数对应着现实世界中物体交互的方式。

例如，我们在第九章中定义的Time结构体明显对应着人们记录每天时间的方式，而我们定义的操作对应着人们记录时间所做的事情。类似地，Point和Rectangle结构体对应于数学概念上的点和矩形。

然而，迄今为止，我们还没有利用C++提供的支持面向对象编程的特性。严格来说，这些特性并非必要。在很大程度上，它们为我们所做的事情提供了另一种语法，但在许多情况下，这种语法能更加简明和精确地传达程序的结构。

如Time程序中，结构体定义和函数定义没有明显的联系。通过一些研究发现,每个函数显然应当至少将一个Time结构体作为参数。

这种观察结果是成员函数的动机。成员函数区别于另外我们写过的另两种函数：

1.调用函数时，我们不是直接调用，而是通过对象调用它。人们通常将这种过程描述成“对一个对象执行操作”或者“给一个对象发送消息”。

2.函数在结构体定义中声明，以使结构和函数之间的关系更加明显。

在后面几节中，我们会从第九章中拿出一些函数，并把它们转化成成员函数。你应该意识到这种转换是纯机械的。话句话说，你只需遵循一系列步骤就能完成。

如我所说，任何成员函数能做的事情，也能用非成员函数(有时称为独立函数)完成。但有时其中一种会优于另一种。如果你能很自然地从一种形式转换到另一种，那么你就能为你做的事情选择最好的形式。

11.2 print

在第9章中，我们定义了Time结构体并写了一个printTime函数

struct Time {
  int hour, minute;
  double second;
}

void printTime(const Time& time) {
  cout << time.hour << ":" << time.minute << ":" << time.second << endl;
}

要调用这个函数，我们需要传递一个Time对象作为参数。

Time currentTime = { 9, 14, 30.0 };
printTime(currentTime);

为把printTime转变为成员函数，第一步要将函数名由printTime改成Time::print。::操作符使结构体名字和函数名分离开，它们同样表明print函数能在Time结构体上调用。

下一步是消去参数。我们将在对象上调用这个函数，而不是将对象作为实参传递给函数。

因此，在函数中，我们不再有一个time参数，取而代之的是**当前对象，**即函数在这个对象上调用。可以使用C++关键字this来引用当前对象。

有一件难以理解的事情是，这里的this实际上是一个指向结构的指针，而不是结构本身。指针和引用类似，但现在我还不想讨论指针使用的细节。我们现在唯一需要的指针操作符是*操作符，它把一个结构体指针转化成结构体，在如下函数中，我们用它把this的值赋给局部变量time。

void Time::print() {
  Time time = *this;
  cout << time.hour << ":" << time.minute << ":" << time.second << endl;
}

当我们把函数转变成成员函数时，函数的前两行改变了不少，但是请注意输出语句完全没有变化。

为了调用新版的print，我们需要在一个Time对象上调用它:

Time currentTime = { 9, 14, 30.0 };
currentTime.print();

转变过程的最后一步是在结构体定义中声明这一函数:

struct Time {
  int hour, minute;
  double second;

  void Time::print ();
};

除了在行尾有一个分号以外，函数声明看起来很像函数定义的第一行。声明描述了函数的接口，也即参数数目和类型，以及返回值的类型。

声明一个函数的同时，也是在向编译器承诺你将在程序中提供函数定义。这里的定义有时也被称为函数的实现，因为它包含了函数工作的细节。如果你遗漏了定义，或者提供的函数的接口与你承诺的不同，编译器会抗议的。

11.3 隐式变量访问

其实新版的Time::print并不需要这么复杂。我们并非真的需要创建局部变量来引用当前对象的实例变量。

如果函数引用hour,minute或者second时，只写它们本身，而不写点号，C++知道它指的是当前对象。所以我们本可以这么写：

void Time::print()
{
   cout << hour << ":" << minute << ":" << second <<endl;
}

这种变量访问方式称为“隐式变量访问”，因为对象名没有显式地出现。这种特性是成员函数往往比非成员函数更简洁的一个原因。

11.4 另一个例子

我们来把increment函数转换为成员函数。我们再次将其中一个参数变成this。然后检查整个函数并使所有变量被隐式访问。

void Time::increment (double secs) {
  second += secs;

  while (second >= 60.0) {
     second -= 60.0;
     minute += 1;
  }
  while (minute >= 60.0) {
     minute -= 60.0;
     hour += 1;
  }
}

顺便说一句，请记住这并非是该函数的最高效实现。如果你在第九章没有这么做，那你现在应该写一个更有效率的版本。

我们可以复制第一行到结构体定义中来声明这一函数。

struct Time {
   int hour, minute;
   double second;

   void Time::print();
   void Time::increment(double secs);
}；

为了调用(call)这函数，我们再次需要通过Time对象调用（invoke）它：

Time currentTime = { 9, 14, 30.0};
currentTime.increment (500.0);
currentTime.print ();

程序输出9:22:50。

11.5 再一个例子

最初版本的convertToSeconds函数是这样的：

double convertToSeconds (const Time& time) {
  int minutes = time.hour * 60 + time.minute;
  double seconds = minutes * 60 + time.second;
  return seconds;
}

我们可以很直接的将其转换为成员函数：

double Time::convertToSeconds () const {
  int minutes = hour * 60 + minutes;
  double seconds = minutes * 60 + second;
  return seconds;
}

有趣的是，因为我们在函数中没有修改隐式参数，这里它应该被声明为const。但是，与不存在的参数相关的信息应该写在哪里并不是显而易见的。答案是——如例子所示——将const放在参数列表之后（本例中为空）。

上节中的print函数同样应该将其隐式参数声明为const。

11.6 更复杂的例子

尽管函数转换成成员函数的过程是机械式的，但还是有一些古怪的地方。例如，after函数对两个Time对象进行操作，而不仅仅是一个，我们不能使它俩都成为隐式的。而需要在其中一个对象上调用这个函数，并把另一个对象作为参数传递给它。

在函数中，我们隐式地引用其中一个对象，而继续使用点符号来访问另一对象的实例变量。

bool Time::after (const Time& time2) const{
    if(hour > time2.hour) return true;
    if(hour < time2.hour) return false;

    if(minute > time2.minute) return true;
    if(minute < time2.minute) return false;

    if(second > time2.second) return true;
    return false;
}

调用此函数：

if (doneTime.after (currentTime)) {
     cout << "The bread will be done after it starts." <<endl;
}

调用过程可以这么理解： “如果done-time在current-time之后，那么…”

11.8 初始化还是构造？

之前我们使用大括号声明并初始化了一些Time结构：

Time currentTime = { 9, 14, 30.0 };
Time breadTime = { 3, 35, 0.0 };

现在，通过使用构造函数，我们能用另一种方式来声明和初始化：

Time time (seconds);

这两个函数展现了不同的编程风格，以及在C++历史上不同的观点。可能是出于这个原因，C++编译器要求你使用其中一个，而不能在一个程序中同时使用。

如果你为结构体定义了一个构造函数，那么你需要使用构造函数来初始化该类型的所有新的结构。不再允许使用花括号的那种语法。

幸运的是，使用重载函数的方式来重载构造函数是合法的。换句话说，可以存在多个构造函数具有相同的"名字"，只要它们的参数不同就行。当我们初始化一个新的对象时，编译器会尝试找到具有合适参数的构造函数。

例如，一个构造函数为每个实例变量

Time::Time (int h, int m, double s)
{
    hour = h;   minute = m;   second = s;
}

我们使用以前的语法来调用这个构造函数，特殊之处在于形参需要两个整型数和一个double类型的数：

Time currentTime (9, 14, 30.0);

11.7 构造函数

我们在第九章中写的另一个函数是makeTime：

Time makeTime (double secs) {
    Time time;
    time.hour = int (secs / 3600.0);
    secs -= time.hour * 3600.0;
    time.minute = int (secs / 60.0);
    secs -= time.minue * 60.0;
    time.second = secs;
    return time;
}

当然，我们要能够为每种新类型创建新的对象。事实上，像makeTime这样的函数是如此普遍，以至于有一种针对它们的特殊函数语法。这些函数被称为构造函数，语法看起来是这样的:

Time::Time (double secs) {
    hour = int (secs / 3600.0);
    secs -= hour * 3600.0;
    minute = int (secs / 60.0);
    secs -= minue * 60.0;
    second = secs;
}

首先，注意到构造函数名字和类名相同，没有返回类型。而参数并没有改变。

其次，请注意我们并不需要创建一个新的time对象，也不需要返回任何东西。这两步都是自动处理的。我们可以使用关键字this或者此处使用的隐式方式来引用新对象----我们构造的那个对象。当我们给hour，minute，second写入值时，编译器知道我们引用的是新对象的实例变量。

我们使用介于变量声明和函数调用之间的语法来调用此构造函数：

Time time (seconds);

这条语句声明了一个Time类型的变量time，并调用我们刚写的构造函数，把seconds的值作为参数传递给构造函数。系统为新对象分配空间，而构造函数初始化了它的实例变量。结果赋给了变量time。

11.9 最后一个例子

最后一个例子是addTime：

Time addTime2 (const Time& t1, const Time& t2) {
   double seconds = convertToSeconds (t1) + convertToSeconds (t2);
   return makeTime (seconds);
}

我们要对该函数做一些改变，包括：

1. 把函数名addTime改成Time::add。
2. 把第一个参数替换成隐式参数，并将它声明为const。
3. 把原来的makeTime改成构造函数调用。

结果如下:

Time Time::add (const Time& t2) const {
   double seconds = convertToSeconds () + t2.convertToSeconds ();
   Time time(second);
   return time;
}

第一次调用convertToSeonds时，没有显式的对象！在一个成员函数中，编译器假设我们要在当前对象上调用函数。因此，第一次是在this上调用，第二次是在t2上调用。

函数接下来一行调用了构造函数，把单个double值作为参数。最后一行返回结果对象。

11.10 头文件

在结构体定义中声明函数，稍后再定义函数，这看起来是一件麻烦事。任何时候你要改变一个函数的接口，都需要在两个地方做修改，即使只是做了很小的变动，比如把一个参数声明为const。

尽管如此，这种麻烦是有理由的，我们能够把结构体定义和函数分离到两个文件中：头文件包含着结构体定义，而实现文件包含着函数。

头文件通常和实现文件同名，但后缀是.h而不是.cpp。对于我们一直看的例子，头文件名为Time.h，它包含以下内容：

struct TIme {
    // 实例变量
   int hour, minute;
   double second;

   //构造函数
   Time (int hour, int min, double secs);
   Time (double secs);

  //修改器
   void increment (double secs);

  //函数
   void print () const;
   bool after (const Time& time2) const;
   Time add (const Time& t2) const;
   double convertToSeconds () const；
};

请注意，我们并不需要在结构体定义中给每个函数名前面包含前缀Time::。编译器知道我们声明的函数是Time结构体的成员。

Time.cpp包含了成员函数的定义(为节省篇幅，我已经省去了函数体):

#include 
#include "Time.h"

Time::Time (int h, int m, double s)  ...

Time::Time (idouble secs)  ...

void Time::increment ( double secs)  ...

bool Time::after (const Time& time2) const ...

Time Time::add (const Time& t2) const ...

double Time::convertToSeconds () const ...

在本例中，Time.cpp中的定义与Time.h中声明的顺序相同，这并非必要。

另一方面，有必要使用include语句将头文件包含进来。这样一来，当编译器读取函数定义时，它能足够了解结构体，便于检查代码并捕获错误。

最后，main.cpp包含了函数main，以及我们需要的非Time结构体的成员的函数(本例中没有)：

#include 
#include "Time.h"

void main()
{
  Time currentTime (9, 14, 30.0);
  currentTime.increment (500.0);
  currentTime.print ();

  Time breadTime (3, 35, 0.0);
  Time doneTime = currentTime.add (breadTime);
  doneTime.print ();

  if (doneTime.after (currentTime)) {
      cout << "The bread will be donw after it starts." <<endl;
  }
}

再一次，main.cpp必须包含头文件。

把如此小的程序分成三部分的好处也许并不明显。其实，大部分优点会在我们处理更大的程序时体现出来:

重用：当你写了个类似于Time的结构，你也许会发现它在多个程序中都有用。通过把Time的定义从main.cpp中分离出来，在其它程序中包含Time结构会变得容易。

管理交互：随着系统变大，组件之间的交互数量快速增加，变得难以管理。通过从使用它们的程序中分离出Time.cpp这样的模块，可以最小化这些交互。

独立编译：单独的文件可以被独立编译，之后链接到一个程序中。其中的细节依赖于你的编程环境。随着程序规模变大，独立编译能节省很多时间，由于你通常每次只需要编译少数一些文件。

对于类似本书这样的小程序来说，分割程序并没有多大好处。但你最好知道这个特性，特别是它解释了我们写的第一个程序中出现的一个语句：

#include 

iostream.h是一个包含着cin和cout声明以及操作它们的函数的头文件，当编译程序时，你需要该头文件中的信息。

这些函数的实现存储在一个库中，有时候被称为"标准库"，它能自动链接到你的程序中。好处在于当你编译程序时，你不需要每次都重新编译库。大多数情况下，库不会改变，因此没有理由重新编译它。

11.11 术语表

成员函数（member function）：用于操作对象的函数，其中被操作对象作为隐式参数this传递给它。

非成员函数（nonmember function）：一类不属于任何结构体定义中的成员的函数，也称为“独立”函数。

调用(invoke)：To call a function “on” an object, in order to pass the object as an implicit parameter.

当前对象（current object）：成员函数调用的对象。在成员函数中，我们能隐式地引用当前对象，或者使用关键字this。

this：用于引用当前对象的关键字。this是一个指针，这使它不易使用，因为本书中没有涵盖指针相关内容。

接口(interface)：对函数如何使用的一个描述，包括参数的个数和类型，以及返回值的类型。

函数声明(function declaration):一条语句，声明了函数的接口，但不提供函数体。成员函数的声明出现在结构体定义中，即便函数定义在外面。

实现(implementation)：函数体或者函数的工作细节。

构造函数(constructor)：一个特殊的函数，用于初始化新创建对象的实例变量。

第12章 对象的向量

12.1 组合

到目前位置，我们已经看了几个组合的例子，所谓组合是指以各种不同的排列方式组织语言特性的能力。一个例子是将函数调用作为表达式的一部分。另一个是语句的嵌套结构：可以将if语句放到while循环中，也可以将if语句放在另一个if语句中，等等。

见识了这种模式，也学习了向量和对象，读者应该不会对对象的向量感到奇怪了。实际上，我们也可以使用包含向量（作为实例变量）的对象，可以使用向量的向量、对象的对象，诸如此类。

下面两章，我们会以纸牌对象（Card）为实例，看一下这些组合的一些例子。

12.2 纸牌对象（Card）

如果你对玩纸牌尚不熟悉，那最好现在就去拿一副，否则你会感觉这一章没什么意思。一副牌有52张，每张都有一个花色（4种花色之一）和大小（13个值之一）。按桥牌中下降的顺序排列，4种花色分别是黑桃（Spades）、红桃（ Hearts）、方块（Diamonds）和梅花（Clubs）。大小包括A、2、3、4、5、6、7、8、9、10、J、Q和K。根据不同纸牌游戏的规则，A可能比K大，也可能比2小。

如果要定义新对象表示纸牌，很明显，实例变量应该是大小和花色。不过，实例变量以什么类型定义可能就没这么明显了。一个方法是使用apstring类型，比如用字符串“Spade”表示花色，而用字符串“Queen”表示大小。其缺点是难以比较两张牌的花色和大小。

另一个可选的方法是，使用整型数给大小和花色编码。这里的编码，并不是很多人认为的加密（或者说译成密码）。在计算机科学家的心目中，编码就像是在数字序列和希望表示的事物之间定义一个映射。例如，

Spades           |→ 3
Hearts           |→ 2
Diamonds         |→ 1
Clubs            |→ 0

“ |→”是表示映射的数学符号。该映射最明显的特性是，花色按顺序映射到整型数，所以我们可以通过比较整型数来比较花色。牌大小的映射也是显而易见的，每个数字大小映射到相应的整型数，带人像的扑克牌以下面方式映射：

J       |→ 11
Q       |→ 12
K       |→ 13

使用数学符号表示映射的原因是，映射并非C++程序的一部分，而是程序设计的一部分，但是它们从来不会显式地出现在代码中。Card类型的定义如下：

struct Card
{
  int suit, rank;

  Card ();
  Card (int s, int r);
};

Card::Card () {
  suit = 0; rank = 0;
}

Card::Card (int s, int r) {
  suit = s; rank = r;
}

Card有两个构造函数，构造函数没有返回类型且与结构体同名，通过这两点可以识别它们。第一个构造函数不接受任何参数，它把实例变量初始化为无效值（梅花0）。

第二个构造函数更加有用，它有两个参数，分别是纸牌的花色和大小。

下面代码创建了一个名为threeOfClubs的对象，它表示梅花3。

Card threeOfClubs (0, 3);

第一个参数0表示花色为梅花，第二个参数自然是表示牌的大小为3。

12.3 printCard函数

创建新类型时，第一步一般是声明实例变量并编写构造函数，第二步一般是编写一个可以将对象以可读形式打印出来的函数。

对于纸牌的情况，“可读”指的是我们必须将大小和花色的内部表示映射为单词。一种自然的方法是使用apstring的向量完成该功能。你可以像创建其他类型的向量一样创建apstring的向量：

apvector<apstring> suits (4);

当然，为了使用apvector和apstring类型，必须包含它们的头文件。

为了初始化向量的元素，我们可以使用一系列赋值语句：

suits[0] = "Clubs";
suits[1] = "Diamonds";
suits[2] = "Hearts";
suits[3] = "Spades";

这个向量的状态图如下所示：

我们可以构建一个类似的向量来解码牌的大小。然后，我们就能以花色和大小为索引选择适当的元素了。最后，我们能够编写print函数来输出调用该函数的纸牌的信息：

void Card::print () const
{
  apvector<apstring> suits (4);
  suits[0] = "Clubs";
  suits[1] = "Diamonds";
  suits[2] = "Hearts";
  suits[3] = "Spades";
  apvector<apstring> ranks (14);
  ranks[1] = "1";
  ranks[2] = "2";
  ranks[3] = "3";
  ranks[4] = "4";
  ranks[5] = "5";
  ranks[6] = "6";
  ranks[7] = "7";
  ranks[8] = "8";
  ranks[9] = "9";
  ranks[10] = "10";
  ranks[11] = "Jack";
  ranks[12] = "Queen";
  ranks[13] = "King";
  cout << ranks[rank] << " of " << suits[suit] << endl;
}

表达式suits[suit]的意义是“以当前对象的实例变量suit为索引从向量suits选择适当的字符串”。

因为print是Card类的成员函数，所以它能隐式地（即不适用点记法指定对象）引用当前对象的实例变量。比如下面代码：

Card card (1, 11);
card.print ();

其输出是“Jack of Diamonds”。

你可能注意到了，我们没有使用表示牌大小的向量的第0个元素。那是因为只有1-13之间的牌大小值才是有效的。通过在向量的开头留下一个未用元素，我们得到了从2映射到“2”，3映射到“3”等这样的编码。从用户的观点看，编码是什么并不重要，因为所有的输入和输出都是用可读的形式表示的。

另一方面，如果映射易于记忆，这对程序员来说是有帮助的。

12.4 equals函数

两张牌要相等的话，必须花色和大小都相同。十分不幸，“”操作符不能用于像Card这种用户定义类型，所以我们需要自己编写一个比较两张牌的函数，即equals函数。也可以通过重写“”操作符的定义实现此功能，不过本书不做介绍了。

很明确，equals函数的返回值应该是布尔类型，用以说明两张牌是否相等。同样可以明确的是，该函数需要有两个Card类型的参数。但是我们还要做出一个选择，那就是应该把equals设计成成员函数还是独立函数？

将equals设计为成员函数，代码如下：

bool Card::equals (const Card& c2) const
{
  return (rank == c2.rank && suit == c2.suit);
}

使用这个函数时，必须通过一个对象来调用，而把另一个对象当做参数：

Card card1 (1, 11);
Card card2 (1, 11);

if (card1.equals(card2)) {
  cout << "Yup, that’s the same card." << endl;
}

在我看来，像equals这样两个参数对称的函数，这样调用看起来很奇怪。对称是指， 以“A是否等于B”或者“B是否等于Ａ”两种方式提问，其实没什么关系。既然如此，我想以非成员函数的方式重写equals函数更好：

bool equals (const Card& c1, const Card& c2)
{
  return (c1.rank == c2.rank && c1.suit == c2.suit);
}

调用这个版本的函数时，参数并肩出现，至少在我看来这样逻辑上更有意义。

if (equals (card1, card2)) {
  cout << "Yup, that’s the same card." << endl;
}

当然，这就是口味的问题了。我的观点是，不管成员函数版本还是非成员函数版本，读者都要能熟练编写，所以能根据条件选择最合适的版本。

12.5 isGreater函数

对于像int和double这样的基本类型，可以使用比较操作符比较值并判断大小。不过这些操作符（如等等）不适用于用户定义类型。就像上一节，为了实现类似==操作符的功能，我们定义了equals函数，现在我们来写一个比较函数以实现类似>操作符的作用。 后面，我们会使用这个函数对一副牌进行排序。

有些集合是完全有序的，也就是说集合中的任意两个元素都可以比较大小。例如，整型数集合和浮点数集合就是完全有序的。 而有的集合是无序的，即不存在有意义的方法来比较集合中两个元素的大小。例如，水果的集合就是无序的，这也是我们无法比较苹果和句子的原因。另一个例子，bool类型也是无序的，我们并不能说true比false大。

扑克牌集合是部分有序的，也就是说我们有时可以对牌进行比较，而有时却不能。比如，我们知道梅花3比梅花2大，因为3比2大；方块3比梅花3大，因为方块比梅花大。但是，梅花3和方块2谁大呢？一个数值更大，而另一个花色更大。

为了让卡牌称为可比较的，我们需要决定大小和花色哪个更为重要。老实说，选择完全是随意的。 为了选择，我可以说花色更重要，因为新买的牌是有序的，所有的梅花放在一起，而且都在方块的前面，诸如此类。

根据这个决策，我们就可以编写isGreater函数了。再一次，参数（两张牌）和返回类型（布尔值）是显而易见的，我们还是要在将isGreater设计为成员函数或非成员函数之间做出选择。这一次，参数不是对称的了。我们到底想知道“A是否大于B”或“B是否大于A”是很重要的。所以我认为把isGreater设计为成员函数更有意义。

bool Card::isGreater (const Card& c2) const
{
    // 首先检查花色
     if (suit > c2.suit) return true;
    if (suit < c2.suit) return false;

    // 如果花色相等，检查大小
    if (rank > c2.rank) return true;
    if (rank < c2.rank) return false;

    // 如果大小也相同，返回false
    return false;
}

调用时，根据两个可能的问题，语法也很明显：

Card card1 (2, 11);
Card card2 (1, 11);

if (card1.isGreater (card2)) {
    card1.print ();
    cout << "is greater than" << endl;
    card2.print ();
}

你几乎可以用英语读出来：”If card1 isGreater card2 …“。程序的输出是：

Jack of Hearts
is greater than
Jack of Diamonds

根据isGreater函数，牌A小于牌２。 作为联系，请修改isGreater函数，使A比K大，因为大多数纸牌游戏中都是这样的。

12.6 纸牌的向量

本章选择纸牌作为研究对象的原因是，牌堆是一个很明显的纸牌向量的应用。 这是创建一副52张牌组成的新牌堆的代码：

apvector<Card> deck (52);

这是对象的状态图:

三个点代表我不想画出的48张牌。记住，我们尚未初始化纸牌实例变量。有些环境中，它们会初始化为0，就像图中这样，而在其他环境中它们可能包含任何可能的值。

一种初始化方法是，以一个Card对象为第二个参数调用向量的构造函数：

Card aceOfSpades (3, 1);
apvector<Card> deck (52, aceOfSpades);

这段代码创建了一副由52张同样的牌组成的牌堆，就像变魔术用的特殊牌。当然，创建一副由52张不同的牌组成的牌堆才更有意义。这可以使用嵌套循环实现。

外层循环枚举了花色，从0到3。对于每种花色，内部循环枚举了牌的大小，从1到13。因为外部循环迭代4词，内部循环迭代13词，循环体总的执行次数是52次（即13乘以4）。

int i = 0;
for (int suit = 0; suit <= 3; suit++) {
  for (int rank = 1; rank <= 13; rank++) {
    deck[i].suit = suit;
    deck[i].rank = rank;
     i++;
  }
}

我们使用变量i记录牌堆中要使用的下一张牌。

注意，我们可以把数组元素选择语法（[]操作符）和对象的实例变量选择语法（点操作符）组合起来。比如表达式deck[i].suit意思是“牌堆中第i张卡的花色”。

作为练习，请把构建牌堆的代码封装为buildDeck函数，该函数不接受任何参数并返回一个完全填充的纸牌向量。

12.7 printDeck函数

使用向量时，有一个能打印向量内容的函数是很方便的。因为我们已经多次遇到过遍历向量的模式，所以下面函数读者应该很熟悉：

void printDeck (const apvector<Card>& deck) {
  for (int i = 0; i < deck.length(); i++) {
    deck[i].print ();
  }
}

到现在为止，我们能够组合向量访问语法和函数调用语法，这一点你应该不会感到奇怪。

因为牌堆的类型是apvector，每个元素都是Card类型，所以在deck[i]上调用print是合法的。

12.8 查找

我们要编写的下一个函数是find，它的作用是在纸牌向量中查找指定的牌。这个函数的用途可能不是那么明显，但是我们可以利用它来演示两种查找方法，即线性查找和二分查找。

线性查找是比较直观的一个；它包括遍历牌堆并拿每张牌和我们要找的牌进行比较。如果找到了，返回纸牌出现位置的索引；没找到则返回-1。

int find (const Card& card, const apvector<Card>& deck) {
  for (int i = 0; i < deck.length(); i++) {
    if (equals (deck[i], card)) return i;
  }
  return -1;
}

这里的循环与printDeck中的循环完全一致。实际上，这段代码是从printDeck中复制而来的，这就避免了编写和调试两次。

在循环内部，我们将牌堆中的每个元素都与指定的纸牌进行比较。一旦找到，函数就立即返回，也就是说，如果找到指定的牌，那就不需要遍历整个牌堆。如果循环结束时还没有找到，我们就可以确定牌堆中没有指定的牌，最后返回-1。

我们使用下面代码来测试该函数：

apvector<Card> deck = buildDeck ();

int index = card.find (deck[17]);
cout << "I found the card at index = " << index << endl;

这段代码的输出是：

I found the card at index = 17

12.9 二分查找

如果牌堆中的纸牌不是按顺序排列的，那就没有比线性查找更快的查找方法了。我们必须查看每张纸牌，因为除此之外我们无法确定要找的纸牌是不是在其中。

但是查词典时，我们并不是从头到尾、一个词一个词的查。因为单词是以字母顺序排列的，所以我们可以使用类似于二分查找的算法：

1. 从中间某个位置开始。
2. 在这一页上选择一个单词，并用这个单词和我们要查找的单词比较。
3. 如果这就是我们要找的单词，结束。
4. 如果我们要找的单词在这一页上的单词之后，翻到后面某页并回到第2步。
5. 如果我们要找的单词在这一页上的单词之前，翻到词典前面某页并回到第2步。

如果遇到了这种情况，某页上有两个相邻的单词，而要找的单词应该在它们之间，这时即可确定词典中没要我们要查的单词。唯一的例外就是单词印错地方了，但这就与单词按字母顺序排列的假设冲突了。

在牌堆这个例子中，如果知道纸牌是有序摆放的，我们就能写一个更快的find函数。编写二分查找最好的方法是利用递归函数，因为二分自然而然是递归的。

窍门是编写findBisect函数，它以两个索引值low和high为参数，用以确定要查找的向量的一段（包括low和high指定的元素）。

1. 要在向量中查找，选择low和high之间的一个索引，我们称之为mid。将mid指定的纸牌与我们要查找的牌相比。
2. 如果找到，结束。
3. 如果mid处的纸牌比要找的牌大，继续在low和mid-1确定的区间中查找。
4. 如果mid处的纸牌比要找的牌小，继续在mid+1和high确定的区间中查找。

可以怀疑第3步和第4步看起来像递归调用。我们将其转化为C++代码，看起来是这个样子的：

int findBisect (const Card& card, const apvector<Card>& deck,
                        int low, int high) {
  int mid = (high + low) / 2;

  // 如果找到了纸牌，返回其index
  if (equals (deck[mid], card)) return mid;

  // 否则，将纸牌与中间的纸牌比较
  if (deck[mid].isGreater (card)) {
    // 查找纸牌的前一半
    return findBisect (card, deck, low, mid-1);
  } else {
    // 查找纸牌的后一半
    return findBisect (card, deck, mid+1, high);
  }
}

虽然这段代码已经包含了二分查找的核心，但还是缺点什么。按照当前代码，如果要找的纸牌不再牌堆中，它会一直递归下去。我们需要找到一种方法来检查这一条件并做出适当的处理（通过返回-1）。

识别出目标纸牌不在牌堆中最简单的方法是，牌堆中没有纸牌，也就是high小于low的情况。当然，牌堆中仍然有牌，我的意思是由low和high指定的段中没有纸牌。

添加了high

int findBisect (const Card& card, const apvector<Card>& deck,
                        int low, int high) {

  cout << low << ", " << high << endl;

  if (high < low) return -1;

  int mid = (high + low) / 2;

  if (equals (deck[mid], card)) return mid;

  if (deck[mid].isGreater (card)) {
  return findBisect (card, deck, low, mid-1);
  } else {
    return findBisect (card, deck, mid+1, high);
  }
}

我在开头添加了一行输出语句，这样我们能查看递归调用序列并说服我们递归会走到基本条件。尝试下面代码

cout << findBisect (deck, deck[23], 0, 51));

其输出如下：

0, 51
0, 24
13, 24
19, 24
22, 24
I found the card at index = 23

然后，我编造了1张不在牌堆中的牌——方块15，然后试一下查找它，输出如下：

0, 51
0, 24
13, 24
13, 17
13, 14
13, 12
I found the card at index = -1

这些测试并不能证明程序的正确性，其实再多的数据也无法证明程序是正确的。但是看几个例子并检验代码，也许可以说服你自己。

递归调用的次数相当少，通常是6或7次。也就是说equals函数和isGreater函数只需要调用6或7次，而线性查找最多要调用52次。一般而言，二分查找比线性查找快的多，尤其是向量中元素数目很多时，效果更为明显。

递归程序中两个常见错误，一个是忘记了包含基本条件，另一个是递归调用永远取不到基本条件。每个错误都会导致无穷递归，这种情况下C++最终会出现运行时错误。

12.10 牌堆与子牌堆

请看函数findBisect的接口：

int findBisect (const Card& card, const apvector<Card>& deck,int low, int high) 

把三个参数deck，low和high看作指定一个子牌堆的单一参数是可以说得通的。

这种事情很常见，有时我把它当作抽象参数。所谓”抽象“，我指的是在更高层次上描述函数，并非程序代码的字面意思。

例如，当以向量以及用以限界的low和high为参数调用函数时，其实根本没办法限制函数中访问界限之外的元素。所以我们并没有像字面上说的那样传递了子牌堆，但是只要被调函数按规矩办事， 抽象的将参数当做子牌堆是有意义的。

还有一个例子，你可能已经注意到了，在9.3节，我提到“空”数据结构时也用到了这种抽象。“空”上的引号就是为了提醒读者，这并非是字面意义上真正的空。所有的变量自始至终都是有值的。创建变量之时，它们会有默认值。所以没有空对象这样的东西。

但是，如果程序确保变量的当前值在写之前从未被读过，则当前值是无意义的值。抽象地讲，把这种变量当做”空“值是说得通的。

这种思考方式——即程序带上了超出编码字面意思之外的意义——是像计算机科学家一样思考问题的一个重要部分。有时，”抽象“这个词用的太多、太杂，可能难以解释。尽管如此，抽象仍然是计算机科学（以及很多其他领域）的一个中心思想。

“抽象”的一个更一般的定义是“为了抓住重要行为且抑制不必要的细节，使用简单的描述建模复杂系统的过程”。

12.11 术语表

编码（encode） ：通过在两个集合间构造映射，使一个集合中的值可以用另一个集合中的值表示。.

抽象参数（abstract parameter）： 看以看作一个单一参数的几个参数的集合。

第13章 基于向量的对象

13.1 枚举类型***

上一章我们谈到了从真实世界的值（如扑克牌中的大小和花色）到程序世界内部表示（如整数或字符串）的映射。虽然我们实现了牌面大小和整型数、花色和整型数之间的映射，但必须指出，映射本身并没有成为程序的一部分。

实际上，C++提供了一种称为“枚举类型”的特性使以下两点成为可能，一是将映射作为程序的一部分，一是定义了组成映射的值的集合。比如，牌的花色（Suit）和大小（Rank）可以以枚举的形式定义：

enum Suit { CLUBS, DIAMONDS, HEARTS, SPADES };
enum Rank { ACE=1, TWO, THREE, FOUR, FIVE, SIX, SEVEN, EIGHT, NINE,
TEN, JACK, QUEEN, KING };

默认情况下，枚举类型中的第一个值映射为0，第二个映射为1，以此类推。如在Suit类型中，CLUBS（梅花）使用整型数0表示， DIAMONDS（方块）使用1表示，等等。

Rank的定义中将ACE指定为1，覆盖了默认的映射值。其他值以自然的方式递推。

定义了这些类型之后，我们就可以在任何地方使用它们。比如，实例变量rank和suit可以分别用类型Rank和Suit来声明：

struct Card
{
  Rank rank;
  Suit suit;
  Card (Suit s, Rank r);
};

构造函数的参数类型也相应改变了。现在，我们可以以枚举类型的值为参数创建Card对象：

Card card (DIAMONDS, JACK);

一般约定，枚举类型中值的名字全部用大写字母表示。上面代码要比下面使用整型数的方式清晰地多：

Card card (1, 11);

枚举类型中的值是用整型数表示的，所以可用作向量的下标。因此原来的print函数不加修改即可工作。不过buildDeck还是要做些修改，如下：

int index = 0;
for (Suit suit = CLUBS; suit <= SPADES; suit = Suit(suit+1)) {
  for (Rank rank = ACE; rank <= KING; rank = Rank(rank+1)) {
    deck[index].suit = suit;
    deck[index].rank = rank;
    index++;
  }
}

从某种程度上说，枚举类型的使用会让代码的可读性更好，不过同时也带来了一点混乱。严格地讲，不允许在枚举类型上执行数学运算，如suit++是不合法的。 而另一方面，在表达式suit+1中，C++自动将枚举类型转换为整型数，然后我们可以将结果强制转换为枚举类型：

suit = Suit(suit+1);
rank = Rank(rank+1);

当然，还有一种更好的处理方法，那就是为枚举类型重载++操作符，但这已经超出本书的范围了。

13.2 switch语句

谈到枚举类型就不得不提switch语句，因为它们经常一起出现。switch语句是表示一组条件选择的另一种方式，而且语法上更漂亮，往往执行上也更有效率。switch语句看起来是这个样子的：

switch (symbol) {
case '+':
  perform_addition ();
  break;
case '*':
  perform_multiplication ();
  break;
default:
  cout << "I only know how to perform addition and multiplication" << endl;
  break;
}

switch语句与下面一组条件语句等价：

if (symbol == '+') {
  perform_addition ();
} else if (symbol == '*') {
  perform_multiplication ();
} else {
  cout << "I only know how to perform addition and multiplication" << endl;
}

switch语句每个分支中的break是必须的，否则执行流会贯穿到下一个case条件。如果没有break语句，symbol为 ‘+’时，程序会先执行加法，然后执行乘法，最后打印错误信息。这个特性偶尔也用得到，不过大多数情况下，当程序员忘记break时，这是错误之源。

switch语句可以使用整型数、字符型和枚举类型。比如，可以这样把Suit变量值转换为相应的字符串：

switch (suit) {
case CLUBS: return "Clubs";
case DIAMONDS: return "Diamonds";
case HEARTS: return "Hearts";
case SPADES: return "Spades";
default: return "Not a valid suit";
}

这种情况并不需要break语句，因为return会使函数的执行流程返回到调用处，不会贯穿到下一个case条件。

一般，在每个switch语句中都包含一个default条件——用以处理错误和意外值——是个好的编程风格。

13.3 牌堆

上一章我们用到了对象的向量，我也提到可以把向量用作对象的实例变量。本章我们就来创建包含Card向量的Deck对象。

Deck结构可以这样定义：

struct Deck 
{
  apvector<Card> cards;
  Deck (int n);
};

Deck::Deck (int size)
{
  apvector<Card> temp (size);
  cards = temp;
}

实例变量名cards可以让我们将Deck对象和它包含的Card向量区分开。

目前Deck定义中只有一个构造函数。该构造函数中先创建了局部变量temp，temp以size为参数调用apvector的构造函数完成初始化。 然后将向量从temp复制到实例变量cards中。

现在，我们可以用下面语句创建一个扑克牌的牌堆：

Deck deck (52); 

这是Deck对象的状态图：

deck对象包含实例变量cards，其中cards是Card对象的向量。我们可以通过组合对象访问语法和数组元素选择语法来访问deck对象中的cards（也就是要获取牌堆中牌的信息）。比如，表达式deck.cards[i]得到牌堆deck的第i张牌，deck.cards[i].suit得到这张牌的花色。下面的循环语句说明如何遍历牌堆并输出其中的每章牌：

for (int i = 0; i<52; i++) {
  deck.cards[i].print();
}

13.4 另一个构造函数

有了Deck对象之后，我们有必要初始化其中的Card对象。上一章的buildDeck函数稍作修改就可使用，但是更自然的方法是为Deck类再添加一个构造函数，代码如下：

Deck::Deck ()
{
  apvector<Card> temp (52);
  cards = temp;
  int i = 0;
  for (Suit suit = CLUBS; suit <= SPADES; suit = Suit(suit+1)) {
    for (Rank rank = ACE; rank <= KING; rank = Rank(rank+1)) {
      cards[i].suit = suit;
      cards[i].rank = rank;
      i++;
    }
  }
}

可以看到，除了语法变成了构造函数，它与buildDeck函数非常相似。现在，用简单的声明语句

 Deck deck;

就能创建一个标准的52章牌的牌堆了。

13.5 Deck成员函数

有了Deck对象之后，把所有从属于Deck的函数放入其结构定义中也是情理之中的事了。看一下到目前为止我们定义的函数，很明显12.7节的printDeck函数可以作为候选加进来。下面将printDeck重写为成员函数：

void Deck::print() const {
  for (int i = 0; i < cards.length(); i++) {
    cards[i].print ();
  } 
}

通常，引用当前对象不需要使用点记号。

其他几个函数，至于是否应将它们变为Card或Deck的成员函数，还是作为以Card或Deck变量为参数的非成员函数，并非显而易见的。比如上一章以一个Card变量和一个Deck变量为参数的find函数，将它变为Card或Deck类型的成员函数都是合理的。作为练习，请重写find函数，其参数为Card类型，使之成为Deck的成员函数。

将find改写为Card的成员函数需要一些小技巧，这是我写的版本：

int Card::find (const Deck& deck) const {
  for (int i = 0; i < deck.cards.length(); i++) {
    if (equals (deck.cards[i], *this)) return i;
  }
  return -1;
}

一个技巧是，必须使用this关键字来引用调用find函数的对象；再就是在C++中定义相互引用的结构也需要一点技巧，因为编译器正在读取第一个结构定义时还不知道第二个结构的定义。

一种解决方案是，在Card定义之前先声明Deck，以后再给出Deck的定义。

// 声明Deck结构，这里不定义declare that Deck is a structure, without defining it
struct Deck;

// 这样我们就可以在Card的定义中引用Deck
struct Card
{
  int suit, rank;
  Card ();
  Card (int s, int r);
  void print () const;
  bool isGreater (const Card& c2) const;
  int find (const Deck& deck) const;
};

// 后面给出Deck的定义
struct Deck {
  apvector<Card> cards;

  Deck ();
  Deck (int n);
  void print () const;
  int find (const Card& card) c

13.6 洗牌

大多数纸牌游戏都需要洗牌，也就是让纸牌随机排列。在第10.5节，我们看到了怎样生成随机数，但怎样利用随机数实现洗牌功能却并非显然意见的。

一种可行的方案是，模拟人洗牌的方法，将牌分为两堆，然后通过在每个牌堆中轮流选择的方式实现原牌堆的重新组织。因为一般而言，人并不能做到完美地洗牌，而程序经过大约7次迭代之后，牌堆中纸牌的顺序已经相当随机了。但是计算机程序每次在做完美洗牌的时候有一个令人讨厌的属性——它并非真正随机的。实际上，经过8次完美洗牌之后，你会发现牌堆又回到原来的排列了。关于这一结论的讨论，请参考http://www.wiskit.com/marilyn/craig.html，或者以“perfect shuffle”为关键词通过搜索引擎查询相关信息。

还有一个更好的洗牌算法：遍历牌堆，每次选择一张纸牌，每次迭代时选择两张纸牌并交换其位置。

下面代码是该算法工作原理的大体轮廓。为了大概说出程序的意思，我混用了C++语句和自然语言句子，这有时也称为伪代码：

for (int i=0; i<cards.length(); i++) {
// 在i和cards.length()之间选择一个随机数
// 将第i张牌和随机选择的纸牌交换
}

伪代码的优点是能清晰地表达出你需要的函数。在这个例子中，我们需要像randomInt这样的函数用于在参数low和high之间选择一个随机数，也需要swapCards这样的函数用于交换两个索引值指定的位置的纸牌。

看一下第10.5节，你就应该能想出怎么编写randomInt函数了，尽管还是要小心处理生成的可能在区间之外的索引值。

你也可以自己想出swapCards函数。这些函数的剩余实现就作为作业留给读者。

13.7 排序

既然牌堆中的纸牌顺序已经乱了，我们还是需要一种让纸牌重新有序的方法。讽刺的是，有一个排序算法与洗牌算法很相似。

再一次，我们遍历牌堆，而且在每个位置都选择另一张纸牌并交换。唯一的区别是，这次我们不是随机的选择另一张牌，而是选择剩余牌堆中最小的纸牌。

“剩余牌堆中”指的是以i或i右侧的值为索引的纸牌。

for (int i=0; i<cards.length(); i++) {
  // 在位置i及其右侧找到最小的纸牌
  // 将第i张纸牌与最小的纸牌交换
}

此外，伪代码有助于辅助函数的设计。这种情况下，我们又能使用findLowestCard了，它接收纸牌向量和我们要开始查找的位置的索引值。

使用伪代码指出需要什么辅助函数的过程称为自上而下的设计，它不同于我们在10.8节讨论的下下而上的设计。

我们再次把实现留给读者。

13.8 子牌堆

我们应该如何表示一手牌或者一副牌的某个子集呢？很容易的选择就是创建一个少于52张纸牌的Deck对象。

我们可能需要一个subdeck函数，它以一个纸牌向量和索引的区间为参数，返回值是一个新的向量，其中包括了牌堆中指定的子集：

Deck Deck::subdeck (int low, int high) const {
  Deck sub (high-low+1);

  for (int i = 0; i<sub.cards.length(); i++) {
    sub.cards[i] = cards[low+i];
  }
  return sub;
}

我们使用Deck的构造函数创建局部变量subdeck（译者注：参考代码，这里应该是sub，下同），其参数为牌堆大小，这里没有对其中的纸牌进行初始化，其初始化是通过复制原始牌堆中的纸牌完成的。

subdeck的长度是high-low+1，因为区间下界和上界的牌都包括在其中。这个计算虽然简短但还是容易让人迷惑，进而导致“差一错误”。要避免这种错误，最好通过画图来辅助理解。

作为练习，请编写另一个版本的findBisect函数，它以一个子牌堆为参数，而不是以一个牌堆和索引区间为参数。哪个版本更容易出错？你认为哪个版本会更高效？

13.9 洗牌与发牌

在第13.6节我们编写了一个洗牌算法的伪代码。假设shuffleDeck函数实现洗牌功能，其参数为一个牌堆，我们就可以这样创建牌堆并洗牌：

Deck deck;       // 创建一个标准的52张牌的牌堆
deck.shuffle (); // 洗牌

然后，使用subdeck函数来分几手牌：

Deck hand1 = deck.subdeck (0, 4);
Deck hand2 = deck.subdeck (5, 9);
Deck pack = deck.subdeck (10, 51);

这段代码将前5张纸牌分到一个牌堆中，接下来的5张分到一个牌堆中，剩下的作为一个牌堆。

在考虑发牌的时候，你是不是认为我们应该像实际游戏中常用的那样轮流着每次给每个玩家发一张牌？我也这样想过，但我意识到，对计算机程序而言这是不必要的。轮流发牌有两个目的，一是为了降低洗牌缺陷带来的问题，再就是使发牌者更难作弊。而这些对计算机而言都不是问题。

这个例子是个有益的提醒，那就是要小心工程隐喻的一点危险之处：有时我们给计算机施加了不必要的限制，或者期望计算机缺乏的功能，就是因为我们轻率地将隐喻扩展到了崩溃的边缘。一定要小心误导性的类比。

13.10 归并排序

在第13.7节，我们见到一个简单的排序算法，结果它不够高效。要排序n个项目，该算法必须遍历向量n次，而且每次遍历花的时间也是与n成比例的。因此，总时间与n2（这里表示n平方，下同）成比例。

本节我们会简单介绍一个更高效的算法——归并排序。要对n个项目进行排序，归并排序消耗的时间与nlogn成比例。这个数字看起来可能不会给人留下深刻印象，但是随着n增大之后，n2和nlogn的差距是巨大的。你可以自己找一些n值来试试看。

归并排序背后的基本思路是：如果有两个子牌堆，每个都是已经排序好的，那将它们合并成一个有序的牌堆是很容易的（而且很快速）：

1. 形成两个子牌堆，每个牌堆大约10张纸牌，分别排序，正面朝上时最小的牌在最上面。让这两个牌堆都正面朝你。
2. 比较每个牌堆最上面的纸牌，选择小的并将它翻过来放到归并后的牌堆中。
3. 重复步骤2直到其中一个牌堆为空时为止。然后将剩下的牌加到归并后的牌堆中。

我们得到的结果就是一个有序的牌堆。该算法的伪代码看起来是这个样子的：

Deck merge (const Deck& d1, const Deck& d2) {
  // 创建一个足够保存所有牌的新牌堆
  Deck result (d1.cards.length() + d2.cards.length());

  // 使用索引i记录在当前处理的第一个牌堆中的位置
  // 使用索引j记录第二个牌堆中的位置
  int i = 0;
  int j = 0;

  // 索引k用于遍历保存结果的牌堆
  for (int k = 0; k<result.cards.length(); k++) {

    // 如果d1为空，选择d2；如果d2为空，则选择d1
    // 否则，比较两张纸牌
    // 将选择的纸牌加入到结果牌堆中
  }
  return result;
}

因为两个参数是对称的，所以我选择将merge设计为非成员函数。要测试merge函数，最好的方法莫过于创建一副牌并洗牌，使用subdeck函数将牌分为两小堆，然后使用上一章的sort函数将两个子牌堆排序。之后，你就可以把这两个子牌堆传给merge函数来验证下它能否正常工作了。

如果你能让这一想法称为可行的，请尝试一下mergeSort的一个简单实现：

Deck Deck::mergeSort () const {
  // 找到牌堆的中点
  // 将牌堆划分为两个子牌堆
  // 使用sort函数对子牌堆进行排序
  // 合并两个子牌堆并返回结果
}

注意，当前对象声明为const，因为mergeSort不需要修改它。 相反，函数中创建了一个新的Deck对象并返回。

如果你能让这一版本正常工作，真正有趣的事情要开始了！mergesort的神奇之处在于，它是递归的。在对子牌堆进行排序时，为什么要调用老版本的较慢的sort函数？为什么不调用我们正在编写的这个出色的、新的mergeSort函数？

这不仅是一个好想法，为了取得我承诺的性能优势，这也是必要的。尽管为了让它能正常工作，你必须添加一个基本条件，这样才不会无限递归下去。一个简单的基本条件是，子牌堆中有没有牌或者只有1张牌。如果mergesort接受的是这样小的子牌堆，不需要修改就可以直接返回，因为这样的牌堆已经是有序的。

递归版本的mergesort看起来应该是这个样子的：

Deck Deck::mergeSort (Deck deck) const {
  // 如果牌堆中只有0或1张纸牌，直接返回该牌堆

  // 找到牌堆中的中点
  // 将牌堆划分为两个子牌堆
  // 使用mergeSort对子牌堆进行排序
  // 将两个子牌堆合并到一起并返回该结果
}

像往常一样，思考递归程序有两种方法：一个是考虑清楚完整的执行流程，另一个就是通过“思路跳跃”的方式。我有意的通过构造这个例子鼓励你使用“思路跳跃”来思考问题。

当使用sort来对子牌堆进行排序的时候，你并没有感觉到不得不跟踪执行流程，对不对？ 这正是因为你假设了sort函数能正常工作，因为你已经调试过这个函数。好了，要让mergeSort成为递归的，所有你需要做的就是用这个排序函数替换掉老的。没有理由读不同的程序。

实际上你必须考虑正确的基本条件，还要确认最终能到达基本条件，但除此之外，写一个递归版本应该是没什么问题的。祝你好运！

13.11 术语表

伪代码（pseudocode）： 一种通过混合使用自然语言和C++来写出程序草图的程序设计方式。

辅助函数（helper function）： 一般指本身并不是非常有用，但可以让其他函数更有用的小函数。

自下而上的设计（bottom-up design）： 一种程序开发方法，使用伪代码写出大问题解决方案的大体轮廓，并且设计出辅助函数的接口。

归并排序（mergesort）： 对一组数据进行排序的算法。归并排序比上一章的简单排序算法要快，对于大数据集尤为明显。

第14章 类与不变式

14.1 私有数据和私有类

本书之前提到了“封装”的概念，即指将一系列指令放在一个函数体内部的处理过程。而这样的做法则是为了将函数的接口与它的实现分离（函数接口指如何使用这个函数，函数实现则指如何去实现这个函数及实现具体做了些什么）。上面提到这种封装可以命名为“功能封装”，用以区分本章将要介绍的“数据封装”。数据封装是基于这样的理念提出的：每一个结构的定义应当包括应用于本结构的函数集以及阻止对内部的无限制访问。数据封装的应用之一在于隐藏用户或程序员不必了解的那些实现层次的细节。比如对于一张“扑克”的花色和点数可以有很多种表达方式，可以用两个整数，两个字符串或者两个枚举类型。而实现这个“扑克”类的作者需要知道如何实现它，使用这个“扑克”的其他人就不应该知道它的内部结构了。 另外一个例子，我们之前使用apstring和apvector对象却未曾讨论过他们的实现方式。实现方式可以有很多种，但作为使用这些库的“客户”则不必知晓。在C++中确保数据封装的通常办法是通过禁止客户程序访问对象的变量来实现的。在结构定义时使用关键字private进行保护。比如，我们有如下的“扑克”定义。

struct Card
{
private:
        int suit, rank; //suit为花色，rank牌大小
public:
       Card ();
       Card (int s, int r);

       int getRank () const { return rank; }
       int getSuit () const { return suit; }
       void setRank (int r) { rank = r; }
       void setSuit (int s) { suit = s; }
};

该定义中分为两个部分：私有部分和公共部分。函数是公共的，这就意味着他们可以被用户程序调用。变量是私有的，于是他们就只能被“扑克”的成员函数进行读写。但通过访问函数（以get和set开头的函数）可以实现用户程序对私有变量的读写。从另一方面来看，通过访问函数就可以很容易的控制哪个操作用户可以实施于哪个变量上。比如，让所有的牌在创建之后是只读是一个好主意。为了实现这个目的，我们需要做的只需移除所有的set函数。使用访问函数的另外一个优点则是我们可以改变扑克的内部表达形式而不必更改用户的程序。

14.2 什么是类？

在大多数面向对象的编程语言中，类即为包含一系列函数的用户自定义类型。正如我们看到的这样，C++中的结构体就符合这样的定义。但C++中有另外的结构也符合这一定义；说起来有点令人迷惑，这一结构就是类（class）。 在C++中，类就是变量默认为私有的结构体。举例来说，我可以把“纸牌”结构体定义改成这样。

class Card
{
        int suit, rank;

public:
        Card ();
        Card (int s, int r);

        int getRank () const { return rank; }
        int getSuit () const { return suit; }
        int setRank (int r) { rank = r; }
        int setSuit (int s) { suit = s; }
};

我把struct改为class并去掉了private:这样的标号。除了这两处，两个定义完全一致。事实上，任何可以写成struct的都可以写成class，只是添加删除标号而已。除了风格方面的原因，不必在二者之中进行过分取舍，不过大多数C++程序员使用class。另外，通常把所有C++中自定义类型叫做“类（class）”，无论他们是被定义为struct或class。

14.3 复数

本章后面的部分讲述复数这样一个例子。复数在数学和工程领域很有用途，许多计算用到了复数。一个复数是实部和虚部之和，记作x+yi，x为实部，y为虚部，i是-1的平方根。以下为类Complex的定义：

class Complex
{
     double real, imag;

public:
     Complex () { }
     Complex (double r, double i) { real = r; imag = i; }
};

在类的定义中，实部和虚部是私有的，构造函数是公有的，故加上public标号。一般使用这样两个构造函数：一个没有参数也不做什么工作的构造函数，另一个有两个参数来用来初始化变量。到现在为止，还看不到将变量私有化的明显优点。让我们把程序复杂一点，就能看到了。对于复数，通常会有另外一种表达方式叫做基于极坐标系的极坐标表示。跟用复数域上的点的特定位置表示实部虚部不同，极坐标系中用离开原点的距离（或模）和偏离原点的方向（或角度）来表示。下图表示两个坐标系系统。

在极坐标系中，复数记作reiθ ，其中r是模（半径），θ是用弧度表示的角度。幸运的是，很容易从两个坐标系中进行转换。从笛卡尔到极坐标系：r = x2 + y2θ = arctan(y/x)从极坐标系到笛卡尔坐标系：x = r cos θ y = r sin θ那么我们应该使用哪一种表达方式呢？因为有些操作在笛卡尔坐标系中简单些，如加法；而另一些操作在极坐标系中简单些，如乘法。所以一个办法是我们写一个使用两种表达方式的类，让他们根据需要可以自动转换。

class Complex
{
        double real, imag;
        double mag, theta;
        bool cartesian, polar;
public:
        Complex () { cartesian = false; polar = false; }
        Complex (double r, double i)
        {
                real = r;  imag = i;
                cartesian = true; polar = false;
        }
};

在这个类中有6个变量，这就意味着这样会比之前的任何一种占用的空间都要多。不过我们很快就会看到这样做是很有用的。其中四个变量可以根据名字判断他们的意思，分别是一个复数的实部，虚部，角度，半径。另外两个变量cartesian和polar则是表示对应坐标系的值是否有效的标志。举例来说，啥都不做的这个构造函数将两个标志量设置为false表明该对象无论哪种表达方式，都还不是有效的复数。第二个构造函数使用参数来初始化实部和虚部，但不会计算模或角度。并会把极坐标的标志位置为false来警告其他函数不应当访问模或角度值，直到他们被设置为正确的值。现在应该清楚为何将变量置为私有了吧。如果一个客户程序被允许不受限制的访问，读取了未初始化的值就很容易导致出错。在下一部分，我们将添加一些访问函数来避免这种错误。

14.4 访问函数（Accessor functions）

按照惯例，访问函数以这样的方式命名：get + 变量的名字。返回值类型通常是对应的变量的类型。 在这个例子中，访问函数可以让我们在得到某个值前确保该值是有效的。函数getReal如下：

double Complex::getReal ()
{
    if (cartesian == false) calculateCartesian ();
    return real;
}

如果笛卡尔坐标系的标志位为真，那么real变量中包含着有效的数据，我们在getReal中将其返回即可。为假，我们就需要调用calculateCartesian从极坐标系转化到笛卡尔坐标系。

 void Complex::calculateCartesian ()
{
        real = mag * cos (theta);
        imag = mag * sin (theta);
        cartesian = true;
}

假设极坐标系的值是有效的，我们就可以使用前一部分提到的公式来转换到笛卡尔坐标系。然后我们设置笛卡尔坐标系的标志位，表明现在的real和imag的值已有效。作为练习，写一个对应于calculateCartesian的一个calculatePolar和对应的getMag 及 getTheta方法。关于访问函数一个特殊的地方在于他们不是常量，因为调用访问函数可能需要更改对应的变量。

14.5 输出

我们定义了一个新的类通常会想将其对象以可读的形式输出出来。对于复数对象，我们使用这样两个函数：

void Complex::printCartesian ()
{
        cout << getReal() << " + " << getImag() << "i" << endl;
}

void Complex::printPolar ()
{
        cout << getMag() << " e^ " << getTheta() << "i" << endl;
}

在此我们不必担心不同象限的表达方式就可以输出任何复数对象。因为两个输出函数使用了访问函数，程序会自动计算需要的值。以下代码使用第二个构造函数来创建一个复数对象，他只是是以笛卡尔坐标系的形式。 当我们调用到printCartesian时，不必做任何转换即可直接访问real 和imag。Complex c1 (2.0, 3.0);c1.printCartesian();c1.printPolar();当我们调用到printPolar,时，后者会调用getMag，程序会进行极坐标系转换并将结果保存到变量中。这种转换只需一次。当printPolar调用getTheta时，就会看到极坐标系的数值已经是有效的了，直接返回即可。以上代码的输出为：2 + 3i3.60555 e^ 0.982794i我们定义了一个新的类通常会想将其对象以可读的形式输出出来。对于复数对象，我们使用这样两个函数：

void Complex::printCartesian ()
{
        cout << getReal() << " + " << getImag() << "i" << endl;
}

void Complex::printPolar ()
{
        cout << getMag() << " e^ " << getTheta() << "i" << endl;
}

在此我们不必担心不同象限的表达方式就可以输出任何复数对象。因为两个输出函数使用了访问函数，程序会自动计算需要的值。以下代码使用第二个构造函数来创建一个复数对象，他只是是以笛卡尔坐标系的形式。 当我们调用到printCartesian时，不必做任何转换即可直接访问real 和imag。Complex c1 (2.0, 3.0);c1.printCartesian();c1.printPolar();当我们调用到printPolar,时，后者会调用getMag，程序会进行极坐标系转换并将结果保存到变量中。这种转换只需一次。当printPolar调用getTheta时，就会看到极坐标系的数值已经是有效的了，直接返回即可。以上代码的输出为：2 + 3i3.60555 e^ 0.982794i

14.6 复数相关函数（一）

对复数做加法是一个很常见的操作。复数在笛卡尔坐标系上的加法是很简单的，只需对实部虚部分别相加即可。如果在极坐标系中进行加法，最简单的方式则是将复数转换到笛卡尔坐标系中再进行相加。于是，使用访问函数就可以很容易的做到：

Complex add (Complex& a, Complex& b)
{
        double real = a.getReal() + b.getReal();
        double imag = a.getImag() + b.getImag();
        Complex sum (real, imag);
        return sum;
}

注意add函数的参数不是常量，因为我们在使用访问函数时可能更改他们。调用add函数，需要传递两个参数，如：Complex c1 (2.0, 3.0);Complex c2 (3.0, 4.0);

Complex sum = add (c1, c2);sum.printCartesian();该程序的输出结果为：5 + 7i

14.7 复数相关函数（二）

另外一个我们需要的操作则是乘法。不像加法那样，乘法在极坐标系中容易，在笛卡尔坐标系中麻烦些（是相对有点麻烦而已）。在极坐标系，我们**只需将模相乘，角度相加。**像往常那样，我们使用访问函数来实现而不必关心对象的表现形式。

Complex mult (Complex& a, Complex& b)
{
        double mag = a.getMag() * b.getMag()
        double theta = a.getTheta() + b.getTheta();
        Complex product;
        product.setPolar (mag, theta);
        return product;
}

这儿我们遇到一个小问题，即我们没有一个构造函数来接收极坐标系的值。添加这样的一个构造函数也可以，但是要记得只有在参数不同时才能重载一个函数（包括构造函数）。在这个例子中，我们要添加的构造函数仍然是接收两个浮点型的参数，所以没法重载。另外一个办法是提供一个访问函数来设置变量的值，为使操作正常进行，我们需要确保当mag与theta的值被设定时，极坐标的标志位也要设置为真，同时还要确保笛卡尔坐标系的标志位设置为假。这是因为，如果我们手动设置了极坐标的值，笛卡尔坐标系的值就会失效。

void Complex::setPolar (double m, double t)
{
        mag = m;     theta = t;
        cartesian = false; polar = true;
}

作为练习，请写出对应的函数setCartesian。为测试mult函数，我们可以这样做：Complex c1 (2.0, 3.0);Complex c2 (3.0, 4.0);

Complex product = mult (c1, c2);product.printCartesian(); 该程序的输出结果为：-6 + 17i在这个输出的背后进行了很多转换。当我们调用mult时，两个参数为被转换为极坐标系的表示形式。结果也是极坐标形式，当我们调用printCartesian时，就会再转换回笛卡尔坐标系的形式。没错，我们就这样得到了正确结果，很奇妙吧。

14.8 不变式

对于一个复数对象，有些条件我们期望是真的。举例来说，如果笛卡尔坐标系的标志量被设置了，那么我们就期望real和imag的值是有效的，类似地，如果极坐标系的标志量被设置了，我们期望mag和theta也是有效的。最后，如果两个标志位都设置了的话，我们希望四个值是一致的，即他们应该是以不同的表示方式表示相同的一个复数。这样的条件即为不变式，由于很显而易见的原因他们是不变的——他们总是应该为真。编写几乎没有bug的高质量代码就是要指出你的类中那些是不变式，并让改变他们成为不可能。数据封装的好处之一就是帮助保证不变式。第一部是通过将变量变为私有从而阻止不受约束的访问。然后更改对象的唯一办法就是通过访问函数和更改器了。如果我们检查所所有的访问函数和更改器并发现他们都能保证不变式不变，那么我们就可以证明一个不变式是不会被篡改的了。在Complex 类中，我们列出对变量进行赋值的函数：第二个构造函数calculateCartesiancalculatePolarsetCartesiansetPolar在每一个函数中，很明显他们能保持上面提到的不变性。这里我们需要小心一些。注意到我说的是“保持”不变性。这就意味着，如果这个不变式为真，那么当这个函数被调用后仍然为真。这样的定义允许了两处漏洞。首先在函数执行过程中可能有不变式为假的情况，这是没关系的，有些时候是不可避免的。只要不变式在函数执行之后恢复即可。另外一处漏洞是如果在函数执行开始时不变式为真我们只需保持该不变性即可。如果开始执行时部位真，所有都是徒劳了。如果不变式在某处被更改了，我们能做的一般来说就是检测到出错，打印错误信息，然后退出。

14.9 先决条件

通常当你写函数时会对接收的参数做了隐含的假设。如果这些假设成立，程序没有问题；如果假设不成立，你的程序可能就会崩溃了。为了让你的程序更为健壮，将你的假设明确，以程序文档的方式写下来或写代码来进行检查。比如我们观察calculateCartesian方法。是否存在对当前对象进行了假设呢？没错，我们假设极坐标系的标志量已经设置了并且mag和theta的值是有效的。如果假设不成立，那么这个函数的结果无意义。一种做法是对函数添加注释说明先决条件以警告他人。

void Complex::calculateCartesian ()
// 先决条件：当前对象包含有效的极坐标值，其极坐标标志量已设定。
// 后置条件：当前对象包含有效的笛卡尔坐标系和极坐标系的值，两个标志量皆已设置。
{
        real = mag * cos (theta);
        imag = mag * sin (theta);
        cartesian = true;
}

同时，我添加了后置条件，即我们认为函数执行完毕后为真的事情。这些注释对于阅读你代码的人很有用，但更好的办法是通过代码来检查先决条件，并输出合适的错误信息：

void Complex::calculateCartesian ()
{
        if (polar == false) {
                cout << "calculateCartesian failed because the polar representation is invalid"  << endl;
                exit (1);
        }
        real = mag * cos (theta);
        imag = mag * sin (theta);
        cartesian = true;
}

exit函数会使程序很快的退出执行。返回值是一个错误码以告诉系统（或该程序执行者）某些错误发生。这种错误检测方式很是常见，于是C++提供了一个内置函数来检查先决条件并打印错误信息。如果你包含了assert.h头文件，你可以使用一个以布尔值或条件表达式为参数的assert函数。只要参数为真，assert函数就啥也不做。如果参数为假，assert打印一个错误信息并退出，用法如下：

void Complex::calculateCartesian ()
{
        assert (polar);
        real = mag * cos (theta);
        imag = mag * sin (theta);
        cartesian = true;
        assert (polar && cartesian);
}

第一句assert检查先决条件（事实上只是一部分先决条件），第二句assert检查后置条件。在我的开发环境中，当一个断言失败时会得到以下信息：

Complex.cpp:63: void Complex::calculatePolar(): Assertion ‘cartesian’ failed.
Abort

信息中会有许多内容可以帮助我跟踪错误，包括文件名和断言失败的出错行，断言语句的内容和所在函数名。

14.10 私有函数

在很多时候，有些成员函数是在一个类内部才会被调用到，他们不应当被使用这个类的客户代码调用。例如，calculatePolar和calculateCartesianare会被访问函数调用到，但客户代码不应该直接调用他们（虽然不会造成伤害）。如果我们想保护这些函数不被调用到，我们就需要把他们声明为private，正如我们处理变量那样。所以一个完整的复数类的定义如下：

class Complex
{
    private:
        double real, imag;
        double mag, theta;
        bool cartesian, polar;

        void calculateCartesian ();
        void calculatePolar ();

public:
        Complex () { cartesian = false;           polar = false; }

        Complex (double r, double i)
        {
                    real = r;  imag = i;
                    cartesian = true;        polar = false;
        }

        void printCartesian ();
        void printPolar ();

        double getReal ();
        double getImag ();
        double getMag ();
        double getTheta ();

        void setCartesian (double r, double i);
        void setPolar (double m, double t);
};

开头的private标号不是必须的，但它是一个有用的提示符。

14.11 术语表

类（class）：通常来说，类即带成员函数的用户自定义类型。在C++中一个类即为带私有变量的结构体。

访问函数（accessor function）：提供对私有变量的访问（读或写）功能的函数。

不变式（invariant）：一个条件，跟一个对象相关，并应该在客户代码中一直为真，该不变性应被成员函数保持。

先决条件（precondition）：在某一个函数开始假定为真的条件。如果先决条件为假，函数可能不能正常运行。最好尽可能的检查先决条件。

后置条件（postcondition）：在函数执行末尾为真的条件。

第15章 文件输入/输出与apmatrix类

15.1 流

为了从文件获取输入，或者将输出发送到文件，你需要创建ifstream对象（对应输入文件）或ofstream对象（对应输出文件）。这些类型在头文件fstream.h中定义，使用时必须包含该文件。

流是一个抽象对象，它表示从源（如键盘或文件）到目标（如屏幕或文件）的数据流动。

我们已经用过了两个流：cin和cout，其类型分别是istream和ostream。cin代表从键盘到程序的数据流。每次程序使用>>操作符或getline函数时会将数据从输入流中取走。

类似的，程序在ostream上使用<<操作符时，它将数据添加到输出流。

15.2 文件输入

为了从文件获取数据，必须创建一个从文件到程序的流对象。这点我们可以利用ifstream的构造函数实现：

ifstream infile ("file-name");

该构造函数的参数是一个字符串，即你要打开的文件的名字。其结果是创建了infile对象，它支持所有 cin上可以执行的操作，包括>>和getline。

int x;
apstring line;
infile >> x; // 读取一个整型数并保存到x中
getline (infile, line); // 读取整行并保存到line中

如果我们提前知道文件中有多少数据，那就可以直接写一个循环来读取整个文件，然后再停止。然而更常见的情况是，我们想读取整个文件，但是不知道其大小。

ifstream有几个用以检查输入流状态的成员函数，它们是good、eof、fail和bad等。我们使用good函数来确保文件成功打开，而使用eof函数来探测”文件尾“。

无论什么时候从输入流读取数据，直到检查时你才能知道尝试是否成功。如果eof函数的返回值为true，那说明已经到达文件尾，我们就知道最后一次读取尝试以失败告终。下面程序代码的功能是：读取一个文件的每一行并将其输出到屏幕上。

apstring fileName = ...;
ifstream infile (fileName.c_str());

if (infile.good() == false) {
  cout << "Unable to open the file named " << fileName;
  exit (1);
}

while (true) {
  getline (infile, line);
  if (infile.eof()) break;
  cout << line << endl;
}

函数c_str把apstring转换为原生C字符串。因为ifstream构造函数期望的参数是C字符串，所以apstring必须转换一下。

我们可以在打开文件之后，立即调用good函数。如果系统无法打开文件，该函数就返回false，原因很可能是文件不存在或者你没有文件读取权限。

while(true)是无穷循环的习惯写法。通常循环中某处会有个break语句，这样程序就不会真的永远运行下去（不过有的程序的确是希望永远执行）。这个例子中，break语句允许只要发现文件尾就退出循环。

退出循环操作放在输入语句和输出语句之间很重要，这样getline在遇到文件尾失败之后，我们就不会在line中输出无效信息。

15.3 文件输出

将输出发送到文件的方法与处理输入类似。例如，我们可以修改前面的程序以实现将一个文件逐行复制到另一个文件的功能。

ifstream infile ("input-file");
ofstream outfile ("output-file");

if (infile.good() == false || outfile.good() == false) {
  cout << "Unable to open one of the files." << endl;
  exit (1);
}

while (true) {
  getline (infile, line);
  if (infile.eof()) break;
  outfile << line << endl;
}

15.4 解析输入

在1.4节，我们把“解析”定义为分析自然语言句子或形式语言语句之结构的过程。比如，编译器在将代码翻译成机器语言程序之前必须先进行解析。

此外，当你从文件或键盘读取输入时，一般也需要进行解析，以提取想要的信息并发现错误。

例如，我有一个文件distances，其中包含了美国主要城市之间的距离信息。这些信息是我从一个随机选择的网页（http://www.jaring.my/usiskl/usa/distance.html）中得到的，所以数据可能不是很准确，不过这也没什么关系。文件格式看起来是这样的：

"Atlanta"     "Chicago"       700
"Atlanta"     "Boston"        1100
"Atlanta"     "Chicago"       700
"Atlanta"     "Dallas"        800
"Atlanta"     "Denver"        1450
"Atlanta"     "Detroit"       750
"Atlanta"     "Orlando"       400

文件中的每一行包含了两个城市的名字以及它们之间的距离，其中城市名用引号标记，距离以英里为单位。引号是有用的，因为它能让我们很容易地处理多于一个单词的城市名，如”San Francisco“（旧金山）。

通过搜索一行输入中的引号，我们能找到每个城市在该行的开始和结束位置。不过查找引号这样的特殊字符可能让人有点困惑，因为引号是C++中用于标识字符串的特殊字符。

要找到引号第一次出现的位置，应该这样写：

int index = line.find (’\"’);

参数看起来有点乱，不过它就是表示双引号字符。最外层的单引号依然用于表示这是个字符值。反斜杠（\）说明我们想使用下一个字符的字面意义。 所以序列 " 表示双引号，而序列 \’表示单引号。有趣的是， 序列\表示一个反斜杠。第一个反斜杠指示我们要认真对待第二个反斜杠。

解析输入行由这几部分组成：找到每个城市名在该行中的开始和结束位置，使用substr函数提取城市和距离信息。substr是apstring的成员函数之一，它有两个参数，分别是子串的起始位置和长度。

void processLine (const apstring& line)
{
  // 我们要查找的字符是引号
  char quote = ’\"’;

  // 将引号的索引保存在一个向量中
  apvector<int> quoteIndex (4);

  // 使用内置的find函数查找到第一个引号
  quoteIndex[0] = line.find (quote);

  // 使用第7章定义的find函数查找其他引号
  for (int i=1; i<4; i++) {
    quoteIndex[i] = find (line, quote, quoteIndex[i-1]+1);
  }

  // 将一行的内容分割成子串
  int len1 = quoteIndex[1] - quoteIndex[0] - 1;
  apstring city1 = line.substr (quoteIndex[0]+1, len1);
  int len2 = quoteIndex[3] - quoteIndex[2] - 1;
  apstring city2 = line.substr (quoteIndex[2]+1, len2);
  int len3 = line.length() - quoteIndex[2] - 1;
  apstring distString = line.substr (quoteIndex[3]+1, len3);

  // 输出提取的信息
  cout << city1 << "\t" << city2 << "\t" << distString << endl;
}

当然，我们真正想要的并不仅仅是提取并显示信息，不过这是一个好的开始。

15.5 解析数字

下一个任务是把文件中的数字从字符串形式转换为整型数。在书写较大的数字时，人们往往会用逗号将数字分组，如1,750。而计算机处理数字时，绝大部分情况是不包括逗号的，而且内置的读取数字的函数通常不能处理逗号。这就增加了转换的困难，不过也给了我们一个机会来编写去掉逗号的函数，所以这也没什么。去掉逗号之后，我们就可以使用库函数atoi将字符串转换为整型数了。atoi在头文件stdlib.h中定义。

要去掉逗号，一个选择就是遍历字符串，检查每个字符是否是数字。如果是的话，我们就将其加入结果字符串中。在循环结束时，原始字符串中的所有数字就都按顺序包含到结果字符串中了。

int convertToInt (const apstring& s)
{
  apstring digitString = "";

  for (int i=0; i<s.length(); i++) {
    if (isdigit (s[i])) {
    digitString += s[i];
    }
  }
  return atoi (digitString.c_str());
}

变量digitString是累加器的一个例子。累加器和我们在第7.9节见过的计数器比较相似，不过计数器是不断地增加值，而累加器是每次以字符串连接的方式增加一个字符。

表达式

digitString += s[i];

等价于表达式

digitString = digitString + s[i];

两条语句都是在现有字符串末尾添加一个字符。

因为atoi以一个C字符串作为参数，所以我们必须先把digitString转化为C字符串，然后才能将其作为atoi的参数。

15.6 集合数据结构Set

数据结构是一个容器，用于将一些数据组织到单个对象中。我们已经见过了几个数据结构，比如apstring是一些字符组成，而apvector是一组相同类型（可以是任意数据类型）的元素组成。

有序集是由一些项组成的集合，它有两个决定性的属性：

有序性：集合中的元素都有一个相应的索引。我们可以通过这些索引确定集合中的元素。

唯一性：集合中每个元素只能出现一次。向集合中添加一个已经存在的元素是没有效果的。

此外，我们实现的有序集还有下面一个属性：

大小任意：随着我们向集合中添加元素，它会扩充以容纳新元素。apstring和apvector都是有序的；每个元素都有一个索引，我们可以通过索引来确定元素。但是我们见到的数据结构都不具有唯一性和大小任意这两个属性。

要满足唯一性，我们编写的add函数必须先查找以确定集合中是否存在要添加的元素。集合随着添加元素扩张这一特点可以利用apvector的resize函数实现。

下面是Set类定义的开始部分：

class Set {
private:
  apvector<apstring> elements;
  int numElements;

public:
  Set (int n);

  int getNumElements () const;
  apstring getElement (int i) const;
  int find (const apstring& s) const;
  int add (const apstring& s);
};

Set::Set (int n)
{
  apvector<apstring> temp (n);
  elements = temp;
  numElements = 0;
}

实例变量包括字符串的向量和记录集合中有多少元素的整型数。一定要记住集合中的元素数numElement与apvector的大小不是一个东西。通常前者会小一些。

Set的构造函数接受一个参数，该参数是apvector的初始大小。元素个数初始值总是0。

getNumElements和getElement是私有实例变量的访问函数。 numElements是只读变量，所以我们只提供了get函数而没有提供set函数。

int Set::getNumElements () const
{
  return numElements;
}

为什么我们必须阻止客户程序修改getNumElements呢？ 因为这是该类型的不变式，客户程序怎么能破坏不变式呢。我们看下Set其余的成员函数，看你能否说服自己它们都维护了不变式。

当我们使用[]操作符访问apvector时，它会检查并确认索引值大于等于0且小于向量的长度。不过要访问集合的元素，我们需要更强的条件验证。index必须小于元素数，元素数可能是个比向量长度小的值。

apstring Set::getElement (int i) const
{
  if (i < numElements) {
    return elements[i];
  } else {
  cout << "Set index out of range." << endl;
  exit (1);
  }
}

如果getElement得到的索引值超出了范围，它会打印错误信息（我承认，并不是最有用的信息）后退出。 find和add是比较有趣的函数。到目前为止，遍历和查找的模式还是老样子：

int Set::find (const apstring& s) const
{
  for (int i=0; i<numElements; i++) {
    if (elements[i] == s) return i;
  }
  return -1;
}

现在就剩下add了。像add这样的函数的返回类型一般是void，不过在这个例子中，更有意义的可能是返回元素的索引。

int Set::add (const apstring& s)
{
  // 如果元素已经在集合中，返回其索引
  int index = find (s);
  if (index != -1) return index;

  // 如果apvector满了，将它的大小调整为原来的2倍
  if (numElements == elements.length()) {
  elements.resize (elements.length() * 2);
  }

  // 添加新元素并返回其索引
  index = numElements;
  elements[index] = s;
  numElements++;
  return index;
}

这里有个技巧，numElements会以两种方式使用：其一就是表示集合中的元素数目，其二是用作下一个要添加的元素的索引。

可能要花点时间才能相信这行得通，但是考虑一下：当元素数目为0时，下一个要加入元素的索引也是0。当元素数目等于向量的长度时，这就说明向量已经满了，要加入新元素必须先通过resize分配更多的空间。

下面是一个Set对象的状态图，该对象初始包含2个元素的空间：

现在我们可以使用Set类来记录在文件中找到的城市。在main函数中我们以2为初始大小创建Set对象：

Set cities (2);

然后在processLine函数中我们把两个城市添加到Set中，并保存返回的索引值。

int index1 = cities.add (city1);
int index2 = cities.add (city2);

我修改了processLine函数，使它以城市对象为第二个参数。

15.7 apmatrix类

apmatrix是二维的，除此之外它与apvector很像。不同于向量的长度，apmatrix有两个维度，称为numrows和numcols，分别表示“行数”和“列数”。

矩阵中的每个元素用两个索引来识别，其中一个是行编号，另一个是列编号。

要创建一个矩阵，有四种可选的构造函数：

apmatrix<char> m1;
apmatrix<int> m2 (3, 4);
apmatrix<double> m3 (rows, cols, 0.0);
apmatrix<double> m4 (m3);

第一个构造函数什么都没做，它创建的矩阵行数和列数都是0。第二个有两个整型数类型的参数，依次是行数和列数的初始值。第三个构造函数添加了一个参数用于初始化矩阵的元素，其余与第二个相同。第四个是复制构造函数，它以另一个apmatrix对象为参数。

就像apvectors一样，我们可以创建任何类型的apmatrix对象 （包括apvector，甚至apmatrix等类型）。

要访问矩阵的元素，我们使用[]操作符来指定行和列的信息：

m2[0][0] = 1;
m3[1][2] = 10.0 * m2[0][0];

如果我们想尝试访问范围之外的元素，程序会打印错误信息并退出。

numrows和numcols两个函数分别获取矩阵的行数和列数。记住，行索引是0到numrows() -1之间的数，而列索引是0和numcols() -1之间的数。

常用嵌套循环来遍历矩阵。下面循环将矩阵中每个元素的值设置为其行索引和列索引的和：

for (int row=0; row < m2.numrows(); row++) {
  for (int col=0; col < m2.numcols(); col++) {
    m2[row][col] = row + col;
  }
}

循环打印时，矩阵每一行的元素使用制表符分隔，列之间以换行符分隔：

for (int row=0; row < m2.numrows(); row++) {
  for (int col=0; col < m2.numcols(); col++) {
    cout << m2[row][col] << "\t";
  }
  cout << endl;
}

15.8 距离矩阵

最后，我们准备把数据从文件读入一个矩阵中。具体来说，每个城市在该矩阵中都一个相应的行和列。

我们将在main函数中创建该矩阵，它会剩余大量空间：

apmatrix<int> distances (50, 50, 0);

在processLine内部，我们从Set中得到两个城市的索引，并以这两个索引为矩阵的索引，向矩阵中添加了新信息：

int dist = convertToInt (distString);
int index1 = cities.add (city1);
int index2 = cities.add (city2);

distances[index1][index2] = distance;
distances[index2][index1] = distance;

最后，在main函数中我们可以将信息以可读的形式打印出来：

for (int i=0; i<cities.getNumElements(); i++) {
  cout << cities.getElement(i) << "\t";

  for (int j=0; j<=i; j++) {
    cout << distances[i][j] << "\t";
  }
  cout << endl;
}

cout << "\t";
for (int i=0; i<cities.getNumElements(); i++) {
  cout << cities.getElement(i) << "\t";
}
cout << endl;

这段代码的输出就是本章开头的矩阵。原始数据可以从本书网站获取。

15.9 一个更合理的距离矩阵

虽然这段代码可以工作，但它本可以组织的更好。既然我们已经写了一个原型，那么我们就处于评价其设计并改进之的有利位置了。

那现在的代码有些什么问题呢？

1. 我们提前不知道要创建多大的距离矩阵，所以我们选择了一个任意大的数字（50），然后创建了一个固定大小的矩阵。更好的方式是允许距离矩阵以类似Set的方式扩充，而apmatrix类的resize函数使之成为可能。
2. 矩阵中的数据没有很好的封装。我们不得不以城市名的集合与矩阵本身作为参数传给processLine，这样很不合适。再就是，因为我们没提供执行错误检查的访问函数，所以使用距离矩阵容易出错。有个好的想法是，将表示城市名的Set对象和表示距离的apmatrix对象组合到DistMatrix类中。

下面是DistMatrix类头文件大概形式的一个草稿：

class DistMatrix {
private:
  Set cities;
  apmatrix<int> distances;

public:
  DistMatrix (int rows);

  void add (const apstring& city1, const apstring& city2, int dist);
  int distance (int i, int j) const;
  int distance (const apstring& city1, const apstring& city2) const;
  apstring cityName (int i) const;
  int numCities () const;
  void print ();
};

我们可以使用这个接口来简化main函数：

void main ()
{
  apstring line;
  ifstream infile ("distances");
  DistMatrix distances (2);

  while (true) {
    getline (infile, line);
    if (infile.eof()) break;
    processLine (line, distances);
  }

  distances.print ();
}

也可以简化 processLine函数：

void processLine (const apstring& line, DistMatrix& distances)
{
  char quote = ’\"’;
  apvector<int> quoteIndex (4);
  quoteIndex[0] = line.find (quote);
  for (int i=1; i<4; i++) {
    quoteIndex[i] = find (line, quote, quoteIndex[i-1]+1);
  }

  // 将行分割为子串
  int len1 = quoteIndex[1] - quoteIndex[0] - 1;
  apstring city1 = line.substr (quoteIndex[0]+1, len1);
  int len2 = quoteIndex[3] - quoteIndex[2] - 1;
  apstring city2 = line.substr (quoteIndex[2]+1, len2);
  int len3 = line.length() - quoteIndex[2] - 1;
  apstring distString = line.substr (quoteIndex[3]+1, len3);
  int distance = convertToInt (distString);

  // 将新数据添加到距离矩阵中
  distances.add (city1, city2, distance);
}

我把实现DistMatrix类的成员函数留作练习请读者完成。

15.10 术语表

有序集（ordered set）：指一种数据结构，其中每个元素只出现一次，而且每个元素都有一个索引来标识它。

流（stream）：表示从一个位置到另一个位置的数据流或数据序列的数据结构。C++ 中流用来表示输入和输出。

累加器（accumulator）：循环中用于累加结果的变量，一般每次迭代过程会在该变量后添加或连接一些东西。