Finite Basis Physics-Informed Neural Networks (FBPINNs) a scalable domain decomposition approa
@[TOC](论文阅读:Finite Basis Physics-Informed Neural Networks (FBPINNs) a scalable domain decomposition approach for solving differential equations)
Finite Basis Physics-Informed Neural Networks (FBPINNs) a scalable domain decomposition approach for solving differential equations
动机
PINN方法的一个难点就是将其推广到大域中,考虑如下方程:
d u d x = cos ( ω x ) , u ( 0 ) = 0 \begin{aligned} \frac{du}{dx}&=\cos(\omega x),\\ u(0)&=0 \end{aligned} dxduu(0)=cos(ωx),=0
其中: x , u , ω ∈ R 1 x,u,\omega\in\mathbb{R}^1 x,u,ω∈R1 ,这个PDE的精确解为:
u ( x ) = 1 ω sin ( ω x ) u(x)=\frac1\omega\sin(\omega x) u(x)=ω1sin(ωx)
通过如下变换,可给PINN施加精确边界条件:
u ^ ( x ; θ ) = tanh ( ω x ) N N ( x ; θ ) \hat{u}(x;\theta)=\tanh(\omega x)NN(x;\theta) u^(x;θ)=tanh(ωx)NN(x;θ)
于是,PINN的损失函数可表示如下:
L ( θ ) = L p ( θ ) = 1 N p ∑ i N p ∥ d d x u ^ ( x i ; θ ) − cos ( ω x i ) ∥ 2 \mathcal{L}(\theta)=\mathcal{L}_p(\theta)=\frac1{N_p}\sum_i^{N_p}\|\frac d{dx}\hat{u}(x_i;\theta)-\cos(\omega x_i)\left\|^2\right. L(θ)=Lp(θ)=Np1i∑Np∥dxdu^(xi;θ)−cos(ωxi) 2

上图为作者对上述方程进行的试验。可以从图中看到,当频率 ω \omega ω 较低的时候,PINN能够很好地对解进行近似;但当频率增大时,PINN就出现了失效的情况,使用更大的网络才有可能获得较为准确的解。
虽然 PINN 在低频下表现良好,但它很难扩展到更高的频率;频率越高的 PINN 需要的自由参数越多,收敛速度越慢,精度也越差。多个重要且相关的因素导致了这个问题。一是随着解决方案复杂度的增加,网络需要更多的自由参数来准确地表示它,从而使优化问题变得更加困难。另一个问题是,随着频率的增加,需要更多的训练样本点来充分采样域,这又使优化问题变得更加困难。第三是神经网络的谱偏差,这是神经网络倾向于学习高频的速度比学习低频慢得多,这一特性已经过严格研究。使这些因素更加复杂的事实是,随着网络规模、训练点数量和收敛时间的增长,所需的计算资源显着增加。
值得注意的是,对于这个问题,缩放到更高的频率相当于缩放到更大的域大小。所以保持 ω = 1 \omega = 1 ω=1 但将域大小扩大 15 倍 与将 ω \omega ω 更改为 15 其实是一样的。事实上,增加域大小和缩放到更高的频率是相关问题,上述案例研究强调了 PINN 的一般观察:随着域大小的增加,PINN 优化通常变得更加困难,并且需要更长的时间才能完成收敛。
FBPINN
FBPINN 工作流程如上图所示。在 FBPINN 中,问题域被划分为重叠的子域。神经网络被放置在每个子域内,使得在子域的中心内,网络学习完整的解决方案,而在重叠区域中,解决方案被定义为所有重叠网络的总和。在求和之前,每个网络都乘以一个平滑、可微的窗口函数,该函数将其局部限制在其子域内。除此之外,每个网络的输入变量在每个子域上分别标准化,并且可以定义灵活的训练计划,限制在每个梯度下降训练步骤中更新哪些子域网络。
对于任何域分解技术,确保各个神经网络解决方案在子域接口之间进行通信和匹配非常重要。在 FBPINN 中,在训练期间,神经网络在子域之间的重叠区域中共享其解决方案,并且通过将全局解决方案构建为这些解决方案的总和,自动确保解决方案在子域之间是连续的。与其他域分解方法相比,这种方法允许 FBPINN 使用与 PINN 类似的损失函数,而不需要使用额外的界面损失项。
数学描述
在 FBPINN 中,问题域 Ω ⊂ R d \Omega\subset\mathbb{R}^d Ω⊂Rd 被细分为 n n n 个重叠的子域 Ω i ⊂ Ω \Omega_i\subset{\operatorname*{\Omega}} Ωi⊂Ω。 FBPINN 可以使用任何类型的细分(规则或不规则)以及任何重叠宽度,只要子域重叠即可。为简单起见,作者在后续工作中使用常规超矩形划分。
给定子域定义,FBPINN 的解可表示如下:
u ^ ( x ; θ ) = C [ N N ‾ ( x ; θ ) ] \hat{u}(x;\theta)=\mathcal{C}\left[\overline{NN}(x;\theta)\right] u^(x;θ)=C[NN(x;θ)]
其中,
N N ‾ ( x ; θ ) = ∑ i n w i ( x ) ⋅ unnorm ∘ N N i ∘ norm i ( x ) \overline{NN}(x;\theta)=\sum_i^nw_i(x)\cdot\text{unnorm}\circ NN_i\circ\text{norm}_i(x) NN(x;θ)=i∑nwi(x)⋅unnorm∘NNi∘normi(x)
N N i ( x ; θ i ) NN_i(x;\theta_i) NNi(x;θi) 是放置在每个子域 Ω i \Omega_i Ωi 中的独立神经网络, w i ( x ) w_i(x) wi(x) 是平滑、可微的窗口函数,将每个网络局部限制在其子域中, C \mathcal{C} C 是约束算子,添加适当的“硬”约束转换网络输出,使其满足边界条件。 n o r m i \mathrm{norm}_i normi 表示每个子域中输入向量 x x x 的单独归一化,unnorm 表示应用于每个神经网络输出的公共非归一化,并且 θ = { θ i } \theta=\{\theta_i\} θ={θi}。
窗函数的目的是将每个神经网络解 NNi 局部限制在其子域内。可以使用任何可微函数,只要它在子域之外接近零并且在子域内大于零。对于本文研究的超矩形子域,作者使用以下窗函数:
w i ( x ) = ∏ j d ϕ ( ( x j − a i j ) / σ i j ) ϕ ( ( b i j − x j ) / σ i j ) w_i(x)=\prod_j^d\phi((x^j-a_i^j)/\sigma_i^j)\phi((b_i^j-x^j)/\sigma_i^j) wi(x)=j∏dϕ((xj−aij)/σij)ϕ((bij−xj)/σij)
其中 j j j 表示输入向量的每个维度, a i j a_{i}^{j} aij和 b i j b_{i}^{j} bij 表示每个维度左右重叠区域的中点(其中 a i j < b i j a_{i}^{j} < b_{i}^{j} aij<bij ), ϕ ( x ) = 1 1 + e − x \phi(x)~=~\frac1{1+e^{-x}} ϕ(x) = 1+e−x1 是 sigmoid 函数, σ i j \sigma_{i}^{j} σij 是一组参数,其定义使得窗口函数在重叠区域之外为零(可忽略不计地接近)。每个子域中的单独归一化范数是通过在输入到网络之前对子域上每个维度中 [ − 1 , 1 ] [−1, 1] [−1,1] 之间的输入向量进行归一化来应用的,同时选择公共输出非归一化非范数,以便每个神经网络输出保持不变在 [ − 1 , 1 ] [−1, 1] [−1,1] 范围内,并且取决于解本身。任何神经网络都可以用来定义 N N i ( x ; θ i ~ ) NN_{\boldsymbol{i}}(x;\tilde{\theta_{i}}) NNi(x;θi~);为了简单起见,在本文中作者只考虑全连接的神经网络。
施加精确边界条件的PINN损失可表示如下:
L ( θ ) = L p ( θ ) = 1 N p ∑ i N p ∣ ∣ D [ u ^ ( x i ; θ ) ; λ ] − f ( x i ) ∣ ∣ 2 \mathcal{L}(\theta)=\mathcal{L}_p(\theta)=\frac1{N_p}\sum_i^{N_p}||\mathcal{D}[\hat{u}(x_i;\theta);\lambda]-f(x_i)||^2 L(θ)=Lp(θ)=Np1i∑Np∣∣D[u^(xi;θ);λ]−f(xi)∣∣2
使用在全域 Ω \Omega Ω 上采样的一组训练点 x i {x_i} xi。
灵活的训练计划
除了之前描述的将 PINN 扩展到大域的问题之外,另一个问题是难以确保远离边界学习的 PINN 解与边界条件一致。更准确地说,可以想象,在训练的早期,PINN 可能会关注与远离边界的域中的边界条件不一致的特定解,因为网络尚未学习到一致的解。解决方案更接近边界以约束它。通过学习两个不同的特定解决方案,优化问题可能最终出现局部最小值,从而导致更难的优化问题。因此,对于某些问题,以类似于经典方法中采用的时间推进方案的方式从边界“向外”顺序学习解决方案可能是有意义的。
FBPINN 允许此类功能,由于其域分解,该功能很容易实现。在训练过程中的任何时候,都可以限制更新哪些子域网络,因此可以设计灵活的训练计划来适应特定的边界问题。
上图展示了一个示例训练计划。在训练计划中,可以定义“活动”模型,即当前正在更新的网络,“固定”模型,即已经过训练且其自由参数已固定的网络,以及“非活动”模型,它们是尚未训练的网络。在每个训练步骤中,只有活动模型及其固定邻居对 FBPINN中的求和做出贡献,并且仅对活动子域内的训练点进行采样。
并行训练
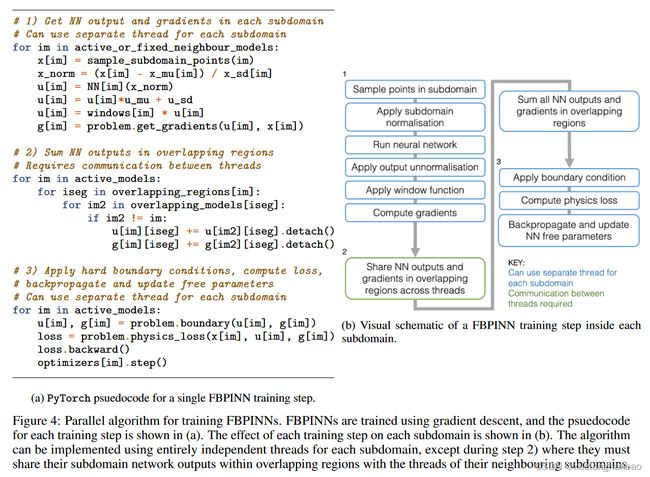
FBPINN 优化问题是通过使用梯度下降来解决的,与 PINN 类似。这可以在单个全局优化循环中简单地实现,但在实践中,我们可以利用域分解以高度并行和数据效率更高的方式训练 FBPINN。
并行化 FBPINN 时有两个关键考虑因素。首先,在每个神经网络的子域之外,应用窗函数后,其输出始终为零,这意味着子域之外的训练点在更新其自由参数时将提供零梯度。因此,只需要每个子域内的训练点来训练每个网络,这使得训练的数据效率更高。其次是每个训练步骤的多个部分可以并行实施;在计算相对于输入向量的输出和梯度时,可以使用每个网络的单独线程,并且一旦对重叠区域中的网络输出进行求和,就可以使用每个网络的单独线程来反向传播损失函数并更新他们的自由参数。这使得训练时间大大减少。
实验结果
一维正弦实验
同样考虑如下问题:
d u d x = cos ( ω x ) , u ( 0 ) = 0 \begin{aligned} \frac{du}{dx}&=\cos(\omega x),\\ u(0)&=0 \end{aligned} dxduu(0)=cos(ωx),=0
上图为 ω = 1 \omega=1 ω=1 时的训练结果
上图为 ω = 15 \omega=15 ω=15 的结果,整个域被分为30个子域,可以看到,FBPINN成功学习到了真解,相比于PINN在5层128个神经元,共66433个可训练参数下才能较好近似,FBPINN的参数量不过翻了30倍,为9630个。
二阶微分实验
考虑如下问题:
d 2 u d x 2 = sin ( ω x ) , u ( 0 ) = 0 , d u d x ( 0 ) = − 1 ω , \begin{aligned} \frac{d^2u}{dx^2}& =\sin(\omega x), \\ u(0)& =0, \\ \frac{du}{dx}(0)& =-\frac{1}{\omega}, \end{aligned} dx2d2uu(0)dxdu(0)=sin(ωx),=0,=−ω1,
其精确解为:
u ( x ) = − 1 ω 2 sin ( ω x ) u(x)=-\frac{1}{\omega^2}\sin(\omega x) u(x)=−ω21sin(ωx)
作者使用如下输出变换使其满足强制边界条件:
u ^ ( x ; θ ) = − 1 ω 2 tanh ( ω x ) + tanh 2 ( ω x ) N N ‾ ( x ; θ ) \hat{u}(x;\theta)=-\frac{1}{\omega^2}\tanh(\omega x)+\tanh^2(\omega x)\overline{NN}(x;\theta) u^(x;θ)=−ω21tanh(ωx)+tanh2(ωx)NN(x;θ)
从上图可以看出尽管 FBPINN 能够捕获其所有周期,但这两种方法都难以准确地对解决方案进行建模。虽然这两个模型都能在边界条件附近准确地学习解,但在边界条件之外却很难学习。一种解释是,这两种模型都存在集成错误。二阶导数中的小错误(在损失函数中受到惩罚)可能会导致解决方案出现大错误。事实上,这两个模型都学习了更准确的二阶导数。另一种解释是,远离边界,FBPINN 和 PINN 专注于基础方程的不同(且不正确)特定解。特别是,远离边界时,FBPINN 解似乎与输入变量的线性函数叠加,这是该微分方程下的可行解(但与边界条件不一致)。
二维正弦实验
考虑如下PDE:
∂ u ∂ x 1 + ∂ u ∂ x 2 = cos ( ω x 1 ) + cos ( ω x 2 ) , u ( 0 , x 2 ) = 1 ω sin ( ω x 2 ) , \begin{aligned} \begin{aligned}\frac{\partial u}{\partial x_1}+\frac{\partial u}{\partial x_2}\end{aligned}& =\cos(\omega x_1)+\cos(\omega x_2), \\ u(0,x_{2})& =\frac1\omega\sin(\omega x_2), \end{aligned} ∂x1∂u+∂x2∂uu(0,x2)=cos(ωx1)+cos(ωx2),=ω1sin(ωx2),
其中, x = ( x 1 , x 2 ) ∈ R 2 , u ∈ R 1 x=(x_1,x_2)\in\mathbb{R}^2,u\in\mathbb{R}^1 x=(x1,x2)∈R2,u∈R1 , x 1 ∈ [ − 2 π , 2 π ] , x 2 ∈ [ − 2 π , 2 π ] . x_1\in[-2\pi,2\pi],x_2\in[-2\pi,2\pi]. x1∈[−2π,2π],x2∈[−2π,2π]. 其精确解为:
u ( x 1 , x 2 ) = 1 ω sin ( ω x 1 ) + 1 ω sin ( ω x 2 ) . u(x_1,x_2)=\frac1\omega\sin(\omega x_1)+\frac1\omega\sin(\omega x_2). u(x1,x2)=ω1sin(ωx1)+ω1sin(ωx2).
作者使用如下输出变换:
u ^ ( x 1 , x 2 ; θ ) = 1 ω sin ( ω x 2 ) + tanh ( ω x 1 ) N N ‾ ( x 1 , x 2 ; θ ) \hat{u}(x_1,x_2;\theta)=\frac1\omega\sin(\omega x_2)+\tanh(\omega x_1)\overline{NN}(x_1,x_2;\theta) u^(x1,x2;θ)=ω1sin(ωx2)+tanh(ωx1)NN(x1,x2;θ)

总结
这篇文章提出了一种类似有限元的窗口函数,将不同子域重叠部分加权相加,避免了在损失中添加界面条件的软约束项。
感觉还是挺有意思的,但实现难度也可以想象,目前官方代码只实现了N维矩形区域的域分解方法,对于其他形状还没有支持。
相关链接:
- 原文:[2107.07871] Finite Basis Physics-Informed Neural Networks (FBPINNs): a scalable domain decomposition approach for solving differential equations (arxiv.org)
- 代码:benmoseley/FBPINNs: Solve forward and inverse problems related to partial differential equations using finite basis physics-informed neural networks (FBPINNs) (github.com)