A Sequential Meta-Transfer (SMT) Learning to Combat Complexities of Physics-Informed Neural Networks
论文阅读:A Sequential Meta-Transfer SMT Learning to Combat Complexities of Physics-Informed Neural Networks Application to Composites Autoclave Processing
- A Sequential Meta-Transfer (SMT) Learning to Combat Complexities of Physics-Informed Neural Networks Application to Composites Autoclave Processing
-
- 简介
-
- 元学习
- Sequential Meta-Transfer (SMT) Learning and Composites Processing Case Study
-
- PINN中的顺序学习
- 元迁移学习
- 自适应时间分割
- 实验结果
-
- 热压罐加工
- PINN、TM以及bc-PINN对比
- 评估顺序元迁移学习的快速任务适应
- 总结
A Sequential Meta-Transfer (SMT) Learning to Combat Complexities of Physics-Informed Neural Networks Application to Composites Autoclave Processing
简介
顺序学习已经被证明是解决复杂非线性系统中 PINN 缺点的有效工具。然而,它大大增加了计算成本,因为它引入了更多的损失项,并且需要在一组时间间隔内训练多个网络。这可能会导致训练缓慢,并限制此类策略在使用 PINN 解决现实世界复杂问题时的应用。此外,虽然一些工作利用了知识可转移性(例如,通过利用 TL 和类似方法)来提高 PINN 的训练和实现效率,但迄今为止,还没有关于通过知识迁移来降低计算成本和提高顺序学习策略的适应性进行显着的研究。
本文的工作旨在开发一种新颖的顺序元迁移(SMT)学习方法,以便在具有长时域的高度非线性系统中更高效、适应性强和准确地训练 PINN。也就是说,SMT 结合并利用了众所周知的 TL 和元学习原理,但在顺序学习模式下,使 PINN 的训练比传统 PINN 更快、更高效,同时确保对其他相关任务/系统的高度适应性。在每个时间段,不是训练特定于任务的网络,而是训练一系列元学习器,其目标是获得一组最佳初始参数,用于快速适应一系列相关任务(例如,不同的边界条件配置) )。该工作还首次引入了“自适应时间分段”策略,该策略自适应地选择下一个时间间隔的跨度进行训练。对于每个时间间隔,它评估在前一个时间段上训练的子网络的性能,作为衡量两个域之间的相似性(例如,如果任务相似,则模型应该在两个域上都表现良好),并据此选择间隔的长度。这通过分配向域中不太困难的区域迈出一大步,并对具有高度非线性行为的区域采用更精细的时间间隔。
元学习
元学习是使模型能够从一组相关任务中学习,以实现快速泛化和适应新任务的目标。这与传统的机器学习相反,在传统的机器学习中,模型是使用大型数据集针对特定任务进行训练的。凭借其学习到学习的机制,元学习学会从相关任务中积累经验,并利用它来使用一些数据点来改进新任务的学习。训练元学习模型会产生一组最佳参数,这些参数可用于初始化基础学习器以快速适应新任务。为了完成这项任务,基于梯度的元学习模型采用了双层优化过程。特别是,“内部”优化负责学习给定的任务(基础学习器),而“外部”算法则以改进元训练目标(元学习器)的方式更新基础学习器。与模型无关的元学习(MAML)作为这一类别中最著名的方法,旨在学习一组初始参数,这些初始参数只需要几个梯度步骤即可学习新任务。
为了训练元学习模型,需要考虑训练任务 p ( T ) p(\mathcal{T}) p(T) 的分布。每个任务 T i \mathcal{T}_i Ti 均由数据集 Di 组成,该数据集 D i \mathcal{D}_i Di 分为训练集 D i t r \mathcal{D}^{tr}_i Ditr 和测试集 D i t e s t \mathcal{D}^{test}_i Ditest 。形式上,考虑由参数化函数 f θ f^{\theta} fθ 表示的元学习器模型(例如神经网络)。训练从元学习双层优化的内部步骤开始。具体来说,任务 T i \mathcal{T}_i Ti 从 p ( T ) p(\mathcal{T}) p(T) 中提取,并使用训练数据 D i t r \mathcal{D}^{tr}_i Ditr 和相应的训练损失值 L T i ( θ , D i t r ) \mathcal{L}_{\mathcal{T}_i}(\theta,\mathcal{D}^{tr}_i) LTi(θ,Ditr) 更新模型参数 θ \theta θ(例如,通过一次梯度更新):
θ i ′ ← θ − α ∇ θ L T i ( θ , D i t r ) \theta_i^{\prime}\leftarrow\theta-\alpha\nabla_\theta\mathcal{L}_{\mathcal{T}_i}\left(\theta,\mathcal{D}_i^{tr}\right) θi′←θ−α∇θLTi(θ,Ditr)
其中 α \alpha α 是基础学习器的步长。然后,更新后的参数 θ i ′ \theta '_i θi′ 用于针对测试集 $\mathcal{L}_{\mathcal{T}_i}(\theta’,\mathcal{D}^{test}_i) $ 评估模型性能。这里的目标是利用 D i t r \mathcal{D}^{tr}_i Ditr 来学习特定于任务的参数,从而最大限度地减少测试集的损失值。对训练期间从 p ( T ) p(\mathcal{T}) p(T) 中提取的所有任务重复此过程。接下来,在外循环优化中,使用内循环训练阶段使用的所有任务计算出的测试损失 { L T i ( θ i ′ , D i t e s t ) } T i ∈ p ( T ) 1 \left\{\mathcal{L}_{\mathcal{T}_i}\left(\theta_i^{\prime},\mathcal{D}_i^{test}\right)\right\}_{\mathcal{T}_i\in p(\mathcal{T})}^{1} {LTi(θi′,Ditest)}Ti∈p(T)1 来优化元学习器的参数 θ \theta θ,如下所示:
θ ← θ − β ∇ θ ∑ T i ∈ p ( T ) L T i ( θ i ′ , D i t e s t ) \theta\leftarrow\theta-\beta\nabla_\theta\sum_{\mathcal{T}_i\in p(\mathcal{T})}\mathcal{L}_{\mathcal{T}_i}\left(\theta_i^{\prime},\mathcal{D}_i^{test}\right) θ←θ−β∇θTi∈p(T)∑LTi(θi′,Ditest)
其中 β \beta β 是元学习器的步长。一旦经过训练,基础学习器就可以用作学习新任务的最佳初始化状态,并只需要有少量的梯度步骤和少量的样本。
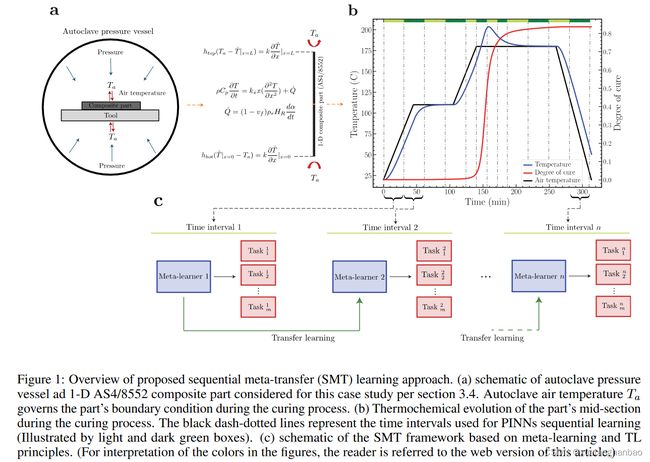
Sequential Meta-Transfer (SMT) Learning and Composites Processing Case Study
对于SMT框架,如上图所示,长时域首先被分解为小区间。利用自适应时间分段,时域被划分为更精细的时间间隔,其中系统表现出高度非线性行为。然后,在每个时间段,不是学习特定于任务的网络参数,而是训练子元学习器来学习一组最佳初始参数,从而能够快速适应一系列相关任务(例如,不同的边界条件配置) )。与传统的 PINN 相比,这被认为是一个主要优势,因为系统设置的微小变化就需要从头开始训练模型。另一方面,使用 SMT 训练的 PINN 可以使用显着更少的训练迭代(即梯度步骤)来适应新的配置。子元学习器以顺序方式进行训练(图 c)。一旦每个子学习器被训练,它就被用来初始化下一个时间间隔的元学习器(通过 TL)。由于之前时间间隔中学习的任务与当前任务相似(即,物理原理保持不变,而初始条件和边界条件略有变化),因此从先前学习的元学习器转移知识可以极大地促进以下训练过程时间段,从而进一步提高时间和计算效率。另一方面,转移的元学习器很容易针对新的初始条件和边界条件进行微调。
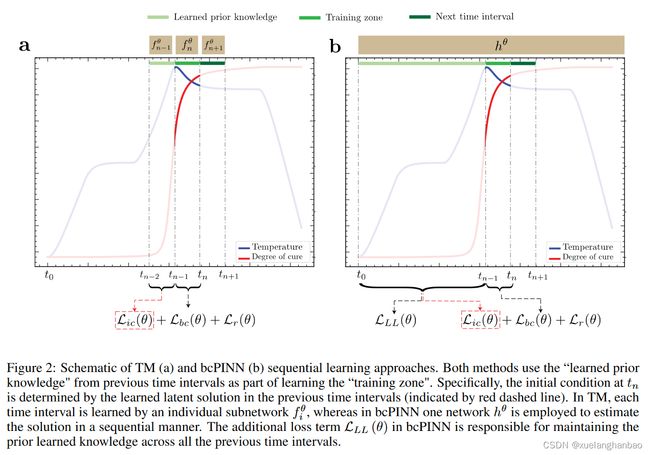
PINN中的顺序学习
TM和bc-PINN这两种方法都围绕这样的想法:将时域分解为小段有利于高度非线性系统的 PINN 训练。具体来说,在TM中,时域被划分为 n n n 个时间间隔。对于每个时间间隔 [ t i − 1 , t i ] [t_{i−1}, t_i] [ti−1,ti],分配一个子网络 f i θ f^\theta _i fiθ。训练从第一个时间间隔 [ t 0 , t 1 ] [t_0, t_1] [t0,t1] 开始,使用系统在 t = 0 t = 0 t=0 时的初始条件。训练完 f 1 f_1 f1 后,其在 t 1 t_1 t1 处的预测将用作第二个时间间隔 [ t 1 , t 2 ] [t_1, t_2] [t1,t2] 的初始条件训练第二个子网络 f 2 f_2 f2。重复此过程,直到学习到所有时间间隔的解,然后组合各个子网络以提供时域内任何点的预测。与TM相反,在bc-PINN中,仅使用一个网络以顺序方式学习长时域。这是通过引入额外的损失项来完成的,该损失项确保网络保留从先前时间段学到的知识。具体来说,一个新的损失项被添加到 PINN 的损失函数中,以满足所有先前时间间隔的解:
L ( θ ) = λ i c L i c ( θ ) + λ b c L b c ( θ ) + λ r L r ( θ ) + λ L L L L L ( θ ) \mathcal{L}\left(\theta\right)=\lambda_{ic}\mathcal{L}_{ic}\left(\theta\right)+\lambda_{bc}\mathcal{L}_{bc}\left(\theta\right)+\lambda_{r}\mathcal{L}_{r}\left(\theta\right)+\lambda_{LL}\mathcal{L}_{LL}\left(\theta\right) L(θ)=λicLic(θ)+λbcLbc(θ)+λrLr(θ)+λLLLLL(θ)
其中, L L L \mathcal{L}_{LL} LLL 表示网络在先前时间间隔内偏离已学习解决方案的损失。在每个时间步进行训练后,学习到的权重用于对相同时间间隔的一些随机数据点进行预测,并将预测存储为“真实”标签,以便在训练后续时间间隔时用于计算 L L L \mathcal{L}_{LL} LLL。与 TM 类似,时域最初被分为 n n n 个时间段。在每个时间步,网络参数 θ \theta θ 都经过训练/微调,以通过初始条件、边界条件和 PDE 损失分量学习底层解决方案,同时确保使用添加的损失项保留先前时间步的知识。这意味着,为了学习时间间隔 [ t n − 1 , t n ] [t_{n−1}, t_n] [tn−1,tn],bcPINN 需要访问网络在所有先前学习的时间间隔 [ 0 , t n − 1 ] [0, t_{n−1}] [0,tn−1] 中的预测。这与 TM 不同,TM 中仅学习潜在解前一个时间间隔 [ t n − 2 , t n − 1 ] [t_{n−2}, t_{n−1}] [tn−2,tn−1]
元迁移学习
上述顺序学习方法侧重于学习 PDE 系统的具体实现。例如,可以使用 TM 方法通过在多个时间间隔上训练子网络来捕获具有一组特定配置(即初始和边界条件以及材料属性)的高压釜中复合材料零件的非线性热化学行为。然而,所提出的 SMT 方法旨在训练一个模型,使 PINN 能够高效、快速地适应任务的分布。为了实现这一目标,TM 方法中的子网络被元学习器取代,并使用支持集进行训练,该支持集由一组为训练定义的任务目标组成,具体来说,在本研究中,通过修改边界条件参数来定义各种任务。
元学习的一个特殊限制是该方法在处理分布外任务时表现不佳。当这些任务引入剧烈的领域转变时,这一点变得更加明显。在 PINN 的顺序学习中尤其如此,其中从一个时间间隔过渡到另一个时间间隔可能会导致初始/边界条件和系统行为的显着差异。在这种情况下,人们可能需要在每个时间间隔从头开始训练元学习器,以确保有效适应新任务。然而,这在 PINN 的顺序学习设置中可能是不可行的,因为从头开始在多个时间间隔内训练元学习器非常费力且耗时。一种解决方案是将所学到的知识从手头经过训练的元学习器转移到在接下来的时间间隔内训练后续元学习器。这里采用元迁移学习策略来使所提出的顺序框架的训练更加高效。特别是,训练从使用第一个时间间隔 [ 0 , t 1 ] [0, t_1] [0,t1] 的初始条件和边界条件训练第一个元学习器 (ML1) 开始。训练完成后,ML1 的学习权重用于初始化在第二时间间隔 [ t 1 , t 2 ] [t_1,t_2] [t1,t2] 训练的第二个元学习器 (ML2)。重复这个过程,直到与所有时间间隔相关的元学习器都被训练完毕。
自适应时间分割
事实证明,顺序学习方法可以有效地准确学习边界条件快速变化和扭结的区域或潜在解函数中高度非线性行为的区域(例如复合材料加工中的温度和 DoC)。研究还表明,采用较小的时间段大小可以显着提高 PINN 的性能。然而,这需要付出更多计算成本的代价,因为它需要训练更多的子网络。因此,人们希望避免使时间间隔太小。为了确保分段长度与系统行为的复杂性适当成比例,并避免不必要的计算开销,实施以下自适应分段策略。最初,时域被分为 n n n 个长度相等的段,训练从第一个间隔开始。一旦第一个子网训练并达到理想的训练/测试损失后,优化的权重将被转移以初始化下一个子网络。然后,在开始训练之前,计算新子网络(具有初始化权重)在第二时间间隔的训练损失。损失值可以被视为源任务和目标任务之间的差异程度以及目标任务的难度级别(例如,在非线性方面)的代表。然后将新任务的损失值与前一个任务(源)的训练损失进行比较,如果差异超过用户定义的阈值 ϵ \epsilon ϵ,则新时间段的损失值减半,新时间段的损失值(现在)与原始尺寸的一半长度)进行计算和比较。重复此步骤,直到达到可接受的初始损失,然后开始训练过程。自适应分割方法的好处有两个。首先,减少时间间隔的长度使得“刚性”和高度非线性系统的训练变得更容易。其次,从TL的角度来看,使用源网络权重的目标任务的较大损失值表明源任务和目标任务之间存在相当大的差异(这里是相邻的时间间隔),因此,TL性能很差。通过缩短时间间隔,距离源域较远的点被删除,这导致目标域的输入空间更接近最重要的是,该策略确保更多的计算能力仅分配给“困难”区域。
实验结果
热压罐加工
热压罐加工是先进复合材料结构制造中广泛采用的方法。在此过程中,复合材料部件经历预定义的温度和压力循环,称为“固化循环”,具有由高压釜空气温度强制执行的多个加热斜坡和等温阶段。目标是固化树脂基体从而获得最佳的树脂纤维分布,并将空隙/缺陷的发生降至最低。制造零件的质量在很大程度上取决于工艺配置以及所用原材料的特性。温度和 DoC(表示树脂的化学进步)是复合材料制造中的两个关键状态变量,不仅影响零件的热化学行为,还影响树脂流动、零件的残余应力传播和变形。固化过程、零件温度和 DoC 表现出快速变化的非线性演变。
复合材料在固化过程中的热化学行为由各向异性热传导方程控制,该方程配备了代表树脂基体放热固化反应的内生热项 Q ˙ \dot{Q} Q˙
∂ ∂ t ( ρ C p T ) = ∂ ∂ x ( k x x ∂ T ∂ x ) + ∂ ∂ y ( k y y ∂ T ∂ y ) + ∂ ∂ z ( k z z ∂ T ∂ z ) + Q ˙ \begin{aligned}\frac{\partial}{\partial t}\left(\rho C_pT\right)&=\frac{\partial}{\partial x}\left(k_{xx}\frac{\partial T}{\partial x}\right)+\frac{\partial}{\partial y}\left(k_{yy}\frac{\partial T}{\partial y}\right)+\frac{\partial}{\partial z}\left(k_{zz}\frac{\partial T}{\partial z}\right)+\dot{Q}\end{aligned} ∂t∂(ρCpT)=∂x∂(kxx∂x∂T)+∂y∂(kyy∂y∂T)+∂z∂(kzz∂z∂T)+Q˙
其中, ρ \rho ρ 表示零件密度, C p C_p Cp 表示比热容, k i i k_{ii} kii 表示各向异性导热系数。它们可以通过树脂特性和纤维特性以及纤维体积分数来计算。上式中的发热项 Q ˙ \dot{Q} Q˙ 可表示为:
Q ˙ = d α d t ( 1 − v f ) ρ r H R \dot{Q}=\frac{d\alpha}{dt}\left(1-v_f\right)\rho_rH_R Q˙=dtdα(1−vf)ρrHR
其中 α \alpha α 代表树脂的 DoC, v f v_f vf 是纤维体积分数, ρ r \rho_r ρr 是树脂密度, H R H_R HR 是树脂反应热,是完整树脂固化周期中产生的总热量的量度。 d α , d t d\alpha, dt dα,dt 是固化反应速率,它由树脂体系的固化动力学控制。对于一维传热系统,方程可以简化为:
ρ C p ∂ T ∂ t = k x x ∂ 2 T ∂ x 2 + ( 1 − v f ) ρ r H R d α d t \rho C_p\frac{\partial T}{\partial t}=k_{xx}\frac{\partial^2T}{\partial x^2}+\left(1-v_f\right)\rho_rH_R\frac{d\alpha}{dt} ρCp∂t∂T=kxx∂x2∂2T+(1−vf)ρrHRdtdα
对于具有热固性树脂体系的复合材料体系的固化过程,固化速率 d α , d t d\alpha,dt dα,dt 由树脂的固化动力学决定,通常被描述为常微分方程。特别是对于 8552 环氧树脂(本文使用的树脂系统),固化动力学已在之前的研究中得到发展,可以表示为:
d α d t = K α m ( 1 − α ) n 1 + e C { α − ( α C 0 + α C T T ) } , K = A e − Δ E R T \frac{d\alpha}{dt}=\frac{K\alpha^m(1-\alpha)^n}{1+e^{C\{\alpha-(\alpha_{C0}+\alpha_{CT}T)\}}},K=Ae^{-\frac{\Delta E}{RT}} dtdα=1+eC{α−(αC0+αCTT)}Kαm(1−α)n,K=Ae−RTΔE
其中 Δ E \Delta E ΔE 为活化能, R R R 为气体常数, α C 0 、 α C T 、 m 、 n \alpha C0、\alpha CT 、m、n αC0、αCT、m、n 和 A A A 为实验确定的常数。下表总结了本研究中固化动力学方程中使用的参数值
| 参数 | 描述 | 数值 |
|---|---|---|
| Δ E \Delta E ΔE | 活化能 | 66.5 (kJ/gmol) 66.5\text{(kJ/gmol)} 66.5(kJ/gmol) |
| R R R | 气体常数 | 8.314 8.314 8.314 |
| A A A | 指数前固化率系数 | 1.53 ∗ 1 0 5 (1/s) 1.53*10^5\text{(1/s)} 1.53∗105(1/s) |
| m m m | 第一指数常数 | 0.813 0.813 0.813 |
| n n n | 第二指数常数 | 2.74 2.74 2.74 |
| C C C | 扩散常数 | 43.1 43.1 43.1 |
| α C 0 \alpha_{C0} αC0 | T = 0 K T = 0 K T=0K 时的临界固化程度 | − 1.684 -1.684 −1.684 |
| α C T \alpha_{CT} αCT | 临界树脂固化度常数 | 5.475 ∗ 1 0 − 3 (1/K) 5.475*10^{-3}\text{(1/K)} 5.475∗10−3(1/K) |
上述耦合系统的初始条件可以指定为:
T ∣ t = 0 = T 0 ( x ) α ∣ t = 0 = α 0 ( x ) \begin{aligned}T\mid_{t=0}&=T_0\left(x\right)\\ \alpha\mid_{t=0}&=\alpha_0\left(x\right)\end{aligned} T∣t=0α∣t=0=T0(x)=α0(x)
T 0 T_0 T0 表示零件的初始温度,通常被认为在整个零件中是均匀的。本研究假设固化过程开始时零件的温度为 20 ° C 20\degree C 20°C。 α 0 \alpha_0 α0 是树脂系统的初始 DoC,对于未固化的部件,假设为零或很小的值(在本研究中,假设值为 0.001。)
边界条件也可以通过固化周期配方规定的高压釜空气温度 T a ( t ) T_a (t) Ta(t) 来指定。具体来说,Robin 边界条件可以定义为包含复合材料部件和高压釜空气之间的对流换热
h t ( T a ( t ) − T ∣ x = L ) = k x x ∂ T ∂ x ∣ x = L h b ( T ∣ x = 0 − T a ( t ) ) = k x x ∂ T ∂ x ∣ x = 0 \begin{aligned}h_t\left(T_a(t)-T\mid_{x=L}\right)&=k_{xx}\frac{\partial T}{\partial x}\mid_{x=L}\\ h_b\left(T\mid_{x=0}-T_a(t)\right)&=k_{xx}\frac{\partial T}{\partial x}\mid_{x=0}\end{aligned} ht(Ta(t)−T∣x=L)hb(T∣x=0−Ta(t))=kxx∂x∂T∣x=L=kxx∂x∂T∣x=0
其中 h t h_t ht 和 h b h_b hb 分别指顶部和底部 HTC 值。结果表明,高压釜内的 HTC 值是高压釜空气温度和压力的重要函数。高压灭菌器中存在各种尺寸和复杂几何形状的多个零件和工具,引入了复杂的气流模式,导致空气温度出现相当大的局部变化,从而导致不同的 HTC 值。这使得复合材料零件本来就很复杂的热化学分析变得更加复杂,因为它需要对具有不同 HTC 值的不同位置的零件热分布进行单独评估。
为了训练 PINN 一维复合材料零件的固化过程,使用以下损失函数:
L ( θ ) = λ i c T L i c T ( θ ) + λ i c α L i c α ( θ ) + λ b c t L b c t ( θ ) + λ b c b L b c b ( θ ) + λ r T L r T ( θ ) + λ r α L r α ( θ ) \mathcal{L}\left(\theta\right)=\lambda_{ic_T}\mathcal{L}_{ic_T}\left(\theta\right)+\lambda_{ic_\alpha}\mathcal{L}_{ic_\alpha}\left(\theta\right)+\lambda_{bc_t}\mathcal{L}_{bc_t}\left(\theta\right)+\lambda_{bc_b}\mathcal{L}_{bc_b}\left(\theta\right)+\lambda_{r_T}\mathcal{L}_{r_T}\left(\theta\right)+\lambda_{r_\alpha}\mathcal{L}_{r_\alpha}\left(\theta\right) L(θ)=λicTLicT(θ)+λicαLicα(θ)+λbctLbct(θ)+λbcbLbcb(θ)+λrTLrT(θ)+λrαLrα(θ)
其中:
L r T ( θ ) = 1 N r ∑ i = 1 N r ∣ ρ C p ∂ T ∂ t ( t r i , x r i ) − k x x ∂ 2 T ∂ x 2 ( t r i , x r i ) − ( 1 − v f ) ρ r H R d α d t ( t r i , x r i ) ∣ 2 L r α ( θ ) = 1 N r ∑ i = 1 N r ∣ d α d t ( t r i , x r i ) − K α m ( 1 − α ) n 1 + e C { α − ( α C 0 + α C T T ) } ( t r i , x r i ) ∣ 2 L b c t ( θ ) = 1 N b c t ∑ i = 1 N b c t ∣ h t ( T a ( t b c t i ) − T ( t b c t i , x b c t i ) ) − k x x ∂ T ∂ x ( t b c t i , x b c t i ) ∣ 2 L b c b ( θ ) = 1 N b c b ∑ i = 1 N b c b ∣ h b ( T ( t b c b i , x b c b i ) − T a ( t b c b i ) ) − k x x ∂ T ∂ x ( t b c b i , x b c b i ) ∣ 2 \begin{gathered} \mathcal{L}_{r_{T}}(\theta) =\frac1{N_r}\sum_{i=1}^{N_r}\left|\rho C_p\frac{\partial T}{\partial t}\left(t_r^i,\mathbf{x}_r^i\right)-k_{xx}\frac{\partial^2T}{\partial x^2}\left(t_r^i,\mathbf{x}_r^i\right)-\left(1-v_f\right)\rho_rH_R\frac{d\alpha}{dt}\left(t_r^i,\mathbf{x}_r^i\right)\right|^2 \\ \mathcal{L}_{r_{\alpha}}\left(\theta\right)=\frac1{N_{r}}\sum_{i=1}^{N_{r}}\left|\frac{d\alpha}{dt}\left(t_{r}^{i},\mathrm{x}_{r}^{i}\right)-\frac{K\alpha^{m}(1-\alpha)^{n}}{1+e^{C\{\alpha-(\alpha_{C0}+\alpha_{CT}T)\}}}\left(t_{r}^{i},\mathrm{x}_{r}^{i}\right)\right|^{2} \\ \mathcal{L}_{bc_t}\left(\theta\right)=\frac1{N_{bc_t}}\sum_{i=1}^{N_{bc_t}}\left|h_t\left(T_a(t_{bc_t}^i)-T\left(t_{bc_t}^i,\mathbf{x}_{bc_t}^i\right)\right)-k_{xx}\frac{\partial T}{\partial x}\left(t_{bc_t}^i,\mathbf{x}_{bc_t}^i\right)\right|^2 \\ \mathcal{L}_{bc_b}\left(\theta\right)=\frac1{N_{bc_b}}\sum_{i=1}^{N_{bc_b}}\left|h_b\left(T\left(t_{bc_b}^i,\mathbf{x}_{bc_b}^i\right)-T_a(t_{bc_b}^i)\right)-k_{xx}\frac{\partial T}{\partial x}\left(t_{bc_b}^i,\mathbf{x}_{bc_b}^i\right)\right|^2 \end{gathered} LrT(θ)=Nr1i=1∑Nr ρCp∂t∂T(tri,xri)−kxx∂x2∂2T(tri,xri)−(1−vf)ρrHRdtdα(tri,xri) 2Lrα(θ)=Nr1i=1∑Nr dtdα(tri,xri)−1+eC{α−(αC0+αCTT)}Kαm(1−α)n(tri,xri) 2Lbct(θ)=Nbct1i=1∑Nbct ht(Ta(tbcti)−T(tbcti,xbcti))−kxx∂x∂T(tbcti,xbcti) 2Lbcb(θ)=Nbcb1i=1∑Nbcb hb(T(tbcbi,xbcbi)−Ta(tbcbi))−kxx∂x∂T(tbcbi,xbcbi) 2
其中下标 T 、 α 、 t T 、 \alpha 、 t T、α、t 和 b b b 表示温度、DoC、顶部和底部损耗分量
PINN、TM以及bc-PINN对比
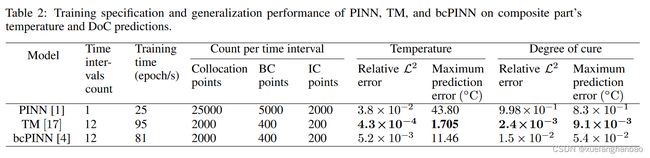
考虑了三种训练场景。首先,使用 PINN 的原始公式来建立基准性能。接下来,实现了两种顺序学习方法,即 TM 和 bcPINN,以解决传统 PINN 的不足。对于这两种方法,时域最初被分为 10 个时间段,并且使用 前文描述的方法自适应更新段长度和计数。最终结果拥有 12 个间隔,其中两个附加间隔出现在 DoC 急剧过渡周围。下表总结了模型的训练规范及其预测性能。
上图分别为PINN、TM以及bc-PINN对温度的预测结果和误差。
上图分别为PINN、TM以及bc-PINN对DoC的预测结果和误差。
可以看到,TM的效果最好,因此作者在接下来的实验中选择TM方法作为SMT框架的一部分。
评估顺序元迁移学习的快速任务适应
通过改变顶部和底部 HTC 并固定其余的工艺设置变量,考虑对 1D 复合材料零件固化中的 20 个相关任务(支持集)进行培训。每个训练任务都是通过从训练分布 [40, 120] W m 2 k \frac{W} {m^2k} m2kW 中随机采样顶部和底部 HTC 来获得。
接下来,SMT 的元学习器在整个分解的时域中进行训练。经过训练后,学习到的参数将用作最佳初始状态,以快速且数据高效地适应具有不同边界规格(即 HTC)的新固化工艺。
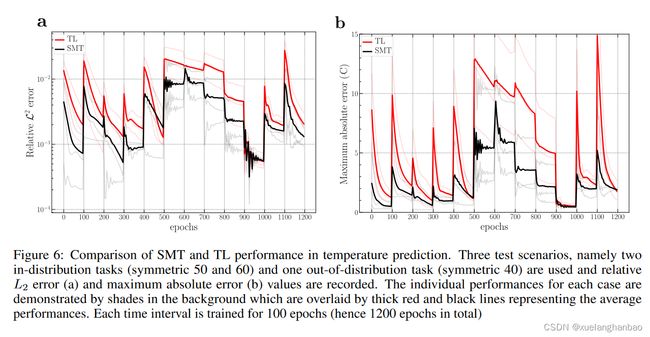
为了评估 SMT,将其泛化性能分别与 MTL 和 TL 方法进行比较。对于 MTL,选择具有三组不同 HTC 值([顶部 HTC-底部 HTC])的三个任务进行学习([60-20] W m 2 k \frac{W} {m^2k} m2kW 、[120-70] W m 2 k \frac{W} {m^2k} m2kW 、[80-40] W m 2 k \frac{W} {m^2k} m2kW)。为了训练 MTL,使用输出层有 6 个神经元的网络(每个任务有两个神经元用于预测温度和 DoC)。这个想法是,使用单个网络对相关任务进行训练可以鼓励学习具有更通用的解决方案空间表示的隐藏状态,从而有助于以更快、更有效的方式在其他类似任务上训练网络。为了训练一个新任务(例如,一组新的 HTC 值),只有输出层被简化为两个神经元层(即,使用一个训练任务的权重进行初始化),而网络的其余部分(隐藏层)保持冻结状态。然后根据新任务的损失分量对网络进行微调。对于 TL,源网络在顶部和底部 HTC 分别设置为 120 W m 2 k \frac{W} {m^2k} m2kW 和 70 W m 2 k \frac{W} {m^2k} m2kW 的固化过程上进行训练,然后用于初始化目标网络以学习文本固化过程。表 3 总结了上述模型针对对称(相同的顶部和底部值)HTC 为 50 W m 2 k \frac{W} {m^2k} m2kW 的测试任务的预测性能(相对 L2 误差)。每个时间间隔使用 200 个搭配、40 个边界点和 20 个初始点,对模型进行 1、100 和 1000 次迭代的微调。
总结
本文提出了一种新的顺序元迁移学习方法。同时通过自适应时间分割将输入域分解为更小的时间段,从而更容易解决偏微分方程问题。然后使用一组子网络在所有时间间隔内按顺序训练 PINN 模型。另一方面,学习框架利用元迁移学习的功能来快速有效地适应新任务,为后续时间段的训练提供了更好的初始参数。
自适应时间分割之前好像没见过,感觉挺有意思的。迁移学习的部分感觉需要特定的问题才行吧,不是很感兴趣。
相关链接:
- 原文:[2308.06447] A Sequential Meta-Transfer (SMT) Learning to Combat Complexities of Physics-Informed Neural Networks: Application to Composites Autoclave Processing (arxiv.org)
- 原文代码:miladramzy/SequentialMetaTransferPINNs: This repository presents a JAX implementation of the paper entitled “Meta-Transfer Sequential Learning of Physics-Informed Neural Networks in Advanced Composites Manufacturing”. The proposed framework integrates a sequential learning strategy with the meta-transfer learning approach to make the training of PINNs in highly nonlinear systems (github.com)