步进电机基础（2.4）- HB型步进电机的转子齿数与主极数之间的关系

前言

基本信息

名称	描述说明
教材名称	步进电机应用技术
作者	坂本正文
译者	王自强

公式

θs = 180° /P*Nr                公式（2. 1)
步进电机的步距角θs，其中Nr 为转子极对数，P为定子相数

θs = ± [ (360°/mP) - (360°n/Nr) ]       公式（2. 2)

Nt =m (nP±1/2)       公式（2. 3)
此为相内磁路时，转子齿Nr 与相数P、主极数m的表达式。式（2. 3)中Nr 必为整数，否则没有意义。此时要注意m必须为偶数。

前言说明

根据我读的《步进电机应用技术》这本书，进行的学习过程中的知识记录和心得体会的记录。

HB型步进电机的转子齿数与主极数之间的关系

  到现在已经学习了步进电机的工作原理、结构，读者一定关心步进电机的相数、转子齿数与主极数之间有什么关系。设计步进电机时肯定要了解这些关系。对于使用步进电机的客户，更重要的是详细了解步进电机的结构和性能。本节将介绍其一般的关系式。

1. HB步进电机的相数、转子齿数、主极数之间的表达式

  如 HB型步进电机为P相，转子齿数Nr , 则依据式（2. 1) 可知其步距角0, 为
   θs=180°/PNr
此时，定子1相主极数（AA相的总和）为m个，均匀配置，其内径配的多个细齿齿数相同。转子永久磁铁产生磁通的磁路如图2. 27 (a) 中的虚线所示，在AA 间形成闭合磁路。与后面叙述的三相HB和五相 HB型等奇数相不完全相同，在AA间不能形成闭合磁路，需要跨接到B相、C相等其他相形成闭合磁路。前者被称为相内磁路式，后者称为相间磁路式。
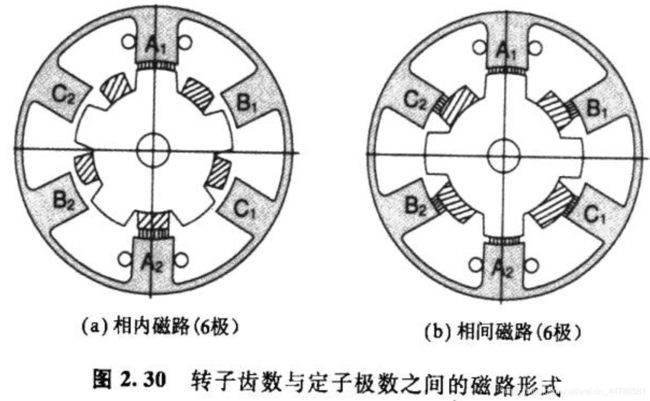
  两相 HB型步进电机皆为相内磁路，而三相 HB型步进电机存在相内磁路和相间磁路两种形式。图2. 30为三相HB型步进电机，有6个磁极，极上并没有小齿，转子齿数也少，图2. 30描述了定子和转子的磁通路径，其中（a) 为相内磁路， (b) 为相间磁路。
  例如图2. 30 (a) 相内磁路的情况，定子主极A1与相邻B相的B1或C相的C2, 向下一相激磁时，会对与A1同极性的转子齿产生吸引力。在永久磁铁后侧的五个转子齿用剖面线表示，其与前侧的转子齿极性相反。同样图2. 30 (b) 为相间磁路，定子主极A1与相邻 B相的B1 或C相的C2, 向下一相激磁时，会对与A1 异性的转子齿产生吸引力。永久磁铁后侧的四个转子齿用剖面线表示，与前侧转子齿极性相反，与（a) 磁路相同。

2. 相内磁路的一般表达式

  图 2.31 (a) 为相内磁路，主磁极北有mP个，由于节距相等，相邻相市A相和B相之间的节距①为360°/mP 当A相通激磁电流时，其磁极与转子极性相反的齿相对应，当再给B相通电，并在B磁极上产生与A 相相问的极性时，转子齿转动到B相上 为简化起见，图中A、B相定子齿由多齿简化为单齿。

此时，与A相相对的转子齿与B相其次要相对的转子齿的节距②如图所示为360°n/N, (n为整数），则步距角为①与②之差：
θs = ± [ (360°/mP) - (360°n/Nr) ]       公式（2. 2)
  将式（2. 1) 代入式（2. 2) 得：
Nt =m (nP±1/2)       公式（2. 3)
  此为相内磁路时，转子齿Nr 与相数P、主极数m的表达式。式（2. 3)中Nr 必为整数，否则没有意义。此时要注意m必须为偶数。
  两相HB型步进电机，当P=2时，主极为8 (m=4) 代入式（2. 3) , 得
Nr = 8n±2       公式（2. 4)
  此为两相HB型步进电机的关系式。两相 HB型步进电机的步距角为通常的1. 8°, 将n=6代入式（2. 4) , 得Nr =50.
  两相HB型步进电机主极为8, 转子齿为50个的结构如图2. 32所示。

  图2. 32 两相HB型步进电机（8主极、50齿、1. 8°) 的结构两相HB型步进电机的步距角为0. 9°, 主极为16,m=8,n=6, 得转子齿为100个的结构如图2. 33所示。

  两相3. 6°步进电机主极为4 (在定转子间会产生不平衡电磁力，所以不鼓励使用此结构）时，依式（2. 3) , 当 P=2,m=2,n=6时，得Nr =25。图2. 34为两相，4 主极，3. 6°的步进电机结构，其外形为42mm步进电机，用于5寸48TPI的FDD (软盘驱动器）上。当为三相时，由式（2. 3) ,m= 4, =4, P=3, 得Nr =50.主极数为mP=12，θs 为1. 2°(如图7. 1、图］7.3、图7. 5、图8. 11、图8. 20、图8. 21所示）。

3. 相间磁路的一般形式

  图2. 31 (b) 为相间磁路，定子节距相等，主极数合计为mP个，相邻A相和B相之间的节距①与相内磁路节距相同，为360°/mP。A 相激磁，与其极性相反的转子齿相对吸引。其次给B相激磁产生与A 相相同的极性，吸引相应的转子齿。为便于理解，将多齿结构简化为单齿结构。
  此时，与A相所对转子齿和B相将相对的转子齿之间的节距②为 360° (n士1/2) /Nr (n整数），如图所示。故步距角为①和②之差：
θs = (-/+) {(360°/mP)-[360°(n±1/2)/Nr]}       公式 （2. 5)
  将式（2. 1) 代入式（2. 5) 得
Nr =m [P (n±1/2) (一／＋）（1/2)]       公式（2. 6)
如相间磁路为三相，令P=3, 则得
Nr =m (3n±1)       公式（2. 7)
三相时，主磁极为3的倍数，最简单的三相3主极时，m=1变成式：
Nr =3n±1       公式（2. 8)
图2. 35为n=3, N, =8的结构图，由式（2. 8) 和式（2. 1) 计算求得， 和θs , 如表2. 3所示。
  设计时要注意，三主极的 HB 型步进电机会产生不平衡电磁力。于只用三个线圈，所以对用于低价电动机的应用场合很有吸引力。
  三相6主极时，m=2, 得下式:
Nr =2 (3n士1)


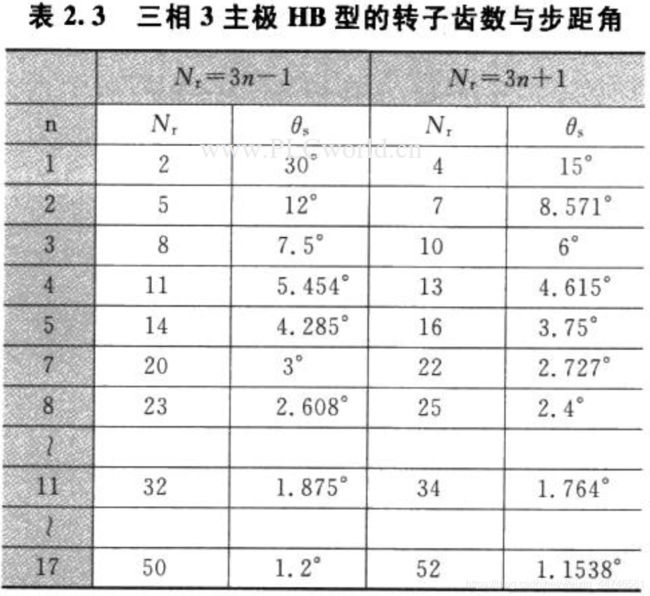
  n=3, N, =16, 步距角3. 75°的电机结构如图2. 36所示。
  三相9主极时，m=3, 则
Nr =3 (3n士1)       公式（2. 10)

  n=7, Nr =60, 步距角1°的电机，轴向剖视如图 2. 37 所示为图 2.32的简化图。
  三相12主极时，m=4, 则
Nr =4 (3n士1)       公式（2. 11)
n=8,Nr=100,步距角0.6°的电机轴向剖视图如图2.38所示。



  上述简要介绍了相内磁路和相间磁路，以及定子主极等节距对称情况下 HB型步进电机的相数、主极数和转子齿数之间的关系表达式。不仅设计电机时要了解这些基本原理，而且使用电机时也要系统了解电机的结构、性能、外形尺寸，并能够依据相数和步距角推出电机内部结构及解决问题的方法。