王道数据结构笔记02-平衡二叉树/平衡树/AVL树
目录
-
- 一、平衡二叉树的定义
- 二、平衡二叉树的插入
-
-
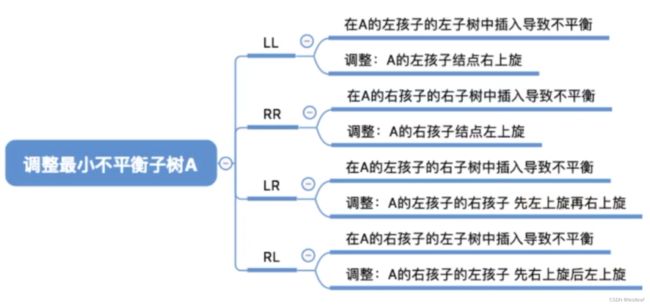
- 1、调整最小不平衡子树(LL):LL平衡旋转(右单旋转)
- 2、调整最小不平衡子树(RR):RR平衡旋转(左单旋转)
- 3、调整最小不平衡子树(LR):LR平衡旋转(先左后右双旋转)
- 4、调整最小不平衡子树(RL):RL平衡旋转(先右后左双旋转)
- 3、平衡二叉树插入操作-练习
-
-
- 【练习1-RR型-左单旋转】
- 【练习2-RL型-先右后左双旋转】
- 【练习3-LR型-先左后右双旋转】
-
-
- 三、平衡二叉树的删除
-
-
- 1、平衡二叉树的插入操作与删除操作的对比分析
- 2、平衡二叉树的删除操作具体步骤
- 3、平衡二叉树删除操作-练习
-
-
- 【练习1-不需要进行后续调整】【重点】
- 【练习2-RR型-需要进行后续调整,最后不平衡不向上传导】【重点】
- 【练习3-RL型-需要进行后续调整,最后不平衡不向上传导】【重点】
- 【练习4-RL型/LR型-需要进行后续调整,最后不平衡向上传导】【难点】
- 【练习5-被删除结点有左右子树-用前驱结点顶替-RR型-需要进行后续调整,最后不平衡不向上传导】【答案不唯一】
- 【练习6-被删除结点有左右子树-用后继结点顶替-RR型/RL型-需要进行后续调整,最后不平衡不向上传导】【答案不唯一】
-
-
- 四、查找效率分析
一、平衡二叉树的定义
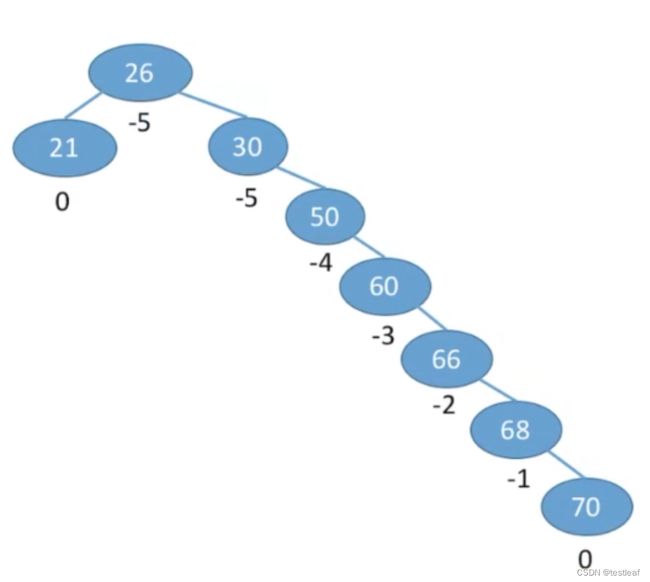
平衡二叉树(Balanced Binary Tree),简称平衡树(AVL树),树上任一结点的左子树和右子树的高度之差不超过1。
简称AVL命名来源于其发明者:G.M.Adelson-Velsky和E.M.Landis,不要和平均查找长度ASL混淆了。
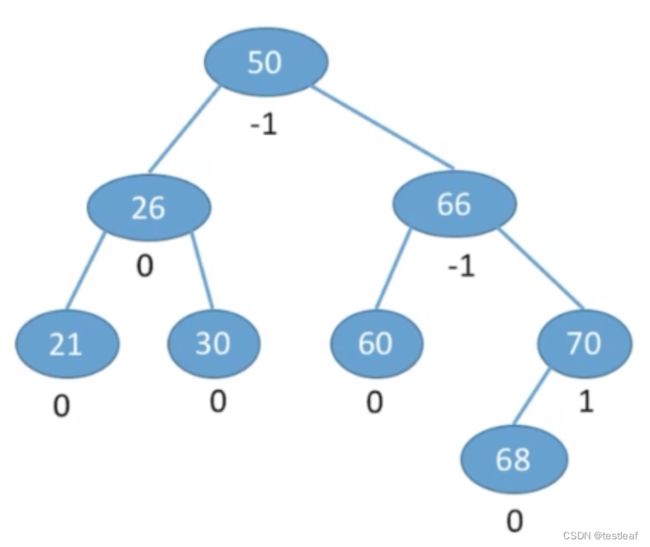
结点的平衡因子=左子树高-右子树高。
平衡二叉树结点的平衡因子的值只可能是-1、0或1。
平衡二叉树结点:
typedef struct AVLNode{
int key; //数据域
int balance; //平衡因子
struct AVLNode *lchild,*rchild;
}AVLNode,*AVLTree;
二、平衡二叉树的插入
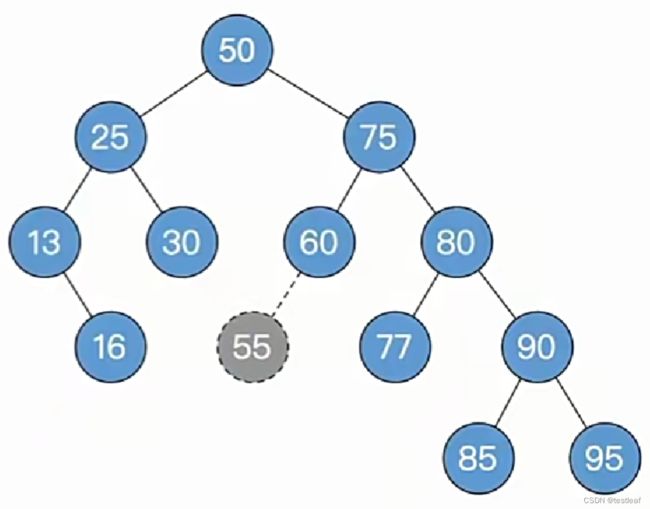
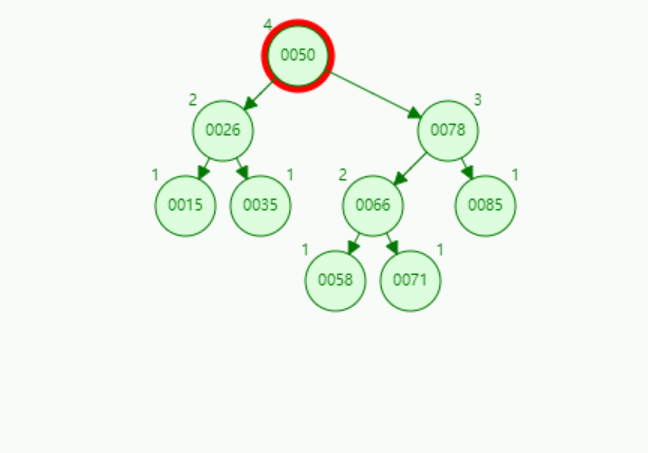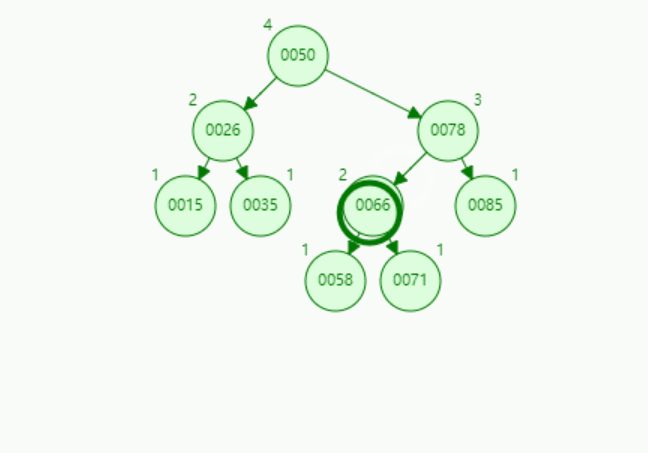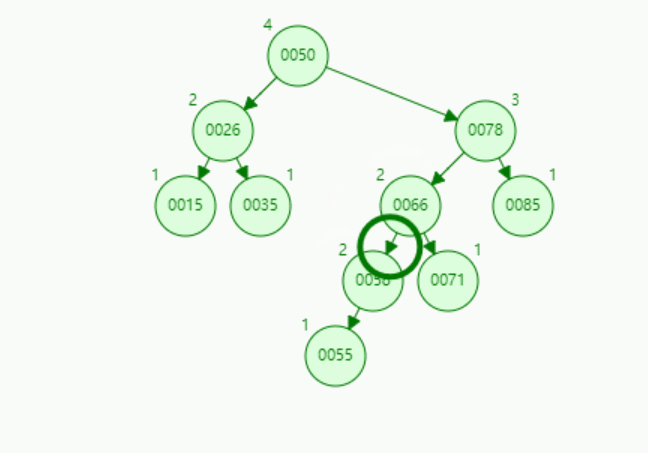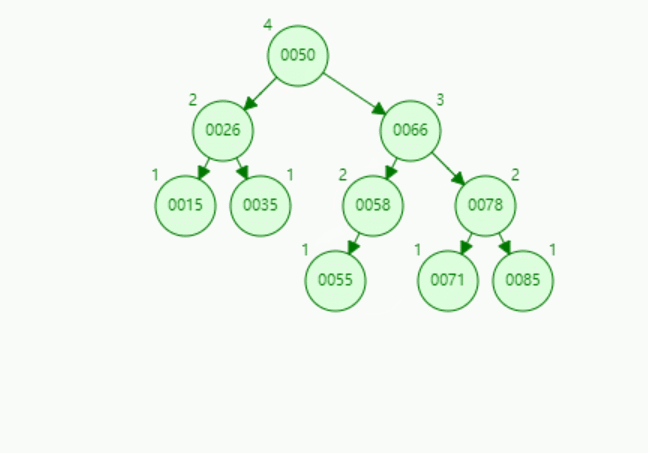
演示1:【LL型-右单旋转】插入关键字为55的结点:
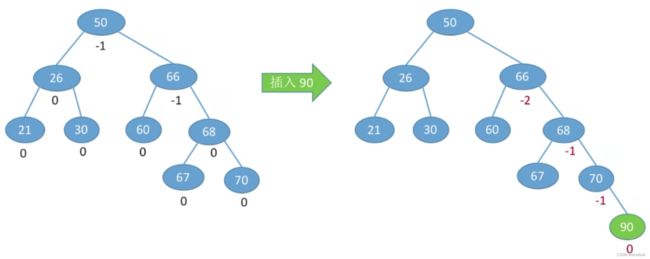
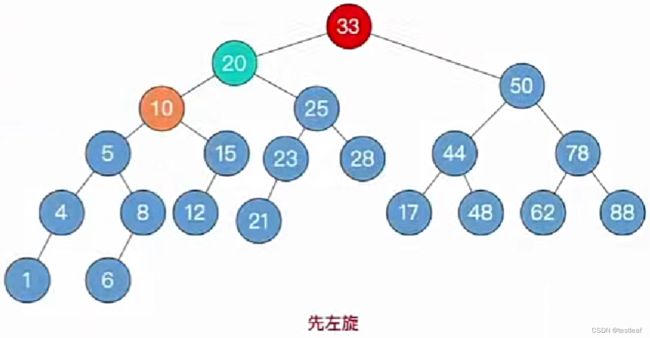
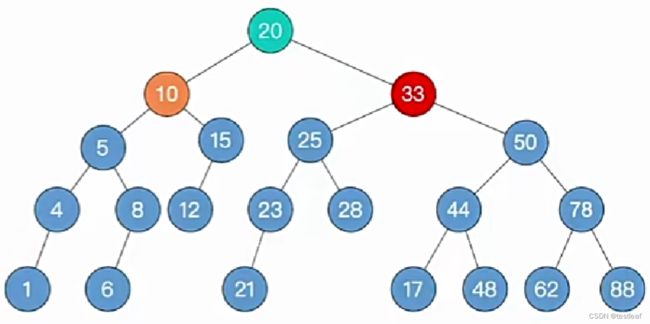
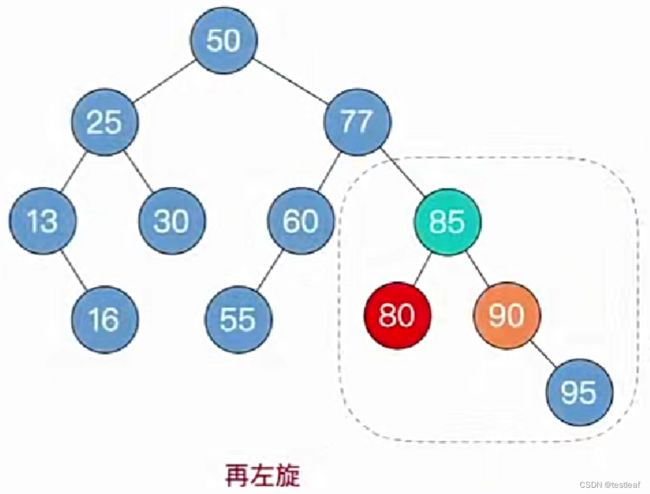
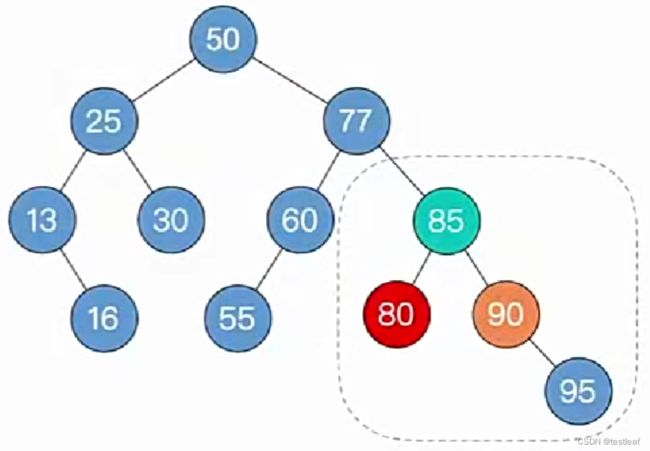
演示2:【RR型-左单旋转】插入关键字为90的结点:

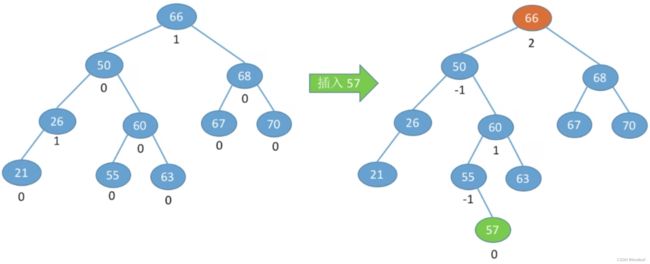
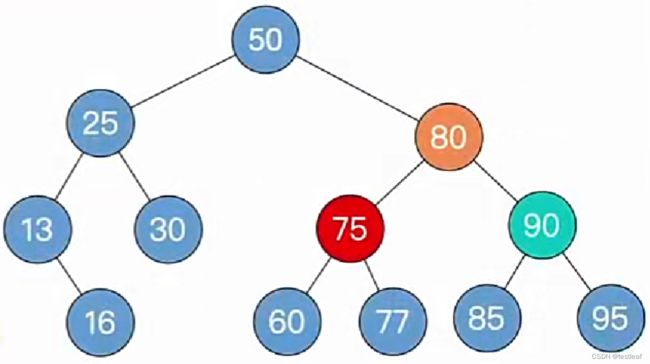
演示3:【LR型-先左后右双旋转】插入关键字为75的结点:

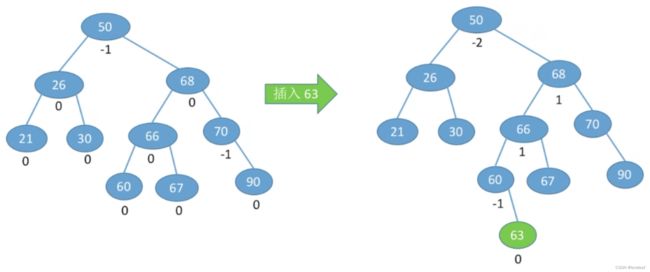
演示4:【RL型-先右后左双旋转】插入关键字为73的结点:
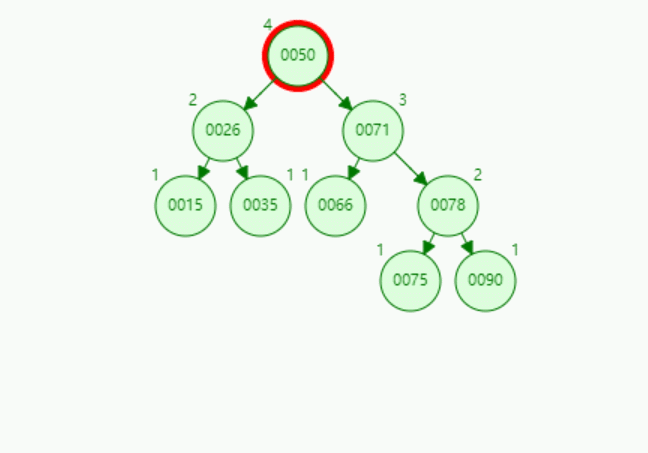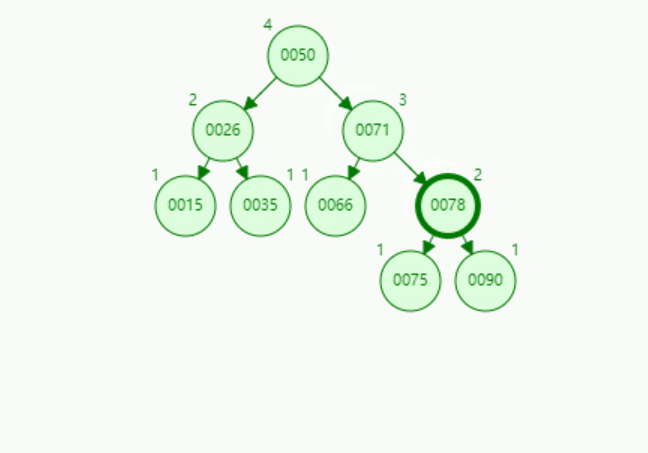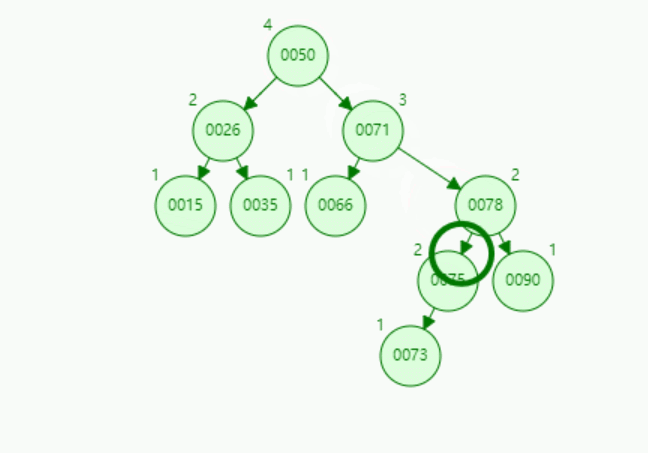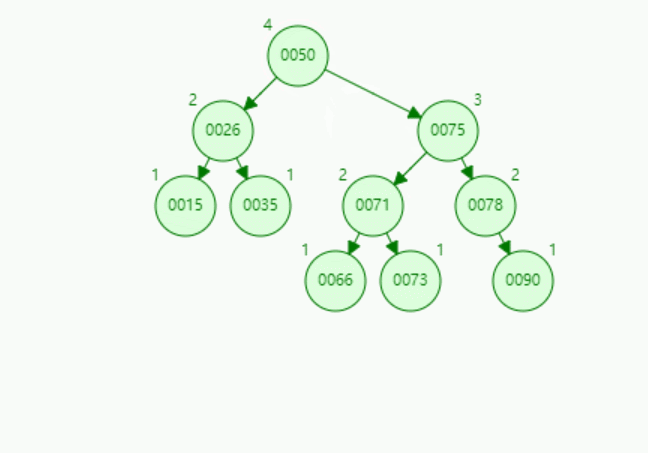
在二叉排序树中插入新结点后,如何保持平衡?
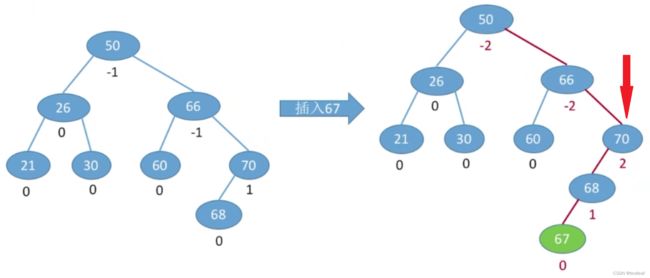
查找路径上的所有结点都有可能受到影响。
解决办法:
从插入点往回找到第一个不平衡结点,调整以该结点为根的子树。
每次调整的对象都是“最小不平衡子树”。

在插入操作中,只要将最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡。
在平衡二叉树中调整最小不平衡子树的目标:
①恢复平衡
②保持二叉排序树的特性:左子树结点值<根结点值<右子树结点值
1、调整最小不平衡子树(LL):LL平衡旋转(右单旋转)
由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。将A的左孩子B结点向右上旋转代替A成为根节点,将A结点向右下旋转成为B的右子树的根节点,而B的原右子树则作为A结点的左子树。

注:
如果最开始,子树BL、BR、AR不满足高度都为H,则无法使A成为当前二叉树的最小不平衡子树。
【LL平衡旋转-右单旋转:代码思路】
实现f向右下旋转,p向右上旋转:
其中f是父亲,p为左孩子,gf为f的父亲;
①f->lchild = p->rchild;
②p->rchild = f;
③gf->lchild/rchild = p;
右旋操作后可以保持二叉排序树的特性:BL

2、调整最小不平衡子树(RR):RR平衡旋转(左单旋转)
由于在结点A的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。将A的右孩子B结点向左上旋转代替A成为根节点,将A结点向左下旋转成为B的左子树的根节点,而B的原左子树则作为A结点的右子树。
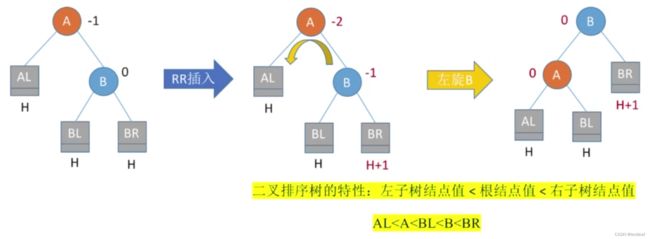
【RR平衡旋转-左单旋转:代码思路】
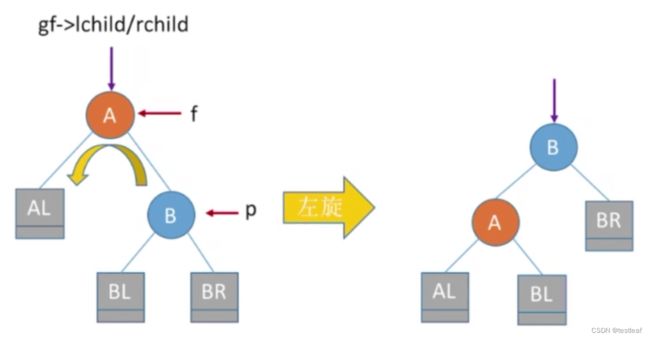
实现f向左下旋转,p向左上旋转:
其中f是父亲,p为左孩子,gf为f的父亲;
①f->rchild = p->lchild;
②p->lchild = f;
③gf->lchild/rchild = p;
左旋操作后可以保持二叉排序树的特性:AL
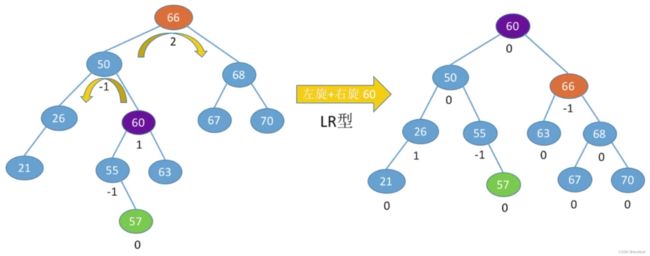
3、调整最小不平衡子树(LR):LR平衡旋转(先左后右双旋转)
由于在A的左孩子(L)的右子树(R)上插入新结点,A的平衡因子由1增至2,导致以A为根的子树失去平衡,需要进行两次旋转操作,先左旋转后右旋转,先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置,然后再把该C结点向右上旋转提升到A结点的位置。
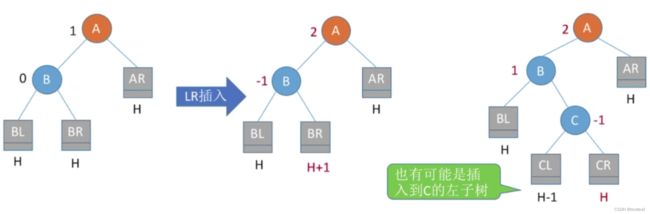
【LR平衡旋转】细节:

其中,C子树的左孩子或右孩子无论是哪个插入了新结点,最后导致最小不平衡子树A不平衡,处理方式都一致:
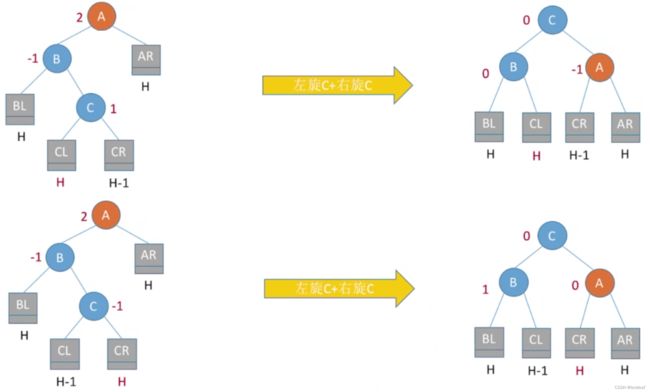
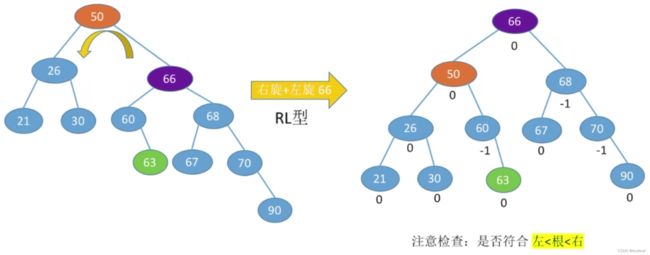
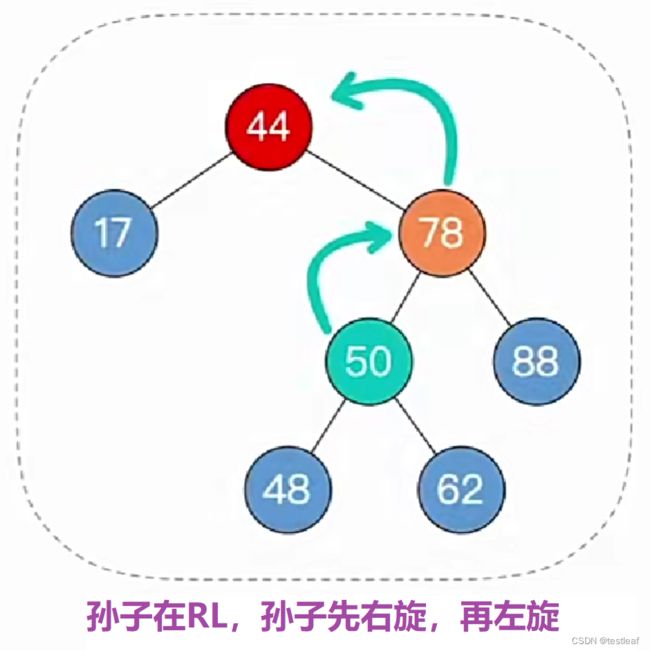
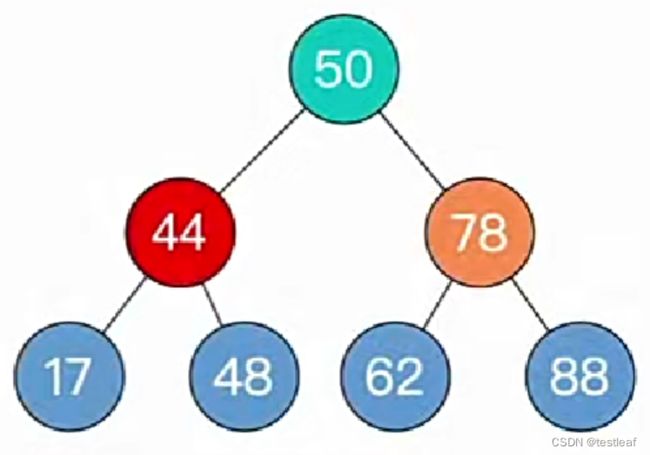
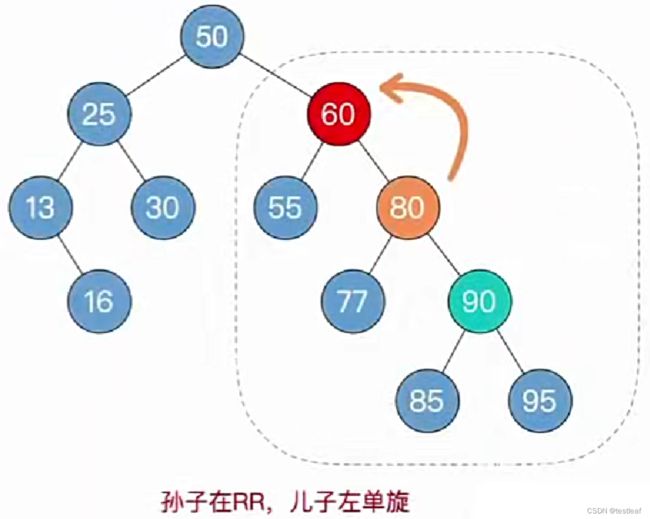
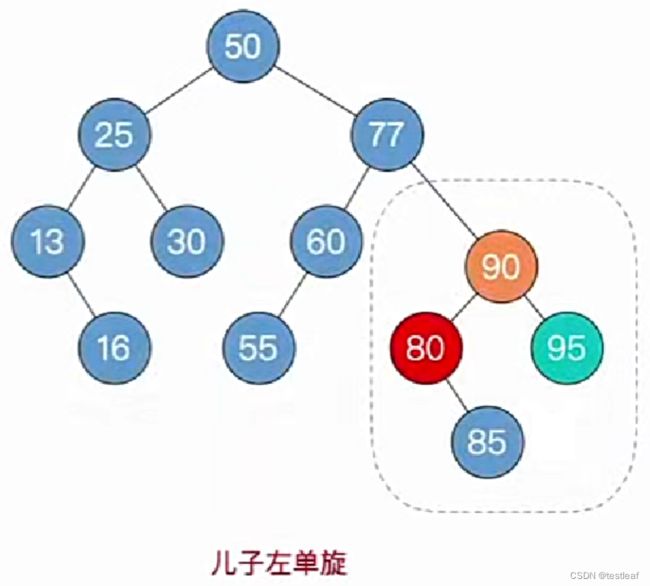
4、调整最小不平衡子树(RL):RL平衡旋转(先右后左双旋转)
由于在A的右孩子(R)的左子树(L)上插入新结点,A的平衡因子由-1减至-2,导致以A为根的子树失去平衡,需要进行两次旋转操作,先右旋转后左旋转。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置,然后再把该C结点向左上旋转提升到A结点的位置。
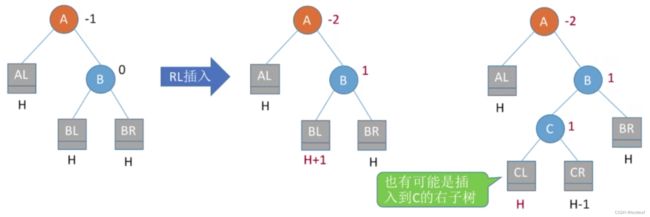
【RL平衡旋转】细节:
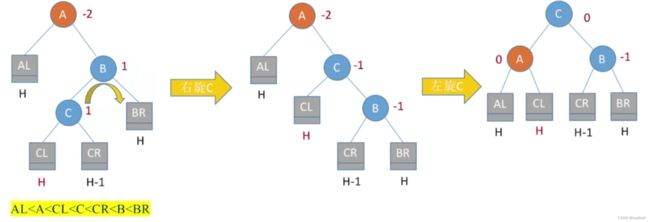
其中,C子树的左孩子或右孩子无论是哪个插入了新结点,最后导致最小不平衡子树A不平衡,处理方式都一致:

【思考】为什么在插入操作中,只要将最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡?
每次调整的对象都是 “最小不平衡子树”
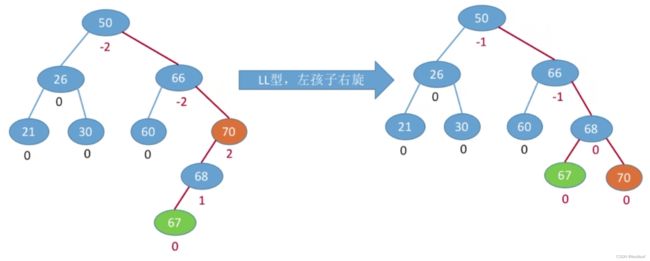
不管是LL型、RR型、LR型、RL型中的哪一种,A子树的树高最开始都为 H + 2 H+2 H+2,插入结点,使A子树的树高增至 H + 3 H+3 H+3,造成了不平衡。通过最小不平衡子树A的平衡调整策略,可以使A子树的树高恢复为 H + 2 H+2 H+2:
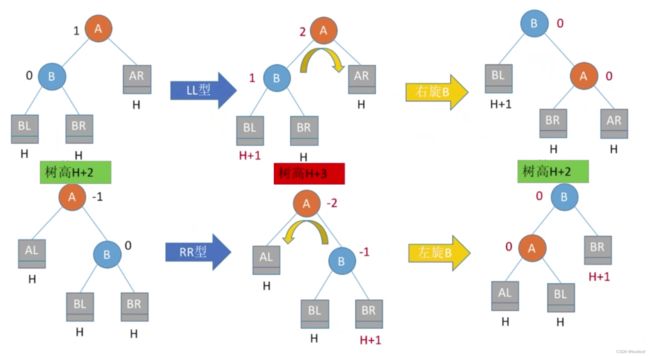
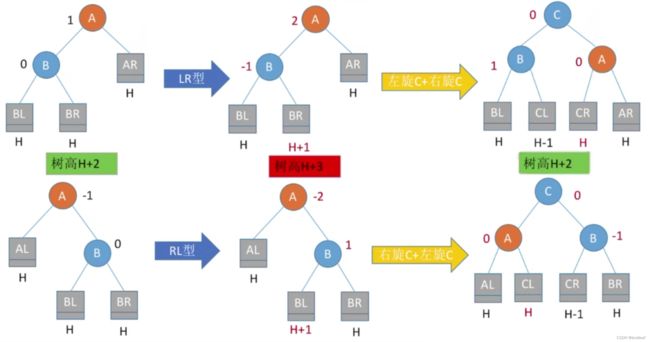
插入操作导致“最小不平衡子树”高度+1,经过调整后高度恢复。那么其父节点及其所有祖先结点的平衡因子就都会恢复成原来的,保持平衡的状态。
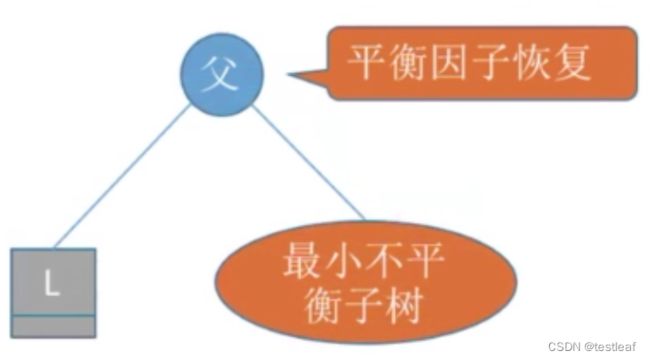
3、平衡二叉树插入操作-练习
注:
进行一系列的调整完成后,注意检查:是否符合左<根<右;
【练习1-RR型-左单旋转】
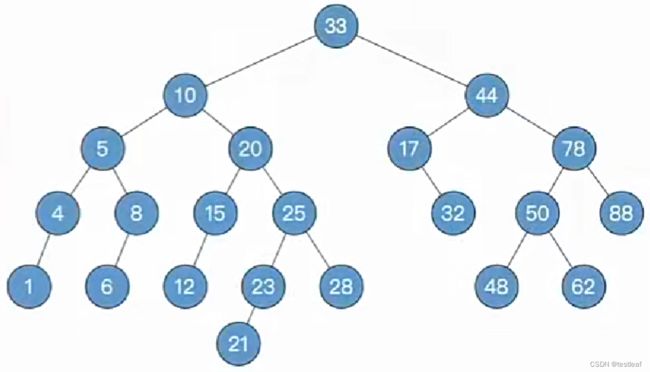
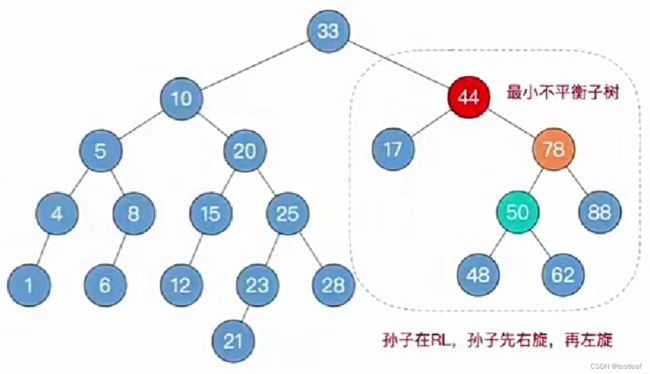
【练习2-RL型-先右后左双旋转】
【练习3-LR型-先左后右双旋转】
三、平衡二叉树的删除
1、平衡二叉树的插入操作与删除操作的对比分析
平衡二叉树的插入操作:
- 插入新结点后,要保持二叉排序树的特性不变(左<中<右);
- 若插入新结点导致不平衡,则需要调整平衡;
平衡二叉树的删除操作:
- 删除结点后,要保持二叉排序树的特性不变(左<中<右);
- 若删除结点导致不平衡,则需要调整平衡;
2、平衡二叉树的删除操作具体步骤
①删除结点(方法同“二叉排序树”);
- 若删除的结点是叶子,直接删;
- 若删除的结点只有一个子树,用子树顶替删除位置;
- 若删除的结点有两棵子树,用前驱(或后继)结点顶替,并转换为对前驱(或后继)结点的删除。
②一路向北找到最小不平衡子树,找不到就完结撒花;
③找最小不平衡子树下,“个头”最高的儿子、孙子;
④根据孙子的位置,调整平衡(LL/RR/LR/RL);
- 孙子在LL:儿子右单旋;
- 孙子在RR:儿子左单旋;
- 孙子在LR:孙子先左旋,再右旋;
- 孙子在RL:孙子先右旋,再左旋;
⑤如果不平衡向上传导,继续②;
- 对最小不平衡子树的旋转可能导致树变矮,从而导致上层祖先不平衡(不平衡向上传递);
平衡二叉树删除操作时间复杂度= O ( l o g 2 n ) O(log_2{n}) O(log2n)
3、平衡二叉树删除操作-练习
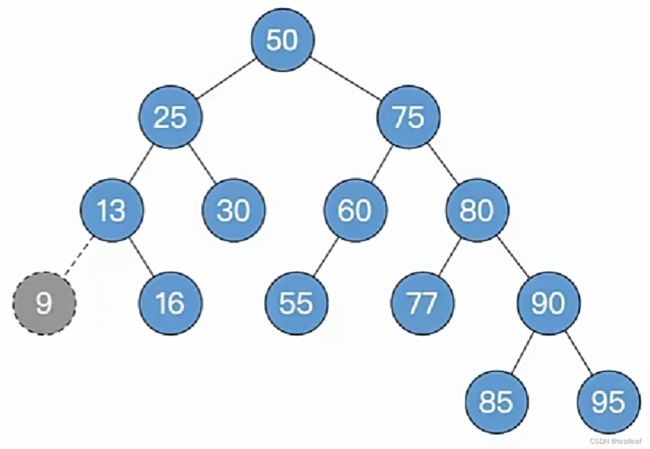
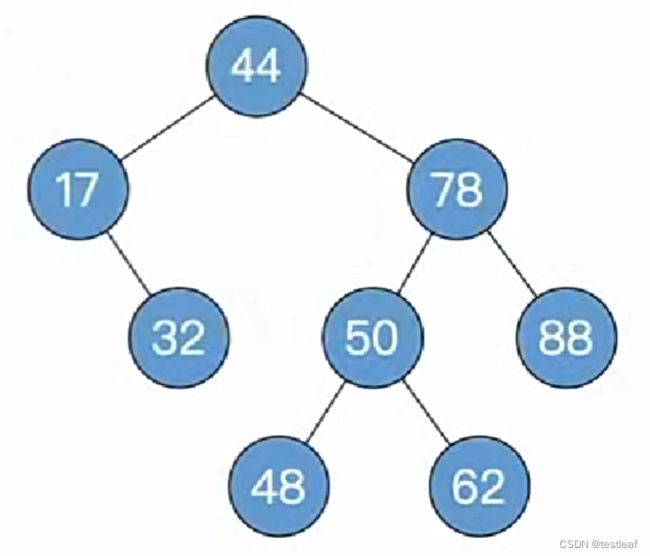
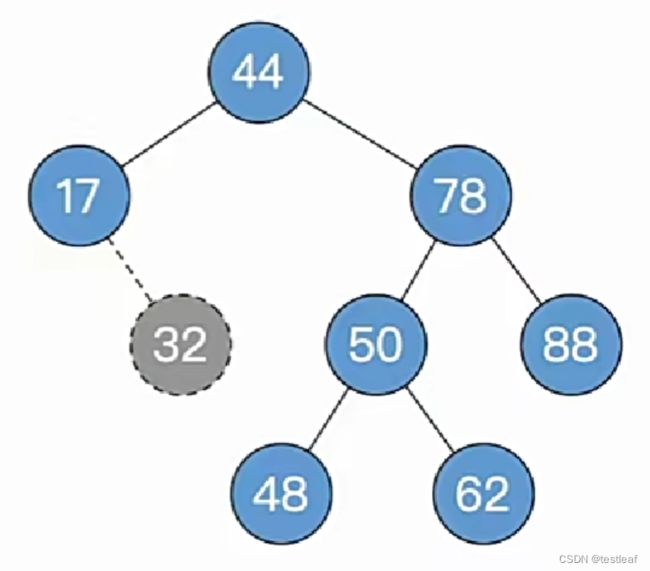
【练习1-不需要进行后续调整】【重点】
删除关键字为9的结点:
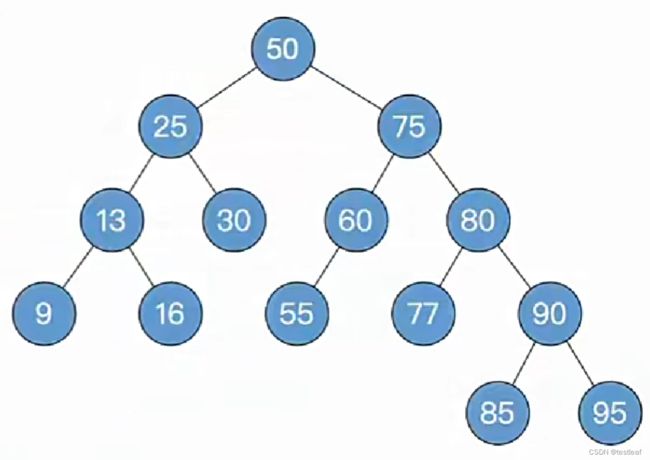
①删除结点(方法同“二叉排序树”);
②一路向北找到最小不平衡子树,找不到就完结撒花;
【练习2-RR型-需要进行后续调整,最后不平衡不向上传导】【重点】
删除关键字为55的结点:
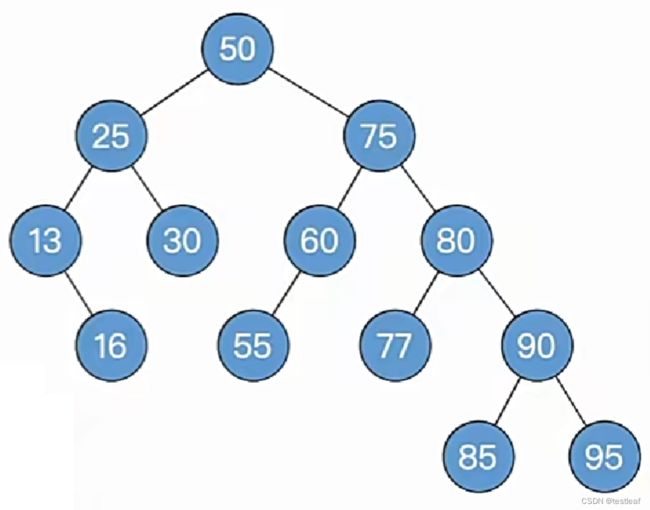
①删除结点(方法同“二叉排序树”);
②一路向北找到最小不平衡子树,找不到就完结撒花;
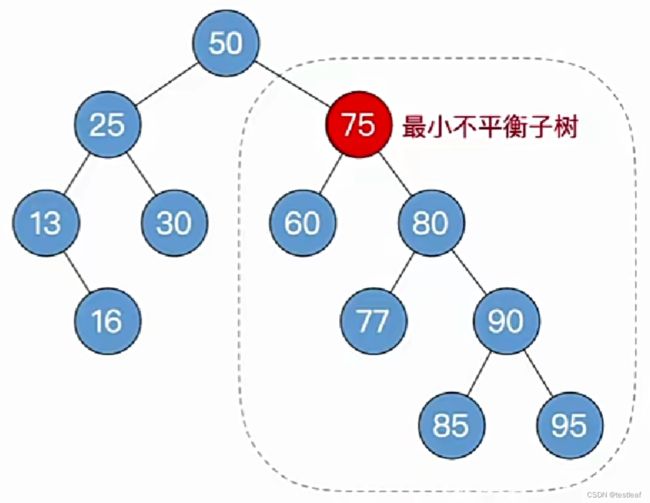
③找最小不平衡子树下,“个头”最高的儿子、孙子;
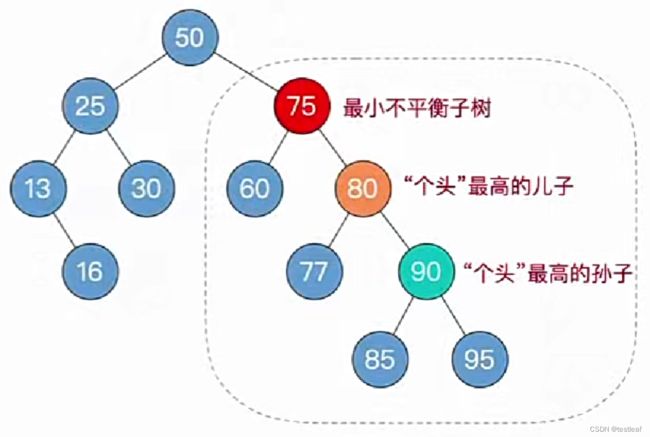
④根据孙子的位置,调整平衡(LL/RR/LR/RL);
⑤如果不平衡向上传导,继续②;
【练习3-RL型-需要进行后续调整,最后不平衡不向上传导】【重点】
①删除结点(方法同“二叉排序树”);
②一路向北找到最小不平衡子树,找不到就完结撒花;
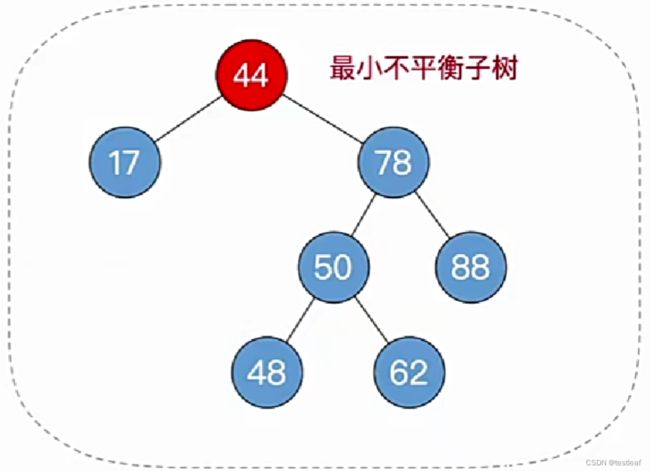
③找最小不平衡子树下,“个头”最高的儿子、孙子;
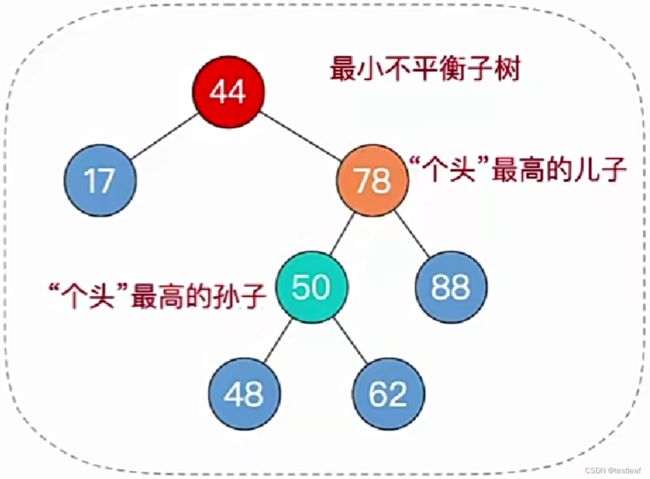
④根据孙子的位置,调整平衡(LL/RR/LR/RL);
⑤如果不平衡向上传导,继续②;
【练习4-RL型/LR型-需要进行后续调整,最后不平衡向上传导】【难点】
①删除结点(方法同“二叉排序树”);
②一路向北找到最小不平衡子树,找不到就完结撒花;
③找最小不平衡子树下,“个头”最高的儿子、孙子;
④根据孙子的位置,调整平衡(LL/RR/LR/RL);
⑤如果不平衡向上传导,继续②;
⟹ \Longrightarrow ⟹由于不平衡向上传导了,继续②
⟹ \Longrightarrow ⟹②一路向北找到最小不平衡子树,找不到就完结撒花;
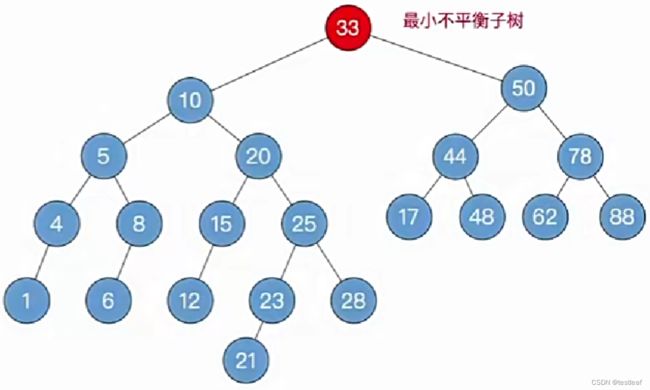
③找最小不平衡子树下,“个头”最高的儿子、孙子;
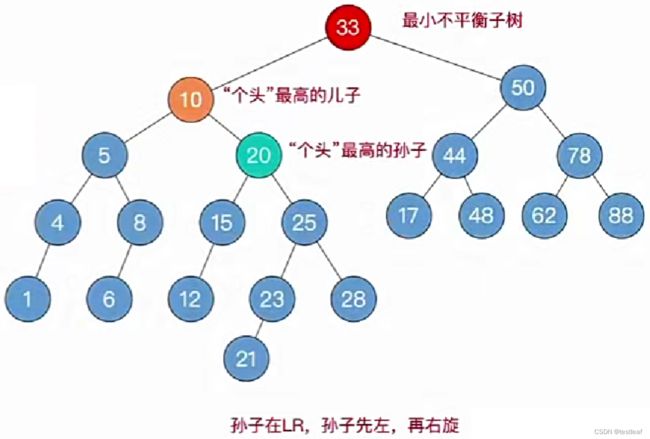
④根据孙子的位置,调整平衡(LL/RR/LR/RL);
⑤如果不平衡向上传导,继续②;
【练习5-被删除结点有左右子树-用前驱结点顶替-RR型-需要进行后续调整,最后不平衡不向上传导】【答案不唯一】
删除关键字为75的结点:
①删除结点(方法同“二叉排序树”);
- 若删除的结点是叶子,直接删;
- 若删除的结点只有一个子树,用子树顶替删除位置;
- 若删除的结点有两棵子树,用前驱(或后继)结点顶替,并转换为对前驱(或后继)结点的删除。
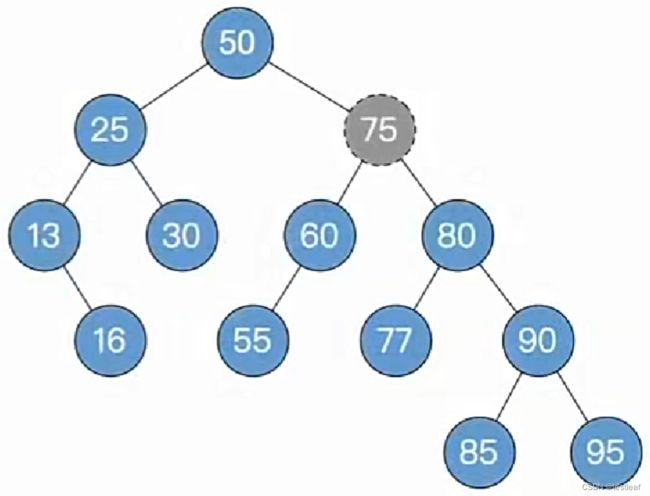
被删除结点有左右子树,用前驱结点顶替(复制数据即可),并转化为对前驱结点的删除:
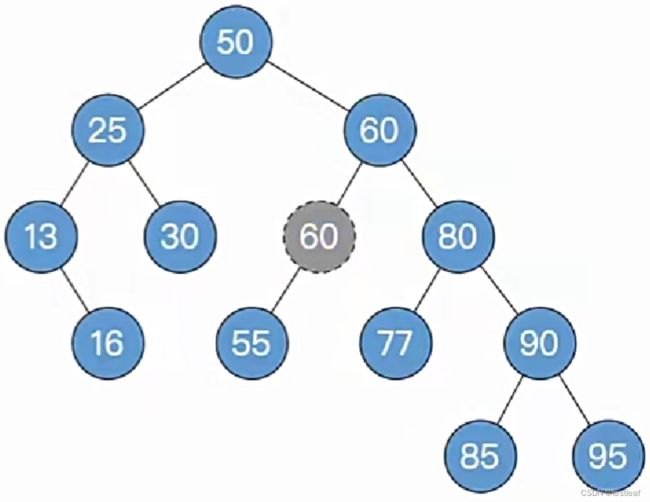
被删除结点只有左子树,用左子树顶替删除位置(用结点实体顶替):
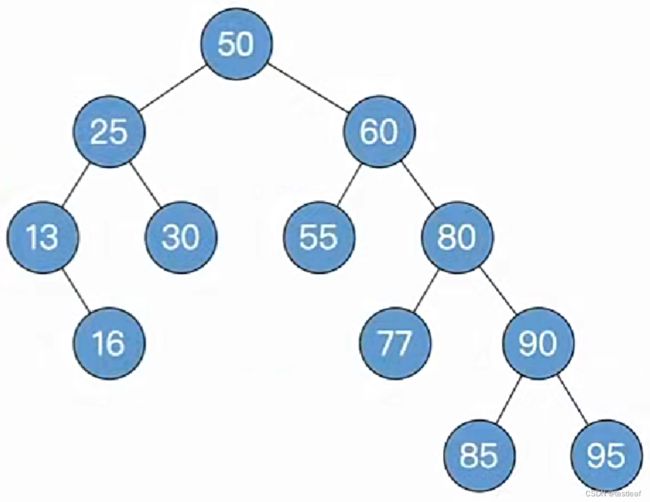
②一路向北找到最小不平衡子树,找不到就完结撒花;

③找最小不平衡子树下,“个头”最高的儿子、孙子;
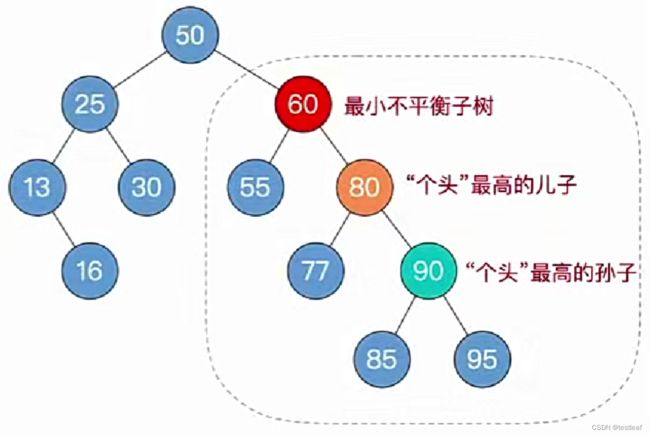
④根据孙子的位置,调整平衡(LL/RR/LR/RL);
⑤如果不平衡向上传导,继续②;
【练习6-被删除结点有左右子树-用后继结点顶替-RR型/RL型-需要进行后续调整,最后不平衡不向上传导】【答案不唯一】
删除关键字为75的结点:
①删除结点(方法同“二叉排序树”);
- 若删除的结点是叶子,直接删;
- 若删除的结点只有一个子树,用子树顶替删除位置;
- 若删除的结点有两棵子树,用前驱(或后继)结点顶替,并转换为对前驱(或后继)结点的删除。
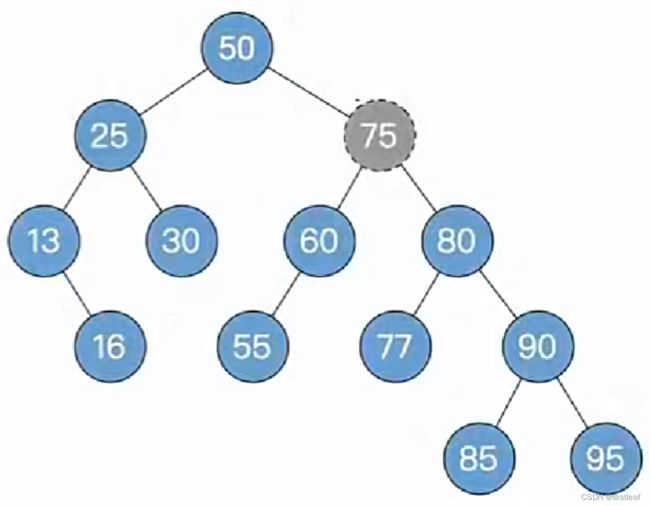
被删除结点有左右子树,用后继结点顶替(复制数据即可),并转化为对后继结点的删除:
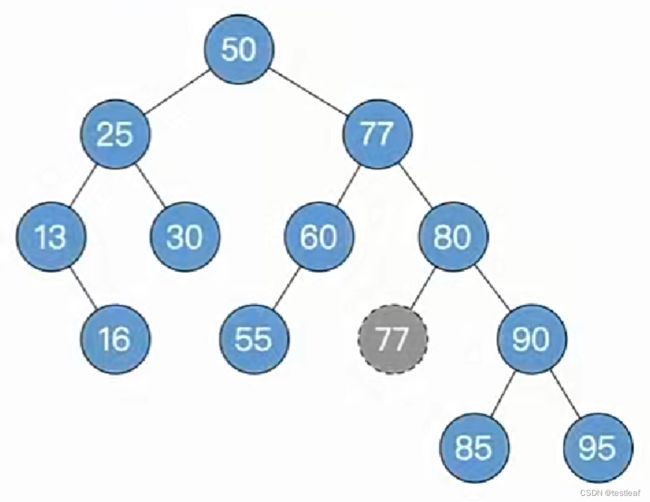
被删除结点为叶子,直接删即可;
②一路向北找到最小不平衡子树,找不到就完结撒花;
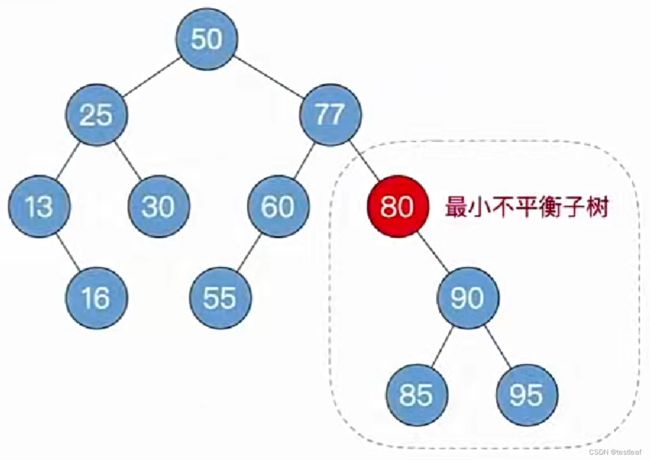
③找最小不平衡子树下,“个头”最高的儿子、孙子;
⟹ \Longrightarrow ⟹选择95作为“个头”最高的孙子:

④根据孙子的位置,调整平衡(LL/RR/LR/RL);
⑤如果不平衡向上传导,继续②;
注:此处在步骤3⃣️也可以选择另一个结点85作为“个头”最高的孙子,如下:
③找最小不平衡子树下,“个头”最高的儿子、孙子;
⟹ \Longrightarrow ⟹选择85作为“个头”最高的孙子:

④根据孙子的位置,调整平衡(LL/RR/LR/RL);
⑤如果不平衡向上传导,继续②;
四、查找效率分析
若树高为 h h h,则最坏情况下,查找一个关键字最多需要对比 h h h次,即查找操作的时间复杂度不可能超过 O ( h ) O(h) O(h);
平衡二叉树:树上任一结点的左子树和右子树的高度之差不超过1。
假设以 n h n_{h} nh表示深度为 h h h的平衡树中含有的最少结点数。
则有 n 0 = 0 n_{0}=0 n0=0, n 1 = 1 n_{1}=1 n1=1, n 2 = 2 n_{2}=2 n2=2,并且有 n h = n h − 1 + n h − 2 + 1 n_{h}=n_{h-1}+n_{h-2}+1 nh=nh−1+nh−2+1;
可以证明含有 n n n个结点的平衡二叉树的最大深度为 O ( l o g 2 n ) O(log_2{n}) O(log2n),平衡二叉树的平均查找长度为 O ( l o g 2 n ) O(log_2{n}) O(log2n);
证明过程见《An algorithm for the organization of information》——G.M.Adelson-Velsky 和E.M.Landis,1962

免责声明:
1.编写此文是为了更好地学习数据结构,如果损害了有关人的利益,请联系删除;
2.如果文中描述欠妥,请在评论中进行指正;
3.文字编写不易,若感觉有用,点赞收藏关注会让博主很开心哦;
4.此外,本文支持任何形式的转载,转载请注明出处,非常感谢!!!
本文源自:https://blog.csdn.net/testleaf/article/details/125956416
参考:
https://www.cs.usfca.edu/~galles/visualization/AVLtree.html