代码随想录Day14 LeetCodeT110平衡二叉树 T257二叉树的所有路径 T404 左叶子之和

 以下思路来自于: 代码随想录 (programmercarl.com)

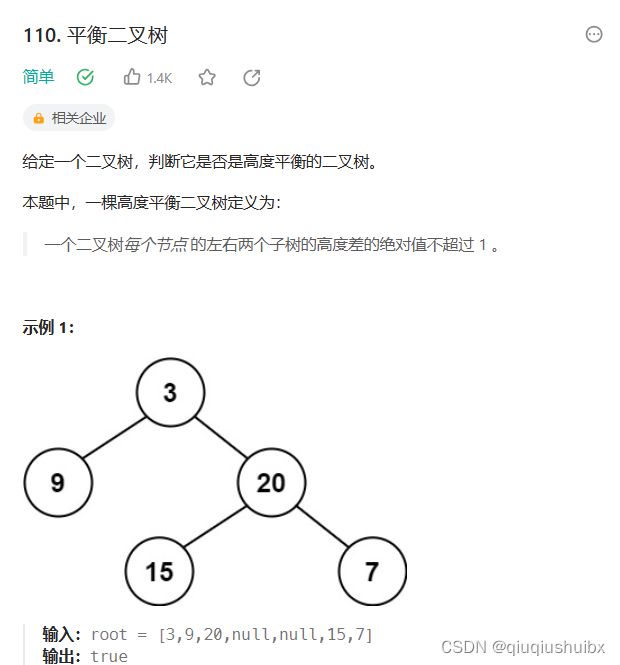
LeetCode T110 平衡二叉树

题目链接:110. 平衡二叉树 - 力扣（LeetCode）

题目思路

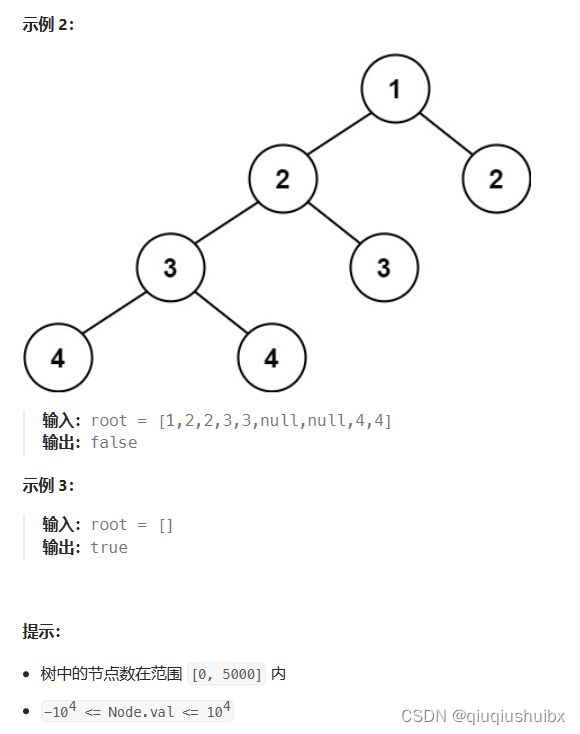
前面我们说过了,求二叉树的深度我们应该使用前序遍历,求二叉树的高度我们应该使用后序遍历,因为后序遍历可以将子树的高度返回给父节点,这样层层递归就能得到答案,而深度是从根节点下去一直到空节点为止,这里清楚了这个逻辑,我们就可以来做这道题了,我们知道一个平衡二叉树的高度差是小于等于1的,而不是平衡二叉树的话只需任意子树的高度大于即可,这里我们仍然使用递归完成

1.确定参数和返回值

求高度,返回值是int 只需传入一个节点即可

int getHeight(TreeNode node)

2.确定终止条件

这里我们遇到空节点处即可返回

if(node == null)
    {
        return 0;
    }

3.确定一次递归逻辑

我们默认如果不是平衡二叉树就返回-1即可,我们按照左右根进行遍历

注:每次获取完左右子树记得判断一次

        int leftHeight = getHeight(node.left);
        if(leftHeight == -1)
        {
            return -1;
        }
        int rightHeight = getHeight(node.right);
        if(rightHeight == -1)
        {
            return -1;
        }
        if(Math.abs(rightHeight-leftHeight)>1)
        {
            return  -1;
        }
        else
        {
            return 1+Math.max(leftHeight,rightHeight);
        }

题目代码

class Solution {
    public boolean isBalanced(TreeNode root) {
        return getHeight(root) != -1;

    }
    int getHeight(TreeNode node)
    {
        if(node == null)
        {
            return 0;
        }
        int leftHeight = getHeight(node.left);
        if(leftHeight == -1)
        {
            return -1;
        }
        int rightHeight = getHeight(node.right);
        if(rightHeight == -1)
        {
            return -1;
        }
        if(Math.abs(rightHeight-leftHeight)>1)
        {
            return  -1;
        }
        else
        {
            return 1+Math.max(leftHeight,rightHeight);
        }
    }
}

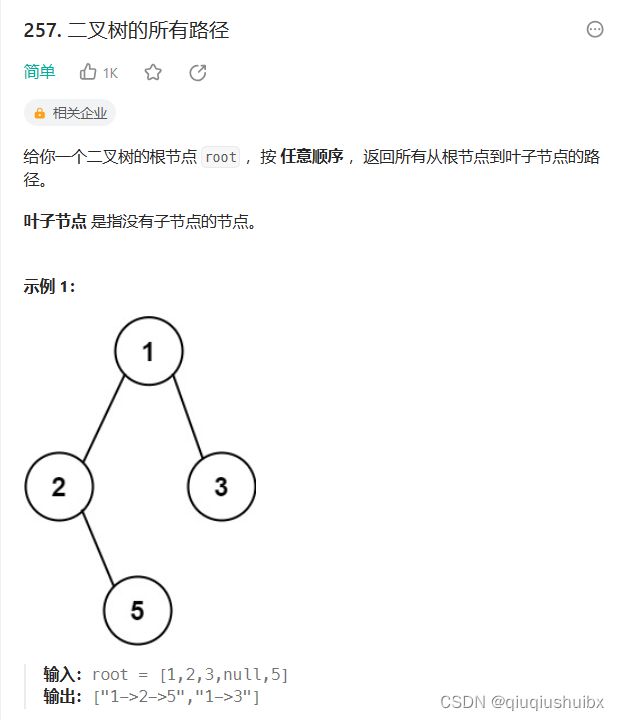
LeetCode T257 二叉树的所有路径

题目链接:257. 二叉树的所有路径 - 力扣（LeetCode）

题目思路

这里我们注意,使用到了回溯算法,其实递归和回溯是相辅相成的,就以上题的示例1为例,我们再记录了125这一条路线的时候还得回去记录13这一条路径,这就用到了回溯.这里千万不要把递归和回溯拆开,因为有一个递归就有一个回溯.

题目代码

class Solution {
    public List binaryTreePaths(TreeNode root) {
        List res = new ArrayList<>();
        if(root == null)
        {
            return null;
        }
        List path = new ArrayList<>();
        travsal(root,path,res);
        return res;

    }
    void travsal(TreeNode node,List path,List res)
    {
        //前序
        path.add(node.val);
        if(node.left == null && node.right == null)
        {
            StringBuilder sb = new StringBuilder();
            for(int i = 0;i");
            }
            sb.append(path.get(path.size()-1));
            res.add(sb.toString());
        }
        if(node.left != null)
        {
        //一次递归一次回溯
            travsal(node.left,path,res);
            path.remove(path.size()-1);

        }
         if(node.right != null)
        {
            travsal(node.right,path,res);
            path.remove(path.size()-1);

        }

    }
}

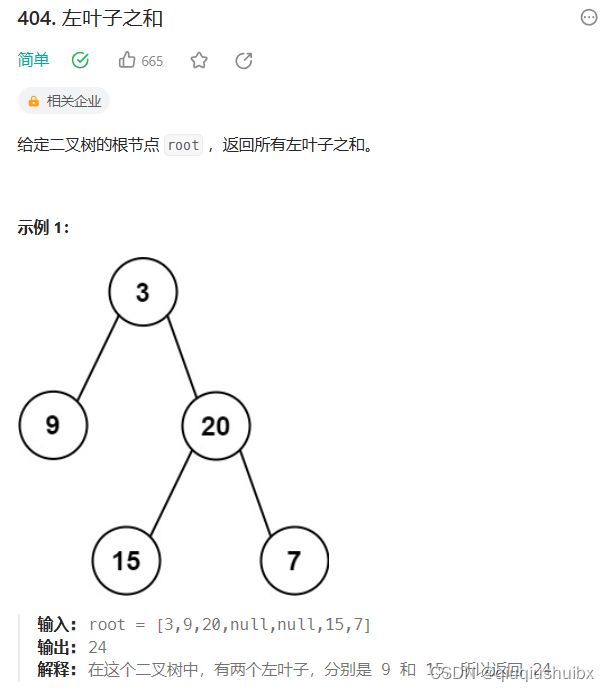
LeetCode T404 左叶子之和

题目链接:力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

题目思路

这里我们注意之前我们只能判断叶子结点,而不能知道左叶子节点,这里我们就可以用过叶子结点的上一个节点知道是否为左叶子节点,这里我们仍然使用递归实现,这里就不需要额外创建新函数(仍然使用后序遍历)

1.函数返回值和参数

public int sumOfLeftLeaves(TreeNode root)

2.终止条件

无论是遇到空节点或者叶子节点都返回0,因为我们不知道该叶子结点是否为我们需要收集的节点

    if(root == null)
        {
            return 0;
        }
    if(root.left == null && root.right == null)
        {
            return 0;
        }

3.单层递归

        //后序
        int leftNum = sumOfLeftLeaves(root.left);
        int rightNum = sumOfLeftLeaves(root.right);
        int sum = 0;
        //中间处理过程
        if(root.left != null && root.left.left == null && root.left.right == null)
        {
            sum = root.left.val;
        }
        sum = sum + leftNum + rightNum;
        return sum;

题目代码

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if(root == null)
        {
            return 0;
        }
        if(root.left == null && root.right == null)
        {
            return 0;
        }
        //后序
        int leftNum = sumOfLeftLeaves(root.left);
        int rightNum = sumOfLeftLeaves(root.right);
        int sum = 0;
        if(root.left != null && root.left.left == null && root.left.right == null)
        {
            sum = root.left.val;
        }
        sum = sum+leftNum+rightNum;
        return sum;
        
        

    }
    
}