【从零开始】二叉树全攻略（02）：递归与回溯

二叉树遍历
二叉树递归入门

上次说了很多用递归可以简单解决的二叉树题目，这次继续用一些题目说明，同时探究一下递归中的回溯现象。

继续用递归解题

由浅及深，先来这道题。

leetcode 617 合并二叉树

给定两个二叉树将它们合并，合并就是互补的过程，如果两棵树的对应位置都有节点，那么就将值相加。

我们可以先合并根节点，再到达子树，也可以反过来。

所以遍历顺序是无关的。

我们拿后序来举例，需要思考的是如果我们已经将根节点的左右子树合并成功，根节点如何操作得到的结果。

当然操作其实也很简单，就是把两个根节点的值相加，然后把合并后的左右子树连到根节点上。

TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(root1==NULL)
            return root2;
        if(root2==NULL)
            return root1;
        
        TreeNode *left=mergeTrees(root1->left,root2->left);
        TreeNode *right=mergeTrees(root1->right,root2->right);

        root1->val+=root2->val;
        root1->left=left;
        root1->right=right;

        return root1;

    }

再来一道

leetcode 404 左叶子之和

给定一个二叉树，返回所有左叶子之和。

左叶子，需要翻译一下，就是左边没有左右子树的叶子节点。

我们使用后序遍历从叶子节点开始，计算左叶子，然后递归将它们相加，就是左叶子之和。

用我们一贯的思路来看，就是在得到左右子树的左叶子之和后，从根节点出发，如何加上根节点的结果。

需要注意的是左叶子的判断，只有符合条件的才可以加入结果。

int sumOfLeftLeaves(TreeNode* root) {
        if(root==NULL)
            return 0;
        int left=sumOfLeftLeaves(root->left);
        int right=sumOfLeftLeaves(root->right);
        int value=0;

        if(root->left&&!root->left->left&&!root->left->right){
            value=root->left->val;
        }
        return value+left+right;

    }

还有一道经典的题目，平衡二叉树

leetcode 110 平衡二叉树

平衡二叉树的概念我们都很熟悉，一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1

这道题要求判断一个数是否为平衡二叉树。

出发点就是先判断子树，再递归到根节点。如果子树左右高度差已经大于1，那么可以直接返回false

但是我们需要高度差是int值，而且需要这个int值来进行递归，所以需要辅助函数。

int getHeight(TreeNode *root){
        if(root==NULL)
            return 0;
        
        int left=getHeight(root->left);
        if(left==-1)return -1;
        int right=getHeight(root->right);
        if(right==-1)return -1;
        int result;

        if(abs(left-right)>1){
            return -1;
        }
        else{
            result=max(left,right)+1;//返回最高的子树高度
        }
        return result;
    }
    bool isBalanced(TreeNode* root) {
        return getHeight(root)==-1?false:true;

    }

再来一道层序遍历中比较常见的题目，我们用递归来解答

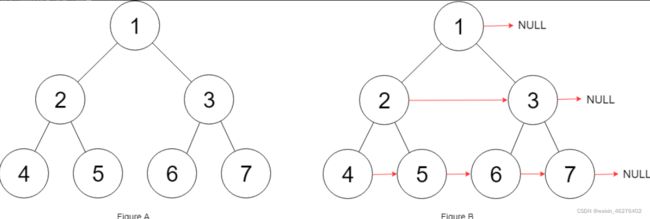
leetcode 116 填充每个节点的下一个右侧节点指针

让每一个next指针都指向下一个右侧节点

可以看出使用层序遍历的话会比较直接，每层连线就可以了。

如果我们使用递归也是可以的，我们去递归子树，让其的左子树和右子树连接。

这里有一个问题，如果这样递归，像图中5，6这样的节点是无法连在一起的。

所以我们需要辅助函数，传入两个节点，让其左右连接。

Node* connect(Node* root) {
        if(root==NULL)
            return NULL;
        traverse(root->left,root->right);
        return root;
        
        
    }

    void traverse(Node* node1,Node* node2){
        if(node1==NULL||node2==NULL){
            return;
        }

        node1->next=node2;//左右节点连接
        traverse(node1->left,node1->right);//node1的左子树和右子树连接
        traverse(node2->left,node2->right);//node2的左子树和右子树连接
        traverse(node1->right,node2->left);//node1的右子树和node2的左子树连接
        
    }

递归与回溯

回溯是一类单独的解题思路，而递归是用来实现的一种方法。回溯的题目后面会单独来说，比如排列组合问题。

而在二叉树中，也有一类题目用到了回溯的思想，那就是–路径。

与路径相关的题目都需要搜索路径，所以需要深搜，也就是搜索到一条路径后，再回退继续搜索。

朴素的写法

先来看一道路径题目

leetcode 257 二叉树的所有路径

返回所有从根节点到叶子节点的路径，并且输出。

这个输出结果有固定的形式：

输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

所以我们需要记录路径的path和返回结果的vector

在遍历时，这两个变量也会随着路径不同而变化，所以我们把它们加入到参数中。

void traverse(TreeNode *root,vector& path,vector& res)

因为从根节点出发，所以是前序遍历，先遍历根节点。

而我们对于根节点的操作就是先将该节点加入path，再判断如果有左子树就遍历左子树，有右子树就遍历右子树。

当到达叶子节点时，说明一条路径已经结束，可以把它加入res。

void traverse(TreeNode *root,vector& path,vector& res){
        path.push_back(root->val);

        
        if(root->left){
            traverse(root->left,path,res);
            path.pop_back();//回溯
            
        }

        if(root->right){
            traverse(root->right,path,res);
            path.pop_back();//回溯
            
        }

        if(root->left==NULL&&root->right==NULL){
            //需要把path里的值转换为固定格式的string
            string rpath;
            for(int i=0;i binaryTreePaths(TreeNode* root) {
        vectorresult;
    	vector path;
        if(root==NULL)return result;
        transfernode(root,path,result);
        return result;

    }

这里我们先存入int类型的path，然后再将值取出转换为要求的path。

传引用与传值

那可不可以不进行转换，直接得到我们想要的path呢？

也是可以的，这里的玄妙就藏在回溯的部分。

我们在递归子树时，当递归结束需要pop来回退一步。

这是因为我们传参时传入了引用，所以原值被修改了，需要手动pop

现在我们把vector改为string，直接加上"->"

 void transfernode(TreeNode *cur,string& path,vector& result){
        path+=to_string(cur->val);
        if(cur->left==NULL && cur->right==NULL){
            result.push_back(path);
            return;
        }

        if(cur->left){
            path+="->";
            transfernode(cur->left,path,result);
            path.pop_back();//数值
            path.pop_back();//>
            path.pop_back();//-
            
        }

         if(cur->right){
            path+="->";
            transfernode(cur->right,path,result);
            path.pop_back();
            path.pop_back();
            path.pop_back();
        }
    }

vector binaryTreePaths(TreeNode* root) {
        vectorresult;
    	string path;
        if(root==NULL)return result;
        transfernode(root);
        return result;

    }

如果能看懂这三个pop_back()，那就说明你理解了回溯的过程。

我们传入path的引用，会修改原值，所以这时候需要回溯时要pop后加入的数值，同时也要把我们加进去的"->"pop出来。

注意这是两个字符，所以要pop两次。

精简做法

在理解了上述做法后，我们可以掌握更加简单的做法，那就是传值。

大家都知道传值是复制操作，不会影响原值。

那我们传入path值，这样在回溯时就不会影响原值了。

如果想让"->“也自动回到上一步而不用手动pop，那就把”->"也加入参数中。

最终可以得到下面的解法：

void transfernode(TreeNode *cur,string path,vector& result){
        path+=to_string(cur->val);
        if(cur->left==NULL && cur->right==NULL){
            result.push_back(path);
            return;
        }

        if(cur->left){
            transfernode(cur->left,path+"->",result);
        }

         if(cur->right){
            transfernode(cur->right,path+"->",result);
        }
    }

注意这里是传值的。

趁热打铁，再来看一道路径题目

leetcode 113 路径总和2

给定一个target，找到从根节点到叶子节点路径总和等于给定目标和的路径

如何定义辅助函数呢？

因为我们要从根节点出发，前序遍历，所以比较好的做法是定义一个count参数，从一开始count=target，在每次递归时用count计算减去当前节点值剩余多少，如果到达叶子节点时count==0，就说明找到了目标和的路径。

同时也需要一个path来存放路径，最后result存放所有结果。

void traverse(TreeNode* root,int count,vector& path,vector>& result){
        if(root->left){
            path.push_back(root->left->val);//放入节点
            count-=root->left->val;//减去相应数值
            traverse(root->left,count,path,result);
            count+=root->left->val;//回溯
            path.pop_back();//回溯
        }

        if(root->right){
            path.push_back(root->right->val);
            count-=root->right->val;
            traverse(root->right,count,path,result);
            count+=root->right->val;//回溯
            path.pop_back();//回溯
        }

        if(root->left==NULL&root->right==NULL&&count==0){//只有刚好相等才存入结果
            result.push_back(path);
            return ;

        }
        else if(root->left==NULL&root->right==NULL)
            return;
    }

vector> pathSum(TreeNode* root, int targetSum) {
        if(root==NULL)
            return result;
   		vectorpath;
    	vector>result;
    //处理根节点
        path.push_back(root->val);
        int count=targetSum-root->val;
        traverse(root,count,path,result);
        return result;

    }

这里根节点不能直接遍历，而是要先存入path，再将相应的数值减去。

回溯的地方也很全面，先回溯count再回溯path。

这就是完整的回溯过程。

我们依旧按照上面的思路来精简，能不能把回溯的部分让参数自动来做？

那就把count和path都放入参数中，并且不使用引用，而是传值。

void traverse(TreeNode* root,int count,vector path){
        path.push_back(root->val);
        if(root->left){
            traverse(root->left,count-root->left->val,path);
        }

        if(root->right){
           
            traverse(root->right,count-root->right->val,path);
           
        }

        if(root->left==NULL&root->right==NULL&&count==0){
            result.push_back(path);
            return ;

        }
        else if(root->left==NULL&root->right==NULL)
            return;
    }

vector> pathSum(TreeNode* root, int targetSum) {
        if(root==NULL)
            return result;
        vectorpath;
        vector>result;
        traverse(root,targetSum-root->val,path);
        return result;

    }

先思考path，这里如果使用引用，那么还需要pop操作。如果传值，则不会改变原值，在退出递归时保持不变。

为什么count也不需要回溯了？

因为已经包含在了参数count-root->left->val中了，这样在退出时也不会改变count的值

体会一下这种方法的巧妙之处。

参数到底有几个？

我们在写辅助函数时，参数里又是path又是result的，那么参数到底多少个合适呢？

其实对于完整的回溯解法，就像上面的将全部回溯情况列出来的解法，参数是可调整的。

就像这个函数

void transfernode(TreeNode *cur,string& path,vector& result)

如果我们将回溯写全，那么path和result其实都有既定的操作，所以在不在参数列表中都无所谓。

void transfernode(TreeNode *cur）

**唯一的区别是在何处定义。**如果写在参数里就可以在主函数里定义，如果不在参数里就需要在全局定义。

而对于我们使用“自动回溯”的函数来说，就不可以随便去掉参数了，除非我们已经将回溯写全了。

当然，result基本在哪里都不会影响结果，比如二叉树的所有路径这道题，精简写法也完全可以去掉result

vectorresult;
    void transfernode(TreeNode *cur,string path){
        path+=to_string(cur->val);
        if(cur->left==NULL && cur->right==NULL){
            result.push_back(path);
            return;
        }

        if(cur->left){
            transfernode(cur->left,path+"->");
        }

         if(cur->right){
            transfernode(cur->right,path+"->");
        }
    }
    vector binaryTreePaths(TreeNode* root) {
        string path;
        
        transfernode(root,path);
        return result;

    }

当然，需要注意result定义的位置。

关于回溯的返回值

前面讨论了几道路径的题目，我们的辅助函数返回值都是void。

但其实返回值是什么，也有一定的学问。

上面的题目有一个共同的特点：返回所有结果，这就意味着需要把所有结果都遍历出来。

而也有一些题目，并不要求返回所有路径，这时候就需要返回值来得到答案。

leetcode 112 路径总和

这道题和上一道路径总和2很类似，也需要找到和为target的路径。

区别在于本题只要判断是否存在这样的路径。并不需要遍历整个数。

我们利用bool返回值直接可以在条件中返回结果。

bool traverse(TreeNode* root,int count){
        if(root->left){
           if( traverse(root->left,count-root->left->val))
                return true;
        }

        if(root->right){
            if(traverse(root->right,count-root->right->val))
                return true;
        }

        if(!root->left&&!root->right&&count==0)
            return true;
        else if(!root->left&!root->right)
            return false;
        
        return false;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root==NULL)
            return false;
        return traverse(root,targetSum-root->val);
    }

掌握了2的写法，1就非常好写。

最后再来看一道题目，我们可以当作上一篇中出现的常规递归题目来看，也可以看作回溯。

leetcode 236 二叉树的最近公共祖先

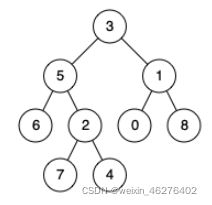
给定一个二叉树，找到两个节点的最近公共祖先。

这个概念也很好理解

比如[5,1]的最近公共祖先就是3，[6,4]的最近公共祖先是5，[5,4]的最近公共祖先是5。

从思路上说，我们其实就是需要找到一个树，让它的左子树中有p，右子树中有q（或者相反），那么root就是最近公共祖先。

比如6和4，对于根为5的树来说，左子树中有6，右子树中有4，所以它是最近公共祖先。

遍历顺序也可以确定了，是后序遍历，这样才能先确定子树有没有p和q

逻辑也可以写出来：

遇到p或者q就返回它们本身给上一层递归，否则到了叶子节点就返回NULL，同时比较左右子树的返回值

如果返回值都存在，就说明左右子树恰好有pq，那么root就是答案

如果有一边是NULL，那么继续传递另一边的值上去。

拿6和4举例子，在节点2得到左子树为NULL，右子树为4；在节点5得到左子树为6，右子树为4，那么答案就是root5。

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==p||root==q||root==NULL)
            return root;
        TreeNode* left=lowestCommonAncestor(root->left,p,q);
        TreeNode* right=lowestCommonAncestor(root->right,p,q);

        
        
        if(left==NULL&&right!=NULL)
            return right;
        if(left!=NULL&&right==NULL)
            return left;
        
        if(left!=NULL&&right!=NULL)
            return root;
        
        return NULL;
    }