漫谈栈队列及后缀表达式,后缀中缀表达式间的转换
import java.util.Stack;
//计算6 5 2 3 + 8 * + 3 + * ( (2 + 3) * 8 + 5 + 3 ) * 6
/**
* 计算后缀表达式,假定操作数都是常量
* */
public class PostfixEvaluator {
/** 栈 */
private Stack stack;
/** 创建一个新栈 */
public PostfixEvaluator() {
stack = new Stack();
}
/**
* 从左到右扫描表达式,以此标识出每个符号(操作数或操作符)。如果是操作数, 则把它压入栈中。如果是操作符,则从栈中弹出两个元素,
* 并把该操作符应用在这两个元素上,然后把操作结果压入栈中。 当到达表达式的末尾时,栈中所剩域的元素就是该表达式的计算结果。
*
* @param expr 后缀表达式
* @return int 后缀表达式的值
* */
public int evaluate(String expr){
int op1 , op2 , result = 0;
String operator;
//将字符串分解. \\s匹配任何空白字符,包括空格、制表符、换页符等。
String[] takeoperator = expr.split("\\s");//将去掉空格的表达式存入数组中
for(int i = 0 ; i < takeoperator.length ; i++){
operator = takeoperator[i];
if(isOperator(operator)){//判断是该操作符后,使需要被操作的两个数出栈
op2 = stack.pop();
op1 = (stack.pop()).intValue(); //将Integer类型转化为int类型
result = evalSingleOp (operator.charAt(0) , op1 , op2);//计算结果
stack.push(new Integer(result));//把计算结果压入栈中
}else {
stack.push(new Integer(Integer.parseInt(operator)));//压入操作数
}
}
return result;
}
/**
* 计算
*
* @param1 op1 第一个操作数
* @prama2 op2第二个操作数
* @return 计算的结果
* */
private int evalSingleOp(char operator, int op1, int op2) {
int result = 0;
switch (operator) {
case '+':
result = op1 + op2;
break;
case '-':
result = op1 - op2;
break;
case '*':
result = op1 * op2;
break;
case '/':
result = op1 / op2;
break;
}
return result;
}
/**
* 判断是否为操作符
*
* @param token
* @return boolean
* */
private boolean isOperator(String operator) {
return operator.equals("+") || operator.equals("-")
|| operator.equals("*") || operator.equals("/");
}
} 测试类import java.util.Scanner;
public class PostfixEvaluatorTest {
public static void main(String[] args) {
String expression, again;
int result;
try {
@SuppressWarnings("resource")
Scanner in = new Scanner(System.in);
do {
PostfixEvaluator evaluator = new PostfixEvaluator();
System.out.println("请输入一个后缀表达式");
expression = in.nextLine();
result = evaluator.evaluate(expression);
System.out.println();
System.out.println("计算结果为:" + result);
System.out.println("计算另外一个表达式[Y/N]?:");
again = in.nextLine();
if (again.equalsIgnoreCase("n")) {
System.out.println("计算退出!");
}
System.out.println();
} while (again.equalsIgnoreCase("y"));
} catch (Exception e) {
e.printStackTrace();
System.out.println("输入异常,请正确输入后缀表达式,并以空格区分");
}
}
}
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
//转自http://blog.csdn.net/linminqin/article/details/6838026
public class ExpressionTest {
/**
* 优先级比较
*
* @param operator1
* 比较值
* @param operator2
* 被比较值
* @return 小于等于返回false,大于返回true
*/
public boolean comparePrior(String operator1, String operator2) {
if ("(".equals(operator2)) {
return true;
}
if ("*".equals(operator1) || "/".equals(operator1)) {
if ("+".equals(operator2) || "-".equals(operator2)) {
return true;
}
}
return false;
}
/**
* 转为后缀表达式: 1、如果是"("直接压入stack栈。
* 2、如果是")",依次从stack栈弹出运算符加到数组newExpressionStrs的末尾,知道遇到"(";
* 3、如果是非括号,比较扫描到的运算符,和stack栈顶的运算符。如果扫描到的运算符优先级高于栈顶运算符则,把运算符压入栈。否则的话,
* 就依次把栈中运算符弹出加到数组newExpressionStrs的末尾
* ,直到遇到优先级低于扫描到的运算符或栈空,并且把扫描到的运算符压入栈中。就这样依次扫描
* ,知道结束为止。如果扫描结束,栈中还有元素,则依次弹出加到数组newExpressionStrs的末尾,就得到了后缀表达式。
*
* @param expressionStrs
* @return
*/
public String[] toSuffixExpression(String[] expressionStrs) {
// 新组成的表达式
List newExpressionStrs = new ArrayList();
Stack stack = new Stack();
for (int i = 0; i < expressionStrs.length; i++) {
if ("(".equals(expressionStrs[i])) { // 如果是左括号,则入栈
stack.push(expressionStrs[i]);
} else if ("+".equals(expressionStrs[i])
|| "-".equals(expressionStrs[i])
|| "*".equals(expressionStrs[i])
|| "/".equals(expressionStrs[i])) {
if (!stack.empty()) { // 取出先入栈的运算符
String s = stack.pop();
if (comparePrior(expressionStrs[i], s)) { // 如果栈值优先级小于要入栈的值,则继续压入栈
stack.push(s);
} else { // 否则取出值
newExpressionStrs.add(s);
}
}
stack.push(expressionStrs[i]);
} else if (")".equals(expressionStrs[i])) { // 如果是")",则出栈,一直到遇到"("
while (!stack.empty()) {
String s = stack.pop();
if (!"(".equals(s)) {
newExpressionStrs.add(s);
} else {
break;
}
}
} else {
newExpressionStrs.add(expressionStrs[i]);
}
}
while (!stack.empty()) {
String s = stack.pop();
newExpressionStrs.add(s);
}
return newExpressionStrs.toArray(new String[0]);
}
public static void main(String[] args) {
// 前台传过来的字符格式,所以测试也写成这个格式
String expressionStr = "5;+;(;4;-;5;+;1;);-;4;+;(;6;-;5;+;3;);+;2;";
// 分割成表达式数组
String[] expressionStrs = expressionStr.split(";");
String[] newExpressionStrs = new ExpressionTest()
.toSuffixExpression(expressionStrs);
for (int i = 0; i < newExpressionStrs.length; i++) {
System.out.print(newExpressionStrs[i]);
}
System.out.println();
expressionStr = "5;+;(;4;-;5;*;1;);-;4;/;(;6;*;5;+;3;);/;2;";
expressionStrs = expressionStr.split(";");
newExpressionStrs = new ExpressionTest()
.toSuffixExpression(expressionStrs);
for (int i = 0; i < newExpressionStrs.length; i++) {
System.out.print(newExpressionStrs[i]);
}
}
} 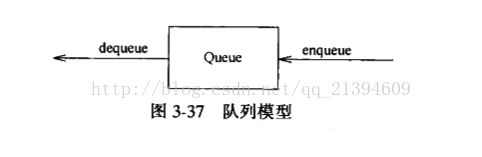
2.队列的应用(部分)
队列通常(但并非一定)以 FIFO(先进先出)的方式排序各个元素。不过优先级队列和 LIFO 队列(或堆栈)例外,前者根据提供的比较器或元素的自然顺序对元素进行排序,后者按 LIFO(后进先出)的方式对元素进行排序。无论使用哪种排序方式,队列的头都是调用 remove() 或 poll()所移除的元素。在 FIFO 队列中,所有的新元素都插入队列的末尾。其他种类的队列可能使用不同的元素放置规则。每个 Queue 实现必须指定其顺序属性。
如果可能,offer方法可插入一个元素,否则返回 false。这与 Collection.add方法不同,该方法只能通过抛出未经检查的异常使添加元素失败。offer方法设计用于正常的失败情况,而不是出现异常的情况,例如在容量固定(有界)的队列中。
remove() 和 poll() 方法可移除和返回队列的头。到底从队列中移除哪个元素是队列排序策略的功能,而该策略在各种实现中是不同的。remove() 和poll() 方法仅在队列为空时其行为有所不同:remove() 方法抛出一个异常,而 poll() 方法则返回 null。
element( ) 和 peek( ) 返回,但不移除,队列的头。
Queue 接口并未定义阻塞队列的方法,而这在并发编程中是很常见的。BlockingQueue接口定义了那些等待元素出现或等待队列中有可用空间的方法,这些方法扩展了此接口。
Queue 实现通常不允许插入 null 元素,尽管某些实现(如LinkedList)并不禁止插入 null。即使在允许 null 的实现中,也不应该将 null 插入到 Queue中,因为 null 也用作 poll 方法的一个特殊返回值,表明队列不包含元素。
Queue 实现通常未定义 equals 和 hashCode 方法的基于元素的版本,而是从 Object 类继承了基于身份的版本,因为对于具有相同元素但有不同排序属性的队列而言,基于元素的相等性并非总是定义良好的。

PS:到这里。。。表这一章算是基本结束了,但最近在学习树的时候毫无头绪,又找了其他的pdf看,发现表,栈,队列的内容不太一样,都是从不同角度进行的讲述。也有在认真的学,之后会把其他地方漏掉的地方补上,希望能够更全面的掌握数据结构。。。看到我的总结的内容的大神们。。觉得总结的如何,有没有能值得回味的地方,希望能私信我文章不足的地方,让我得以改正。。不得不承认代码写的不太多。。。有的地方理解不够深刻,还是希望自己能够反复咀嚼琢磨。
下面放上在网上看到的其他人总结的内容。。不得不说条理要清晰的多。。
---------------------------------------------------------------------------------------------------------------------------
(转)图解数据结构(2)——栈
四、栈(Stack)
前一篇讲解了最基本的东西,这篇就稍微前进一点点,讲一下栈,栈在英文中叫Stack,翻译成中文又叫“堆栈”,但决不能称为“堆”,这个要搞清楚,我们说的“栈”和“堆栈”指的都是Stack这种数据结构,但“堆”却是另外一个概念了,这里且不提。
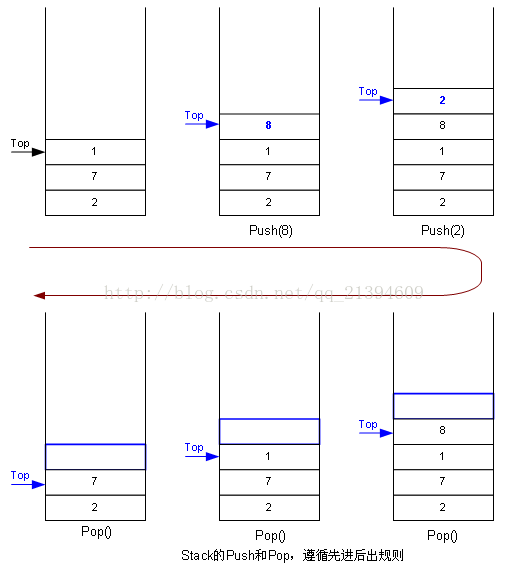
栈最大特点是先进后出,如图:
可以看出,栈有几个最常见的方法,或者说必备的方法,Push,Pop和Top,即进栈,出栈和取最顶元素。从代码上看,栈如何实现呢?用数组好还是用单向链表好呢?其实都可以,我下面的例子是用数组实现的。
说了那么多,栈有什么用呢?下面就举一个最经典的例题——逆波兰表达式(RPN,Reversed Polish Notation)的求解。
什么是逆波兰表达式?我们表述一个算式通常是这样:X+Y,即:“操作数1 操作符 操作数2”,当然也有比较特别的,比如“sqrt(N)”,sqrt是操作符,N是操作数,而逆波兰表达式则很统一,先操作数,后操作符,为什么叫“逆波兰表达式”?因为有一个波兰人发明了波兰表达式,而逆的波兰表达式就叫“逆波兰表达式”了。看下图就能很好理解了
所有的算式都可以用逆波兰表达式写出来,只是我这里的举例是为了方便起见,限制在整数的四则运算里。
那假如现在我们有一个逆波兰表达式,那我们如何求出它的值呢?这里我们的“栈”就要派上用场了,由于操作数在操作符前面,所以我们按顺序遍历这个表达式,遇到操作数的时候进栈,遇到操作符时候让操作数出栈并运算,然后把运算结果进栈。过程如下图所示:
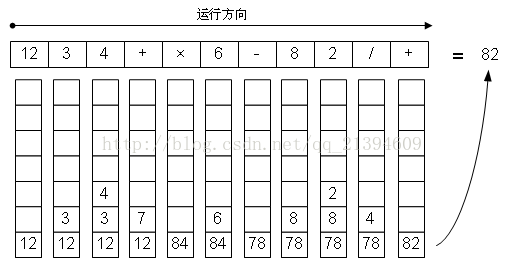
遇到第一个操作符,“+”的时候,由于需要两个操作数,所以出栈两次,4和3出栈,执行加法运算,结果是7,7进栈……依此类推。
#include "stdio.h"
struct Cell
{
int iType; // 0 - number, 1 - '+', 2 - '-', 3 - '*', 4 - '/'
int iData;
};
class Stack
{
public:
Stack(int iAmount = 10);
~Stack();
//return 1 means succeeded, 0 means failed.
int Pop(int& iVal);
int Push(int iVal);
int Top(int& iVal);
private:
int *m_pData;
int m_iCount;
int m_iAmount;
};
Stack::Stack(int iAmount)
{
m_pData = new int[iAmount];
m_iCount = 0;
m_iAmount = iAmount;
}
Stack::~Stack()
{
delete m_pData;
}
int Stack::Pop(int& iVal)
{
if(m_iCount>0)
{
--m_iCount;
iVal = m_pData[m_iCount];
return 1;
}
return 0;
}
int Stack::Push(int iVal)
{
if(m_iCount0 && m_iCount<=m_iAmount)
{
iVal = m_pData[m_iCount-1];
return 1;
}
return 0;
}
int main(int argc, char* argv[])
{
//12 3 4 + * 6 - 8 2 / +
Cell rpn[11] = {
0, 12,
0, 3,
0, 4,
1, 0,
3, 0,
0, 6,
2, 0,
0, 8,
0, 2,
4, 0,
1, 0};
Stack st;
// I won't check the return value for this is just a demo.
int i, iOpt1, iOpt2;
for(i=0; i