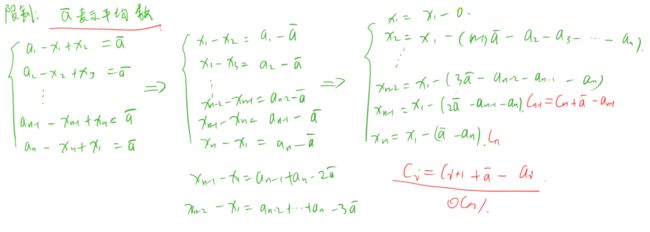蓝桥杯AcWing学习笔记 7-2贪心的学习（下）（附相关蓝桥真题：后缀表达式、灵能传输）(Java)

有参加蓝桥杯的同学可以给博主点个关注，博主也在准备蓝桥杯，可以跟着博主的博客一起刷题。

蓝桥杯

我的AcWing

题目及图片来自蓝桥杯C++ AB组辅导课

贪心（下）

例题

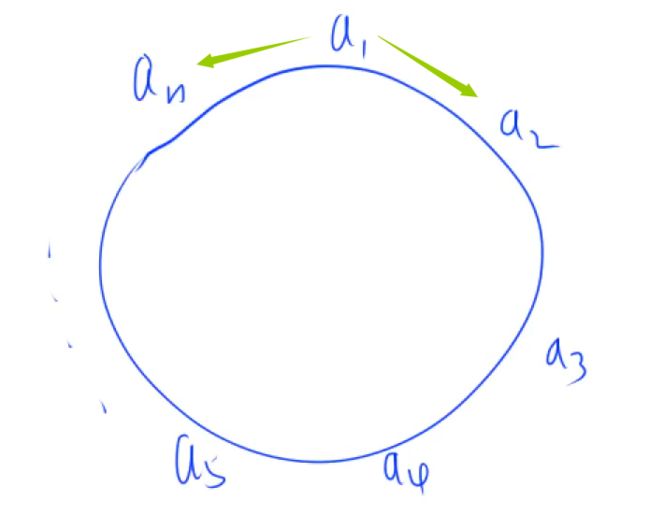
AcWing122.糖果传递

这个题也是很经典的题了，出处很多。

每个小朋友只能给左右两边的小朋友传递糖果，每传递一个糖果代价为1，如果互相传递代价不能抵消。

我们最终希望所有小朋友糖果数量相同，我们如果想达到这个条件的话，通过一个什么样的策略去转移糖果可以使得我们总代价最小。

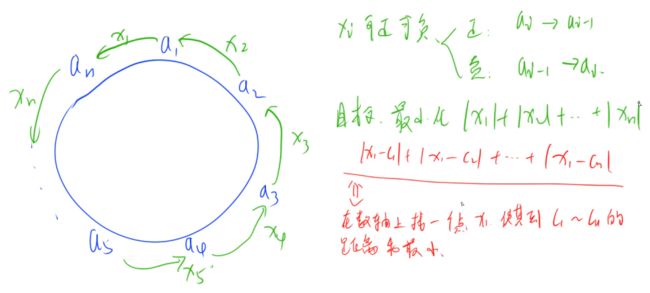
我们看样例，1 2 4 5 总数12，每个小朋友应该有3个糖果：

代价是4。

其实这个题可以转换为这题AcWing 104. 货仓选址，我们还是要落实在数学模型上。

最后问题转换成了一个数轴上取中位数的问题，X1只要取C1 ~ Cn的中位数即可。

import java.util.Scanner;
import java.util.Arrays;

public class Main {
    
    static final int N = 1000010;
    static int[] a = new int[N];
    static int[] c = new int[N];
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        for (int i = 1; i <= n; i++) a[i] = sc.nextInt();
        
        long sum = 0;
        for (int i = 1; i <= n; i++) sum += a[i];
        
        long avg = sum / n; // 求a[]的平均值
        for (int i = n; i > 1; i--) c[i] = c[i + 1] + (int)avg - a[i]; // 公式
        c[1] = 0; // C1要初始化为0（这句话可加可不加 因为数组定义在全局变量）
        
        Arrays.sort(c, 1, n + 1);
        
        long res = 0;
        for (int i = 1; i <= n; i++) res += Math.abs(c[i] - c[(n + 1) / 2]); // 这里需要上取整
        
        System.out.print(res);
    }
}

---

AcWing112.雷达设备

本题是基于区间的贪心。

小岛在海的一侧，雷达在海岸线上，检测范围是d，建立xy轴，给出岛的坐标以及雷达的检测范围，求把所有小岛全部覆盖最小的雷达数目。

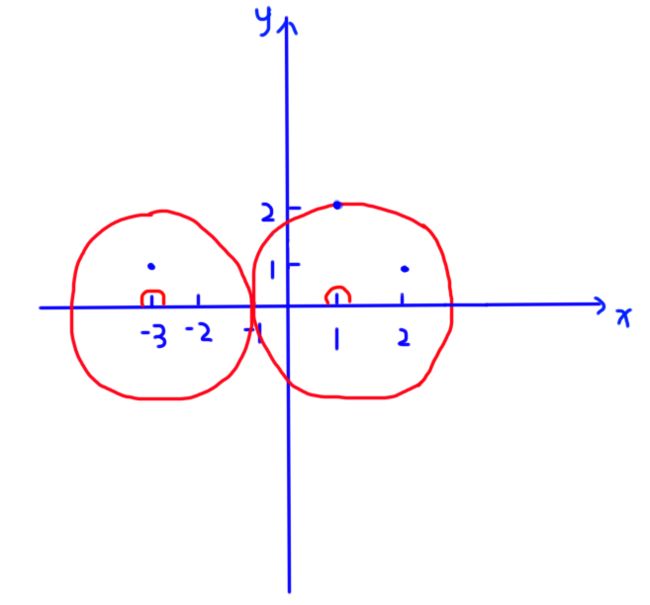
我们画一下第一个样例：

我们用2个雷达可以将小岛全部覆盖。

直接想的话很麻烦，因为还有圆的问题，我们想判断雷达能够覆盖哪些点，需要遍历一遍所有点；

但我们可以做一下逆方向的转化，我们不去考虑这个雷达能覆盖到的小岛，看一下对于每个小岛我雷达要放到什么位置上才可以覆盖到这个小岛，不从雷达的角度去找小岛，而是从小岛的角度去找雷达。

对于(1, 2)这个点来说，雷达只能建在$(1,0)$这个位置，因为这个点的y是2，所以这里必须要有一个雷达；

对于(2, 1)这个点来说，雷达可以建在$(2-\sqrt{3},0),(2+\sqrt{3},0)$之间

对于(-3, 1)这个点来说，雷达可以建在$(-3-\sqrt{3},0),(-3+\sqrt{3},0)$之间

因此我们通过这样的转化，变成了给定若干区间，最少选多少个点，可以使得每个区间上最少选一个点。

贪心策略：

① 将所有区间按右端点排序

② 按照排序的顺序扫描每一个线段

情况1：如果上一个点不在区间中，则选右端点（因为最后面的区间更大，更有可能覆盖更多后面的区间）
情况2：如果上一个点在区间中，则跳过

举例证明：

第一个区间是最开始的，所以我们直接选择它的 右端点，这样它会包含住第二个区间和第三个区间的前一部分，也就是这个点在这两个区间中，可以直接跳过；但到了第四个区间我们没法覆盖到它的前一部分，所以这里再选择第四个区间的右端点，让它尽可能多的包含住后面的区间，到了第五个区间由于是最后的区间，我们就直接选择它的右端点。

对于第一个样例证明：

第一个区间直接选右端点，对于第二个区间上一个点并未在区间中，所以选第二个区间的右端点，对于第三个点因为上一个点在区间中，所以跳过，总点数为2。

import java.util.Scanner;
import java.util.Arrays;

public class Main {
    
    static final int N = 1010;
    static Segment[] seg = new Segment[N];
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int d = sc.nextInt();
        
        boolean failed = false;
        for (int i = 0; i < n; i++) {
            int x = sc.nextInt(), y = sc.nextInt();
            if (y > d) failed = true;
            else {
                double len = Math.sqrt(d * d - y * y); // 求一半区间的长度
                seg[i] = new Segment(x - len, x + len);
            }
        }
        
        if (failed) System.out.print(-1);
        else {
            Arrays.sort(seg, 0, n);
            
            double last = -1e20; // 尽可能小，因为要与第一个区间的左端点比较
            int cnt = 0;
            for (int i = 0; i < n; i++) {
                if (last < seg[i].l) {
                    cnt++;
                    last = seg[i].r; // 取右端点
                }
            }
            
            System.out.print(cnt);
        }
    }
    
    static class Segment implements Comparable<Segment> {
        double l;
        double r;
        
        public Segment(double l, double r) {
            this.l = l;
            this.r = r;
        }
        
        public int compareTo(Segment o) {
            return Double.compare(r, o.r);
        }
    }
}

第十届2019年蓝桥杯真题

AcWing1247.后缀表达式

JavaB组第9题

后缀表达式也被称为逆波兰表达式。

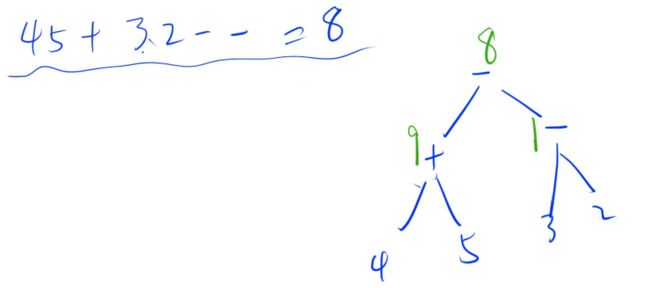
这个题用栈模拟一下会更好理解，我们来举一个样例：$45+32--$

如果是数的话直接入栈，如果是符号的话就将栈顶两个元素弹出进行表达式求值。

最终结果是8。

栈的知识可以参考我之前写的这篇文章：数据结构学习笔记 1-3栈概述与递归及LeetCode真题图解（Java）

里面也讲了一下表达式求值转换成树的形式，二叉树的后序遍历就是我们的表达式。

这个题有N个加号、M个减号，以及正负都可能有的整数，我们最直观的想，要把所有的负数都减去，把所有的正数都加上，才有可能达到最大值，但是真的是这样的吗？

① $M=0$，没有减号，所有数全部相加

② $M>0$，有减号时，表面上是M个减号，其实我们可以凑出1 ~ M个减号。

我们可以凑出来加号，在上面构建一个b：

这样就由4个减号变为1个减号了，我们可以把里面的某一个负数拿出来，变为2个减号，我们可以在1 ~ M之间任意构建。

③ $M>0$，$N>0$，有减号也有加号时，我们可以凑出1 ~ M + N个减号（我们可以把正数拼在上面的括号里，变为减号）

分析到这一步剩下的问题就很简单了，看一下一共有多少个负数，尽可能给每个负数配一个减号，给每个正数配一个加号。

因为我们至少有一个减号，第一个数一定是加的，所以至少减一个数、加一个数，所以要减的话一定要减去我们的最小值，加我们的最大值。

import java.util.Scanner;
import java.util.Arrays;

public class Main {
    
    static final int N = 200010; // 总数的个数是n + m，所以要开20w
    static int[] a = new int[N];
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int k = n + m + 1;
        for (int i = 0; i < k; i++) a[i] = sc.nextInt();
        
        long res = 0;
        if (m == 0) for (int i = 0; i < k; i++) res += a[i];
        else {
            
            Arrays.sort(a, 0, k); // 也可以不排序 找出最大值和最小值即可
        
            res = a[k - 1] - a[0]; // 先加最大值减去最小值
            for (int i = 1; i < k - 1; i++) res += Math.abs(a[i]); // 仅剩的一个减号已经用过了 所以直接加绝对值即可
        }
        System.out.print(res);
    }
}

---

AcWing1248.灵能传输

JavaB组第10题

本题难度有点大，我没有做，可参考AcWing题解。

import java.io.*;
import java.util.*;

public class Main{
    
    static int N = 300010;
    static long[] s = new long[N];
    static long[] a = new long[N]; // 保存最终的序列
    static boolean[] st = new boolean[N]; // 用于判断某个点是否被访问过了
    static int T;

    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        T = Integer.parseInt(in.readLine());

        while (T-- > 0) {
            int n = Integer.parseInt(in.readLine());

            String[] arr = in.readLine().split(" ");
            s[0] = 0;
            for(int i = 1; i <= n; i++) s[i] = s[i - 1] + Long.parseLong(arr[i - 1]);
            // 初始化s0和sn
            long s0 = s[0]; long sn = s[n];
            if (s0 > sn) { // 如果s0的值大于sn，就交换两者的值
                long temp = s0;
                s0 = sn;
                sn = temp;
            }
            Arrays.sort(s, 0, n + 1);

            // 寻找s0的位置
            for (int i = 0; i <= n; i++) {
                if (s[i] == s0) {
                    s0 = i;
                    break;
                }
            }

            // 寻找sn的位置
            for (int i = 0; i <= n; i++) {
                if (s[i] == sn) {
                    sn = i;
                    break;
                }
            }

            Arrays.fill(st, false); // 初始化st数组

            int l = 0, r = n;
            for (int i = (int) s0; i >= 0; i -= 2) {
                a[l ++] = s[i];
                st[i] = true;
            }
            for (int i = (int) sn; i <= n; i += 2) {
                a[r--] = s[i];
                st[i] = true;
            }
            for (int i = 0; i <= n; i++) {
                if (!st[i]) {
                    a[l ++] = s[i];
                }
            }

            long res = 0;
            for(int i = 1; i <= n; i++) res = Math.max(res, Math.abs(a[i] - a[i - 1]));

            System.out.println(res);
        }
    }
}

有对代码不理解的地方可以在下方评论