leetCode 115.不同的子序列 动态规划 + 滚动数组(优化)
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 10^9 + 7 取模
示例 1:
输入:s = "rabbbit", t = "rabbit" 输出:3 解释:如下所示, 有 3 种可以从 s 中得到 rabbit" 的方案
rabbbitrabbbitrabbbit
示例 2:
输入:s = "babgbag", t = "bag" 输出:5 解释:如下所示, 有 5 种可以从 s 中得到 "bag" 的方案babgbagbabgbagbabgbagbabgbagbabgbag
>>思路和分析
下文参考(~ ̄(OO) ̄)ブ笨猪爆破组的文章解法和文字:115. 不同的子序列 - 力扣(LeetCode)
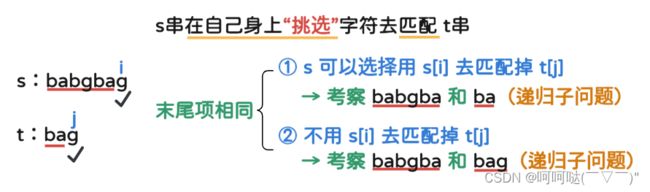
在s串身上“挑选”字符,去匹配 t串 的字符,求挑选的方式数
(1)递归思路:抓住“选”,s 要按照 t 来挑选,逐字符考察“选”或“不选”,分别来到什么状态?
- 1.s[i] == t[j]
- 举例:s 为 babgbag,t 为 bag,末尾字符相同,故 s 有两种选择
- 注意:int n = s.length(),m = t.length();
- 1.用s[n-1] 去匹配掉 t[m-1],问题规模缩小:继续考察 babgba 和 ba
- 2.若s[n-1] 不去匹配掉 t[m-1],可由于t[m-1] 仍需被匹配,于是在 babgba 中继续挑,考察babgba 和 bag
- 是否用s[n-1]去匹配t[m-1],是两种不同的挑选方式,各自做下去所产生的方式数,相加起来,是大问题的解
- 2.s[i] != t[j]
- s[i] 不匹配 t[j],唯有拿 s[i] 之前的子串去匹配
(2)递归函数返回
返回: 从开头到s[i]的子串中,出现『从开头到t[j]的子串』的次数。 即,从 前者 选字符,去匹配 后者 的方案数
(3)递归树底部的base case
一步步地递归压栈,子问题规模(子串长度)在变小:
- 小到 t 变成空串,此时 s 去匹配它,方式只有一种:就是什么字符都不用挑(或 s 也是空串,啥也不用做也可匹配,方式数也是1)
- 小到 s 变成空串,但t不是, s 是没有办法匹配 t 的,方式数为0
递归函数的参数可以传子串或索引:这里推荐用索引描述子问题,因为不用每次都切割字符串,也更容易迁移到dp解法去
一、递归搜索 (会超时)
- 超出时间限制
class Solution {
public:
// 递归搜索 (会超时)
int numDistinct(string s,string t) {
const int n = s.length(),m = t.length();
function dfs = [&](int i,int j) -> int {
if(j<0) return 1;// base case
if(i<0) return 0;// 这两个base case 的顺序不能调换!因为 i<0 且 j<0 时 应该返回1
if(s[i] == t[j]) return dfs(i-1,j) + dfs(i-1,j-1);
else return dfs(i-1,j);
};
return dfs(n-1,m-1);
}
}; 二、递归搜索 + 保存计算结果 = 记忆化搜索
- 二维memo数组 存储计算过的子问题的结果
// 递归搜索 + 保存计算结果 = 记忆化搜索
int numDistinct(string s, string t) {
int n = s.length(),m = t.length(),memo[n][m]; // 二维memo数组 存储计算过的子问题的结果
memset(memo,-1,sizeof(memo));// -1 表示没有访问过
function dfs = [&](int i,int j) -> int { // 从开头到s[i]的子串中,出现『从开头到t[j]的子串』的 次数
if(j<0) // base case 当j指针越界,此时t为空串,s不管是不是空串,匹配方式数都是1
return 1;
if(i<0) // base case i指针越界,此时s为空串,t不是,s怎么也匹配不了t,方式数0
return 0;
if (memo[i][j] != -1) // memo中有当前遇到的子问题的解,直接拿来返回
return memo[i][j];
if (s[i] == t[j]) { // t[j]被匹配掉,对应dfs(i-1, j-1),不被匹配掉对应dfs(i-1, j)
memo[i][j] = dfs(i-1, j) + dfs(i-1, j-1);
} else {
memo[i][j] = dfs(i-1, j);
}
return memo[i][j];// 返回当前递归子问题的解
};
return dfs(n-1,m-1);//从开头到s[n-1]的子串中,出现『从开头到t[m-1]的子串』的次数
} 也可以写成这样的代码:
class Solution {
public:
// 递归搜索 + 保存计算结果 = 记忆化搜索
int numDistinct(string s, string t) {
int n = s.length(),m = t.length(),memo[n][m];
memset(memo,-1,sizeof(memo));
function dfs = [&](int i,int j) -> int {
if(j<0) return 1;
if(i<0) return 0;
int &res = memo[i][j];
if (res != -1) return res;
if (s[i] == t[j]) return res = dfs(i-1, j) + dfs(i-1, j-1);
return res = dfs(i-1, j);
};
return dfs(n-1,m-1);
}
}; 三、动态规划 与 递归 的区别
- 递归公式
if (s[i] == t[j]) {
memo[i][j] = dfs(i-1, j) + dfs(i-1, j-1);
} else {
memo[i][j] = dfs(i-1, j);
}递归是自上而下调用,子问题自下而上被解决,最后解决了整个问题,而dp是从base case 出发,通过在dp数组记录中间结果,自下而上地顺序地解决子问题
- dp解法
1.确定dp数组(dp table)以及下标的含义
dp[i][j]:从开头到s[i-1]的子串中,出现『从开头到t[j-1]的子串』的 次数。即:
- 前 i 个字符的 s 子串中,出现前 j 个字符的 t 子串的次数
- 或者说 以i-1为结尾的s子序列中出现以j-1为结尾的 t 的个数
2.确定递推公式
状态转移方程:
- 当s[i-1] != t[j-1]时,有dp[i][j] = dp[i-1][j]
- 当s[i-1] == t[j-1]时,有dp[i][j] = dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
3.dp数组初始化
base case
j==0时,dp[i][0] = 1i==0时,dp[0][j] = 0
也可从递推公式dp[i][j] = dp[i-1][j-1] + dp[i-1][j];和dp[i][j] = dp[i-1][j];中可以看出dp[i][j]是从上方和左方推导而来的,故:dp[i][0] 和 dp[0][j] 是一定要初始化的
4.确定遍历顺序
从递推公式我们可以看出dp[i][j]是从上方和左方推导而来的,所以遍历的时候一定是从上到下、从左到右,可以保证dp[i][j]可以根据之前计算出来的数值进行计算
5.举例推导dp数组
以s:"heeeheheda",t:"heheda"为例,推导dp数组状态如下(可以参考此图,在不知道递推式的情况下找出规律,手推递推式):
以s:"babgbag",t:"bag"为例,推导dp数组状态如下:
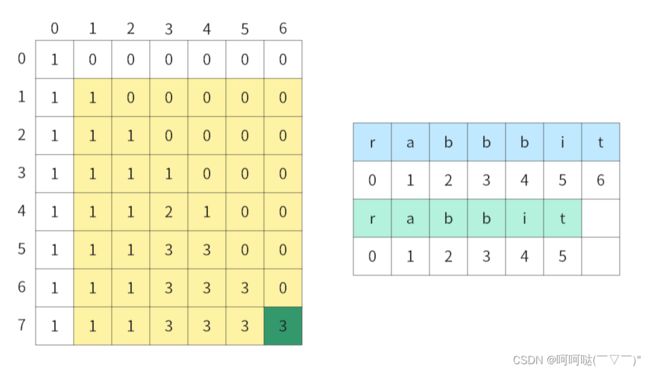
以s:"rabbbit",t:"rabbit"为例,推导dp数组状态如下:
(一)动态规划 二维dp
class Solution {
public:
// 动态规划 二维dp数组
int numDistinct(string s, string t) {
int n = s.length(),m = t.length();
uint64_t dp[n+1][m+1];
memset(dp,0,sizeof(dp));
for(int i=0;i- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
(二)动态规划 二维dp 优化空间复杂度
class Solution {
public:
// 动态规划 二维dp优化空间复杂度
int numDistinct(string s, string t) {
int n = s.length(),m = t.length();
uint64_t dp[2][m+1];
memset(dp,0,sizeof(dp));
for(int i=0;i<2;i++) dp[i][0] = 1;
for(int j=1;j- 时间复杂度: O(n * m)
- 空间复杂度: O(m)
(三)动态规划 一维dp(滚动数组) 优化空间复杂度
class Solution {
public:
// 动态规划 一维dp 优化空间复杂度
int numDistinct(string s, string t) {
int n = s.length(),m = t.length();
uint64_t dp[m+1];
memset(dp,0,sizeof(dp));
dp[0] = 1;
for(int j=1;j=1;j--) {
if(s[i-1] == t[j-1]) dp[j] = dp[j-1] + dp[j];
}
}
return dp[m];
}
}; - 时间复杂度: O(n * m)
- 空间复杂度: O(m)
参考和推荐文章、视频:
115. 不同的子序列 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
动态规划之子序列,为了编辑距离做铺垫 | LeetCode:115.不同的子序列_哔哩哔哩_bilibili