06. 机器学习入门2 - 理解特征和向量

Hi, 你好。我是茶桁。

上一节课，咱们用一个案例引入了机器学习的话题，并跟大家讲了一下「动态规划」。

那这节课，我们要真正进入机器学习。

机器学习初探

在正式开始之前，我们来想这样一个问题：我为什么要先讲解「动态规划」，然后再引入机器学习呢？

原因其实是这样：曾经有一度时间，差不多一九七几年开始，大概有三十四年，动态规划其实可以变成图和树的问题。计算机科学里，图和树其实是占主流的，人们去解决图像的分割，图像的分类，文本的识别，文本的分类问题，有很大一部分都会将其优化为图和树的问题去解决。包括上两节课中我们提到的李开复去解决语音识别的问题，也是拆分成语言树。

为什么要优化成图和树来解决呢？因为这个技术在当时非常的成熟。但是，因为有了图和树，那么依照我们上一节的分析，树会继续向下细分成更小的树，也就是会形成子图。

所以，人们就会发现，当我们将问题优化成图和树之后，再使用动态规划，就能让问题加速解决。也就是像我们上节课中所讲的一样。有时候，甚至不用动态规划都无法解决。

可是动态规划是有局限的，当问题过度复杂的时候，使用动态规划也开始解决不了了。

这个问题的一个非常经典的案例是一九九几年的时候，当时电子邮件开始兴起，也就催生了一个非常重要的产业，就是垃圾邮件。因为垃圾邮件成本很低，只要有一个服务器，然后不断的发送就可以了。

比如邮件内容可以写：

因为你经常上网，我获得了你的一些账户密码，我已经将你的一些见不得人的浏览记录都记录下来了，需要你在三天之内，向某个账户转多少多少钱，否则我将公布你的所有记录。

我知道，你们肯定会有人觉得：这么弱智的诈骗邮件都能得逞啊？但其实是能得逞的，垃圾邮件不像诈骗电话，还需要人拨。当然，我知道现在诈骗电话都不需要人值守了，只要有一个电脑连上电话服务，然后AI会自动打电话，通过AI合成语音就可以。但是当时那个年代可没有这个，发邮件相对就简单很多，只需要有一个服务器在那不断的发送就行了。

家在之前的数学课中应该都学过概率了。这里也就涉及到了一个概率问题，我发10000个邮件，哪怕只有一个人会上钩，那我也会挣钱。所以当时发送垃圾邮件是一个很大的产业。

既然有人为这个东西所困扰，就会有人想着用通过正当的方式去挣钱。当时网易的163，还有美国最早的各种邮箱比如Hotmail等等，都提供了一个功能是付费提供拦截垃圾邮件的功能。

当时垃圾邮件可以多到整个互联网上收到的99.8%的邮件都是垃圾邮件。如果不花钱，基本上都用不了邮箱，因为邮箱地址也是可以随机生成的。

结果像什么163，还有Hotmail等等，要去攻克垃圾邮件，而垃圾邮件要去绕开他们的防锁，要能诈骗到钱。就进行了这样的反复的斗争。

那这个时候的程序员是怎么做的呢？很简单，他们用的想法也是一样，就是要分析文字，分析语法，把它变成文字树，语法树，变成文本关系。

我们想想，垃圾邮件规律是不是基本上找不到？只要找到一种规律它马上可以变。就算找到了一种规律，把它写成代码了，但是做垃圾邮件的人很快就可以攻克。

当时人们就很头疼，完全没有办法。用这种分析的方法，用类似于动态规划等的分析方法解决不了。

当时哈佛大学有一个老师用了一种方法，叫做基于统计的文本：贝叶斯分析方法，来判断一个邮件是不是垃圾邮件。

他说，不要人工去定规则，不要人工去分析，去找规则。假如在这里找到2万个垃圾邮件，然后现在来了一条新的邮件，我不知道内容，但是可以根据以前这2万个垃圾邮件，根据它里边的这个文本的内容，文字，看一下之前的垃圾邮件里出现的次数到底是多少，就可以进行贝叶斯分类。

也就是说，里面的单词分别在垃圾邮件里出现了多少次，出现次数多不多等等。这个时候就可以给他一个概率，比方说是垃圾邮件的概率是0.7，非垃圾邮件的概率是0.3，那就可以判定是垃圾邮件。

在以前，人们都是写一个方法来判断是或不是，而现在则是变成了一种概率。

结果人们就发现这样非常好做，这样做其实也做不到100%正确。虽然做不到100%正确，但是可以做一个比较高的准确度，可以拦截大部分垃圾邮件。

而且它可以自动更新，只要把这个程序放这，不断的有垃圾邮件进来，样本库越来越多，接下来再收到新的邮件，就能够知道这个是不是垃圾邮件了。

当时大家还会融入统计分析方法，后来人们就发现根据原来的这些信息提炼出一些数据，让机器自动或半自动的提炼出一些信息，然后去预测新问题。这个过程就特别像小孩学习的时候，你给他很多知识他自己去学，学完之后去解决没有见过的问题。

这种解决问题的方法，后来就叫做机器学习。我们就把解决这种问题的整个方法就叫做机器学习。

之前的这一些内容，也就是咱们机器学习产生的背景。

特征和向量

对于整个世界上的所有东西来说，都是可以被量化的。在管理学上有一个东西叫做 if one thing cannot be measure， it cannot be managed。就是一个事情如果不能被量化，它就不能被管理。

在科学上其实也有一个，笛卡尔当年就说过，如果一个东西不能被量化，那么它就不能被分析。

比方说一个人，要衡量这个人，要刻画这个人的特点，你可以给出特点。例如说身高一米73，月收入18000。假如我们用0和1来表示，到底是男还是女, 200910表示的可能是住址编码，28可能是年龄。

这个时候我们就会得到一个东西，如果我们把一位男士的信息抽象成这样一个向量。

假如有另外一个向量，这个向量我们把叫做man2。如果man2和man的向量的距离是接近的，我们就知道其实它里边的数值是接近的。因为它的向量的计算值比较小，意味着每一个对应的两个数字之间比较小。

所以当我们把一个一个的对象能够量化，变成一个向量之后，我们就能够知道哪些向量之间是相似的，哪些对象之间是相似的。

除此之外，不仅是人，还可以把邮件也处理一下。

假如说一封邮件里面包含了213个字符，包含了1个关键字，标题长度为27，0个抄送地址。那么邮件也是可以向量化，各种东西都可以被向量化。

向量化之后就可以有一个什么样的结果呢？假如存在一种函数：
f 1 ( m a n → = [ 1.75 18000 1 200910 28 ] ) \begin{align*} f_1 \begin{pmatrix} \overrightarrow {man} = [ \\ \\ 1.75 \\ \\ 18000 \\ \\ 1 \\ \\ 200910 \\ \\ 28 \\ \\ ] \end{pmatrix} \end{align*} f1​ ​man =[1.7518000120091028]​ ​​

我们来看上面这个式子，这一串数字代表的是我们现实生活中的一个对象。这个函数现在我们虽然不知道它是啥，但是我们知道输入一个向量给到一个函数，这个函数可以产生出不同的东西。

假如这个函数返回0.75， 或者是1.38，负一点几等等。只要是个连续的数字，属于R。这个函数就是一个回归函数，Regression。

一个函数，它返回出来的只有+1和-1， 或者只有0和1两种结果。我们就把它叫做二分类。

如果返回3个值，这三个值加起来等于1，每一个表示的是某个东西的概率，那我们把这个叫做多分类。

分类函数和回归函数是机器学习里边最典型的两个函数。

分类函数大家好理解，它给出来的结果表示的是类别的概率。例如说是1就表示可能是a类别，-1可能是b类别。

0.2、0.7、0.1表示三类，第二类的概率最大。

Regression，回归是什么意思呢？

回归这个词当年其实是一个生物学概念，一个遗传学概念。指的是生物的下一代的特征会更偏向于群体的平均值。

比方说姚明两米多，一个正常人的身高是1米75,那么姚明的儿子的身高大概率会向着1米75这个方向变,而不会变得更高。也就是说姚明的儿子大概率会比姚明低。一个人个子特别矮，他儿子大概率呢会比爸爸高。这个就叫做回归现象。

与此同时，其实在我们的整个职业发展中也有这样的情况。假如说一个人特别优秀，大概率他儿子不会像他那么优秀，生物学上把这个遗传线叫做回归。

后来呢生物学家、包括心理学家就发现回归其实本质上是我们的平均值，整体趋势的平均值。所以当时统计学家也用了这个词，他们把群体趋势就叫做Regression，就叫做回归。

后来在机器学习里，所谓的群体趋势其实就是，假设我们现在有这么多点：

现在这个群体的趋势假设是这样，我们拟合了一个函数f(x)（红色直线）。 那么我们输入一个f(x)输入到这条直线里面, 就可以得到一个实数的输出，这样的过程就叫做Regression。

当我们输入一个数字的时候，不仅可能会输出概率，可能还会输出一连串东西。

例如我们现在是一个决策问题，输入了一个情况到一个函数里面，要预测接下来我们该怎么办。

我们输入了行动1、行动2、行动3、行动4…，我们把这种学习问题叫做sequence，就是序列问题。

比如输入的是1、2、3、4这四个人的信息，输出是3、2、4、1，给这四个人排了个序。这种排了个序的事情我们就把它叫做rank，尤其是在推荐系统，在搜索引擎里面用的非常非常多。同理，输入一个Email其实也可以做这样的事情。

那我们一起来想一下，假设我们有一个f(x)，f(x)具体怎么实现先不管。假设存在一个f(x), 如果我们要让f(x)执行一个Regression的任务，可以想一下，这个f(x)可以是在什么场景下。
f ( x ) ( e m a i l → = [ 213 1 27 0 ] ) \begin{align*} f(x) \begin{pmatrix} \overrightarrow {email} = [ \\ \\ 213 \\ \\ 1 \\ \\ 27 \\ \\ 0 \\ \\ ] \end{pmatrix} \end{align*} f(x) ​email =[2131270]​ ​​

举个例子，比方说要让f(x)执行一个rank任务，它的场景是这里有十封未读邮件，要排个序。要输出哪些邮件最紧急，然后去回复。这就是一个rank的场景。

再举一个例子，如果这个f(x)要执行的任务是一个多分类任务，可以是在什么场景下。就是邮件分组对吧？所以我们可以看到，只要我们可以把一个一个对象表示成向量，当我们有一个函数的时候，就可以执行各种各样的任务了。

那我现在问，如果这个f(x)要做Regression，可能是哪个场景呢？

机器学习其实就是反反复复的在做这么一件事情，就是让机器半自动的得到这个f。注意是半自动，它并不能全自动。

在求解f的过程中，我们需要输入一个x，真正的值是多少是有标准答案的。f算的对还是错，是有标准答案的。

比方说贝叶斯、SBM、决策树、神经网络，这些其实都是一种f。里边这些关键参数是机器自动获得的，但是到底这个函数类型是什么，是概率式、还是if else的，还是神经网络，这种形式得人来定。

f有标准答案，是有对错的。我们把这种有对错的求解函数的方法叫做监督学习。

为什么有对错就要监督学习呢？就是在整个学习过程中，也就是整个获得f的过程中，我们会不断的监督他，看他学对了还是学错了。如果学对了就给他沿着正确的方向继续走，如果学错了就要换一个方向。这就叫监督学习。

除了监督学习之外，还有一种机器学习的方法，是让机器自动去归类。
$$\begin{array}{r}man01man02man03man04\\ man05man06man07man08\\ man09man10man11man12\\ man13man14man15man16\end{array}$$

假如有很多人，我们希望机器能自动的把这些人根据某些特征自动的进行一个分类。在这个过程中，其实是没有标准答案的，是机器根据这些向量自动分类的。我们把这种学习方式叫做非监督学习，也叫做聚类。

非监督学习的难点就是我们不太好衡量，到底是不是对的，还是错的。万一这个分类不是我们需要的分法，就只能改变参数让它再分一遍了。

所以，非监督学习不好量化，它的结果只能作为参考，没有标准答案。

机器学习的通用框架

不管是做什么机器学习，不管是在小公司还是大公司，还是在航空航天局。不管是在哪里，我们都有一个通用的方法。

首先，observed data, 会有一些观察到的数据。观察到的数据之后我们就要进行一件叫做特征提取的事情。特征提取就是把我们观察到的这些数据变成一个一个向量。

观察到的是路边上的一个一个的人，我们要把这一个一个的人变成一条一条的向量。变成向量之后就要进行所谓的学习。这个学习就是需要根据原来的向量，在人的指导下去优化一些函数，得到一些函数的参数。

然后这个函数要能预测新的没有见过的，也就是New Data部分，是没有见过的一些新数据，要能得到结果，图中就是得到y。这是我们整个学习的过程，整个机器学习基本上都是这样的一套流程。

那什么叫做监督学习呢？监督学习就是在学习的这个过程中，每次为了获得f，会输入一对一对的x和y。y就指的是我们在训练的时候，我们已知的这些数据的x以及对应的值。

通过这些大量对应的值，机器自动去总结规律，抽象规律得到f。

监督学习就是在学习的时候我们会给到机器x和y, y就指的是这个x对应的值。而非监督学习就不提供这些东西。

非监督学习只提供x，经过x之间的向量的距离近不近等等，自动的去获得x的分类。

梯度下降

在这个求解f的过程中，监督学习的时候有一个非常非常重要的方法叫做「梯度下降」。

梯度下降是一个非常重要的点，之后的课程中咱们会讲到。

假如我们有一组k和b，输入一个x可以得到一个y。假如就是kx+b = y，我们现在其实是想求一组k和一组b，能够使得我们输入任意的x的时候得到的值都任意的和y接近。

还是拿上边这个函数来讲，比如f(x) = kx + b, 我们现在想求一组k和一组b,让它和y的值越接近越好。我们怎么来评价它越接近越好呢？ 写一个函数 $\sum [(kx+b)-y{]}^2$，这个我们把它叫做loss函数：$loss=\sum [(kx+b)-y{]}^2$ ，表示这个值如果越大我们信息差的越多，这个值越小就表示我们信息保留的越好，丢失的越少。

其实原理就是要获得一组k和b，然后使得loss取最小值。为了求得一组k和b，让这组k和b能够使我们的函数最接近于我们真实的值，可以给他一个随机值，然后让loss去给k求偏导。

如果此时此刻求出来的偏导是大于0的，就是随着k的减小，loss值要减小。如果loss对k的偏导小于0，意味着随着k的增大，loss要减小。

那新获得的k就等于原来的k加上loss给k求偏导的相反数。
$$k_2=k_1+(-1)\frac{\partial loss}{\partial k}\times \propto$$

当然我们最后乘上了一个系数，这个系数必须是一个很小的数字，比如说是0.001。这个系数的作用是什么遇到的一些函数，偏导特别大，但是此时我们其实已经很接近那个最优点了，可是偏导特别的垂直。那在这里就要加一个很小的系数控制一下。

这里要说一下，这个部分不能死记公式，没什么所谓的公式，都是一些比较基础的数学知识。这也就是为什么我之前花那么久来写数学基础的原因。

另外就是，在数学基础之上，要拿出你的笔和纸，当然平板也可以，要多画画，然后你就懂了。如果这个东西不多动笔，觉得要背下来，劝你趁早别干这行了，也别学了，可以去做个文职的工作，就天天背书就可以了。现在学的这些东西一定是要内化的，一定要拿着笔多练，多敲代码。

与此类似的，b也可以做这样的运算，$b_2=b_1+(-1)\frac{\partial loss}{\partial b}\times \propto$。这样，经过我们不断地输入x和y，就能够慢慢地找到一组最优的k和b了。这个，就是梯度下降所做的事情。

接下来，咱们就演示一下梯度下降的意义。

我们现在有一个loss函数，这个函数会返回一个运算结果如下：

def loss(k):
    return 3 * (k ** 2) + 7 * k - 10

现在对于k的偏导，我们把2放下来，那就是6*k，再加上7:

def partial(k):
    return 6 * k + 7

这个就是它的偏导。

现在给他随机出一个值, 为了让数据更明显，我们将范围定在(-10, 10)之间。顺便给一个很小的系数alpha

import random
k = random.randint(-10, 10)
alpha = 1e - 3 # 0.001

接着，我们来做循环。之前咱们分析过整个式子，直接将其写出来就可以了，最后是打印出k和loss(k)：

k = k + (-1) * partial(k) * alpha
print(k, loss(k))

将这一段代码扔到循环里，为了更明显，我们让它循环100次，完整代码如下：

import random

def loss(k):
    return 3 * (k ** 2) + 7 * k - 10

def partial(k):
    return 6 * k + 7

k = random.randint(-10,10)
alpha = 1e-3 # 0.001

for i in range(100):
    k = k + (-1) * partial(k) * alpha
    print(k, loss(k))

---
-9.947 217.19942699999993
-9.894317999999998 214.43236005537193
-9.841952091999998 211.69839829966944
-9.789900379447998 208.99714566241215
...
-6.064345358065952 57.87843635922653
-6.034959285917557 57.01748574662477
-6.005749530202052 56.16683554715212

我们可以看到它的值一直在下降，虽然不能直接求解出最好的那个k是什么，但是通过梯度下降这样的方法，一步一步的慢慢的就找到了这个函数的最小值。

当我们把循环次数再次提升到100000的时候，我们来看看最后的结果：

for i in range(100000):
    k = k + (-1) * partial(k) * alpha
    print(k, loss(k))

---
...
-1.1666666666666852 -14.083333333333332
-1.1666666666666852 -14.083333333333332
-1.1666666666666852 -14.083333333333332

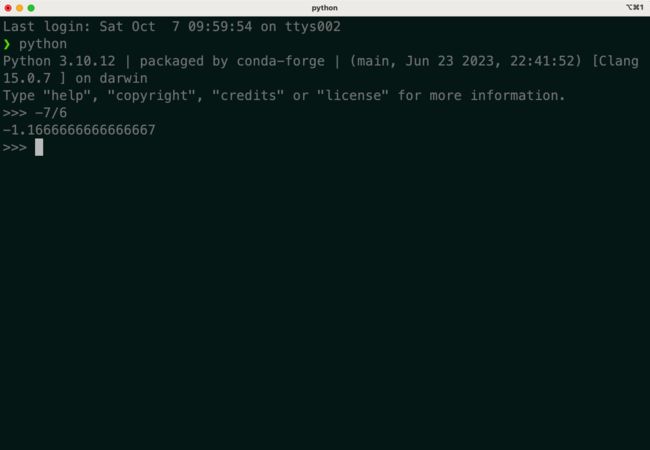
最后几次打印出的结果基本趋于一致了，k的值就是-1.1666，那数学里边我们学过，这个二次函数最优值应该是-b/2a，应该是-7/6，我们计算一下看看：

可以看到，和我们梯度下降所求的值很接近，几乎一致。

这个例子说明通过靠梯度下降，是能够找到一个变量让这个函数取得最小值。

既然咱们刚才面对这个问题能直接能计算出来它的值是-b/2a = -1.16666…, 为什么要用梯度下降的方法来得到这个不精确的值呢?

我们的这个例子是一个简单函数，可是当函数很复杂的时候，很多复杂的函数我们是求解不出来的。

好，到这里就是我们这节课的内容。下节课就是我们机器学习入门的最后一节课，我们来谈谈K-means。