【读书笔记】《数据压缩入门·上》——柯尔特·麦克安利斯

数据压缩入门汇总

读书笔记——数据压缩入门（柯尔特·麦克安利斯）上
读书笔记——数据压缩入门（柯尔特·麦克安利斯）中
读书笔记——数据压缩入门（柯尔特·麦克安利斯）下

前言

科研方向是数据管理方面，硬肝吧，这几天给它啃完；对了，是在微信读书上找到的，以后阅读也在上面搞，开个会员也不用到处找pdf；

第一章 概述

  数据压缩算法有5类：变长编码(variable-length codes，VLC）、统计压缩（statistical compression）、字典编码（dictionary encodings）、上下文模型（context modeling）和多上下文模型（multicontext modeling）；

  每类算法的变种在输入数据、算法性能、内存要求以及输出大小方面存在细微的差别。要选出其中最佳的一个算法，需要在准备的数据上测试这些算法，然后找出压缩效果最好的那个。

  每类算法的变种在输入数据、算法性能、内存要求以及输出大小方面存在细微的差别。要选出其中最佳的一个算法，需要在准备的数据上测试这些算法，然后找出压缩效果最好的那个。

  要学会如何搭配这些算法，得到能够满足你目标的混合算法；

1.1 克劳德 • 香农

  香农发明了一种度量消息所携带信息内容的方法，并称之为信息熵（informationentropy）；数据压缩其实是香农的研究工作的一项实际应用，它所研究的问题是，“在保证信息能恢复的前提下，我们能将消息变得多么紧凑”；
  可以把数据压缩看成对信息熵的挑战；计算机科学家所写的每一个数据压缩算法都是为了反驳香农的研究，使数据的压缩程度超过用香农发明的公式计算出来的信息熵。我们想方设法地去掉信息中每一个冗余的二进制位，想让它变得尽可能小，以突破香农所定义的熵的下限，从而达到对信息的全新层次的理解；

1.2 数据压缩必备知识

对数据进行压缩，通常有两个思路：

• 减少数据中不同符号的数量（即让“字母表”尽可能小）；
• 用更少的位数对更常见的符号进行编码（即最常见的“字母”所用的位数最少）。

实际运用时却复杂得多，不同类型的数据所适合的压缩算法也不同：

• 不同数据的处理方法不同，比如压缩一本书中的文字和压缩浮点型的数，其对应的算法就大不相同。
• 有些数据必须经过转换才能变得更容易压缩。
• 数据可能是偏态的。例如，夏天的整体气温偏高，也就是说高气温出现的频率比接近零度的气温出现的频率高很多。

关于数据压缩的历史：

• 声音压缩：20实际90年代，当时，WAV格式才是创建、存储和传输音频数据的主流格式。几乎所有人在用WAV格式，但它存在一个很严重的问题，那就是文件特别大。一首3分钟的歌曲，文件的大小就将近30 MB，下载要花费9分钟左右，更别提流式播放了；MP3格式出现之后，一首音频质量很好、3分钟左右的完整歌曲，文件大小只有1~3 MB；
• 图像压缩；
• 视频压缩：2001年YouTube视频信息的主流传输格式是MOV，这一格式不比将一系列JPG图像按顺序排列先进；因此，只加载网页就能观看视频的想法在当时实在是令人难以置信；
• 基因图谱：单个基因组序列就包含了大量的数据，仅仅是描述人类基因组成的数据就超过了14GB。这样的数据大小超出了大多数系统能处理的范围；研究人员发现，BWT是最有效的存储DNA信息的压缩格式，甚至无须解压就能对数据进行操作。到了2014年，研究人员通过将可扩展的云计算与主机之间的压缩数据传输结合起来；
• 压缩与经济：压缩后的文件会变得更小。这也就意味着，同样的数据传输所需的时间会变短，相应的费用也会减少。分发者的分发成本会降低，消费者的支出也会减少；

第二章 深入研究信息论

信息论：即从数学的角度研究如何利用符号序列、脉冲序列或其他形式对信息进行编码，以及信息能以多快的速度在计算机电路或者电信信道中传输；

  根据信息论的观点，一个数值所包含的信息内容等于，为了在一个集合中唯一地确定这个数值，需要做出的二选一（是/否）决定的次数。

熵：表示一个数所需要的最少二进制位数

  给定整数x，通过公式得到它用二进制表示所需的位数：$lb(x)=(log(x)/log(2))=lo{g}_2^x=表示一个数所需要的二进制位数$；

  从数学上来说，lb将产生一个浮点数，例如，lb(10) = 3.321。然而，从技术角度来说，由于现代的计算机硬件无法表示3.321个二进制位，因此我们必须对这个值向上取整，也就是使用向上取整函数，即ceil（或ceiling）函数 = $lo{g}_2(x)=ceil(log(x)/log(2))$；

  这又产生了另外一个问题，因为从技术上来说，如果一个数正好是2的幂，那么通过这一公式所得的结果要比实际需要的二进制位数小1；所以，对公式进行修改：$lo{g}_2(x)=ceil(log(x+1)/log(2))$；

  数值的LOG2表示形式虽然高效，但对于制造计算机元件的方式来说并不实用。这其中的问题在于，如果用最少的二进制位数来表示一个数，在解码相应的二进制字符串时会产生混乱（因为我们并不知道该数对应的LOG2长度），会与硬件的执行性能相冲突，两者不能兼顾。现代计算机采用了折中的方案，用固定长度的二进制位数来表示大小不同的整数；

第三章 突破熵

3.1 理解熵

  上一章中，香农大佬提出表示一个数所需的最少的二进制位数即为这个数的熵，那么对于一个集合，它的熵如何表示，他又提出以下公式：$H(S)=-{\sum }_{i=1}^n{p}_{i}lb(p_i)$；注意，熵的计算公式中使用的lb()是数学意义上的，与我们在第2章定义的LOG2()函数不同。因此,这里通过lb()计算出的结果不会向上取整，同时也允许该值为负；

下面放上求熵的计算过程：

3.2 熵的用处

  因为G=[A,B,B,C,C,C,D,D,D,D]的熵H(G）=1.8455，所以我们可以大致认为平均每个值用2个二进制位（通过向上取整运算获得）就可以对G进行编码，比如A->00，B->01，C->10，D->11；编码之后G的大小就是20个二进制位（更直接的计算就是 H(G) * len(G)）；

  因此，总结起来就是，为了使表示某个数据集所需的二进制位数最少，数据集中的每个符号平均所需的最小二进制位数就是熵；

3.3 理解概率

  从本质上来说，香农所定义的熵，是以一种倒排序的方式建立在数据流中每个符号出现概率的估算之上的。总的来说，一个符号出现得越频繁，它对整个数据集包含的信息内容的贡献就会越少，这看起来似乎完全违背直觉；

  但时常，我们感兴趣的事都是不频繁出现的事，比如去河边钓鱼，如果用0表示没有鱼，用1表示鱼上钩，那么你记录的信息里很容易出现这样的片段：0000000010000000001000000000001；

3.4 突破熵

  事实上，通过利用真实数据的两个性质，我们完全有可能将数据压缩得比熵定义的还要小；按照香农对熵的定义，他只考虑了符号出现的概率，完全没有考虑符号之间的排序。而对真实数据集来说，排序是一项基本的信息，符号之间的关系同样如此；

  例如，排好序的[1,2,3,4] 和没有排序的[4,1,2,3] 这两个集合，按照香农的定义，两者的熵相同，但是凭直觉我们就能发现，其中的一个集合包含了额外的排序信息。我们再来看一个元素为字母的例子，[Q,U,A,R,K] 和[K,R,U,Q,A] 这两个集合有相同的熵，但[Q,U,A,R,K] 这个集合表示的是英语中一个有意义的单词，而且字母的出现也有一定的规则，比如字母Q后面通常会跟着字母U；

  突破熵的关键在于，通过利用数据集的结构信息将其转换为一种新的表示形式，而这种新表示形式的熵比源信息的熵小；

3.4.1 增量编码

  元素递增的集合[0,1,2,3,4,5,6,7] 称为集合A；现在，打乱集合A中元素的顺序，得到集合B=[1,0,2,4,3,5,7,6]。根据信息论的观点，这两个集合具有如下独特的性质：

• 所有的符号都等可能地出现，并且没有重复的符号；
• 集合A和集合b的熵H相等，都等于 3；

  因此，根据香农的定义，每个符号都需要用3个二进制位来编码，而每个集合则需要24个二进制位。然而最终的结果是，我们很容易就能突破熵的限制，用更少的二进制位对集合A进行编码，具体方法如下：

  集合A实际上是数的一个线性递增序列。因此，无须对其中的每个数都进行编码，而是可以对整个数据流进行转换，将各个数编码为其与前一个数的差。所以，编码后的A会是这样：[0,1,1,1,1,1,1,1]，这一数据流的熵H(A)=1，这样的转换称为增量编码（delta coding），也就是将一系列的数转换为其与上一个数的差后再编码；

  下面来讨论集合B。由于B中的数并不是线性递增的，因此增量编码的方法不会起作用，这样操作之后我们会得到集合[1,–1,2,2,–1,2,2,–1]，其熵为2，乍一看这个结果还不错。然而，如果真的这样做，那么首先需要用16个二进制位将多重集合B，编码为[01,00,10,10,00,10,10,00]。此外，还需要告诉解码器编码“00”表示的是符号–1，这就需要额外的空间来存储。因此，即使能节省空间，也节省不了多少。实际上，对某些集合来说，与直接对数据进行编码相比，增量编码所需要的二进制位甚至要更多。

  根据熵的定义，符号之间的顺序无关紧要，但增量编码证明事实并非如此。如果相邻的值之间高度相关，那么用增量编码的方法可以转换数据，使其熵变得更小；

3.4.2 符号分组

  上述字符分组的例子表明，如果数据集中存在连续值组合出现多次的情况，就可以利用这种情况来减小熵。一般来说，通过最佳符号分组预处理数据，会得到一个较小的熵值；

3.4.3 排列

事实上，排列是可以稍微压缩的，但这个过程没什么意思，也没多少实际价值；


  无论排列的大小多大，这种方法都适用。通过这种方法来编码，总能确保最终所产生的数据流比通过熵计算的小。例如，如果你遇到的是包含从0到65535这些整数的一个排列，不管这些整数的顺序如何混乱，你总可以将这些数据压缩到原空间的90%。实际上，只节省这么少的空间通常不值得我们这样去做。

  解码工作则以相反的方式进行。最开始时，我们有一个空的数组，然后从数据流中读出LOG2（#没有赋值的元素个数）个二进制位，这表示的是该元素的下标，通过下标我们就知道它原来所代表的值。具体操作如下。

① 一共有8个没有赋值的元素，因此从输入流中读出前3个二进制位，这里是101。
② 二进制101对应的值为5，下标5对应的值为5，因此第一个数是5。现在，将5从数组中删除。
③ 还有7个没有值的元素，我们需要读取接下来的LOG2(7)（即3）个二进制位，其值为110，对应的十进制下标为6，本来它应该对应值6，但因为之前数值5删除了，因此这里6对应的值往后移一位，对应值7，即第二个数为7；
④还有六个没有值的元素，LOG2（6）=3，值为001，对应下标为1，因为目前1前面没有删除值，所以下标1对应值1，即第三个数为1；
⑤接下来，请按照上面的方法解码剩下的元素。

3.5 信息论与数据压缩

  需要记住的是，熵定义的只是在对数据流进行编码时，每个符号平均所需的最小二进制位数。这就意味着，有些符号需要的二进制位数比熵小，而有些符号需要的二进制位数则比熵大。

  数据压缩算法的艺术，就在于真正试图去突破熵的限定，或者说是将数据转换成一种熵值更小的、新的表现形式。这可以说是真正的舞蹈：信息论已经制定了相应的规则，数据压缩则以斗牛士的热情巧妙地避开了这些规则。

  正如前面所讨论的那样，在对压缩进行评价时熵不是一个好指标。其实，还存在其他更准确的度量复杂性的方法，但这些方法在使用上还没有真正地标准化。柯尔莫哥洛夫复杂性（Kolmogorov complexity），度量的是确定一个对象所需要的计算资源；

总结一下：

• 熵，指为了唯一地描述一段数据所需要做出的“是”“否”回答的次数。
• 柯尔莫哥洛夫复杂性，指为了准确地生成数据，所需要的生成程序的大小。
• 可以证明，任何字符串的柯尔莫哥洛夫复杂性顶多比字符串本身的长度大几个字节(基本上，也就是一个程序输出字符串的每个元素）。那些柯尔莫哥洛夫复杂性要比字符串本身小很多，就像上面的所举的abab的例子，可以认为这样的字符串都很简单。

  当开始讨论用逻辑综合（logic synthesis）或者程序综合（program synthesis）进行数据压缩的时候，柯尔莫哥洛夫复杂性就开始真正起作用了，本质上它取的是数据集以及反向生成产生字符串的程序的二进制位流。

  平心而论，这样的解释有些大而化之。熵远远算不上最佳解决方法，但它的确是很多人信任的“足够好的”度量标准。要找到一个更准确的解决方法，涉及对数据信息和分析空间的大量随机探索。这里，需要着重说明的是，虽然已有将近50年的历史，但是数据压缩作为一个学科仍然很年轻。不是所有的问题都有答案，而这才是你真正需要去努力探索的。

第四章 VLC变长编码

上一章举的例子说明两个问题：

• 一是可以通过用更少或更多的二进制位对某些符号编码来节省所需要的总空间；
• 二是当数据集中有重复符号时，这个方法就不太有用了。我们必须面对这个问题，因为在真实的数据集中，符号重复几乎无法避免；

  我们必须面对这个问题，因为在真实的数据集中，符号重复几乎无法避免。这就是为什么LOG2方法无法正确地表示一个数据集中所真正包含的信息内容。

  本章将展示怎样利用概率和重复来做一些漂亮的工作，最终产生让人印象深刻的压缩结果。

4.1 摩尔斯码

  我们都知道，在英语中有一些字母比另外一些字母使用得更频繁，比如字母E会在12% 的时间里用到，而字母G则只在2% 的时间里用到。如果操作人员每天发送的字母“E”更多，那么是不是应该让这样的操作变得更快、更简单呢？最终，摩尔斯码被发明出来。

  摩尔斯码为英语字母表中的每一个字符都分配了或长或短的脉冲，一个字母用得越频繁，其编码也就越短、越简单。因此，英语中最常用的字母“E”的编码最短，用一个点表示；而字母“X”的编码毫无疑问则很长；所有的数字都用5个脉冲表示。下图显示了摩尔斯码的原始字符集：

  19世纪对符号分配变长编码（variable-length codes，VLC）的最初实现目的在于减少传输信息过程中所需要的总工作量；

4.2 概率、熵和码字长度

  为了进行数据压缩，我们的目的很简单：给定一个数据集中的符号，将最短的编码分配给最可能出现的符号。不过我们还是暂时先退回来，看一看熵是如何与此相关的。假定一个大的数据集中只有[A,B] 两个符号，我们来计算一下每个符号出现的概率（也就是P（A）和P（B）），并看一看概率如何影响数据集的熵。下表展示了不同的样本概率与对应的数据集的熵：

观察这个表，可得出以下规律：

• 当P（A）=P（B），也就是两个符号等可能出现时，数据集对应的熵取最大值 LOG2（符号的个数），此时数据集很难压缩；
• 其中一个符号出现的可能越大，数据集的熵值就越小，此时数据集也越容易压缩。
• 对只包含两个符号的数据集来说，两个符号互换概率不影响其熵值，我们可以看到H(0.9,0.1)等于H(0.1,0.9)。

  首先，随着数据集的冗余度下降，它的熵在变大，其最大值为数据集中不同符号个数的LOG2值；例如，当数据集中有4个以相同概率出现的符号，其熵为–4(0.25lb(0.25)) = 2；也就是说，为了对每一个符号进行编码，平均来说至少需要2个二进制位；

  其次，数据集中一个符号出现的概率越大，整个数据集的熵就越小，数据集也就越容易压缩。 因此，作为对比，我们来考虑下表中包含4个符号且符号呈偏态分布的数据集，通过使用VLC，其熵仅为1.57。

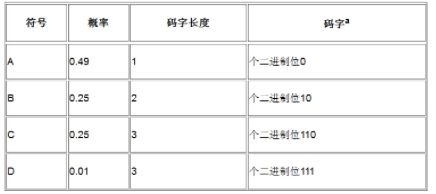
  这张表看起来很奇怪，不是吗？为什么不能用码字[0,1,00,10] 来对[A,B,C,D] 进行编码呢？这是因为前缀性质，这是解码的需要，同时也是构造编码时的一个基本要求；

  因此，对于给定的输入数据集，可先计算涉及的符号的出现概率，然后就可以通过VLC将字长最短的码字分配给最可能出现的符号，从而实现压缩数据。这真不错！当然，这里还存在两大问题没有解决。
第一，怎样在应用程序中运用VLC来进行压缩呢？
第二，对于给定的数据集，怎样构造VLC呢？

4.3 VLC

一般来说，对数据进行VLC通常有3个步骤：
(1) 遍历数据集中的所有符号并计算每个符号的出现概率。
(2) 根据概率为每个符号分配码字，一个符号出现的概率越大，所分配的码字就越短。
(3) 再次遍历数据集，对每一个符号进行编码，并将对应的码字输出到压缩后的数据流中。

下面来对每一个步骤进行一些讲解：
1.计算符号的概率
这个步骤包括画出数据集中所有符号的直方图。也就是说，我们需要遍历数据集，并计算出每个符号出现的次数，最终得到如图4-3所示的直方图，该图描述了每个符号与其出现次数（或者说频数）之间的对应关系；

2.为字符分配码字
接下来，根据出现的频数对直方图进行排序（见图4-4），然后给每个符号分配一个VLC，从VLC集中码字最短的开始。其结果就是，一个字符出现得越频繁，分配给它的码字就越短，如此就实现了数据压缩；

按照字符出现的频数对直方图进行排序之后，我们就能为字符分配码字。这张表通常也被称为“码字表”（codeword table）。注意，这里的码字并不表示标准的二进制数，这是编码和解码的需要（本章稍后会讨论这一内容）；
3.编码
用VLC的方法对数据流中的字符进行编码非常简单。只需要从数据流中一一读出各个符号，然后从码字表中查找出当前符号所对应的码字，添加到输出流中，再将所有的码字连接起来，就能得到最终的输出流。

处理完整个输入流之后，再将符号码字对应表添加到输出流的前面，如图4-5所示，这样解码的时候就能将输出流恢复为源数据。

该图展示的是一个编码示例，从输入流中读取一个符号，然后通过符号码字对应表查出相应的码字，再将码字添加到输出流中。所有的符号完成编码后，还要将符号码字对应表添加到输出流的前面，以方便后面的解码；
4.解码
一般来说，解码是编码的逆过程。如图4-6所示，解码时从输入流中读取二进制位，再通过符号码字对应表找出码字对应的符号，将此符号添加到输出流中。

  解码是编码的逆过程，从输入流中读取二进制位（也就是码字），再通过符号码字对应表找出码字对应的符号，然后输出这些符号；

  不过，由于码字的长度并非是固定的，因此解码过程还是稍微有些复杂。一般而言，解码的时候，我们会一二进制位一二进制位地读取数据，直到读取的二进制位流与其中的某个码字相匹配。一旦匹配，就会输出相应的符号，并继续读取下一个码字。我们来看看上一个例子中编码后所形成的二进制位流001101110111010001011100，并使用前述的符号码字对应表将它恢复为源字符串，步骤如下。

(1) 读取0
(2) 对照符号码字对应表，没有长为1个二进制位的码字
(3) 继续读取，还是0。对照符号码字对应表，00是码字，输出对应的符号T
(4) 读取下一个二进制位，即1
(5) 继续读取，还是1，在符号码字对应表找到码字11，输出对应的符号O。
现在，有意思的事情出现了
(1) 读取0，再读取下一个二进制位1。此时，我们发现对应表中有多个匹配，下一个字符可能是B、R或N。因此，需要继续读取第3个二进制位，得到“011”。现在，我们在表中找到唯一的一个匹配，字母B
(2) 按本书的惯例，剩下二进制位的解码由你来完成。当读到二进制位流的最后一位时，你应该已经恢复了源字符串（可以参考图4-7）。

  正因为如此，将摩尔斯码作为码字使用，其结果并不理想。所以，我们需要找到一种能将0和1放在一起，并且解码器能生成唯一输出流的方法。
  因此，在任意时刻，解码器都需要能确定到目前为止所读取的二进制位，是否与特定字符的码字相匹配，以及是否还需要继续读取下一个二进制位。为了确保正确，在设计VLC集的码字时，必须考虑两个原则：一是越频繁出现的符号，其对应的码字越短；二是码字需满足前缀性质。

VLC的前缀性质：在某个码字被分配给一个符号之后，其他的码字就不能用该码字作为前缀；

  前缀性质是VLC能正常工作所必须具有的性质。这也就意味着，与二进制表示相比，VLC要更长一些；下面提供几种方法解决前缀问题：

4.3.1一元码

  因此，将一元码应用在那些前一个符号的出现概率是后一个符号2倍的数据集上，效果最佳。（也就是说，A的出现概率是B的两倍，而B的出现概率又是C的两倍。）或者，如果你喜欢数学，我们可以说，对那些包含N个整数的数据集来说，如果每个整数n的出现概率p(n)服从指数分布2^-n，即1/2、1/4、1/8、1/16、1/32，其他以此类推，我们就可以使用一元码进行编码，比如：

  解一元码时，只需要从输入流中一直读取直到遇到分隔符0，然后数一下1的个数再加上1，最后将这个值输出就可以了；

4.3.2 Elias gamma编码

  lias gamma编码主要用于事先无法确定其上界的整数的编码，也就是说，不知道最大的整数会是多大。该方法最主要的思想是不再对整数直接编码，而是用其数量级作为前缀。这样一来，相应的码字就由两部分组成，即与此整数相当的2的次幂再加上余数，编码方法如下所示：

以42来举例：

与简单的一元编码类似，Elias gamma编码对那些整数n的出现概率P(n)=1/(2n²)的情形比较适用；

4.3.3 Elias delta编码

  Elias delta编码则是另外一个变种。在这一方法中，Elias还在前面加上了二进制的长度，使这一编码稍微复杂一些。

VLC变长编码的算法比较多，但有以下问题：

• 它们不按字节 / 字 / 整型对齐
• 对于大的数值n，为了方便解码，其码字长度的增长速度一般会超过lb(n)个二进制位
• 解码的速度很慢（每次只能读取一个二进制位）；

---

  对那些需要处理很多大整数的系统来说，这些问题使得VLC无法应用。然而，在21世纪初，出现了一个新的可变长度整数模型，在搜索引擎和其他海量数据系统中得到了广泛应用。它是以谷歌的Varint算法而流行的，在2010年作为“避免压缩整数”（escaping for compressed integers）而被重新引入。

  Varint是一种表示整数的方法，它用一个或多个字节来表示一个整数，数值越小用的字节数越少，数值越大用的字节数越多。该方法将几个字节连接起来表示整数，并用每个字节的MSB作为布尔标志，来判断当前的字节是否为该整数的最后一个字节；而每个字节的低7位则用来存储该数的二进制补码（two’scomplement representation）。下面就来看一些例子：

  整数1可以用一个字节表示，因此它的MSB不需要设置，可表示为00000001。再来看整数300，它的表示则要复杂一些：10101100 00000010。那么如何判断它表示的是300呢？
  首先，需要删掉每个字节的MSB，因为它的作用只是判断当前字节是否是最后一个字节（正如你看到的那样，第一个字节的MSB已经设置为1，因为用Varint方法来表示，该数需要多个字节）。10101100 00000010 → 0101100 0000010 ；

  接着，将剩下的两个7二进制位的数据顺序颠倒一下 -> 0000010 0101100，因为用Varint方法表示时，低位的字节在前。最后，将二进制表示转换为十进制数，就得到了最终的数值。

  Varint表示方法结合了VLC的灵活性和现代计算机体系结构的高效率，是一种很好的混合方法。它既允许我们表示可变范围内的整数，同时还对自身的数据进行了对齐以提高解码的效率，达到了双赢。

4.4 选择合适的编码方案

  前面介绍的各种编码方法的最大区别是，当给定符号的概率分布期望不同时，这些编码方法的表现也不同。

  因此，在为数据集选择一种VLC编码方法时，必须要先考虑数据集的整体大小和数据范围，并计算各个符号的出现概率。如果不这样做，得到的结果可能就是，数据集的大小不但没有压缩，有可能反而比原来的数据集还大。

  为了让你了解每种编码方法最终的结果差异，我们来看下表，它展示了在理想的概率设定下，符号总数相同时使用不同的方法，每个符号需要用多少二进制位来表示；

第五章 统计编码

  除了少数情形外，第4章中所讨论的那些VLC方法在数据压缩的主流领域中使用得并不多。正如第4章提到的那样，每种编码方法都对每个符号的概率分布做了不同的假定；

  统计编码（statistical encoders），这类算法无须将特定的整数转换为特定的码字，而是通过数据集中符号的出现概率来确定新的、唯一的变长码字。最终的结果就是，给定任何输入数据，我们都能为其构造出一套自定义的码字集，而无须去匹配现有的VLC方法。

  可以认为熵编码就是统计编码，早期，熵编码技术主要包括：霍夫曼编码和香农编码，后来国际电信联盟H.82建议书（ITU-T，1993）将熵编码定义为“任意无损的压缩或解压数据的方法“。

  我们用统计编码这一术语来定义如下的算法，该算法以数据流中符号的频率为依据，为该数据流中的各个符号分配长度可变的码字，从而使最终的输出压缩得更小。

5.1 哈夫曼编码

  哈夫曼编码可能是生成自定义VLC最直接、最有名的方法。给定一组符号及其出现频率，该方法能生成一组符号平均长度最短的VLC。它的工作原理是将数据排序后建立决策树(decision tree），然后从“树干”一直往下直到“树叶”为止，并记录下所做的是/否选择(几乎又回到了“20个问题”这个游戏上）。这里所说的“树叶”就是我们要找的各个符号；这个都比较熟悉，就不解释了；

5.2 算术编码

  事实上，哈夫曼编码能生成理想VLC（即码字的平均长度等于符号集的熵）的唯一情形是，各个符号的出现概率等于2的负整数次幂（即是1/2、1/4或1/8这样的值）。这是因为哈夫曼方法会为给定符号集中的每个符号都分配一个整数二进制位长的码字；

  信息论告诉我们，如果一个符号的出现概率为0.4，那么它最理想的码字长度应该是1.32个二进制位，因为–lb(0.4) ≈ 1.32。而哈夫曼方法分配给这个符号的码字长度则只能是1个二进制位或2个二进制位；

  这正是算术编码发挥作用的地方，与按照1∶1的比例为每个符号分配一个码字不同，算术编码算法会将整个输入流转换为一个长度很长的数值，而它的lb表示则与整个输入流真正的熵值很接近。

  事实上，现代主流的文件、音频和视频的压缩格式（如LZMA和BZIP这样的文件格式，JPEG、WebP、WebM和H.264这样的音视频格式），在统计编码步骤上都会使用算术编码压缩方法。
编码
下面举一个完整的编码例子，假定有3个字符R、G和B,其出现概率分别是0.4、0.5和0.1；



选出正确的值
  B的最终取值区间是[0.825,0.85)，在此区间内的任何数值都能让我们重新构建出原来的字符串，因此可以从中任取一值。由于本书讨论的是数据压缩，因此我们将尽可能选择可以用最少的二进制位来表示的数值（因而也尽可能与1.36个二进制位这个熵目标接近）。在这个取值范围内需要最少二进制位表示的数是0.83。最后，由于解码器事先“知道”这个数肯定是一个小数，因此可以去掉小数点以节省空间，将最终的值确定为83。由于lb(83) = 7，因此平均每个字符占用2.33个二进制位。
解码
就是个逆过程；

  对关注性能的人来说，上面用图例说明的解码过程可能并没有你希望的那么高性能。如果遇到1 MB大小的数据流，那么每次都需要将取值区间再细分为不同的符号数那么多份，如此一来则涉及很多的浮点数乘除运算；下面这个方法用来替代复杂的区间运算更为巧妙；

5.3 ANS非对称数字系统

  非对称数字系统（asymmetric numeral systems，ANS）。实际上，ANS是一种新的精确熵编码方法，所得到的结果可以和最优熵任意接近，它的压缩率与算术编码接近，而性能则与哈夫曼编码相当；

(1) 根据符号的出现频率对数值区间进行细分
(2) 创建一张表，将子区间与离散的整数值关联起来
(3) 每个符号都是通过读取和响应表中的数值来处理的
(4) 向输出流中写入可变的二进制位位数

这一算法独有的两个部分在第(2)步（子区间与整数值关联的表）和第(4)步（可变的二进制位位数）中。

这个备查表使得从符号转换为数值再从数值转换为符号成为可能，它是如何创建的？
创建这张表时，需要先根据符号出现概率的大小排序，每个符号作为表的一列，从左往右概率依次递减。

接下来需要往表中填入数值，这些数值需满足以下条件：

• 表中的每个值都是唯一的（即不存在重复）
• 每列都按照值从小到大排序
• 每行的值都要比该行的行号大

  如果能遵循这些原则，那么前面展示的编码/解码转换就都能正常工作，但是如果想要tANS变成真正的熵编码器，还必须要考虑以下两个性质：
(1) 在确定每一列值的个数时，需满足该值乘以maxVal后，等于该列符号的出现概率；
(2) 在确定每一行的值时，需确保该行列选择的值与该列符号的出现概率一致，这样当用该值除以行号，所得商就会（近似）等于该列符号的出现概率。

  第一个性质比较简单。这张表中最大的值maxVal=31。为满足前面所述的性质，我们需要将maxVal细分，并将P(S)XmaxVal个值分配给各个列。具体到前面所举的例子，有如下计算：

• 符号 B的出现概率P(B)=0.35，因此 B列会有 floor(0.35×31) = 10个值出现
• 符号 C进行同样的处理，因此 C列会有 6个值（0.2×31 = 6）
• 最可能出现的符号，也就是最左边的 A列，一共有P(A) x maxVal + 1行，这是因为 A列还需要为 maxVal 增加额外的一行；
  
  
  如何选择合适的maxVal值？
    假定需要处理的数据集中有28个不同的符号，那么最低限度下需要LOG2(28)= 5个二进制位的空间大小，这样一来，maxVal的值就等于2⁵-1=31。

5.4 实际中如何选择压缩算法

  因为计算机变得越来越快（并且算术压缩的专利已经到期），所以算术压缩已成为目前的主流算法。它不仅应用在大多数的多媒体编码器中，甚至有了有效的硬件实现；

  但ANS改变了一切。虽然它在数据压缩领域里出现的时间还不长，但是已开始取代过去20多年里占据主流地位的哈夫曼编码和算术编码。

  例如，ZHuff、LZTurbo、LZA、Oodle和LZNA这些压缩工具已开始使用ANS。鉴于其速度和性能，ANS成为主要的编码方法似乎只是时间问题。实际上，在2013年，这一算法又出现了一个被称为有限状态熵（Finite State Entropy，FSE）的更注重性能的版本，它只使用加法、掩码和移位运算，使ANS对开发人员更具吸引力。它的性能是如此强大，以至于2015年推出了一款名为LZFSE的GZIP变种，作为苹果下一代iOS版本的核心API。

  目前看来未来的路似乎很清楚：ANS和FSE将终结哈夫曼编码和算术编码在压缩领域内几十年的“霸主”地位。