【排序】快速排序及其非递归实现，归并排序详解

快速排序

　　快速排序（Quicksort）是对冒泡排序的一种改进。
　　我们知道快速排序用的是分治的基本思想：将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归的解决这些子问题，然后将这些子问题的解组合为原问题的解。
　　快速排序的基本思想是：

　　通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

快速排序的基本思想用分治法可描述为：

• 分解：将一个序列以一个基准值分解为两个部分，一个部分所有值都比基准值小，另一个部分所有值都比基准值大
• 求解：通过递归调用快速排序单趟排序算法对左右子区间进行单趟排序
• 组合：当求解步骤中的两个递归调用结束时，其左右两个子区间已有序。

　　快速排序的过程如下图：
　　

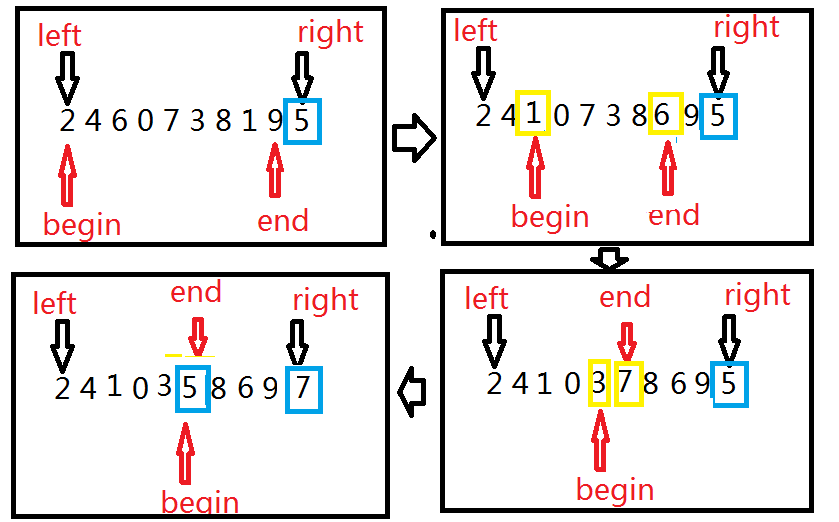
• 首先先找到最右边元素key = a[right]，将key作为基准值，单趟排序后所有key左边的数全部小于key，右边的数全部大于key。
• 从begin=left，end=right-1两个方向开始找，begin索引找的是比key大的数字，因为要找到比key大的数字然后与后面比key小的数字交换。
• 在begin小于end的前提条件下，只要begin找到比key大的数字，end找到比key小的数字，就交换两个值，然后继续寻找。begin++，end–

• 当begin小于end不成立，即begin==end时，判断a[begin]与key两个值，如果a[begin]>key，那么交换两个值。

  上面判断a[begin]>key的目的是：当一个数组只有两个数字的时候，如果不进行判断，会多一次交换。

  　　上面的过程有些抽象，现在放上代码：
  　　

int PartSort(int* a, int left, int right)
{
    int key = a[right];

    int begin = left;
    int end = right-1;

    while (begin < end)
    {
        // 找大
        while (begin < end && a[begin] <= key)
            ++begin;

        // 找小
        while (begin < end && a[end] >= key)
            --end;

        if (begin < end)
            swap(a[begin], a[end]);
    }

    if (a[begin] > a[right])
    {
        swap(a[begin], a[right]);
        return begin;
    }
    else
    {
        return right;
    }
}

现在来分析一下只有两个值的时候：

int a[2]={4,3};

　　此时left = 0,right = 1;key = a[right] ;
　　begin = 0;end = 0;
　　所以一开始begin < end条件就不成立,直接跳出循环，判断a[begin]与key的大小，得a[begin]>key，swap即可。
　　排序成功。

那么现在分析一下有序序列：

int a[2]={3,4};

　　此时left = 0,right = 1;key = a[right] ;key==4
　　begin = 0;end = 0;
　　所以一开始begin < end条件就不成立,直接跳出循环，判断a[begin]与key的大小，得a[begin] < key，不进行swap直接return。
　　排序成功。

　　上面只是单趟排序的算法。
整体排序算法：

void QuickSort(int* a, int left, int right)
{
    assert(a);

    if (left >= right)
        return;

    if(right - left < 50)
    {
        InsertSort(a+left, right-left+1);
        return;
    }

    int div = PartSort(a, left, right);
    QuickSort(a, left, div-1);
    QuickSort(a, div+1, right);
}


void TestQuickSort()
{
    //int a[] = {5,5,4,2,3,6,8,5,1,5};
    //int a[] = {9,0,4,2,3,6,8,7,1,5};
    int a[] = {0,1,2,3,4,5,6,7,8,9};

    QuickSort(a, 0, sizeof(a)/sizeof(a[0])-1);
    PrintArray(a, sizeof(a)/sizeof(a[0]));
}

　　上面的快速排序对其进行了优化，在数量小于50的情况下，其实用直接插入排序效果更好一些。

单趟排序方法2——挖坑法

　　挖坑法是快速排序单趟排序第二种方法：
　　我们设定end下标是一个坑，当begin找到比key值大的数的时候，将该值放入坑内，接着下一个坑就是begin下标所在位置，再从end开始往前找，找比key值小的数字，当找到后，再将值放入begin坑内，此时将坑变为end所在下标，直到begin小于end条件不成立为止。
　　
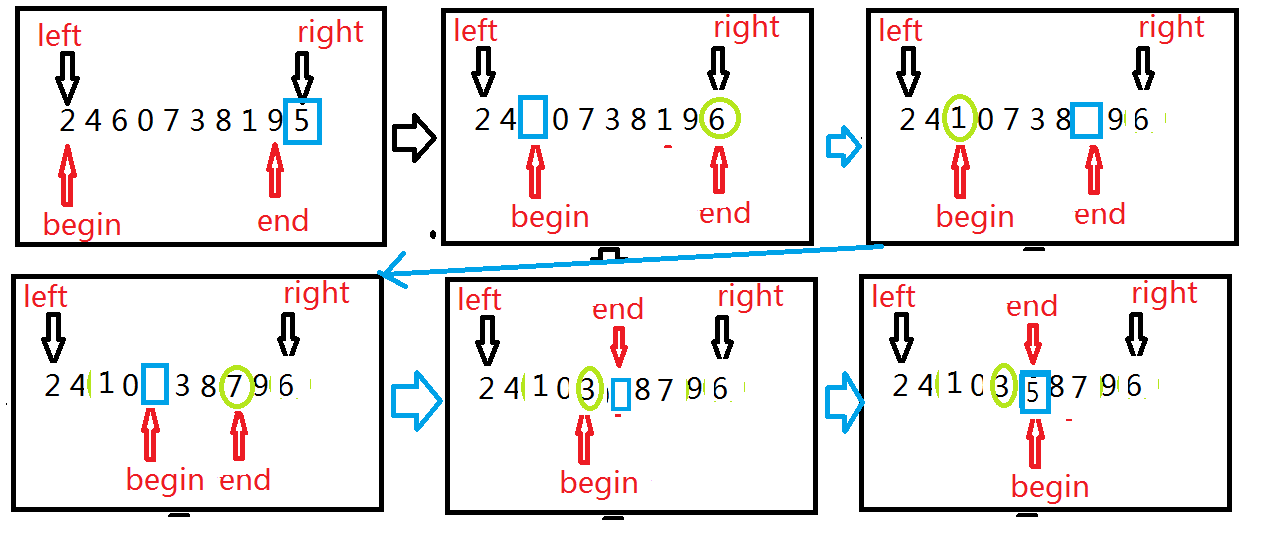
　　上图中，蓝色方框代表坑，绿色圆圈代表改变的数据。
　　代码为：
　　

// 挖坑法
int PartSort(int* a, int left, int right)
{
    int key = a[right];

    int begin = left;
    int end = right;

    while (begin < end)
    {
        while(begin < end && a[begin] <= key)
            ++begin;

        if (begin < end)
            a[end] = a[begin];

        while (begin < end && a[end] >= key)
            --end;

        if (begin < end)
            a[begin] = a[end];
    }

    a[begin] = key;

    return begin;
}

快速排序非递归实现

利用栈进行非递归存放数据。
代码如下：

#include 

void QuickSort_NonR(int* a, int left, int right)
{
    stack<int> s;
    s.push(right);
    s.push(left);

    while (!s.empty())
    {
        int begin = s.top();
        s.pop();
        int end = s.top();
        s.pop();

        int div = PartSort2(a, begin, end);

        // [begin div-1] [div+1, end] 
        if (begin < div-1)
        {
            s.push(div-1);
            s.push(begin);
        }

        if (div+1 < end)
        {
            s.push(end);
            s.push(div+1);
        }
    }
}

归并排序

　　归并排序是利用归并技术来进行排序。
　　归并是指将若干个已排序的子文件合并成一个有序的文件。
　　两路归并算法的基本思路：

归并过程为：比较a[i]和a[j]的大小，若a[i]≤a[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；否则将第二个有序表中的元素a[j]复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。

　　归并排序有两种实现方法：自底向上和自顶向下

自底向上

基本思想：

• 第一趟归并排序时，将待排序的文件A[1…n]看做n个长度为1的有序子文件，将这些子文件两两归并。若n为偶数，则得到n/2个长度为2的有序子文件，若n为奇数，则最后一个子文件不参与归并。
• 将前面的子文件两两归并，如此反复。

自顶向下

• 分解：将当前区间一分为二，即求分裂点
• 求解：递归的对两个子区间进行归并排序
• 组合：将已排序的两个子区间归并为一个有序的区间
• 递归终结条件：子区间长度为1

实现：

代码如下：

void _Merge(int* a, int* tmp
            ,int begin1, int end1
            ,int begin2, int end2)
{
    int index = begin1;
    while (begin1 <= end1 && begin2 <= end2)
    {
        if (a[begin1] < a[begin2])
            tmp[index++] = a[begin1++];
        else
            tmp[index++] = a[begin2++];
    }

    while(begin1 <= end1)
        tmp[index++] = a[begin1++];

    while (begin2 <= end2)
        tmp[index++] = a[begin2++];
}

void _MergeSort(int* a, int* tmp, int left, int right)
{
    if (left < right)
    {
        int mid = left+(right-left)/2;

        // [left, mid] [mid, right]
        _MergeSort(a, tmp, left, mid);
        _MergeSort(a, tmp, mid+1, right);

        _Merge(a, tmp, left, mid, mid+1, right);
        memcpy(a+left, tmp+left, sizeof(int)*(right-left+1));
    }
}

void MergeSort(int* a, size_t n)
{
    assert(a);

    int* tmp = new int[n];

    _MergeSort(a, tmp, 0, n-1);

    delete [] tmp;
}

void TestMergeSort()
{
    //int a[] = {5,5,4,2,3,6,8,5,1,5};
    int a[] = {9,0,4,2,3,6,8,7,1,5};
    //int a[] = {0,1,2,3,4,5,6,7,8,9};

    MergeSort(a, sizeof(a)/sizeof(a[0]));
    PrintArray(a, sizeof(a)/sizeof(a[0]));
}