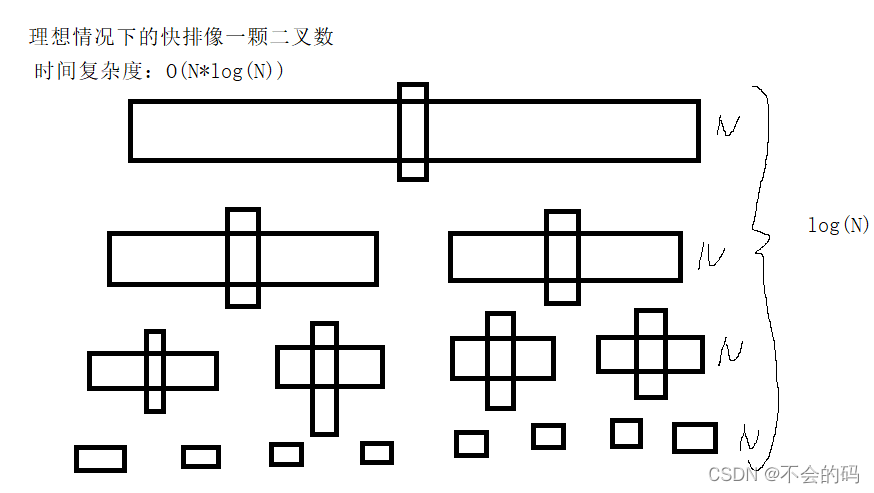
详解快速排序（递归）和非递归

目录

快排递归

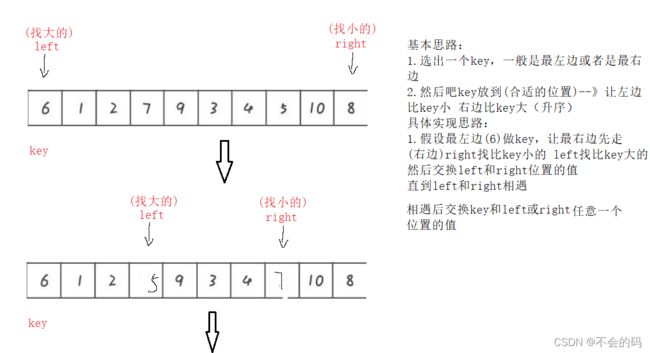
快速排序hoareba版(左右指针法)

思路：

注意 

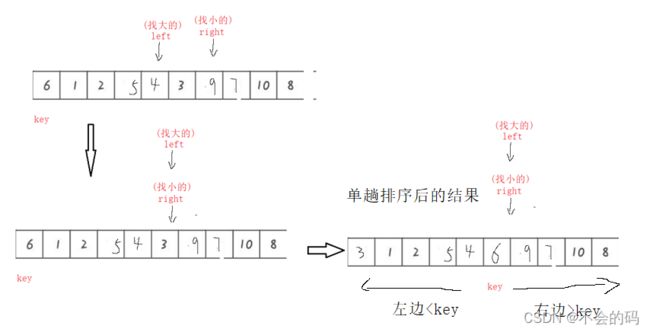
单趟实现代码

 多趟（递归）

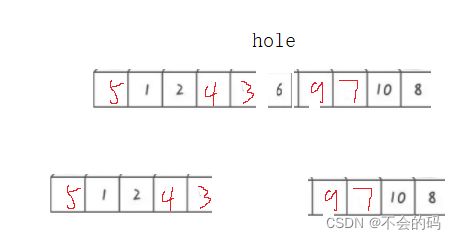
快速排序挖坑法

思路

 单趟实现代码

 多趟（递归）

 快速排序前后指针法

思路

​单趟实现代码

 多趟（递归）​

 非递归

 栈的实现

 非递归代码实现

极端情况下的快排及优化

 优化

三数取中代码

小区间优化

---

快排递归

快速排序hoareba版(左右指针法)

思路：

 

注意 

 左边做key,可以让左边先走吗？

不可以

左边做key必须让右边先走，右边(right)是找比key小的，找到小的停下来，即使相遇也能保证right位置的值小于key的

单趟实现代码

基于上面的思路可以先实现hoare的单趟排序

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
//快排hoare版 单趟
void QuickSort(int* a,int begin ,int end){

	//选左边做Key ,让右边先走
	int Key = left;
	while (left < right)
	{
		//right可能越界 当为1，2，3，4，5……10，right可能越界
		//找小
		while (left < right && a[right] >= a[Key])
		{
			right--;
		}
		//找大
		while (left < right && a[left] <= a[Key])
		{
			left++;
		}
       //找到后交换
		Swap(&a[left],&a[right]);
	}
  //相遇后交换key位置的值
	Swap(&a[left], &a[Key]);
}

 多趟（递归）

单趟排序后可以得到如下结果，然后在继续重复(递归)单趟排序

 直到只有一个(数)区间就停止递归

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

//快排递归
void QuickSort(int* a,int begin ,int end){
  //递归结束的条件
	if (begin >= end)
		return;
	int left = begin, right = end;
	//选左边做Key ,让右边先走
	int Key = left;
	while (left < right)
	{
		//right可能越界 当为1，2，3，4，5……10，right可能越界
		//找小
		while (left < right && a[right] >= a[Key])
		{
			right--;
		}
		//找大
		while (left < right && a[left] <= a[Key])
		{
			left++;
		}
		Swap(&a[left],&a[right]);
	}
	Swap(&a[left], &a[Key]);

	//找到相遇的
	//int meeti = left;
    //在递归这两个区间
	//[begin,metti-1] metti [metti+1,end]
	QuickSort(a,begin,left-1);
	QuickSort(a,left+1,end);
}

快速排序挖坑法

思路

 

 单趟实现代码

void QuickSort(int* a, int left, int right)
{
	int Hole = a[left];
	while (left < right)
	{
		//找小
		while (left < right && a[right] >= Hole)
			right--;
		//找到后把right的值放到坑里，左边成为新的坑
		a[left] = a[right];
		//找大
		while (left < right && a[left] <= Hole)
			left++;
		//找到后把left的值放到坑里，右边成为新的坑
		a[right] = a[left];
	}
	//相遇后填坑
	 a[left] = Hole;
}

 多趟（递归）

和前面Hoare递归非常类似 递归左边和右边

 

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	int begin = left,end = right;

	int Hole = a[left];
	while (left < right)
	{
		//找小
		while (left < right && a[right] >= Hole)
			right--;
		//找到后把right的值放到坑里，左边成为新的坑
		a[left] = a[right];
		//找大
		while (left < right && a[left] <= Hole)
			left++;
		//找到后把left的值放到坑里，右边成为新的坑
		a[right] = a[left];
	}
	//相遇后填坑
	 a[left] = Hole;
		//int meeti = left;
	//[left,metti-1] metti [metti+1,right]
	QuickSort(a, begin, left - 1);
	QuickSort(a, left + 1, end);
}

 快速排序前后指针法

思路

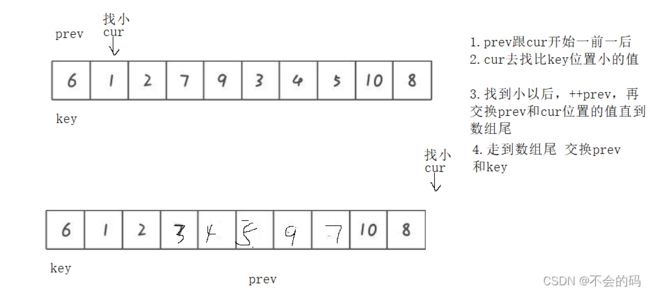单趟实现代码

 

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void QuickSort(int* a, int left, int right)
{
	int keyi = left;
	int prev = left, cur = left + 1;
	while (cur <= right)
	{
		//找小
		if (a[cur] < a[keyi])
		{
			++prev;
			Swap(&a[cur],&a[prev]);
		}
		cur++;
	}
	Swap(&a[prev],&a[keyi]);
}

 多趟（递归）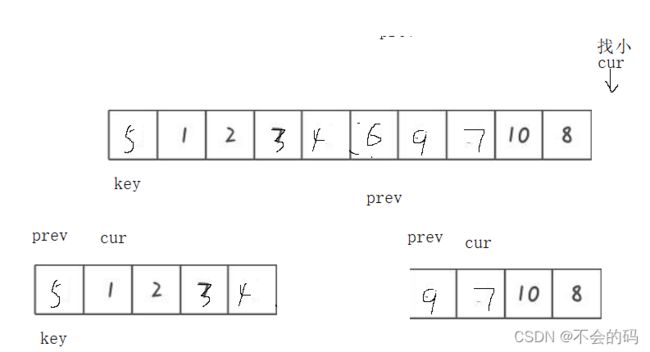

 

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	int keyi = left;
	int prev = left, cur = left + 1;
	while (cur <= right)
	{
		//找小
		if (a[cur] < a[keyi])
		{
			++prev;
			Swap(&a[cur],&a[prev]);
		}
		cur++;
	}
	Swap(&a[prev],&a[keyi]);
	//[left,prev-1] prev [prev+1,end]
	QuickSort(a,left,prev-1);
	QuickSort(a, prev+1, right);
}

 非递归

 使用栈来实现非递归，本质上是用栈来模拟递归过程

 栈的实现

Stack.h

#include
#include
#include
#include


//stack 堆栈
typedef int STDateType;
typedef struct Stack
{
	STDateType* a;
	int top;//栈顶
	int capacity;//容量
}Stack;

//初始化
void StackInit(Stack* ps);
//销毁
void StackDestroy(Stack* ps);
//入栈
void StackPush(Stack* ps, STDateType x);
//出栈
void StackPop(Stack* ps);

//获取栈顶元素
STDateType StackTop(Stack* ps);

//空返回1，非空返回0
//int StackEmpty(Stack* ps);
bool StackEmpty(Stack* ps);
int StackSize(Stack* ps);

 Stack.c

#include"Stack.h"


void StackInit(Stack* ps)
{
	    assert(ps);
		STDateType* p = (STDateType*)malloc(sizeof(STDateType));
	  if (p == NULL)
	  {  
		  printf("fail of Stack malloc");
			  exit(-1);//结束整个程序
	  }
	  else
	  {
		  ps->a = p;
		  ps->capacity = 1;
		  ps->top = 0;
	  }
}
void StackDestroy(Stack* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}

//void StackIncre(Stack* ps)
//{
//	//需要增容
//	if (ps->top == ps->capacity)
//	{
//		STDateType* p = (STDateType*)realloc(ps->a ,sizeof(STDateType)*(ps->capacity));
//		if (p == NULL)
//		{
//			 printf("fail of Stack relloc");
//			 exit(-1);//结束整个程序
//		}
//		else
//		{
//			ps->a = p;
//			//ps->capacity *= 2;
//		}
//	}
//}
void StackPush(Stack* ps, STDateType x)
{
	//StackIncre(ps);
	if (ps->top == ps->capacity)
	{
			STDateType* p = (STDateType*)realloc(ps->a ,sizeof(STDateType)*(ps->capacity)*2);
			if (p == NULL)
			{
				 printf("fail of Stack relloc");
				 exit(-1);//结束整个程序
			}
				ps->a = p;
				ps->capacity *= 2;
	}
	ps->a[ps->top] = x;
	(ps->top)++;
}
void StackPop(Stack* ps)
{ 
	assert(ps);
	assert(!StackEmpty(ps));
	ps->top--;
}
STDateType StackTop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));

	return ps->a[ps->top-1];
}
bool StackEmpty(Stack* ps)
{
	assert(ps);

	return ps->top == 0;
}
int StackSize(Stack* ps)
{
	assert(ps);
	return ps->top;

}

 非递归代码实现

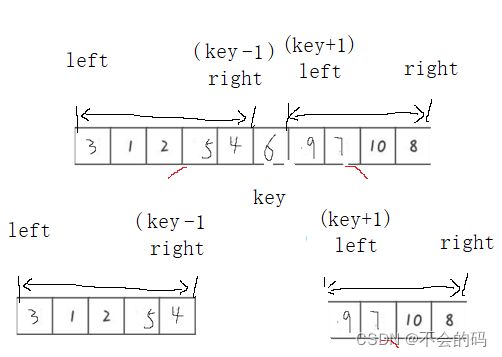
借鉴前面的思路，找一个key,让其左边比它小，右边比他大，然后在递归下去

假如左边做key，右边就要先走，那么利用栈 后进先出 的特点，先入左边，再入右边；先出右，再出左，然后在调用前面单趟排序的函数，使的左边比key小，右边比key大

 

//[left,key-1] key [key+1,right]

然后在入左边的区间（先入left，再入right(key-1)），入右边的区间(先入left(key+1),再入right);

//单趟排序选出key合适的位置
int PartSort1(int* a, int left, int right)
{
	//选左边做Key ,让右边先走
	int Key = left;
	while (left < right)
	{
		//right可能越界 当为1，2，3，4，5……10，right可能越界
		//找小
		while (left < right && a[right] >= a[Key])
		{
			right--;
		}
		//找大
		while (left < right && a[left] <= a[Key])
		{
			left++;
		}
		Swap(&a[left],&a[right]);
	}
	Swap(&a[left], &a[Key]);
//返回相遇的位置
	return left;
}
void QuickSortNonR(int* a, int left, int right)
{
	Stack st;
    StackInit(&st);
	//入左 再入右
	StackPush(&st, left);
	StackPush(&st, right);
	//不为空往里面入数据
	while (!StackEmpty(&st))
	{
		//先出右 再出左
		int left, right;
		right = StackTop(&st);
		StackPop(&st);

		left = StackTop(&st);
		StackPop(&st);
        //前面的单趟排序找到key合适的位置
		int keyi = PartSort1(a,left,right);
        //先入左边的区间
		if (left < keyi - 1)
		{
			StackPush(&st, left);
			StackPush(&st, keyi - 1);
		}
       //再入右边的区间
		if (keyi + 1 < right)
		{
			StackPush(&st, keyi + 1);
			StackPush(&st, right);
       	}
	}
	StackDestroy(&st);
}

极端情况下的快排及优化

 

 

 优化

三数取中：三个数里面取中间值做key,这样key不为最大或者最小

三数取中代码

//优化 三数取中
int GetMindDate(int* a, int left, int right)
{
	//移位操作符
	int mid = (left + right) >> 1;
	//int mid = (left + right)/2;
    //左边，中间，右边三个数比较取中间值
	//left mid right
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		//mid > a[right]
		else if (a[left] > a[right])
		{
			return right;
		}
		else//(a[left] < a[right]
		{
			return left;
		}
	}
	else //a[left] > a[mid]
	{
		if (a[right] < a[mid])
		{
			return right;
		}
		//a[right] > a[mid]
		else if (a[left] > a[right])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
}

 优化后

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

//快排递归
void QuickSort(int* a,int begin ,int end){
  //三数取中
	int mind = GetMindDate(a, left, right);
//保持左边做key
	Swap(&a[mind], &a[left]);
  //递归结束的条件
	if (begin >= end)
		return;
	int left = begin, right = end;
	//选左边做Key ,让右边先走
	int Key = left;
	while (left < right)
	{
		//right可能越界 当为1，2，3，4，5……10，right可能越界
		//找小
		while (left < right && a[right] >= a[Key])
		{
			right--;
		}
		//找大
		while (left < right && a[left] <= a[Key])
		{
			left++;
		}
		Swap(&a[left],&a[right]);
	}
	Swap(&a[left], &a[Key]);

	//找到相遇的
	//int meeti = left;
    //在递归这两个区间
	//[begin,metti-1] metti [metti+1,end]
	QuickSort(a,begin,left-1);
	QuickSort(a,left+1,end);
}

小区间优化

减少递归数的最后几层，使用插入排序

 1、如果这个子区间是数据较多，继续选key单趟，分割子区间分治递归

2、如果这个子区间是数据较小，再去分治递归不太划算，使用插入排序

//插入排序
void InsertSort(int* a, int n)
{
	//多趟排序确定 end，tmp的位置
	for (int i = 0; i< n - 1; i++)
	{
		int end = i;
		int tmp = a[end + 1];

		//单趟插入，在有序区间[0,end]之间插入tmp
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				 a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}

		}
		//出循环可能是循环结束 也可能是Break的 注意tmp为0时一直比他们小
		a[end+1] = tmp;
	}
}
void QuickSort(int* a, int begin, int end) {
    //优化
	//三数取中
	int mind = GetMindDate(a, begin, end);
	//保持左边做key
	Swap(&a[mind], &a[begin]);
	//递归结束的条件
	if (begin >= end)
		return;
     //优化
	//子区间较大时选Key单趟排序 递归
	if (end - begin > 20)
	{
		int left = begin, right = end;
		//选左边做Key ,让右边先走
		int Key = left;
		while (left < right)
		{
			//right可能越界 当为1，2，3，4，5……10，right可能越界
			//找小
			while (left < right && a[right] >= a[Key])
			{
				right--;
			}
			//找大
			while (left < right && a[left] <= a[Key])
			{
				left++;
			}
			Swap(&a[left], &a[right]);
		}
		Swap(&a[left], &a[Key]);

		//找到相遇的
		//int meeti = left;
		//在递归这两个区间
		//[begin,metti-1] metti [metti+1,end]
		QuickSort(a, begin, left - 1);
		QuickSort(a, left + 1, end);
	}
	else //子区间数据较小 选用插入排序
	{            //因为有很多的子区间，前面传参要加上begin,后面传参表示子区间数据个数
				InsertSort(a + begin, end - begin + 1);
	}
}