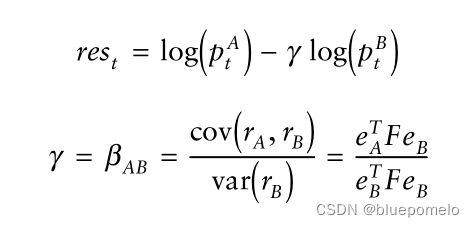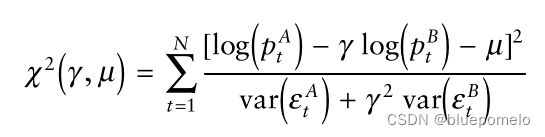可交易性（tradability)检验即协整性检验：线性关系

两个时间序列的线性关系表示为：

 左边是两个时间序列的线性组合。是协整系数。

右边是残差序列（residual series),表示为由两部分组成。是均衡值（equilibrium value），是一个均值为0的时间序列，可以构造为均衡值的波动项。如果时间序列是均值回归的，那就是围绕着均衡值波动。所以，两时间序列的线性关系又称为均衡关系，由两个参数描述以及。

现在我们来看一个例子：一个长短投资组合，买入1份A,卖出份B。代表持有股票A所支付的溢价超过股票B的同等头寸。现实生活中是否存在这样的溢价？事实上，由于各种原因，股票确实溢价交易。更大的相对流动性（流动性溢价），公司成为收购目标的可能性（收购溢价），以及一些股票的纯粹魅力，这些都可能是一些原因。

---

估计线性关系的方法之一：多因子方法

需要注意的是，协整系数的计算设计两个值，这取决于自变量的选择。如果线性关系是假设股票B是自变量来表示的，我们有：

 如果假设股票A是自变量的话，则有：

 

 和我们该用哪个值呢？建议使用两者间较大的那个。一种解释就是，比如当时，,我们选择较大的协整系数，则选择了具有较小波动率的股票作为自变量。

一旦确定了协整系数，我们很容易估计残差时间序列（residual time series)，而正是残差时间序列的均值。如果这个均值与零有显著差异，那么我们就有非零的均衡值。否则，我们认为均衡值是零。

总结估计均衡关系的步骤：

---

估计线性关系的方法之一：回归的方法

如果两个时间序列是协整的，那么回归方程的斜率即协整系数，截距即溢价（premium) 。

回归的方法优点就是简单，但是正因如此，更加要去了解标准回归场景（standard regression scenario)以及偏离这种标准场景的情况。因此，让我们看看应用于物理系统的标准回归场景。物理系统的核心是因果关系的研究；即系统对特定刺激的响应。如果期望的是响应与刺激成比例，那么线性回归过程在估计这个比例常数时非常方便。典型的实验包括使系统经受一系列输入或特定范围内的刺激，并测量系统对这些输入的响应。然后，输入输出对形成用于线性回归的数据集。在这种情况下，自变量是输入或刺激，回归方程的斜率表示刺激和响应的比例常数。

现在让我们重点看一下实验过程的一些方面。注意，在这种情况下，由于实验者是管理着系统的输入，所以他或她可以将输入设计得非常精确的，误差非常小。因此，我们可以假设输入数据中没有误差。然而，输出数据来自系统的响应，由于实验条件不完善，我们可能无法准确知道这个输出数据。此外，如果实验条件在试验过程中没有发生显著变化，我们可以假设每次响应观察到的数据的误差是来自共同的概率分布。因此，在这种情况下，输入是相对准确的，误差源仅在输出中，而且输出的误差标准差在所有观察中是固定的。

现在把股票价格数据与以上场景联系在一起。有人会说，股价不是明确可知的吗，怎么存在误差？需要知道的是我们只是知道某个时间周期的代表价格，而实际上在一个时间周期中价格是变动的。因此，对于我们在该时间段内选择的价格存在不确定性或误差。在我们的股价场景中，因果之间（自变量和因变量）没有明显的界线，两种股票的价格很可能相互影响。由于在这种情况下不可能轻易地将因果关系分开，而且两个股票的价格都可以被视为输出，因此我们现在面临着两个变量都可能存在不确定性或有误差的情况。这与标准线性回归场景有很大不同，后者只假设一个变量中存在误差。

再股票场景中，两个观测值（两个股票价格变量）都存在误差，观测误差的方差也是一个变化的量。尽管我们的情况与标准回归场景有很大的差异，但这绝不是什么新鲜事。在其他应用中也会遇到这样的问题。非恒定误差分布以及两个变量中的误差的情况可以通过最小化以下的chi-squared merit 卡方价值函数来处理:

 以及表示观测值以及误差的方差。假设误差具有零平均值，并可在每个时间段内根据股票的走势范围（range of movement)进行校准。注意，对误差方差的绝对度量并不重要，只要这个值与实际方差成比例即可。

让我们进一步了解卡方函数如何处理非恒定误差分布的情况。如果，式子中的分母是个常数，那么最小化的问题就变成了最小化分子，即最小化误差平方和。而分母变成了一种权重。这种使用卡方价值函数进行回归的方法有时也称为加权最小二乘法。

然而，采用加权最小二乘法的典型应用仅假设因变量中的误差，而不是两种变量（自变量和因变量）中的误差。具体来说，这些应用中的分母中没有项。分母中这个项的存在使卡方函数的最小化变得复杂，因为卡方函数关于的导数是非线性的，因此我们可能需要求助于数值方法来解决这个问题。总之，如果我们要考虑测量中变化的误差概率分布以及两个变量的测量误差，回归过程可能会相当复杂。

然而，如果有一种方法可以构造价格序列，使得这个序列每个时间段中与观测相关的误差可以假设为相同，那么我们可以消除这些复杂性，只使用普通的最小二乘法，并得出合理的答案。让我们看看我们是否能够做到这一点。

在给定的时间段内，我们只从该段时间内的股价变动范围中选择一个代表性价格。在周期长度为一个交易日的典型场景中，构建每日时间序列的标准惯例是使用的代表价格是交易日结束时的收盘价；即价格时序中最新的价格。让我们将这种记录价格时间序列的方法称为收盘法(close-close method)。这个方法是否适用我们的场景？习惯性地使用相同的方法而不管其目的是什么，这是很有诱惑力的，尽管这样的做法可能是不明智的。必须注意确保数据构建过程反映了当前的具体目的。

我们的目的是研究两种股票之间的价格关系。在这项研究中，为了检验价格关系，比给定时间段内的收盘价更重要的是对“在该时间段内，流动性的最大价格是多少？”这一问题的答案。这将是大多数买家和卖家一致认为价格合理且大量股票易手的时间段内的共识价格（consensus price)。因此，使用两种股票的最大流动性价格序列得出的结论将比使用收盘法可靠得多。这种价格即 the volume weighted average price交易量加权平均价格VWAP。我们使用VWAP去构建时间序列。

通过使用VWAP价格，我们有理由假设无论价格范围的大小，从最大流动性价格得到的VWAP价格的误差分布大致相同。因此，我们可以在回归分析中使用简单的普通最小二乘法。当然，构成t统计检验基础的标准误差计算方式仍需改变。在我们的协整检验或者可交易性检验场景中，对t统计的重视程度相当低，因此我们认为这是我们可以接受的。此外，请注意，使用VWAP价格有缓和极端值的作用，因此具有最小化异常值对回归的影响的额外好处。总之，用VWAP价格构建的时间序列更适合理解均衡价格关系，应该是首选方法。

 然而，这并不意味着能够决定我们应该使用两个价格序列中的哪一个作为自变量。这里采用跟多因子模型案例中相同的想法。