泛函分析（二）巴纳赫（Banach）不动点，贝尔曼方程（Bellman equation）在强化学习的应用

前言

      强化学习的目的是寻找最优策略。其中涉及两个核心概念最优状态值和最优策略，以及贝尔曼最优公式。而贝尔曼最优公式用不动点原理求解地址，由Banach不动点定理可以知道，强化学习一定存在唯一的解（策略）  ,并且可以通过迭代求得。

1.贝尔曼方程

      贝尔曼方程在强化学习（RL）中无处不在，由美国应用数学家理查德·贝尔曼（Richard Bellman）提出，用于求解马尔可夫决策过程。

       贝尔曼最优性方程是一个递归方程，在有模型环境由动态规划（DP）算法求解时，可以通过求解该方程可以找到最优值函数和最优策略。

先提出三个概念：

1.对于任何有限的MDP，都存在一个最佳策略π*，满足其他所有可能的策略π都不会比这个策略更好。

2.如果对于状态空间中的每个状态，使用π1派生的值函数在此状态的值都大于或等于使用π2派生的值函数在此状态的值，则可以说策略π1优于策略π2

3.采用巴拿赫不动点定理证明始终存在一个比所有其他策略都更好的策略，方法是证明贝尔曼最优算子是对带有L-无穷范数度量的实数完备度量空间上的闭映射。

2 巴纳赫不动点

2.1.距离空间

2.2.1 定义

简单理解：空间，就是在一个集合上定义某种规则（函数），且该规则适合集合内每一个元素。

        比如：对于海洋空间（集合），就是指“四大洋中所有的水分子（元素），在自然状态（规则）可以到达的任意位置的集合”。基于这个定义，四大洋合在一块是海洋空间，各自独立也是海洋空间，而水球内的空间不属于海洋空间，因为自然状态（规则）海洋的水无法进入。

距离空间：就是在一个集合上，定义两个点的距离函数（规则）对集合中任意两个点之间都成立。

2.2 延深理解

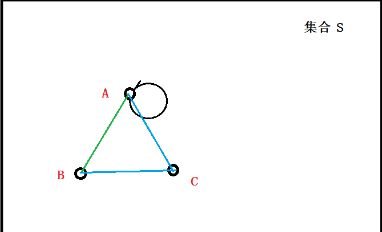
以下图为例，对上述定义公式进行文字化表述：

1.每个点和自己的距离为0，任两点间的距离为正数，

2.从A到B的距离，等同于从B到A的距离，

3.从A到B的距离小于等于从A先经过C再到B的距离。

带入1.1定义的公式，表述如下：

在集合S中，任意一个点，比如A点，A到A的距离为0；写成

在集合S中，任意两个点，比如A点B点（不重合），其距离大于0；写成

在集合S中，任意三个点，比如A点B点C点（不重合），其距离有：B到A的距离，一定小于B到C的距离加上C到A的距离，写成：

2.压缩映射

f:X→X 是集合X到自身的一个映射，不动点就是指满足 f ( x ) = x  的任意点 x ∈ X .

压缩映射： ( X , d )  是一个距离空间，对映射 f : X → X 如果存在常数k，使得 0 < k < 1 ,且对任何 x , y ∈ X 有 d ( f ( x ) , f ( y ) ) ≤ k d ( x , y ) ，则称f为压缩映射。

简单理解：就是在映射之后两点的距离变短了(0< k < 1)，就是压缩了
 

3.不动点原理

Banach 不动点定理如下：

解释：巴拿赫不动点定理通常被叫作压缩映射原理，它用构造性的方法证明了度量（距离）空间中某些特殊映射（压缩映射）不动点的存在性和唯一性。如果某个函数在某个点收敛，那么该函数在那个收敛点的值就是收敛点本身。因此，这个收敛点就是不动点

简单理解：我们可以想象有一张地图，然后将它按照不同的比例进行缩小，得到的每一张新图片和原图总是只有唯一的一个点重合！并且如果我们定义了一个压缩映射，则从图中任意一个点开始采用迭代法最后总能收敛到不动点。

数学应用：

1.非线性常微分方程解的存在性

2.非线性两点边值问题的(经典)解的存在性

3.巴纳赫不动点解决贝尔曼方程（强化学习）

3.1柯西序列（补充）

      对于距离空间（X，d），空间元素组成的序列（x1，x2，x3 … xn）如果在某个点收敛（它们无限接近于某个点），这个序列就是柯西序列。

3.2求解最优值

如何求解最优值？
对于一个完整的度量空间，将压缩映射一遍又一遍地应用到集合的元素上，我们最终将得到唯一的一个最优值。我们知道：

1. 压缩映射将集合中元素聚集到一起。

2. 不断运用压缩映射，得到一个柯西序列。

3. 完备度量空间中的柯西序列始终会收敛自身中的一个值。

3.3解决

 基于L-无穷范数度量：根据此度量空间范数的定义，两个值函数之间的距离等于两个值函数向量各方向绝对值之差的最大值。同样，对于有限奖励的有限MDP，值函数将始终在实数空间中。因此，此有限空间是完备的。此外贝尔曼算子B是压缩映射。

因此，根据巴拿赫不动点定理，我们得出结论：
对每个MDP，存在唯一的最优值函数V *，使用这个值函数，我们可以得到最优策略π *。

因此证明，对于任何有限的MDP，都存在一个最优策略π *，不差于其他所有可能的策略π。

策略迭代和值迭代的区别：
      1.策略迭代选择初始随机策略，通过策略评估-策略改进-反复迭代直至策略最优；
      2.价值迭代利用Banach不动点定理，迭代的方法求解Bellman最优方程，通过寻找最优价值函数，再提取最优策略，因为值函数一旦最优，那么策略也一定最优（保证收敛），策略迭代更快速高效一点。

      策略迭代和价值迭代都用到了动态规划方法和自益的思想。

不动点在强化学习中的应用参考：地址

不动点在GNN中的应用参考：地址

参考文献

1.【泛函分析】距离空间和赋范空间_距离空间和赋反空间-CSDN博客

2.机器学习系列5：距离空间（1）_距离空间中b(1,4)表示什么)-CSDN博客 

3.（I）Banach空间和不动点定理 （1） - 知乎 

4.泛函分析笔记(十) 不动点定理及其应用_f(x)到xf(x)的是什么映射-CSDN博客 

4.强化学习之动态规划_策略改进定理-CSDN博客 

5.巴拿赫不动点定理_证明不动点巴拿赫空间-CSDN博客 

6.参考书：强化学习：原理与Python实现 

7.强化学习：贝尔曼最优公式_~hello world~的博客-CSDN博客 

8.转载：强化学习中Bellman最优性方程背后的数学原理？_贝尔曼最优性原理_IEEEagent RL的博客-CSDN博客