递归玩转动态规划
汇总LeeCode前200题中所有涉及动态规划的算法题，用自己的逻辑整理此类问题的优化思路。
动态规划
-
- 概述
- 最长回文子串
- 字符串匹配问题
- 最长有效括号
- 编辑距离
- 交错字符串
- 最大子序和
- 不同路径问题
- 最小路径和
- 扰乱字符串
- 解码方法
- 不同的二叉搜索树
- 不同的子序列
概述
新手上路，详细记录了下刷LeeCode动态规划专题的相关题目，文笔有限，一方面分享，另一方面也总结给自己复习，如果错误的地方，欢迎大神批评指证。
那么正式开始，动态规划的题型，最主要的步骤就是如何快速的构造记忆dp数组，但是往往dp数组的建议并不是特别容易，需要我们理解所记录的状态的具体含义，会给接替带来较大的难度。
面对动态规划的题，我一般尝试用暴力递归的方式去进行尝试，然后在暴力递归的基础上用动态规划思想去优化，往往解题变得简单明了。
最长回文子串
LeeCode5. 最长回文子串
这题是leeCode非常经典的一道题，他的最优解法是Manacher算法，可以实现O(N)的平均时间复杂度。这里要呈现此题的动态规划解答，不对最优的解法详细阐述，后面仅提供一下Manacher的代码。
-
首先需要找出字符串中的最长回文子串，也就是返回字符串从0 - n (字符串长度)之间的最长回文子串,暴力递归尝试如下。
-
情况一： 如果当前字符串的头尾字符相等，那么有可能整体都是回文字符，进入下一层判别条件。子情况一： 头尾各缩进一位的子字符串如果是回文串，那么整体的s就是最长的回文子串。子情况二： 头尾各缩进一位的字符串如果不是回文串，那么整体的s肯定不是回文串，将此处的情况当成下面的情况考虑。
-
情况二： 如果当前的字符串头尾字符不相等 ，那么当前的字符串肯定不是回文字符。所以当前字符串的最大回文子串可能出自两个地方。左边缩进一个字符后的字符串的最大回文字符串或者右边缩进一个字符后的字符串的最大回文字符串。
-
好了，经过场面的三个步骤，暴力递归的思想就出来了，那么递归还要考虑结束条件。
-
结束条件：当缩进步骤发生后，如果成了只有一个字符的字符串，那么肯定是回文串，返回即可。
-
暴力版的暴力递归代码如下：
// 最长回文子串的暴力递归解法
public String longestPalindrome(String s) {
// 直接暴力一点返回结果
return getRes(s,0,s.length() - 1);
}
// 真正的技术在这里
private String getRes(String s, int l, int r) {
// 两个边界条件首先放上
if(l == r) return s.charAt(l) + "";
if(l > r) return "";
// 分析出来的情况一（如果两头都缩进后的最大回文子串长度不等于缩进后字符串，那么子字符串肯定也不是回文字符串）
if (s.charAt(l) == s.charAt(r) && getRes(s,l+1,r-1).length() == r - l - 1) {
return s.substring(l,r+1);
}else{
// 分析对应的情况er
String s1 = getRes(s,l+1,r);
String s2 = getRes(s,l,r-1);
String ans = s1;
// 返回较长的结果
ans = ans.length() < s2.length() ? s2 : ans;
return ans;
}
}
- 走到这里基本思想已经有了，但是这个代码在LeeCode上面AC了39个案列就报了超时。那么下面就是要进行优化了，这里也就正式表现出了动态规划的强大之处，也可以更直观的理解暴力递归的操作逻辑。
- 观察暴力递归的代码，我们可以发现当前的字符串的最大回文子串的求解，是在子问题的基础上分析得出来的，那么现在我们将子问题罗列出来：
- 求缩进字符串左右各一个字符后的字符串的最大回文子串（问题一样，只是求解的对象变了，这就是递归的本质）
- 求左边缩进一个字符后的字符串的最大回文子串。
- 求左边缩进一个字符后的字符串的最大回文子串。
- 在暴力递归中我们是不断的递归下去，从大问题深入到子问题，一路走到底，然后计算再一路回传，那么这其中就回带来大量的重复计算。举一个例子： 求解s[1 - 4]位置时可能会计算s[ 2 - 4 ]位置的最大回文字符串，然而当求解s[2 - 5]的字符串时，又有可能要重新计算了一遍s[2 - 4]位置的字符串。这个就是严重的重复计算。
- 有了上面例子的解释，那么动态规划的优化工作之一就可以看出来了，存储重复计算的结果，我们用户一张表记录下s[2 - 4]的结果就可以了，当然这里如果用HashMap存储中间结果也是可以的，时间复杂会也会降低，但是效率还是没有动态规划好。
- 回到题目，起始我们就可以看出几个简单的结果， 比如当
l == r , r > r的结果我门可以直观的看出来，那么我们动态规划的思想就是从这里出发去推导大的问题。 - 这里直接对着暴力递归的代码直接来进行动态规划，我们将暴力递归中的l指针，看作是二维数组的行数，r指针看作是数组的列数，那么一张边长为s长度的二维数组就创建出来了，存储的结果就是暴力递归中返回的结果，不难看出，如果要求某个格子的最大回文子串的时候，我们只需要他左边格子的信息，下面格子的信息，以及左下角格子的信息。那么下面的工作就是把这么一张二维数组中的每一个位置都填上元素就可以了。
- 很显然，在遍历数组填元素之前，有一半以上的格子我们可以明确的知道它的值，比如 当l > r时，此格子填空字符串，l == r 时，此位置填上单个字符串。然后根据暴力递归的判断条件填格子。
- 填格子的代码如下：
// 暴力递归改动态规划
public String longestPalindrome2(String s){
if(s.length() < 2) return s;
int n = s.length();
String[][] dp = new String[n][n];
for (int i = n - 1; i >= 0; i--) {
for (int j = 0; j < n; j++) {
if(i > j){
dp[i][j] = "";
}else if(i == j) {
dp[i][j] = s.charAt(i) + "";
}else if(s.charAt(i) == s.charAt(j) && dp[i+1][j-1].length() == j - i - 1){
dp[i][j] = s.substring(i,j+1);
}else{
// 找出三个之中最长的
String s1 = dp[i+1][j]; // 左边缩进一位的结果
String s2 = dp[i][j - 1]; // 右边缩进一位的结果
String cur = s1;
cur = cur.length() < s2.length() ? s2 : cur;
dp[i][j] = cur;
}
}
}
return dp[0][n - 1];
}
- 这里就是动态规划的雏形了，很可惜leeCode上运行还是超时，不过AC过了119个案例，大大提升了性能。好了，那么后面就是通用的二维表格优化了。分析一下时间都浪费在哪里，整体代码遍历二维数组肯定没问题，那么问题肯定出在了计算s1, s2的长度以及比较大小上面了。
- 考虑到这里遍历的每一个i,j都是元素的起始位置，那么我们可以不用直接将返回结果存档在数组中，我们直接用一个boolean数组记录，当前的位置是不是回文串就行了
- 在之前分析的情况一下； 如果头尾各缩进一个字符后的子字符串是回文串，那么当前字符也是回文串，一旦确定了一个字符串是回文串，那么就用i ，j 的索引去定下他的长度和起始位置，不断更新即可。
- 在之前分析的情况二下，该位置不是回文串，那么没有利用价值，直接false即可，避免了之前的比较字符串长度的操作。
- 优化后的代码如下：
// 优化动态规划(继续优化)
public String longestPalindrome4(String s){
if(s.length() < 2) return s;
int n = s.length();
boolean[] dp = new boolean[n];
int maxLen = 0;
int maxS= 0;
int maxE = 0;
for (int i = n - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
if(i > j){
dp[j] = true;
}else if(i == j) {
dp[j] = true;
}else if(s.charAt(i) == s.charAt(j) && dp[j-1]){
dp[j] = true;
if(maxLen < (j - i)){
maxLen = j - i;
maxS = i;
maxE = j;
}
}else{
dp[j] = false;
}
// 其他情况下全部置为false
}
}
return maxLen == 0 ? s.substring(0,1) : s.substring(maxS,maxE + 1);
}
- 同样这段代码也AC过了，时间成本上没什么改变，空间降了4M的内存，还是有非常明显的提升。
- 补充： 不知不觉写了这么多，以上展示的最优版本的代码虽然AC了，但是运行时间复杂还是比较高，这是我能用DP方法做的最好的效果了，欢迎大神批评指证，下面就附上这道题的最优解法Manacher算法，不过多解释，以后在写一个Manacher笔记好好理解一下，这里也给自己打个样。
public String longestPalindrome4(String s) {
if(s.equals("")) return s;
String ret = tackleString(s);
int n = ret.length();
int[] bj = new int[n]; // 存放每个位置的回文半径
int maxR = -1; // 存放当前的最大回文右边界
int cC = -1; // 存放当前最大回文右边界对应的回文中心
// 遍历s字符串
for (int i = 0; i < n; i++) {
// 如果当前位置在最大回文右边界内，则在当前位置与右边界之间的距离和前半部分的回文半径中去最小值
// 如果在边界或者maxR外边，默认半径为1，然后进行中心扩展
bj[i] = maxR > i ? Math.min(maxR - i,bj[(2 * cC) - i]) : 1;
// 中心扩展
while(i - bj[i] >= 0 && i + bj[i] < n){
if(ret.charAt(i - bj[i]) == ret.charAt(i + bj[i])){
bj[i]++;
}else{
break;
}
}
// 扩展结束之后，更新maxR和cC
if(i + bj[i] > maxR){
maxR = i + bj[i];
cC = i;
}
}
// 找出当前半径数组中的最大半径
int maxLen = bj[0];
int center = 0;
for (int i = 1; i < bj.length; i++) {
if(bj[i] > maxLen){
maxLen = bj[i];
center = i;
}
}
// 有了最大的回文半径和最大的回文中心，返回字符串即可
int start = (center - maxLen + 1) / 2;
int end = (center + maxLen) / 2;
return s.substring(start,end);
}
// 改造字符串————给字符串加上虚轴
private String tackleString(String s) {
int n = s.length();
String ret = "#";
for (int i = 0; i < n; i++) {
ret += s.charAt(i) + "#";
}
return ret;
}
字符串匹配问题
两道经典的leeCode题，都是hard级别的。
LeeCode10. 正则表达式匹配
好的，接下来继续撸第二道经典题，字符串匹配问题，问题如下：
问题一： 正则表达式匹配
给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
’ . ’ 匹配任意单个字符
’ * ’ 匹配零个或多个前面的那一个元素
思路分析：
- 首先还是建立暴力递归的思想：如果我们要求整体字符串s和p是否可以匹配，可以通过s和p的前缀字符串的匹配信息来推导出当前字符串的匹配情况。这里给一张图展示思路过程，绿色小旗子我们可以直接返回的结果，不需要计算，红色小旗子依赖子问题的求解。
- 下面就是将思路用代码实现： 用两个指针cs,cp分别表示当前需要匹配s的前cs个字符串和p的前cp个字符串。
// LeeCode10: 正则表达式匹配
public boolean isMatch(String s, String p) {
return getMatchRes(s, s.length(), p, p.length());
}
// cs当前选定s字符串取得前cs各字符串，cp指针表示选定当前p字符串的前cp个字符
private boolean getMatchRes(String s, int cs, String p, int cp) {
// 边界条件，如果p的指针cp走到头了，s的指针没走到头，肯定匹配不上返回false
if (cp == 0) return cs == 0;
if (cp < 0) return false;
// 如果s为null，
if (cs == 0) {
if (p.charAt(cp - 1) == '*') {
return getMatchRes(s, cs, p, cp - 2);
} else {
return false;
}
}
// 分情况讨论：
// 情况一：如果当前的cs和cp位置的字符相等，或者cp位置的字符是'.',那么直接返回s和p格子前进一位的结果
if (s.charAt(cs - 1) == p.charAt(cp - 1) || p.charAt(cp - 1) == '.') {
return getMatchRes(s, cs - 1, p, cp - 1);
}
// 情况二，当前s和p位置的字符不相等时，两种可能性，一个时p为'*',还有一个p为字母
if (p.charAt(cp - 1) == '*') {
if ((cp < 2 || (s.charAt(cs - 1) != p.charAt(cp - 2)) && p.charAt(cp - 2) != '.')) {
return getMatchRes(s, cs, p, cp - 2);
} else {
return getMatchRes(s, cs - 1, p, cp) || getMatchRes(s, cs, p, cp - 1) || getMatchRes(s, cs, p, cp - 2);
}
}
return false;
}
这把就很爽了，一次AC，不过必须要优化的，暴力递归的重复计算是不能接收的。继续分析递归代码：
- 创建一个
boolean[][]类型的dp数组，数组中存放的元素就是暴力递归每个步骤的结果，那么dp的属性很容易就可以定出来，dp = new boolean[s.length()][p.length(0)] - 从递归代码可以看出当前的格子依赖上面的格子，左一位的格子，以及左二位的格子，直接将格子替换到代码里面，如下：
class Solution {
// LeeCode10: 正则表达式匹配
public boolean isMatch(String s, String p) {
if(p.equals("")) return s.equals("");
// 创建dp数组
boolean[][] dp = new boolean[s.length() + 1][p.length() + 1];
// 遍历数组填数组
for (int i = 0; i <= s.length(); i++) {
for (int j = 0; j <= p.length(); j++) {
if(i == 0 && j == 0){
dp[i][j] = true;
}else if(j == 0){
dp[i][j] = false;
}else if(i == 0){
if(p.charAt(j - 1) == '*' && j - 1 > 0){
dp[i][j] = dp[i][j - 2];
}else{
dp[i][j] = false;
}
}else if(s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.') {
dp[i][j] = dp[i - 1][j - 1];
}else if(p.charAt(j - 1) == '*'){
if (j > 1 && (s.charAt(i - 1) != p.charAt(j - 2)) && p.charAt(j - 2) != '.') {
dp[i][j] = dp[i][j - 2];
} else if(j == 1){
dp[i][j] = false;
} else{
dp[i][j] = dp[i - 1][j] || dp[i][j - 1] || dp[i][j - 2];
}
}else{
dp[i][j] = false;
}
}
}
return dp[s.length()][p.length()];
}
}
- 顺利AC，继续优化，boolean类型默认值为false，所有有很多没有必要写上去代码，优化结果如下：
class Solution {
// LeeCode10: 正则表达式匹配
public boolean isMatch(String s, String p) {
if(p.equals("")) return s.equals("");
// 创建dp数组
boolean[][] dp = new boolean[s.length() + 1][p.length() + 1];
// 遍历数组填数组
for (int i = 0; i <= s.length(); i++) {
for (int j = 0; j <= p.length(); j++) {
if(i == 0 && j == 0){
dp[i][j] = true;
}else if(j == 0 || (j == 1 && p.charAt(j - 1) == '*')){
dp[i][j] = false;
}else if(i == 0){
if(p.charAt(j - 1) == '*' && j - 1 > 0){
dp[i][j] = dp[i][j - 2];
}
}else if(s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.') {
dp[i][j] = dp[i - 1][j - 1];
}else if(p.charAt(j - 1) == '*'){
if ((s.charAt(i - 1) != p.charAt(j - 2)) && p.charAt(j - 2) != '.') {
dp[i][j] = dp[i][j - 2];
} else{
dp[i][j] = dp[i - 1][j] || dp[i][j - 1] || dp[i][j - 2];
}
}
}
}
return dp[s.length()][p.length()];
}
}
- 走到这里，这个问题的执行效率已经非常高了，当然这里空间上还可以继续优化，不过对于列而言，需要依赖左边两个格子的状态，所以感觉有一定难度，这里不花时间去琢磨了，有机会再回头来试试。
下面再上一题如出一辙的题目，只是稍微变动了一点点。
LeeCode44. 通配符匹配
思路分析： 这题起始和上一题是一样的，只是’*'可以匹配的范围变简单了一点。下图是暴力递归的分析思路。
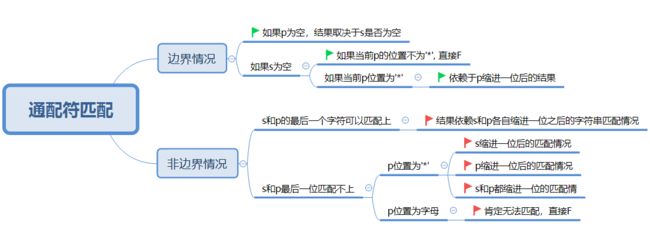
暴力递归代码如下：
class Solution {
public boolean isMatch(String s, String p) {
return getRes(s,s.length(),p,p.length());
}
private boolean getRes(String s, int cs, String p, int cp) {
if(cp == 0) return cs == 0;
if(cs == 0) {
return p.charAt(cp - 1) == '*' && getRes(s,cs,p,cp - 1);
}
if(s.charAt(cs - 1) == p.charAt(cp - 1) || p.charAt(cp - 1) == '?'){
return getRes(s,cs - 1,p,cp - 1);
}
if(p.charAt(cp - 1) == '*'){
return getRes(s,cs - 1,p,cp) || getRes(s,cs,p,cp - 1) || getRes(s,cs - 1,p,cp- 1);
}
return false;
}
}：
使用二维数组进行优化，代码如下：
// 动态规划优化
public boolean isMatch(String s, String p) {
if(p.equals("")) return s.equals("");
boolean[][] dp = new boolean[s.length() + 1][p.length() + 1];
for (int i = 0; i <= s.length(); i++) {
for (int j = 0; j <= p.length(); j++) {
if(i == 0 && j == 0) {
dp[i][j] = true;
}else if(j == 0) {
dp[i][j] = false;
}else if(i == 0) {
dp[i][j] = p.charAt(j - 1) == '*' && dp[i][j - 1];
}else if(s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '?'){
dp[i][j] = dp[i - 1][j - 1];
}else if(p.charAt(j - 1) == '*'){
dp[i][j] = dp[i - 1][j] || dp[i][j - 1] || dp[i - 1][j - 1];
}
}
}
return dp[s.length()][p.length()];
}
最长有效括号
32. 最长有效括号
思路分析:
- 这道题的关键就在于理解扩号字符串组成规律，摸清楚规律之后，编码就不是很么难事。
- 有效括号字符串有几个性质： 左括号的数量必须等于右括号的数量，字符串必须以
(开头,以)结尾。 - 下面给出分析思路：
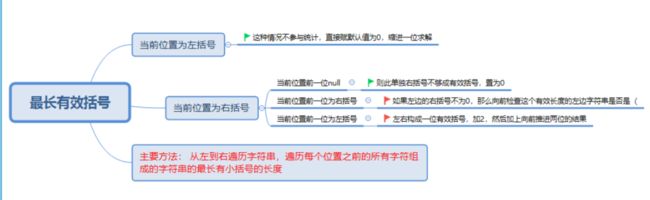
- 根据分析的思路，上暴力递归代码：
public int longestValidParentheses2(String s) {
getRes(s,s.length() - 1);
return maxLen;
}
int maxLen = 0; // 放一个指针，用于记录最长的结果
// c为字符串的索引，用于记录每个位置的最长有效括号的长度，只对右括号有效
private int getRes(String s, int c) {
// 扣边界
if(c <= 0) return 0;
if(s.charAt(c) == '('){ // 如果当前位置是'('，则缩进一位去考虑，此处直接返回0
getRes(s,c - 1);
return 0;
}
// 到这里c位置只可能是')'
int ans = 0;
if(s.charAt(c - 1) == '(') {
ans = 2 + getRes(s,c - 2); // 向前走两位
} else { // 如果左边同样为右括号
int left = getRes(s,c - 1); // 用一个指针，记录他的值
if(left != 0 && c - left - 1 >= 0 && s.charAt(c - left - 1 ) == '(') {
ans = 2 + left + getRes(s,c-left-2);
}
}
maxLen = Math.max(ans,maxLen); // 每次走到这里都更新maxLen的值
return ans;
}
- 同样的，老套路，暴力递归改成动态规划。
// 暴力递归改动态规划
public int longestValidParentheses2(String s) {
int maxLen = 0;
int[] dp = new int[s.length()];
for (int i = 0; i < s.length(); i++) {
if(i == 0 || s.charAt(i) == '('){
dp[i] = 0;
}else{
if(s.charAt(i - 1) == '('){
dp[i] = 2 + (i - 1 > 0 ? dp[i - 2] : 0);
}else{
if(dp[i - 1] != 0 && i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '('){
dp[i] = 2 + dp[i - 1] + (i - dp[i - 1] - 1 > 0 ? dp[i - dp[i - 1] - 2] : 0);
}
// 其他情况默认为0
}
}
maxLen = Math.max(maxLen,dp[i]);
}
return maxLen;
}
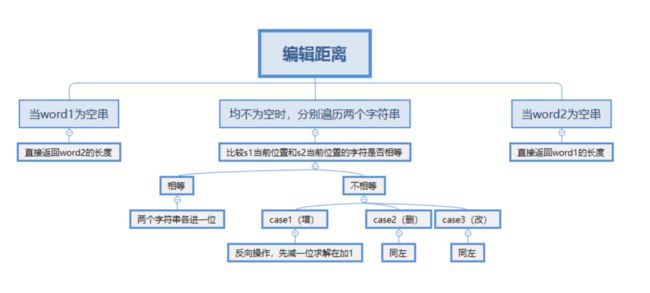
编辑距离
再上一道难题，优势字符串问题，总结了一下规律，字符串问题大部分都可以用动态规划去求解。
LeeCode72. 编辑距离
- 首先理解一下暴力递归的思路：
- 下面展示出暴力递归的代码，这里用了哈希表存储了中间重复计算的结果，在很多情况下这是一个非常好用的方法，但是他的效果和动态规划还是有非常大的差距。
// 编辑距离
public int minDistance2(String word1, String word2) {
if(word1.equals("")) return word2.length();
if(word2.equals("")) return word1.length();
HashMap<String,Integer> memo = new HashMap<>();
return getRes(word1,0,word2,0,memo);
}
// 暴力递归，添加一个哈希map存储重复计算的结果
private int getRes (String s1, int c1, String s2, int c2,HashMap<String,Integer> memo) {
if(c1 == s1.length()) return s2.length() - c2;
if(c2 == s2.length()) return s1.length() - c1;
String key = c1 + "@" + c2;
if(memo.containsKey(key)) return memo.get(key);
int ans = 0;
if(s1.charAt(c1) == s2.charAt(c2)){
ans = getRes(s1,c1 + 1, s2, c2 + 1,memo);
}else{
int add = getRes(s1,c1 + 1, s2, c2,memo);
int del = getRes(s1,c1,s2,c2 + 1,memo);
int modify = getRes(s1,c1+1,s2,c2 + 1,memo);
ans = 1 + Math.min(add,Math.min(del,modify));
}
memo.put(key,ans);
return ans;
}
- 下面再用dp数组优化一下代码，构成动态规划。
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = len1; i >= 0; i--) {
for (int j = len2; j >= 0; j--) {
if(i == len1) {
dp[i][j] = len2 - j;
}else if(j == len2){
dp[i][j] = len1 - i;
}else if(word1.charAt(i) == word2.charAt(j)){
dp[i][j] =dp[i + 1][j + 1];
}else{
int add = dp[i + 1][j];
int del = dp[i][j + 1];
int modify = dp[i + 1][j + 1];
dp[i][j] = 1 + Math.min(add,Math.min(del,modify));
}
}
}
return dp[0][0];
}
}
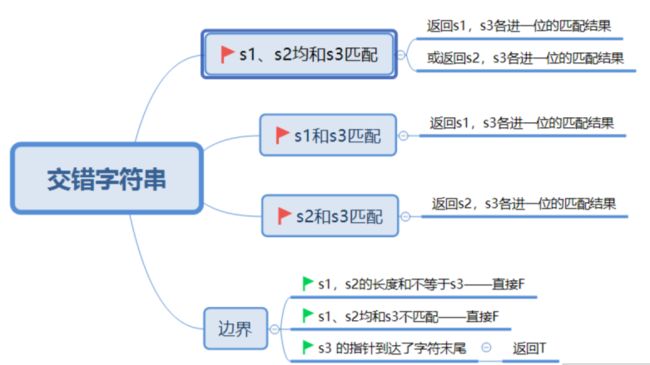
交错字符串
97. 交错字符串
继续上一道字符串的hard题。
- 首先理一下暴力递归的思路：
- 直接上暴力递归的代码
// 交错字符串
public boolean isInterleave(String s1, String s2, String s3) {
if(s1.length() + s2.length() != s3.length()) return false;
HashMap<String,Boolean> memo = new HashMap<>();
return getRes(s1,0,s2,0,s3,0,memo);
}
private boolean getRes(String s1, int c1, String s2, int c2, String s3, int c3, HashMap<String, Boolean> memo) {
if(c3 == s3.length()) return true;
if(c1 == s1.length()) return s2.substring(c2,s2.length()).equals(s3.substring(c3,s3.length()));
if(c2 == s2.length()) return s1.substring(c1,s1.length()).equals(s3.substring(c3,s3.length()));
String key = c1 + "@" + c2;
if(memo.containsKey(key)) return memo.get(key);
if(s1.charAt(c1) == s3.charAt(c3)) {
if(getRes(s1,c1+1,s2,c2,s3,c3+1,memo)){
memo.put(key,true);
return true;
}
}
if(s2.charAt(c2) == s3.charAt(c3)) {
if(getRes(s1,c1,s2,c2+1,s3,c3+1,memo)){
memo.put(key,true);
return true;
}
}
memo.put(key,false);
return false;
}
- 同样，动态规划优化如下
// 交错字符串
public boolean isInterleave(String s1, String s2, String s3) {
if(s1.length() + s2.length() != s3.length()) return false;
HashMap<String,Boolean> memo = new HashMap<>();
return getRes(s1,0,s2,0,s3,0,memo);
}
private boolean getRes(String s1, int c1, String s2, int c2, String s3, int c3, HashMap<String, Boolean> memo) {
if(c3 == s3.length()) return true;
if(c1 == s1.length()) return s2.substring(c2,s2.length()).equals(s3.substring(c3,s3.length()));
if(c2 == s2.length()) return s1.substring(c1,s1.length()).equals(s3.substring(c3,s3.length()));
String key = c1 + "@" + c2;
if(memo.containsKey(key)) return memo.get(key);
if(s1.charAt(c1) == s3.charAt(c3)) {
if(getRes(s1,c1+1,s2,c2,s3,c3+1,memo)){
memo.put(key,true);
return true;
}
}
if(s2.charAt(c2) == s3.charAt(c3)) {
if(getRes(s1,c1,s2,c2+1,s3,c3+1,memo)){
memo.put(key,true);
return true;
}
}
memo.put(key,false);
return false;
}
最大子序和
53. 最大子序和
- 这题的关键在于思想，构建合理的递推过程。
- 数组中的最大子序和一定是连续的，且一定以某个位置的元素结尾，那么求出以每个位置结尾的最大元素和，然后找出所有位置中的最大值。直接用数组保存，也是一种动态规划的思想。
class Solution {
public int maxSubArray(int[] nums) {
int[] dp = new int[nums.length];
dp[0] = nums[0];
int ans = nums[0];
for (int i = 1; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
ans = Math.max(ans, dp[i]);
}
return ans;
}
}
- 此题中当前格子只用到了前一个格子的信息，所以可以将dp数组直接用变量代替
public int maxSubArray2(int[] nums) {
int dp = nums[0];
int ans = nums[0];
for (int i = 1; i < nums.length; i++) {
dp = Math.max(dp + nums[i], nums[i]);
ans = Math.max(ans, dp);
}
return ans;
}
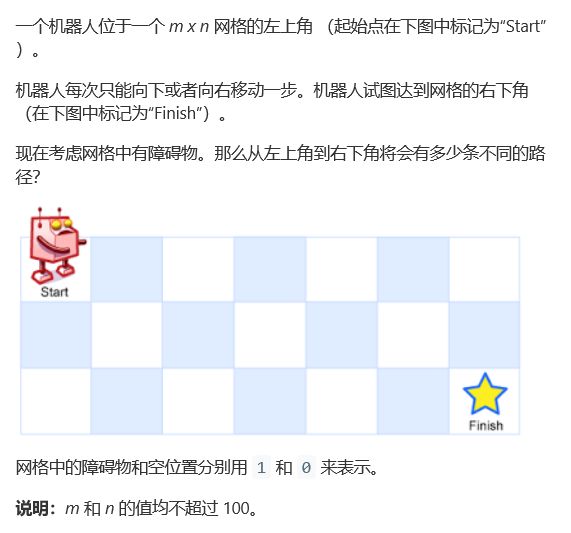
不同路径问题
62. 不同路径
这道题也是非常经典的一道题，经常用作动态规划的开山之作。
62. 不同路径
这道题也是非常经典的一道题，经常用作动态规划的开山之作。
这题非常明确的提供了一张二维数组，非常容易联想到动态规划，那么关键就是理解它的递推逻辑。
- 问题非常简单，小人只可以向下或者向右走，那么分别计算出向下和向右的路径和就可以求出最终的路径总数。
- 下图提供分析思路：
- 根据上图，构建暴力递归代码：
public static int uniquePaths(int m, int n) {
return getRes(0, 0, m, n); // 从0，0位置出发
}
private static int getRes(int r, int c, int m, int n) {
if (r == m - 1 || c == n - 1) return 1;
return getRes(r + 1, c, m, n) + getRes(r, c + 1, m, n); // 下边和加上右边和
}
- 感受一下暴力递归的华丽之处，代码非常简短，可惜超时
- 非常明确的知道，当前的格子依赖它右边和下面的格子，构建动态规划。
public static int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
if (i == m - 1 || j == n - 1) {
dp[i][j] = 1;
} else {
dp[i][j] = dp[i + 1][j] + dp[i][j + 1];
}
}
}
return dp[0][0];
}
- 完全依赖递归的思路修改，这里因为我们没求一个结果的时候，都只用到了下面的格子和右边的格子，所以完全可以降低dp数组的维度，只用一个一维数组不断更新就可以实现了。
public static int uniquePaths(int m, int n) {
int[] dp = new int[n];
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
if (i == m - 1 || j == n - 1) {
dp[j] = 1;
} else {
dp[j] = dp[j] + dp[j + 1];
}
}
}
return dp[0];
}
- 直接将dp的中有关i的位置全部干掉就可以了。
接下来是这题的延伸：
63. 不同路径 II
- 在64题的基础上加了障碍物，所以要稍微改动一下递归的思路。
- 改一下暴力递归的代码（超时）
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
return getRes(obstacleGrid,0,0,m,n);
}
private int getRes(int[][] obstacleGrid, int r, int c, int m, int n) {
if(obstacleGrid[r][c] == 1) return 0;
if(r == m - 1 && c == n - 1) return 1;
if(r == m - 1) return getRes(obstacleGrid,r,c + 1,m,n); // 向右走
if(c == n - 1) return getRes(obstacleGrid,r + 1,c,m,n); // 向下走
return getRes(obstacleGrid, r + 1, c, m, n) + getRes(obstacleGrid, r, c + 1, m, n);
}
}
- 补充一个哈希map提升性能的代码(可以AC)
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
HashMap<String, Integer> memo = new HashMap<>();
return getRes(obstacleGrid, 0, 0, m, n, memo);
}
private int getRes(int[][] obstacleGrid, int r, int c, int m, int n, HashMap<String, Integer> memo) {
if (obstacleGrid[r][c] == 1) return 0;
if (r == m - 1 && c == n - 1) return 1;
String key = r + "@" + c;
if (memo.containsKey(key)) return memo.get(key);
if (r == m - 1) {
int right = getRes(obstacleGrid, r, c + 1, m, n, memo);
memo.put(key, right);
return right; // 向右走
}
if (c == n - 1) {
int down = getRes(obstacleGrid, r + 1, c, m, n, memo);
memo.put(key, down);
return down; // 向下走
}
int ans = getRes(obstacleGrid, r + 1, c, m, n, memo) + getRes(obstacleGrid, r, c + 1, m, n, memo);
memo.put(key, ans);
return ans;
}
}
- 递归改动态规划，直接按照递归的逻辑来
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
if (obstacleGrid[i][j] == 1) {
dp[i][j] = 0;
continue;
}
if (i == m - 1 && j == n - 1) {
dp[i][j] = 1;
} else if (i == m - 1) {
dp[i][j] = dp[i][j + 1];
} else if (j == n - 1) {
dp[i][j] = dp[i + 1][j];
} else {
dp[i][j] = dp[i + 1][j] + dp[i][j + 1];
}
}
}
return dp[0][0];
}
}
- 空间上一样可以优化
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[] dp = new int[n];
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
if (obstacleGrid[i][j] == 1) {
dp[j] = 0;
continue;
}
if (i == m - 1 && j == n - 1) {
dp[j] = 1;
} else if (i == m - 1) {
dp[j] = dp[j + 1];
} else if (j == n - 1) {
dp[j] = dp[j];
} else {
dp[j] = dp[j] + dp[j + 1];
}
}
}
return dp[0];
}
}
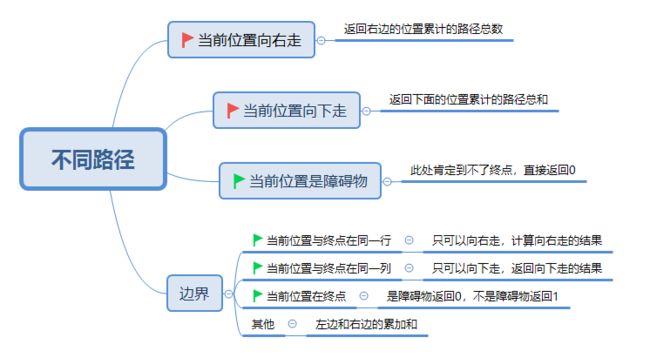
最小路径和
64. 最小路径和
继续来一道类似的题目：
- 递归思路如下：
- 递归代码实现
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
return getRes(grid,0,0,m,n);
}
private int getRes(int[][] grid, int r, int c, int m, int n) {
if(r == m - 1 && c == n - 1) return grid[m - 1][n - 1];
if(r == m - 1) return grid[r][c] + getRes(grid, r, c + 1, m, n);
if(c == n - 1) return grid[r][c] + getRes(grid, r + 1, c, m, n);
return grid[r][c] + Math.min(getRes(grid, r + 1, c, m, n),getRes(grid, r, c + 1, m, n));
}
}
- memo优化
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
HashMap<String,Integer> memo = new HashMap<>();
return getRes(grid,0,0,m,n,memo);
}
private int getRes(int[][] grid, int r, int c, int m, int n, HashMap<String,Integer> memo) {
if(r == m - 1 && c == n - 1) return grid[m - 1][n - 1];
String key = r + "@" + c;
if(memo.containsKey(key)) return memo.get(key);
if(r == m - 1) {
int right = grid[r][c] + getRes(grid, r, c + 1, m, n, memo);
memo.put(key,right);
return right;
}
if(c == n - 1) {
int down = grid[r][c] + getRes(grid, r + 1, c, m, n, memo);
memo.put(key,down);
return down;
}
int ans = grid[r][c] + Math.min(getRes(grid, r + 1, c, m, n, memo), getRes(grid, r, c + 1, m, n, memo));
memo.put(key,ans);
return ans;
}
}
- 动态规划
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int[][] dp = new int[m][n];
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
if (i == m - 1 && j == n - 1) {
dp[i][j] = grid[i][j];
} else if (i == m - 1) {
dp[i][j] = grid[i][j] + dp[i][j + 1];
} else if (j == n - 1) {
dp[i][j] = grid[i][j] + dp[i + 1][j];
} else {
dp[i][j] = grid[i][j] + Math.min(dp[i + 1][j], dp[i][j + 1]);
}
}
}
return dp[0][0];
}
}
- dp数组降维
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int[] dp = new int[n];
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
if (i == m - 1 && j == n - 1) {
dp[j] = grid[i][j];
} else if (i == m - 1) {
dp[j] = grid[i][j] + dp[j + 1];
} else if (j == n - 1) {
dp[j] = grid[i][j] + dp[j];
} else {
dp[j] = grid[i][j] + Math.min(dp[j], dp[j + 1]);
}
}
}
return dp[0];
}
}
扰乱字符串
87. 扰乱字符串
判断给定的两个字符串是不是扰乱字符串：
- 思路分析：
- 找到边界条件：s1和s2不等长或者s1和s2的组成字符不相同，直接返回false
- 找递归思路：将s1一份为二，形成多种不同的可能性，然后按个去和s2比较尝试，如果匹配上了，返回false；
- 暴力递归代码如下：
// memo技术优化
public boolean isScramble(String s1, String s2){
return process(s1,s2,new HashMap<String, Boolean>());
}
private boolean process(String s1, String s2, HashMap<String,Boolean> memo){
String key = s1 + "@" + s2;
if(memo.containsKey(key)){
return memo.get(key);
}
// 首先如果两个字符串长度不一样一定为false’
if(s1.equals(s2)) {
memo.put(key,true);
return true;
}
if(s1.length() != s2.length()){
memo.put(key,false);
return false;
}
int[] flag = new int[26];
for (int i = 0; i < s1.length(); i++) {
flag[s1.charAt(i) - 'a']++;
flag[s2.charAt(i) - 'a']--;
}
for (int i = 0; i < flag.length; i++) {
if(flag[i] != 0){
memo.put(key,false);
return false; // 存在啊u不一样的字母
}
}
// 进入暴力递归
for (int i = 1; i < s1.length(); i++) {
if(process(s1.substring(0,i),s2.substring(0,i),memo) && process(s1.substring(i),s2.substring(i),memo)){
memo.put(key,true);
return true;
}
if(process(s1.substring(0,i),s2.substring(s1.length() - i),memo)
&& process(s1.substring(i),s2.substring(0,s2.length() - i),memo)){
memo.put(key,true);
return true;
}
}
memo.put(key,false);
return false;
}
- 动态规划优化：dp[i][j][k] : 表示以s1的j位置起始和s2的k位置起始的长度为i的字符串是否可以匹配
// 扰乱字符串
public boolean isScramble(String s1, String s2) {
if (s1.equals(s2)) return true;
int[] temp = new int[26];
// 检查两个字符串构成字符集是否一样
for (int i = 0; i < s1.length(); i++) {
temp[s1.charAt(i) - 'a']++;
temp[s2.charAt(i) - 'a']--;
}
for (int i = 0; i < 26; i++) {
if (temp[i] != 0) return false;
}
int len = s1.length();
// 创建辅助数组，dp[i][j][k] 表示长度为i时，s1从j 到 j+i的字符串是否可以和s2k 到 k + i 的字符串匹配
// 返回结果为 dp[len][0][0];
boolean[][][] dp = new boolean[len + 1][len][len];
for (int i = 1; i <= len; i++) {
for (int j = 0; j + i <= len; j++) {
for (int k = 0; k + i <= len; k++) {
if (i == 1) {
dp[i][j][k] = s1.charAt(j) == s2.charAt(k);
} else {
for (int l = 1; l <= i; l++) {
dp[i][j][k] = (dp[l][j][k] && dp[i - l][j + l][k + l]) || (dp[l][j][k + i - l] && dp[i - l][j + l][k]);
if (dp[i][j][k]) { // 如果找到了true,直接跳出来
break;
}
}
}
}
}
}
return dp[len][0][0];
}
解码方法
思路分析：
- 字符串解码问题，同样用一个指针c来遍历字符串，计算每次遍历的结果累加，思路如下：
- 暴力递归首先分析思路：
public int numDecodings(String s) {
int len = s.length();
return getRes(s, 0, len);
}
private int getRes(String s, int c, int len) {
// 结束条件
if (c == len) return 1;
if (s.charAt(c) == '0') return 0;
if (c == len - 1) return 1;
// 首先将当前的单个元素解码，计算后面的解码总数
int n1 = getRes(s, c + 1, len);
// 然后检查当前元素后面的元素和当前的元素组合是否可以构成有效字符
int cur = (s.charAt(c) - '0') * 10 + (s.charAt(c + 1) - '0');
return cur <= 26 ? n1 + getRes(s, c + 2, len) : n1;
}
- 动态规划优化(完全一样的思路，直接修改代码非常简单)
public int numDecodings(String s) {
int len = s.length();
int[] dp = new int[len + 1];
dp[len] = 1;
for (int i = len - 1; i >= 0; i--) {
if (s.charAt(i) == '0') {
dp[i] = 0;
} else if (i == len - 1) {
dp[i] = 1;
} else {
int cur = (s.charAt(i) - '0') * 10 + (s.charAt(i + 1) - '0');
dp[i] = cur <= 26 ? dp[i + 1] + dp[i + 2] : dp[i + 1];
}
}
return dp[0];
}
不同的二叉搜索树
- 此题用递归的思想求解，弄清楚递归的逻辑，就会变得特别简单。
- 直接上递归代码
public List<TreeNode> generateTrees(int n) {
if(n < 1) return new ArrayList<>();
return getRes(1, n);
}
private List<TreeNode> getRes(int l, int r) {
List<TreeNode> ans = new ArrayList<>();
if (l == r) {
ans.add(new TreeNode(l));
return ans;
}
if (l > r) {
ans.add(null);
return ans;
}
for (int i = l; i <= r; i++) {
List<TreeNode> left = getRes(l, i - 1); // 返回左边的结果
List<TreeNode> right = getRes(i + 1, r); // 返回右边的结果
for (TreeNode t1 : right) {
for (TreeNode t2 : left) {
TreeNode root = new TreeNode(i);
root.left = t2;
root.right = t1;
ans.add(root);
}
}
}
return ans;
}
此题的另一种问法：
- 此题的逻辑跟上一题是一样的，所以直接在上面的递归代码上修改即可
public int numTrees(int n) {
if(n < 1) return 0;
return getRes(1, n);
}
private int getRes(int l, int r) {
if (l == r) {
return 1;
}
if (l > r) {
return 1;
}
int ans = 0;
for (int i = l; i <= r; i++) {
int left = getRes(l, i - 1); // 返回左边的结果
int right = getRes(i + 1, r); // 返回右边的结果
ans += left * right;
}
return ans;
}
- 看到getRes中的一大堆指针变量，直接改为动态规划
public int numTrees(int n) {
if(n < 1) return 0;
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
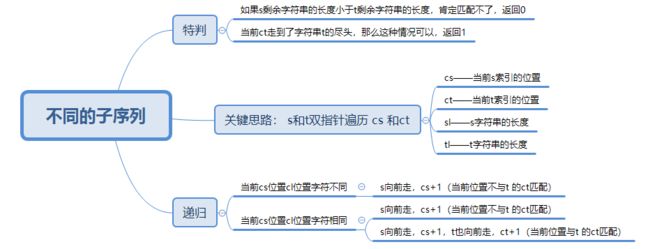
不同的子序列
115. 不同的子序列
- 思路分析： 传统的字符串匹配问题，考虑到每个元素的位置，当前元素可选可不选，分两条路走，构建出递归思想。
public int numDistinct(String s, String t) {
return getRes(s, t, 0, 0, s.length(), t.length());
}
private int getRes(String s, String t, int cs, int ct, int sl, int tl) {
if (sl - cs < tl - ct) return 0; // 长度不匹配直接返回0
if (ct == tl) return 1;
if (s.charAt(cs) != t.charAt(ct)) {
// 当前位置的s和t匹配不上，那么cs肯定不选，+1
return getRes(s, t, cs + 1, ct, sl, tl);
} else {
// 如果当前位置匹配上了， 那么两种情况的累加和，选和不选
return getRes(s, t, cs + 1, ct, sl, tl) + getRes(s, t, cs + 1, ct + 1, sl, tl);
}
}
- 将每一个子问题用动态规划的格子去表示，改成动态规划如下：这个dp不太好理解，但是结合动态规划修改就变得特别简单了
public int numDistinct(String s, String t) {
int lens = s.length();
int lent = t.length();
if(lens < lent) return 0;
int[][] dp = new int[lens + 1][lent + 1];
for (int i = lens; i >= 0; i--) {
for (int j = lent; j >= 0; j--) {
if(lens - i < lent - j){
dp[i][j] = 0;
}else if(j == lent){
dp[i][j] = 1;
}else{
if(s.charAt(i) != t.charAt(j)){
dp[i][j] = dp[i + 1][j];
}else{
dp[i][j] = dp[i + 1][j] + dp[i + 1][j + 1];
}
}
}
}
return dp[0][0];
}