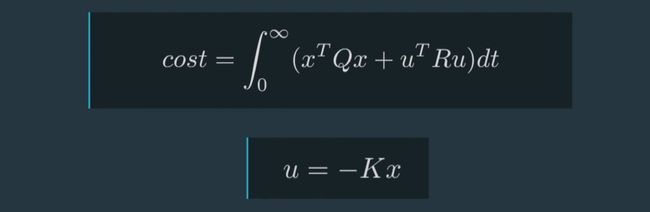Apollo课程学习6——控制
Apollo课程学习6——控制
- 学习前言
- 控制概述
-
- 一、控制的输入输出
- 二、控制模块
- 三、控制的作用
- 四、控制的性能要求
- 基于模型的控制方法
-
- 一、建模
- 二、系统辨识
- 三、控制器设计
-
- 1、滤波器设计
- 2、控制器设计
- 四、参数调优
-
- 1、PID控制
- 2、线性二次调节器(LQR)
- 3、模型控制预测(MPC)
- 4、自适应控制
- 5、鲁棒性控制(Robust Control)
- 6、离散化
- 工程应用
学习前言
控制概述
一、控制的输入输出
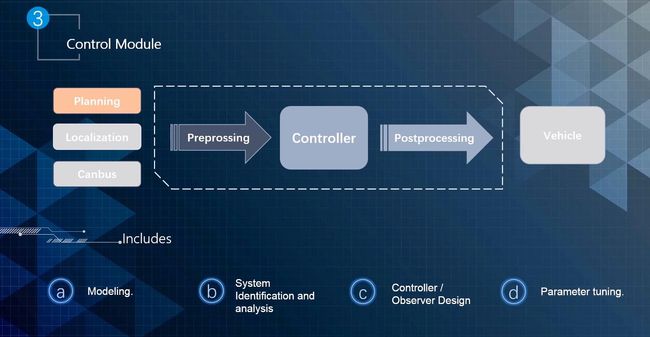
下图是Apollo自动驾驶框架的基本结构:

从图中可以看出,控制模块的输入一方面来自planning(规划模块),另一方面来自反馈阶段信息(如localization和HD Map),此部分信息包括车辆位置、朝向、速度等。
其输出结果是控制指令,与下层模块canbus(车辆交互标准)进行交互;同时控制模块也会从底层车辆得到反馈信号(车辆本身in vehicle reference frame:速度信息、四轮转速信息、车辆健康状况信息、底盘是否报错信息、危险信息)
二、控制模块
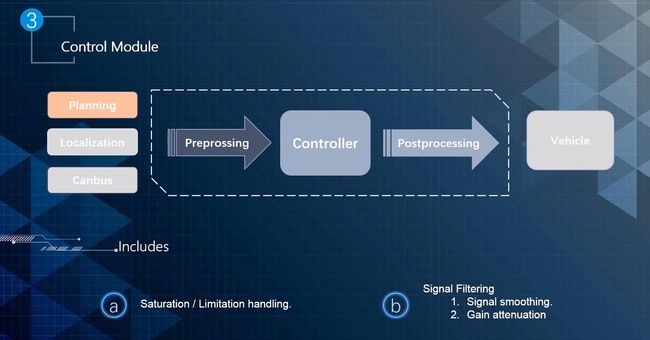
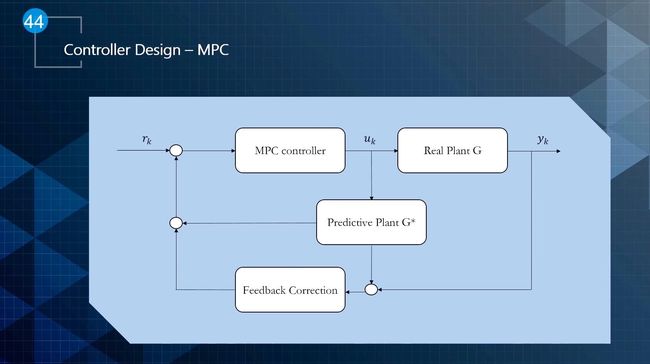
如下图所示,控制模块包括三个部分:预处理、控制器和后处理。
其中,预处理部分的主要功能:
后处理部分功能:
三、控制的作用
控制主要是为了弥补数学模型和物理世界执行之间的不一致性。对于自动驾驶而言,规划的轨迹和车辆的实际运行轨迹并不完全一致,控制器按照规划轨迹在条件允许下尽可能地调节车辆本身。
四、控制的性能要求
- 准确性,应尽量避免偏离目标轨迹,保证行车的安全性。
- 可行性,在现实中要能够实现。
- 平稳度,最大限度地提供乘客的舒适度。要使控制顺利进行,驱动必须是连续的,应避免突然转向、加速或制动。
控制是驱使车辆前行的策略。控制器使用一系列路径点来接收轨迹。并使用控制输入(转向、加速和制动等)让车辆通过这些路径点。
![]()
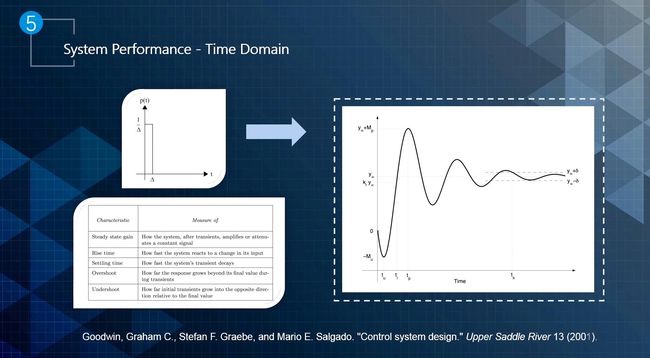
具体而言,自动驾驶系统是否满足性能要求可以从三个角度去评测:时域、频域以及discrete domain(离散域)。
- 时域是指输出在时间轴上应该满足的要求。其衡量的指标包括steady state gain、rising time、setting time、overshoot和undershoot。每个指标对应的具体含义如下图所示。
- 在频域空间,X轴是输入频率,Y轴是输出跟输入的比例,理想状态下输出和输入比例应该为1。系统性能在频域中的评价指标包括pass band、cutoff frequency等,如下图所示。
基于模型的控制方法
一、建模
Modeling一般可以分为分析建模和拟合建模。通常,一个模型主要由各种属性表示,如下图所示:
- 运动学模型是一种几何模型,感知、预测讨论的模型则以运动学模型为主。
- 而在控制模块中,更多考虑动力学模型。实际上,运动学模型是动力学模型的一个子集。
在自动驾驶中,Dynamic model以Kinematics model为初始模型,将环境等参数设置到Kinematics model中,把车看作质点进行分析。Dynamic model 将车按车轮等部分分开进行约束或者系统补偿。

两个比较简单的几何模型:下图左边是一个综合移动机器人控制模型,右边是著名的自行车模型,它把汽车看作只有两个轮胎的自行车,该模型在当年的DARPA挑战赛上获得冠军。

实际上,只考虑几何约束是不够的。下图是一个动力学模型,它不仅考虑了几何约束,还考虑了力矩和扭矩平衡。在自行车模型中,把前后轮都在XY两个方向进行分解。

下图是刚体的一些力矩分析以及扭矩分析的公式,总体满足牛顿第二定律。

通常情况下,模型的建立是基于误差,而不是参考值,如下图所示,对实际侧向加速度和理想侧向加速度之间的误差进行建模。
二、系统辨识
在模型中,有些参数是未知的,系统辨识的目的是确定这些未知参数的值。确定未知参数的方法有三种:白盒、灰盒以及黑盒方法。
三、控制器设计
基于模型的控制模块设计第三步是控制器的设计,包括滤波器设计、控制器设计以及观察器设计等。
1、滤波器设计
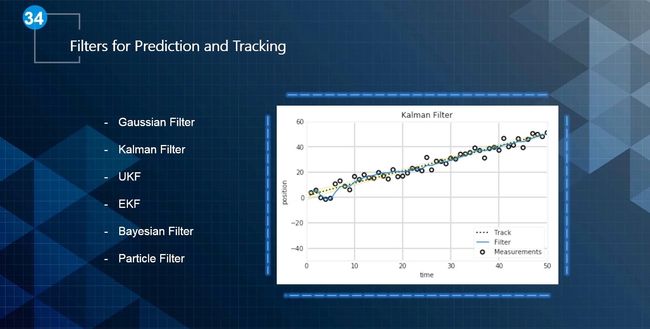
滤波器的分类:
2、控制器设计
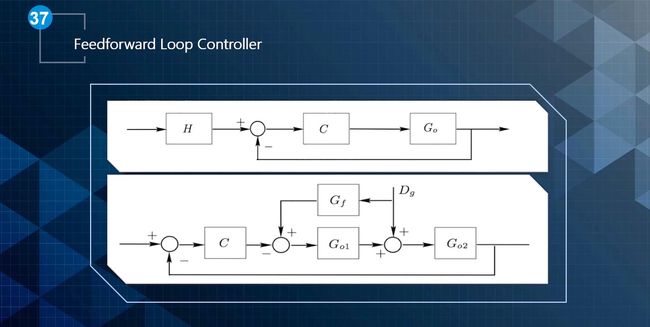
控制器的类型大致可以分为三类,分别是开环控制、前馈环控制和后馈环控制,如下图所示。
- 前馈环控制器可以分为两类,如下图所示:
- 上图是增加一个H(前置滤波器),把输入转化为理想的输入。
- 下图是把扰动量加入到前馈环中,将模型的先验知识添加到环路,减少扰动的影响。
前馈环控制器的主要控制策略:
Deadzone主要是执行器的一些特性引起的,例如汽车的油门,可能给油0%~15%的区间都不会使汽车前行,这个时候反应在图上就是一条平行的线段,即Deadzone。在控制器设计的时候需要对这部分进行补偿设计,如下图所示:
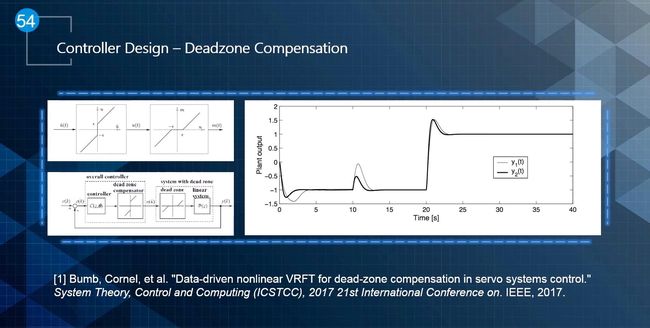
饱和和抗饱和处理也是出于对执行器的特性的考虑,通常一个执行器是有上限和下限的,如下图所示,把输出值做一个限制,使得输出在执行器的上下限范围内。如果不进行饱和处理,在输出100%的情况下突然转换状态,收敛到最终值可能需要很长的时间。
- 控制器的发展趋势:
四、参数调优
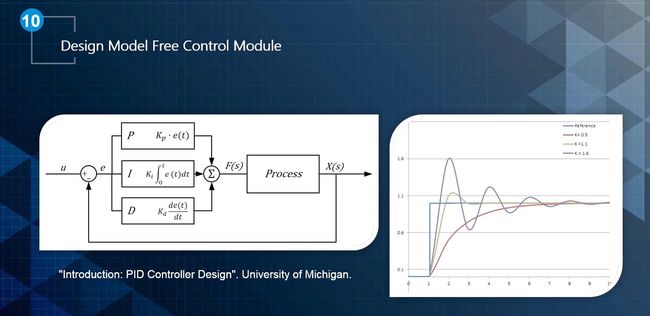
1、PID控制
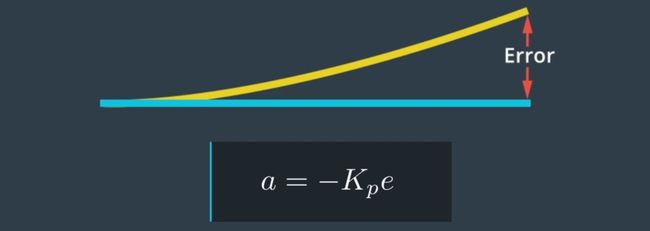
- P(比例Proportional):P控制器在车辆开始偏离时立即将其拉回目标轨迹。车辆偏离越远,控制器越难将其拉回目标轨迹。当kp比较小的时候,接近终值的速度会非常慢,没有超调(红线);当kp设置比较大时(紫线),则达到稳态速度变快,但会超调。
- D(微分Derivative):增加了一个阻尼项,可最大限度地减少控制器输出的变化速度,使运动处于稳定状态。微分控制的目的是使系统更快的从瞬态转化为稳态。
- I(积分Integral):控制器会对系统的累积误差进行惩罚,负责纠正车辆的任何系统性偏差(如转向失准)。如果系统中存在损耗,比如汽车上坡的动力或者摩擦损耗,使得比例控制每次增加的控制量就等于或者小于损耗时,出现稳态误差,这就是引入积分控制的目的,它可以将之前的误差进行积分,消除稳态误差。
- 优点:非常简单,具有通用性。只需要知道车辆与目标轨迹有多大的偏离,在很多情况下的效果很好。
- 缺点:PID控制器只是一种线性算法,对于非常复杂的系统而言,这是不够的。除此之外,PID控制器依赖于实时误差测量,这意味着测量延迟时可能会失效。
2、线性二次调节器(LQR)
- 集合X:捕获车辆的状态,包含横向误差、横向误差的变化率、朝向误差和朝向误差的变化率。
- 集合U:控制输入包括转向、加速和制动。
- L(线性):线性控制的模型如下图的等式所示,表示x点是如何受当前状态 x 和控制输入 u 的影响的。
- Q(二次项):为了让误差最小化且尽可能少地使用控制输入,我们让x和u与自身相乘,这样负值也会产生正平方,这就是二次项。然后为这些项分配权重并全部相加。
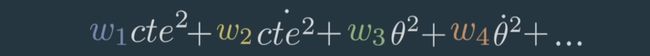
最优的u应该最小化二次项的和在时间上的积分,数学中将这个积分值称为成本函数,如下图所示。Q和R代表x和u的权重集合,每个矩阵与自身相乘。
Apollo在LQR中的控制方法被描述为u=-Kx,许多工具都可以轻松地用来解决K。
3、模型控制预测(MPC)
- 建立车辆模型。该模型估计了假如将一组控制输入应用于车辆时会发生的结果,即MPC 预测未来 的能力,需要在准确度与快速性之间做出取舍。
- 将模型发送到搜索最佳控制输入的优化引擎,通过搜索密集数学空间来寻求最佳解决方案。为缩小搜索范围,优化引擎依赖于车辆模型的约束条件,可通过自定义的成本函数(如下图所示)对轨迹进行评估。
- 执行第一组控制输入。
因为是近似测量与计算,控制器实际上只实现了序列中的第一组控制输入。 MPC是一个重复过程,在每个时间步不断地重新评估控制输入的最优序列。
- 优点:考虑了车辆模型,所以比PID控制更精确;适用于不同的成本函数,所以我们可以在不同情况下优化不同的成本。
- 缺点:MPC相对更复杂、更缓慢、更难以实现,但是值得投入成本研究。

MPC的代价函数如下图所示。从图中可以看出,代价函数增加了约束边界,有上边界和下边界。
4、自适应控制
5、鲁棒性控制(Robust Control)
鲁棒性用来解决如何确定模型的正确性问题。它主要是用来处理模型的非确定性,是一种在已知模型错误边界的情况下,设计一个性能不错而且稳定的控制器的方法。最简单的鲁棒性控制器是LQR/LTR控制器,也是一个二次线性调节器,如下图所示。
6、离散化
离散化实际上是在尽可能的保存连续空间信息的情况下,把连续空间的问题转换为离散空间的描述,使得计算机能够更好地处理。需要注意的是离散化跟Digital Stability是相关的,如果采样不够好,会丢失很多信息使得系统不稳定。
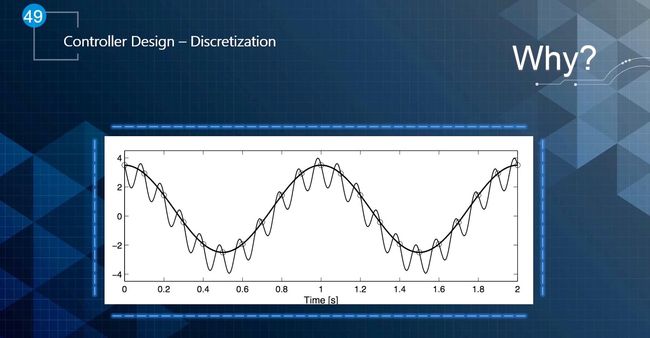
离散化有很多的方法,各种方法都有各自的优缺点。但是总的来说都是把数字信号转换为模拟输入/输出信号,如下图所示:

左边是时域里的函数performance的表达方式,右边是进行离散化的一些常用表达形式。最后一列是收敛的速率,表示在一定工况下,数字控制器在给定的时间下是可以保证收敛的。
工程应用
目前,在Apollo中,控制的工程应用主要有两个方面: