初步了解TensorFlow如何实现自定义损失函数

我们知道，在预测商品销量时，如果预测多了（预测值比真实销量大），商家损失的是生产商品的成本；而如果预测少了（预测值比真实销量小），损失的则是商品的利润。因为一般商品的成本和商品的利润不会严格相等，比如如果一个商品的成本是1元，但是利润是10元，那么少预测一个就少挣10元；而多预测一个才少挣1元，所以如果神经网络模型最小化的是均方误差损失函数，那么很有可能此模型就无法最大化预期的销售利润。

为了最大化预期利润，需要将损失函数和利润直接联系起来，需要注意的是，损失函数定义的是损失，所以要将利润最大化，定义的损失函数应该刻画成本或者代价，下面的公式给出了一个当预测多于真实值和预测少于真实值时有不同损失系数的损失函数：

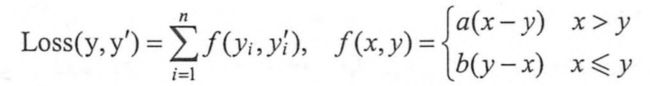
其中，yi为一个batch中第i个数据的真实值，yi’为神经网络得到的预测值，a和b是常量，比如在上面介绍的销量预测问题中，a就等于10 （真实值多于预测值的代价），而b等于1 （真实值少于预测值的代价）。

通过对这个自定义损失函数的优化，模型提供的预测值更有可能最大化收益，在TensorFlow中，可以通过以下代码来实现这个损失函数：

loss = tf.reduce_sum(tf.where(tf.greater(y_, y), (y_ - y) * loss_less, (y - y_) * loss_more))

1. tf.greater函数的输入是两个张量，此函数会比较这两个输入张量中每一个元素的大小，并返回比较结果，当tf.greater的输入张量维度不一样时，TensorFlow会进行类似NumPy广播操作（broadcasting）的处理；

2. tf.where函数有三个参数，第一个为选择条件，当选择条件为True时，tf.where函数会选择第二个参数中的值，否则使用第三个参数中的值，需要注意的是，tf.where函数的判断和选择都是在元素级别进行的。

接下来使用一段TensorFlow代码展示这两个函数的使用：

import tensorflow as tf

v1 = tf.constant([1.0, 2.0, 3.0, 4.0])
v2 = tf.constant([4.0, 3.0, 2.0, 1.0])

with tf.Session() as sess:
    print(sess.run(tf.greater(v1, v2)))
    print(sess.run(tf.where(tf.greater(v1, v2), v1, v2)))
    '''输出结果为：
    [False False  True  True]
    [4. 3. 3. 4.]'''

在了解如何使用这两个函数之后，我们来看一看刚才的预测商品销售量的实例如何通过具体的TensorFlow代码实现：

import tensorflow as tf
from numpy.random import RandomState

#声明wl、W2两个变量，通过seed参数设定了随机种子，这样可以保证每次运行得到的结果是一样的
w = tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))

x = tf.placeholder(tf.float32, shape=(None, 2), name="x-input")
y_ = tf.placeholder(tf.float32, shape=(None, 1), name="y-input")

#定义神经网络结构
y = tf.matmul(x, w)

#定义真实值与预测值之间的交叉熵损失函数，来刻画真实值与预测值之间的差距
loss_less = 10
loss_more = 1
loss = tf.reduce_sum(tf.where(tf.greater(y_, y), (y_ - y) * loss_less, (y - y_) * loss_more))

#定义反向传播算法的优化方法
train_step = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss)

#设置随机数种子
rdm = RandomState(seed=1)
#设置随机数据集大小
dataset_size = 128
X = rdm.rand(dataset_size, 2)
'''设置回归的正确值为两个输入的和加上一个随机量。
之所以要加上一个随机量是为了加入不可预测的噪音，否则不同损失函数的意义就不大了，因为不同损失函数都会在能完全预测正确的时候最低。
一般来说噪音为一个均值为0的小量，所以这里的噪音设置为-0.05——0.05的随机数。'''
Y = [[x1 + x2 + rdm.rand()/10.0 -0.05] for x1,x2 in X]

#创建会话
with tf.Session() as sess:
    #初始化变量
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    
    print(sess.run(w))
    
    #设置batch训练数据的大小
    batch_size = 8
    #设置训练得轮数
    STEPS = 5000
    for i in range(STEPS):
        #每次选取batch_size个样本进行训练
        start = (i * batch_size) % dataset_size
        end = min(start + batch_size, dataset_size)

        #通过选取的样本训练神经网络并更新参数
        sess.run(train_step, feed_dict={x:X[start:end], y_:Y[start:end]})
    
    print(sess.run(w))
    '''输出结果为：
    [[-0.8113182]
 	 [ 1.4845988]]
	[[1.019347 ]
 	 [1.0428089]]'''

可以看到参数w优化后，预测函数为1.019347 * x1 + 1.0428089 * x2，显然是大于实际的预测函数x1 + x2的，这是因为我们的损失函数中指定预测少了的损失更大（loss_less > loss_more），所以模型会偏向于预测多一点。

如果我们更换代码，改为：

loss_less = 1
loss_more = 10

那么我们的结果就会变为：

[[-0.8113182]
 [ 1.4845988]]
[[0.95561105]
 [0.98101896]]

预测函数变为了0.95561105 * x1 + 0.98101896 * x2，可以看到这时候模型就会偏向于预测少一点。

因此，我们可以得出结论：对于相同的神经网络，不同的损失函数会对训练得到的模型产生不同效果。