单调栈 / 单调队列
单调栈 / 单调队列
- 一、单调栈
-
- 模板
- 1、 Leetcode 155. 最小栈 (简单)
- 2、Leetcode 496. 下一个更大元素 I (简单)
- 3、 Leetcode 739. 每日温度(中等)
- 4、Leetcode 42. 接雨水(困难)
- 二、单调队列
-
- 模板
- 1、 Leetcode 剑指 Offer 59 - II. 队列的最大值(中等)
- 2、 Leetcode 239. 滑动窗口最大值 (困难)
一、单调栈
简单来说就是维护一个栈,使得该结构内的元素是单调递增 / 单调递减 / 单调不增 / 单调不减(递增和不增的差别在于是否包括等于的情况)。总的来说还是一个辅助栈,现通过一些题目进行分析:
- Leetcode 155. 最小栈 (简单)
- Leetcode 496. 下一个更大元素 I (简单)
- Leetcode 739. 每日温度(中等)
- Leetcode 42. 接雨水(困难)
模板
stack<int> stack; //单调栈
for (遍历待操作序列) {
while (栈非空 && 栈顶和当前元素满足指定的大小关系) {
获得题目要求的东西;
stack.pop(); //出栈
}
stack.push(i); //压入索引
}
1、 Leetcode 155. 最小栈 (简单)
题目
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。
示例
输入:
[“MinStack”,“push”,“push”,“push”,“getMin”,“pop”,“top”,“getMin”]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
提示
pop、top 和 getMin 操作总是在 非空栈 上调用。
思路
总的来说,这道题其实就是要使得得到目前栈中最小值的时间复杂度为O(1),那么可以开一个单调栈存下每个阶段的最小值,需要的时候返回单调栈的栈顶即可。
但这个不太好讲,直接讲例子吧:对于[ 4、7、2、6、8、2 ],我们开两个栈,nums - 依次放所有元素、help - 辅助栈(单调栈)。
一开始遇到 4,两个栈都为空,那么都压栈,得到:nums{ 4 ➡},help{ 4 ➡};
遇到 7,肯定会压入nums,但是因为 7 比help栈顶大,所以不压入help,得到:nums{ 4,7➡},help{ 4 ➡};
遇到 2 ,因为 2 不比help栈顶大,所以两个栈都压入,得到:nums{ 4,7,2 ➡},help{ 4,2 ➡};
遇到 6 ,同理,压入nums,不压help,得到:nums{ 4,7,2,6 ➡},help{ 4 ,2➡};
遇到 8,同理,压入nums,不压help,得到:nums{ 4,7,2,6,8 ➡},help{ 4 ,2➡};
遇到 2,因为 2 不会大于help栈顶,所以两个栈都压入,得到:nums{ 4,7,2,6 ,2➡},help{ 4,2,2➡}。
那么此时,如果要出栈,nums必定出栈,但假如nums出栈的元素刚好等于help栈顶,则help也要出栈,避免下一次getMin() 得到的元素在nums里面不存在。
而getMin函数,直接返回help的栈顶,因为help记录了每个状态当前所在最小值。
class MinStack {
public:
/** initialize your data structure here. */
stack<int> nums, help; //nums-放所有元素 help-辅助栈/单调栈
MinStack() {
}
void push(int x) {
nums.push(x);
if (help.empty()) help.push(x);
else if (x <= help.top()) help.push(x);
}
void pop() {
int x = nums.top();
if (help.top() == x) help.pop();
nums.pop();
}
int top() {
return nums.top();
}
int getMin() {
return help.top();
}
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(x);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->getMin();
*/
2、Leetcode 496. 下一个更大元素 I (简单)
题目
给你两个没有重复元素的数组 nums1 和 nums2 ,其中nums1 是 nums2 的子集。
请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出 -1 。
示例
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
对于 num1 中的数字 4 ,你无法在第二个数组中找到下一个更大的数字,因此输出 -1 。
对于 num1 中的数字 1 ,第二个数组中数字1右边的下一个较大数字是 3 。
对于 num1 中的数字 2 ,第二个数组中没有下一个更大的数字,因此输出 -1 。
提示
1 <= nums1.length <= nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 10^4
nums1和nums2中所有整数 互不相同
nums1 中的所有整数同样出现在 nums2 中
思路
先不管nums1数组,先把nums2数组里面每一个元素的 “ 下一个更大元素 ” 找出来,记录在哈希表或者数组里面,再去遍历nums1得到最终结果。
通过题意我们可以发现,假如nums2里面的两个相邻元素a、b是递增的,那么第二个元素 b 就是第一个元素 a 的 “ 下一个最大元素 ”;反之,如果两个相邻元素非递增(递减 / 相等(但是题目已经说了没有重复元素,所以相等的情况我们无须考虑)),则还得看接下来有没有出现 一个数比 a 大,如果有,则它是 a 的 “ 下一个最大元素 ”,反之返回 - 1。
无疑,如果每一次 a b 非递增都去往后找是非常浪费时间的,那么此时我们可以开一个单调栈来维护那些暂时得不到 “下一个最大元素” 的 a,使得该栈一直保持从栈顶到栈底单调不减,直到遇到合适的就把它弹出。
举个例子nums2 = [ 7,4,6,5,9,20 ],一开始先把 7 压栈,遍历到 4 ,发现 4 比栈顶小,再压栈,使得现在栈为:{7,4 ➡}。然后走到 6 ,发现 6 比 栈顶的 4 大,说明 6 是 4 的 “ 下一个最大元素 ”,记录下 “4 - 6”,但是此时的栈顶为 7,7 > 6,不满足要求,继续把 6 压栈得到:{7,6➡}。以此类推,先把 5 压栈,遇到了 9
,发现 9 一直把栈顶大,所以一直弹出直到栈空,得到对应关系:5 - 9、6 - 9、7 - 9。然后 9 压栈,走到20 的时候,9 出栈得到 9 - 20。但此时 20 没有数可以与它配对,所以 20 对应 - 1。
在此期间可以发现,栈里面的元素自栈顶到栈底是单调递增的,所以说该栈为单调栈。说白了其实就是一个栈,只不过栈中元素自顶到底有单调性,起到辅助作用。
class Solution {
public:
int book[10010]; //存下每一个数的对应关系,比如 4 - 9,则为book[4] = 9
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
int i, length = nums2.size();
for (i = 0; i < 10010; ++ i) book[i] = -1; //初始化为 - 1,不能为0
stack<int> stack; //单调栈
stack.push(nums2[0]);
for (i = 1; i < length; ++ i) {
if (nums2[i] > nums2[i - 1]) {
while(! stack.empty() && stack.top() < nums2[i]) { //找到“下一个最大元素”
book[stack.top()] = nums2[i];
stack.pop();
}
}
stack.push(nums2[i]);
}
length = nums1.size();
vector<int> ans;
for (i = 0; i < length; ++ i)
ans.push_back(book[nums1[i]]);
return ans;
}
};
3、 Leetcode 739. 每日温度(中等)
题目
请根据每日 气温 列表,重新生成一个列表。对应位置的输出为:要想观测到更高的气温,至少需要等待的天数。如果气温在这之后都不会升高,请在该位置用 0 来代替。
例如,给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73],你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
提示
气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度,都是在 [30, 100] 范围内的整数。
思路
这一道题和上一道的 [ 2、Leetcode 496. 下一个更大元素 I ] 差不多,思路是一样的。
区别就在于,这一道题要的是间隔天数,而不是下一个更高温度是几度。所以如果和上一道题一样,弹出到比栈顶小或等于就停下,那么会导致间隔天数变少了。
一开始我不知道要怎么处理,而且题目提示了日温在 30 ~ 100之间,但是温度列表的长度在1 ~ 30000,所以会有重复的日温,所以不能像第二题那样开数组或者哈希表存对应关系。
但其实,仔细想想,要想得到当日气温和更高气温的间隔天数,只要这两天对应的索引一减就可以了。所以对于单调栈来说,压入的是索引,而不是温度。
举个例子,对于题目给的样例 temperatures = [73, 74, 75, 71, 69, 72, 76, 73],开一个单调栈stack。
先压入 0(73的索引)。
遇到 74 的时候,发现 74 比栈顶对应的温度大,先把栈顶出栈,此时再通过 ans[stack.top()] = i - stack.top(); 就能获得间隔天数并对ans(最终返回的vector)赋值。
其他操作和第二题无异。
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& T) {
int length = T.size();
vector<int> ans(length, 0);
stack<int> stack; //单调栈
for (int i = 0; i < length; ++ i) {
while (! stack.empty() && T[i] > T[stack.top()]) {
ans[stack.top()] = i - stack.top();
stack.pop();
}
stack.push(i); //压入索引
}
return ans;
}
};
4、Leetcode 42. 接雨水(困难)
题意
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
思路
这道题首先明确的是,要想盛水,那么必定是两边高、中间低的情况,如果只有递减或者递增则不满足要求。
那么我们现在开一个单调栈,把不增(即递减或相等)部分的索引存下来,直到遇到一个比栈顶对应值高的元素,就去判断是否能构成 “ 高低高 ” ,若能则累计盛水量。
一开始我一直钻牛角尖,总是想要在当前元素 > 栈顶元素的时候,分类去讨论得到的雨水,但总是算漏或者多算,wa了好久……
但其实想想,单调栈单调栈,不就是想占它单调的便宜吗?如果只是拿来比较当前元素和栈顶,似乎开不开单调栈也不是特别重要。但是单调栈本身就已经使得 “ 高低高 ” 的 “ 高低 ” 可以得到满足,只需要另外一个 “ 高 ” 的到来,就可以盛雨水了。
当然,这道题的单调栈只是单调不增,还可能存在 “ 低低高 ”,所以我是先记录了还没出栈前的栈顶元素(虽然只是得到索引,但可得到对应的高度),再弹出栈,如果接下来栈顶元素对应的高度一直和原先记录的高度一致,那么一直出栈,直到遇到 “ 高低高 ” 的左边那个高为止。
假如出栈操作结束后,栈不空,说明构成了 “高低高”,反之是 “低低高”。
class Solution {
public:
int trap(vector<int>& height) {
int length = height.size(), cnt = 0;
stack<int> stack;
for (int i = 0; i < length; ++ i) {
while (! stack.empty() && height[i] > height[stack.top()]) {
int mid = stack.top(); //高度夹在中间的索引
while (!stack.empty() && height[stack.top()] == height[mid])
stack.pop(); //假如是 4 2 2 5,那么中间的两个 2 可以一起算
if (! stack.empty()) //非空说明可以构成高低高,避免是 2 2 5的情况
//能盛水的矩形的高 = 次高 - 最低,长 = 最有索引 - 最左索引 - 1
cnt += (min(height[stack.top()], height[i]) - height[mid]) * (i - stack.top() - 1);
}
stack.push(i);
}
return cnt;
}
};
二、单调队列
- Leetcode 剑指 Offer 59 - II. 队列的最大值(中等)
- Leetcode 239. 滑动窗口最大值 (困难)
模板
deque<int> help;
for(遍历待操作序列) {
//维护单调队列
while (队列非空 && 队首和当前元素大小关系)
help.pop_back();
help.push_back(当前元素);
//题目要求的操作
…………
}
1、 Leetcode 剑指 Offer 59 - II. 队列的最大值(中等)
题目
请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
若队列为空,pop_front 和 max_value 需要返回 -1
示例 1
输入:
[“MaxQueue”,“push_back”,“push_back”,“max_value”,“pop_front”,“max_value”]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]
示例 2
输入:
[“MaxQueue”,“pop_front”,“max_value”]
[[],[],[]]
输出: [null,-1,-1]
限制
1 <= push_back,pop_front,max_value的总操作数 <= 10000
1 <= value <= 10^5
思路
简单来说和上面那个最小栈差不多,这道题需要开一个双端队列来充当辅助队列,作用在于双端队列队首是操作队列当前的最大值,其本身从队首到队尾单调不增。
例如对于4,2,8,9,0,7,2
nums:4 【 help:4】
nums:4,2 【 help:4,2】
nums:4,2,8 【help:8】
nums:4,2,8,9 【 help:9】
nums:4,2,8,9,0 【 help:9,0】
nums:4,2,8,9,0,7 【help:9,7】
nums:4,2,8,9,0,7,2 【 help:9,7,2 】
如果nums有出队,出队的元素与help的队首相等,那么help的队首也要出队。
class MaxQueue {
public:
queue<int> nums; //暂且叫它操作队列吧,不知道怎么命名好 害
deque<int> help; //双端队列
MaxQueue() {
}
//获得当前最大值
int max_value() {
if (nums.empty()) return -1;
return help.front();
}
//入队
void push_back(int value) {
while (! help.empty() && value > help.back())
help.pop_back();
nums.push(value);
help.push_back(value);
}
//出队
int pop_front() {
if (nums.empty()) return -1;
int a = nums.front();
nums.pop();
if (help.front() == a) help.pop_front();
return a;
}
};
/**
* Your MaxQueue object will be instantiated and called as such:
* MaxQueue* obj = new MaxQueue();
* int param_1 = obj->max_value();
* obj->push_back(value);
* int param_3 = obj->pop_front();
*/
2、 Leetcode 239. 滑动窗口最大值 (困难)
题目
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
示例 1
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
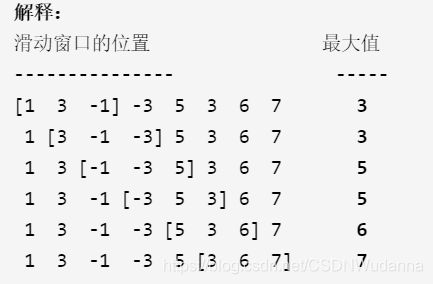
示例 2
输入:nums = [1], k = 1
输出:[1]
示例 3
输入:nums = [1,-1], k = 1
输出:[1,-1]
提示
1 <= nums.length <= 10 ^ 5
-10 ^ 4 <= nums[i] <= 10 ^ 4
1 <= k <= nums.length
思路
和其他题差不多。
//单调队列
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
deque<int> help;
int length = nums.size();
//先放前k个
for (int i = 0; i < k; ++ i) {
while (!help.empty() && nums[i] > help.back())
help.pop_back();
help.push_back(nums[i]);
}
vector<int> ans;
ans.push_back(help.front());
for (int i = k; i < length; ++ i) {
//假如最左边那个即将离开窗口的数是当前最大值,那么需要弹出help队首
if(help.front() == nums[i - k])
help.pop_front();
//维护单调队列
while (!help.empty() && help.back() < nums[i])
help.pop_back();
help.push_back(nums[i]);
//得到当前窗口最大值-->队首
ans.push_back(help.front());
}
return ans;
}
};
