泛型容器-红黑树源码分析附带详细图解

红黑树介绍

1.2-3树

红⿊树是⼀种⾃平衡的⼆叉树，它可以避免⼆分搜索树在极端的情况下蜕化成链表的情况。那么什么是红⿊树呢？要想便于了解红⿊树，我们先了解⼀下跟它息息相关的2-3树。

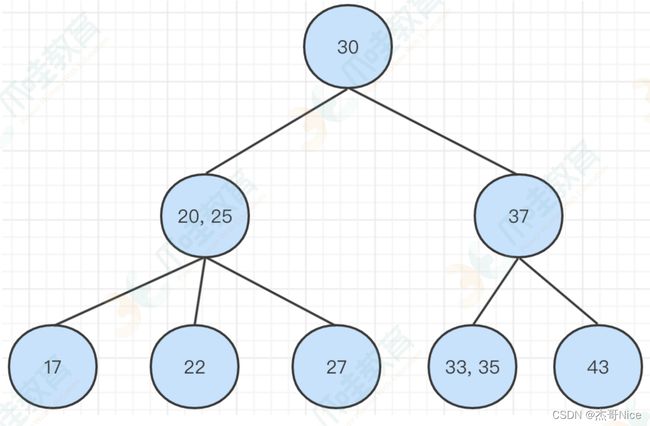
2-3树是⼀种绝对平衡的多叉树，在这棵树中，任意⼀个节点，它的左右⼦树的⾼度是相同的。如下所示：

正如上⾯介绍过的，2-3树是⼀个多叉树。那为什么叫做2-3树呢？ 因为规则定义，2-3树分为两种节点，分别为：2-节点和3-节点。其中，2-节点表示节点中保存⼀个元素，3-节点则表示节点中保存两个元素。

• 演示⼀下如何⽣成⼀个2-3树：
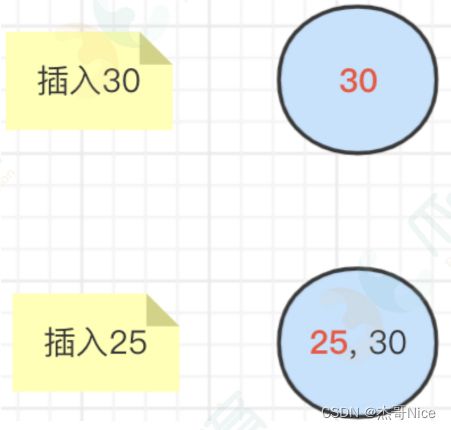
  • ⾸先：向2-3树中插⼊30和25

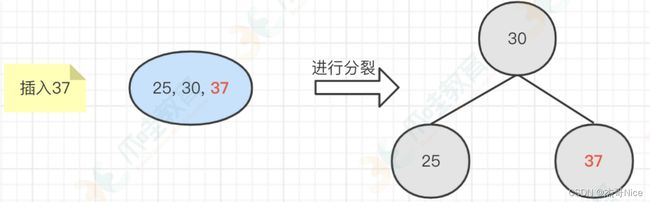
• • 当再插⼊37的时候，⼀个节点就容纳了3个元素了，那么就要进⾏分裂操作了，如下所示：

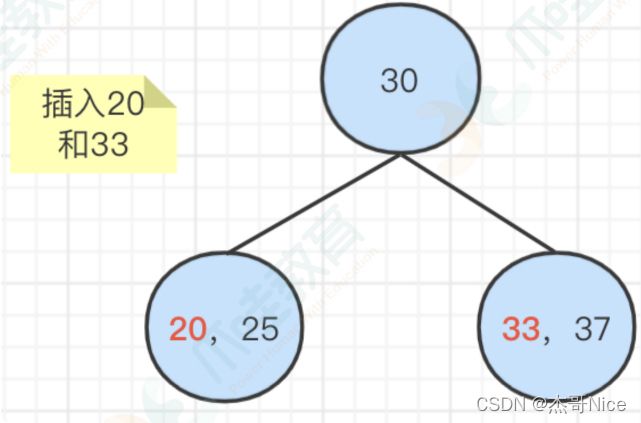
• • 然后，我们再插⼊20和33，可以正常的容纳这两个元素

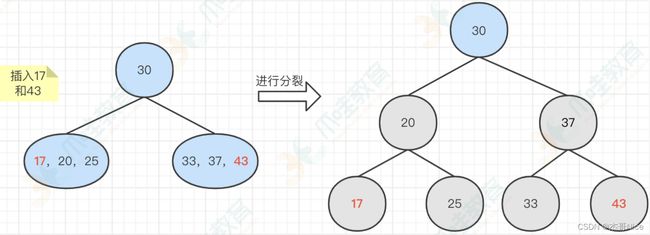
• • 我们再继续插⼊17和43，那么出现了两个节点都分别容纳了3个元素，那么这两个节点都需要进⾏分裂操作了

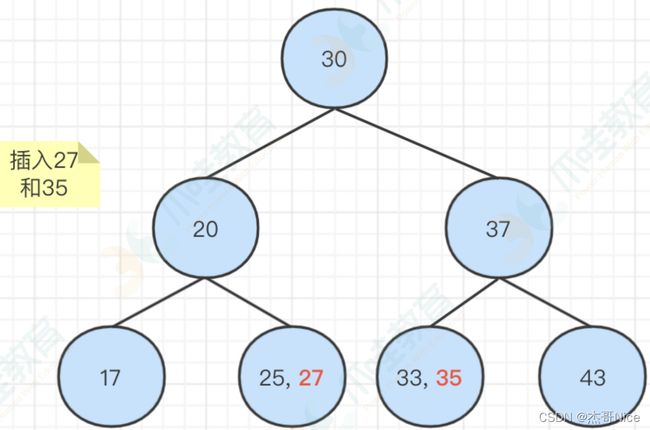
• • 插⼊27和35，两个节点都可以容纳这两个新插⼊的元素

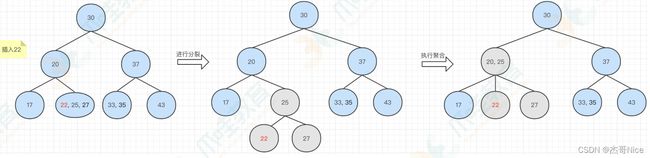
• • 那么再最后插⼊22，结果发现，⼀个节点容纳了3个元素，要进⾏分裂，但是分裂后，叶⼦节

点的⾼度不⼀致了，那么就要再进⾏聚合操作，如下所示：

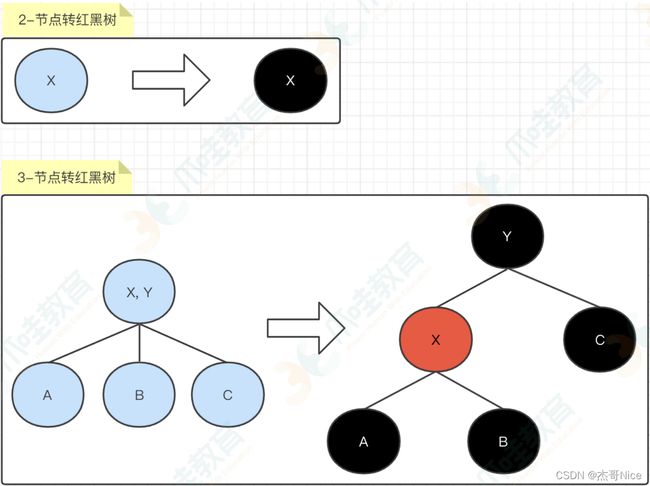
• 那么，我们了解完2-3树之后，我回过头来看⼀下红⿊树，也就是说，2-3树怎么转变成红⿊树呢？⽅式很多，此处我们可以采⽤左倾红⿊树的⽅式，来将2-3树转换为红⿊树，转换规则如下：

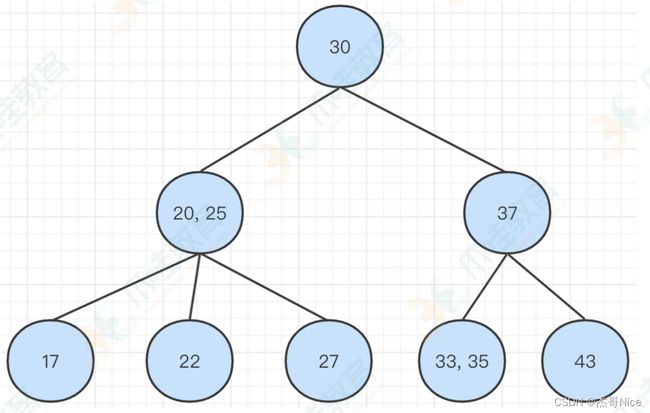
• • 我们可以根据上⾯的转换规则，进⾏转换操作。下图是我们上⾯讲2-3树的时候，构造的。

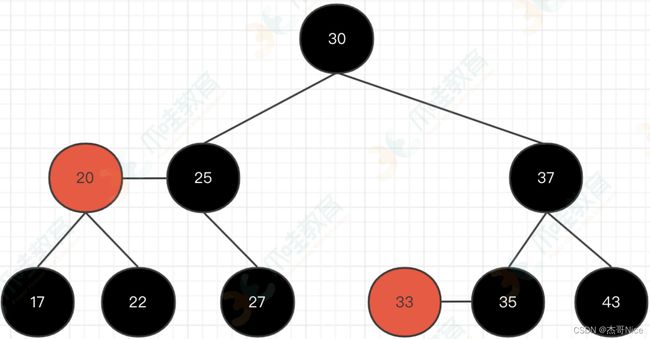
• • 那么我们按照规则进⾏转换，如下所示：

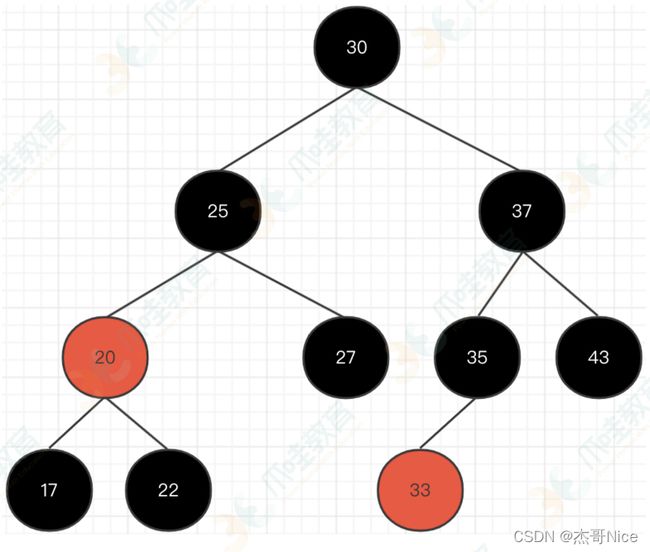
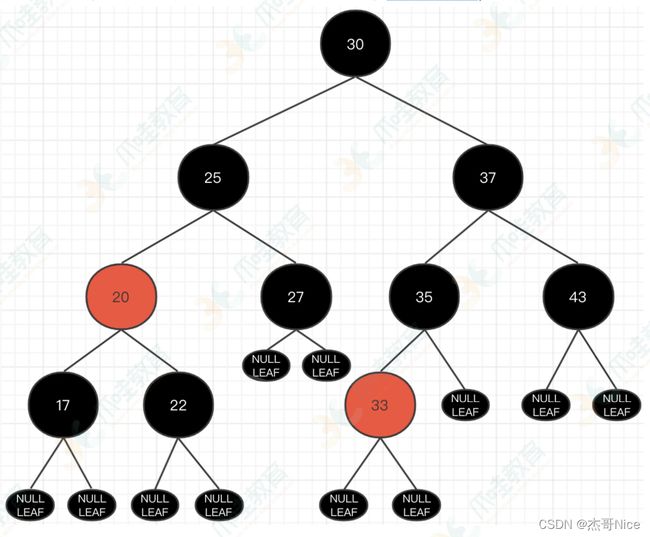
• • 我们按照树形结构进⾏修整，那么就是我们今天要介绍的红⿊树。如下所示：

2.红黑树

• ********组成红黑树的五个必要条件********（面试必问）
  • 条件⼀：每个节点要么是红⾊，要么是⿊⾊。
  • 条件⼆：根节点⼀定是⿊⾊的。
  • 条件三：每个叶⼦节点⼀定是⿊⾊。
  • 条件四：如果⼀个节点是红⾊，那么它的左右⼦节点⼀定都是⿊⾊的。
  • 条件五：从任意⼀个节点到叶⼦节点，所经过的⿊⾊节点的数量⼀样多。
• 完整的红⿊树

一、源码概述

当我们掌握了红⿊树的理论知识之后，下⾯我们就来开始分析HashMap的源码了。那我们从哪⾥开始⼊⼿呢？要回答这个问题，那么就要从我们最常使⽤HashMap的场景出发了。当我们想要是⽤HashMap的时候，我们⾸先会通过HashMap的构造⽅法创建HashMap，然后通过put⽅法向HashMap对象赋值。那么我们就可以通过构造函数+put这两点进⾏源码的切⼊点。

1.1 HashMap的构造函数

• 我们先来看HashMap的构造方法

/**
 * Constructs an empty HashMap with the default initial capacity
 * (16) and the default load factor (0.75).
 */
public HashMap() {
    this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}

通过源码我们可以看到只有⼀⾏代码，即：给loadFactor赋值。

那么loadFactor是什么呢？它是HashMap的加载因⼦，也就是说，元素所占的空间达到加载因⼦的规定值的时候，那么就会

执⾏扩容。

那么初始化加载因⼦的时候，赋值给它DEFAULT_LOAD_FACTOR属性了。

DEFAULT_LOAD_FACTOR这个值是多少呢？我们去源码中寻找答案。

/** * The load factor used when none specified in constructor. */ static final float DEFAULT_LOAD_FACTOR = 0.75f;

/**
 * The load factor used when none specified in constructor.
 */
static final float DEFAULT_LOAD_FACTOR = 0.75f;

通过上⾯截图，我们知道了，加载因⼦默认被赋值为0.75f，那么其实⼤部分同学都是知道HashMap的结构在JDK8之前是【数组+链表】，⽽从JDK8之后，存储结构就变为了【数组+链表+红⿊树】了。那么这个0.75的含义就是：如果数组中存储的元素⻓度达到了原⻓度的75%或者3/4的话，那么就需要执⾏扩容操作了。

构造函数就这么⼀⾏代码，即：给loadFactor赋值为0.75f。是不是很简单。那我们看完了构造函数的代码，我们就来把视⻆转到put⽅法吧。

1.2 put方法

public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}

• put⽅法⾥⾯，只是调⽤了putVal⽅法，如下是putVal⽅法：

/**
 * Implements Map.put and related methods.
 *
 * @param hash         key的哈希值
 * @param key          key值
 * @param value        value值
 * @param onlyIfAbsent 如果是true,则不改变已存在的value值
 * @param evict        驱逐，赶出，逐出 if false, the table is in creation mode.
 *
 * @return previous value, or null if none
 */
// eg1: hash=0 key=0 value="a0" onlyIfAbsent=false evict=true
// eg2: hash=1 key=1 value="a1" onlyIfAbsent=false evict=true
// eg3: hash=16 key=16 value="a16" onlyIfAbsent=false evict=true
// eg4: hash=32 key=32 value="a32" onlyIfAbsent=false evict=true
// eg5: 由于执行步骤与eg4相似，故略过。
// eg6: hash=128 key=128 value="a128" onlyIfAbsent=false evict=true
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
    Node[] tab;
    Node p;
    int n, i;

    // eg1: table=null
    // eg2: table是长度为16的Node数组，且table[1]=Node(1, 1, "a1", null)
    // eg3: table是长度为16的Node数组，且table[1]=Node(1, 1, "a1", null) ... table[6]=Node(6, 6, "a6", null)
    // eg4: table是长度为16的Node数组，且table[1]=Node(1, 1, "a1", null) ... table[6]=Node(6, 6, "a6", null)
    // eg6: table是长度为16的Node数组，且table[1]=Node(1, 1, "a1", null) ... table[6]=Node(6, 6, "a6", null)
    /** 如果是空的table，那么默认初始化一个长度为16的Node数组*/
    if ((tab = table) == null || (n = tab.length) == 0) {
        // eg1: resize返回(Node[]) new Node[16]，所以：tab=(Node[]) new Node[16]， n=16
        n = (tab = resize()).length;
    }

    // eg1: i = (n-1)&hash = (16-1)&0 = 1111&0000 = 0000 = 0; 即:p=tab[0]=null
    // eg2: i = (n-1)&hash = (16-1)&1 = 1111&0001 = 0001 = 1; 即:p=tab[1]=null
    // eg3: i = (n-1)&hash = (16-1)&16 = 1111&10000 = 0000 = 0; 即:p=tab[0]=Node(0, 0, "a0", null)
    // eg4: i = (n-1)&hash = (16-1)&32 = 1111&100000 = 0000 = 0; 即:p=tab[0]=Node(0, 0, "a0", null)
    // eg6: i = (n-1)&hash = (16-1)&128 = 1111&10000000 = 0000 = 0; 即:p=tab[0]=Node(0, 0, "a0", null)
    /** 如果计算后的下标i，在tab数组中没有数据，那么则新增Node节点*/
    if ((p = tab[i = (n - 1) & hash]) == null) {
        // eg1: tab[0] = newNode(0, 0, "a0", null)
        // eg2: tab[1] = newNode(1, 1, "a1", null)
        tab[i] = newNode(hash, key, value, null);
    } else { /** 如果计算后的下标i，在tab数组中已存在数据，则执行以下逻辑 */
        Node e;
        K k;
        // eg3: p.hash==0, hash==16，所以返回false
        // eg4: p.hash==0, hash==32，所以返回false
        // eg6: p.hash==0, hash==128，所以返回false
        if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) { /** 如果与已存在的Node是相同的key值*/
            e = p;
        }
        // eg3: p instanceof Node，所以为false
        // eg4: p instanceof Node，所以为false
        // eg6: p instanceof Node，所以为false
        else if (p instanceof TreeNode) { /** 如果与已存在的Node是相同的key值，并且是树节点*/
            e = ((TreeNode) p).putTreeVal(this, tab, hash, key, value);
        } else { /** 如果与已存在的Node是相同的key值，并且是普通节点，则循环遍历链式Node，并对比hash和key，如果都不相同，则将新的Node拼装到链表的末尾。如果相同，则进行更新。*/
            for (int binCount = 0; ; ++binCount) {
                // eg3: p.next == null
                // eg4-loop1: p.next == Node(16, 16, "a16", null) 不为空
                // eg4-loop2: p.next == null
                /** 获得p节点的后置节点，赋值给e。直到遍历到横向链表的最后一个节点，即：该节点的next后置指针为null */
                if ((e = p.next) == null) {
                    // eg3: p.next = newNode(16, 16, "a16", null);
                    // eg4-loop2: p.next == newNode(32, 32, "a32", null);
                    // eg6: p.next == newNode(128, 128, "a128", null);
                    p.next = newNode(hash, key, value, null);

                    // eg3: binCount == 0
                    // eg4-loop2: binCount == 1
                    /** binCount从0开始，如果Node链表大于8个Node，那么试图变为红黑树 */
                    if (binCount >= TREEIFY_THRESHOLD - 1) {
                        // eg6: tab={newNode(0, 0, "a0", ［指向后面1个链表中的7个node］), newNode(1, 1, "a1", null)}, hash=128
                        treeifyBin(tab, hash);
                    }
                    // eg3: break
                    // eg4-loop2: break
                    break;
                }
                // eg4-loop1: e.hash==16 hash==32 所以返回false
                /** 针对链表中的每个节点，都来判断一下，是否待插入的key与已存在的链表节点相同，如果相同，则跳出循环，并在后续的操作中，将该节点内容更新为最新的插入值 */
                if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) {
                    break;
                }
                // eg4-loop1: p=e=Node(16, 16, "a16", null)
                p = e;
            }
        }

        // eg3: e = null
        // eg4: e = null
        /** 如果存在相同的key值*/
        if (e != null) {
            // egx: String oldValue = "v1"
            V oldValue = e.value;
            // egx: onlyIfAbsent=false
            if (!onlyIfAbsent || oldValue == null) {
                // egx: e = Node(3366, "k1", "v2", null)
                /** 则将新的value值进行更新*/
                e.value = value;
            }
            afterNodeAccess(e);
            // egx: 返回oldValue="v1"
            return oldValue;
        }
    }

    // eg1: modCount==0 ++modCount==1
    // eg2: modCount==1 ++modCount==2
    // eg3: modCount==7 ++modCount==8
    // eg4: modCount==8 ++modCount==9
    ++modCount;

    // eg1: size=0, threshold=12
    // eg2: size=1, threshold=12
    // eg3: size=7, threshold=12
    // eg4: size=8, threshold=12
    if (++size > threshold) {
        resize();
    }
    afterNodeInsertion(evict); /** doing nothing */
    return null;
}

• 代码分解为如下几步：

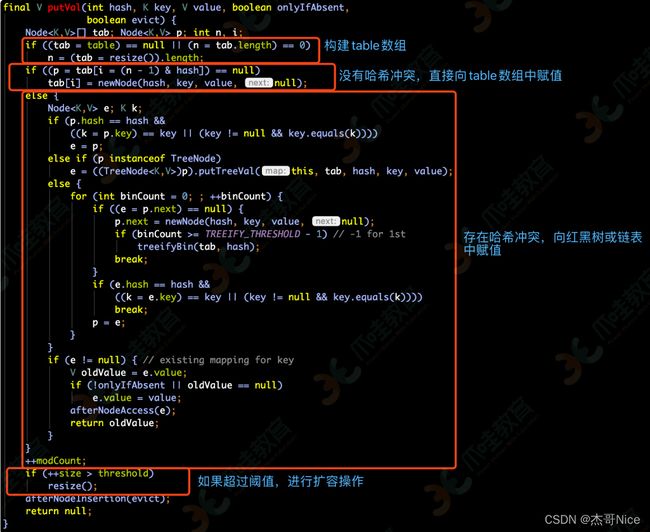
• 正如上⾯源码截图中所描述的，整个putVal⼀共执⾏了三部分内容，分别是：

① 创建table数组

②向table数组中赋值，这⾥⾯分为哈希不冲突和哈希冲突两种情况。

③如果超过阈值，则进⾏扩容操作。

参考文档：JDK1.8 HashMap源码解析+最全面试题_Saintmm的博客-CSDN博客 JDK1.8 HashMap源码解析+最全面试题

图解TreeMap的红黑树平衡操作fixAfterInsertion()，接着手撕红黑树添加节点_Saintmm的博客-CSDN博客 图解TreeMap的红黑树平衡操作fixAfterInsertion()，接着手撕红黑树添加节点

源码干货-put方法源码流程图