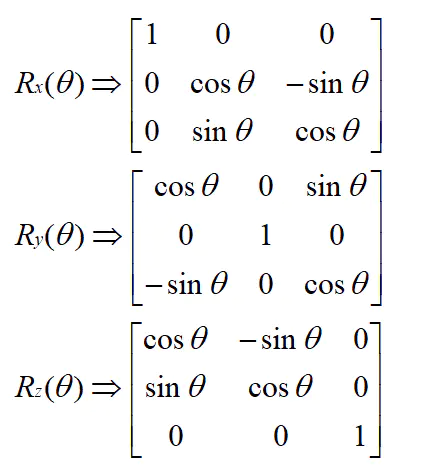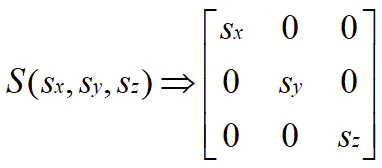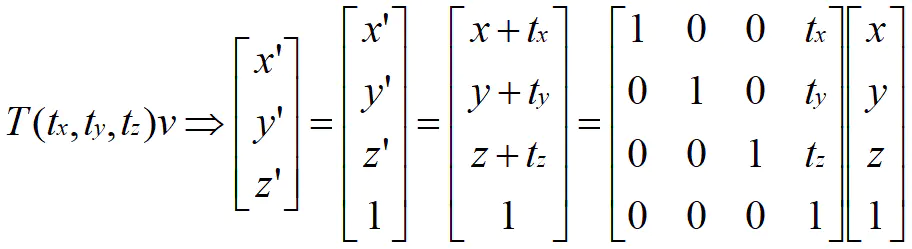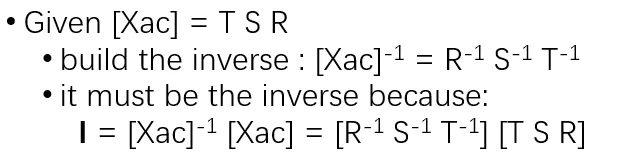变换矩阵_平移 缩放 旋转及统一变换
1. 位移(translation)
对于一个三维坐标(x, y, z),我们想让它往x轴正方向移动1个单位,往y轴正方向移动1个单位,往z轴正方向移动1个单位,则可以让它加上一个向量(1, 1, 1)
2. 旋转(Rotation)
对于一个三维坐标(x, y, z),让其绕x, y, z轴旋转θ角的方法是在其左边乘上一个旋转矩阵。绕x轴,绕y轴,绕z轴的旋转矩阵分别是:
PS:如果我们想更加通用一点,即点(x, y, z)绕轴(u, v, w)旋转θ的矩阵是什么?
如果u, v, w三者的平方和为1,即该向量是个单位向量,那么矩阵如下:
3. 缩放(scale)
对于一个三维坐标(x, y, z),我们想让它扩大2倍,则可以让它变成(2x, 2y, 2z)。写成矩阵乘法的话,V2 = M*V1,M如下图:
4. 统一变换
有没有什么方法让位移,旋转,缩放都成为统一的一种形式?
答:将三维坐标转换为四维坐标,然后使用线性变换。
线性变换(Linear Transformation / Xforms)是渲染和游戏引擎等图形学工具进行坐标变换的方式,是可逆的。
线性变换的等式如下:
V2 = M*V1
- V是齐次(homogeneous)四维向量(x,y,z,w),竖着写的
- M是齐次4×4矩阵
- 当w=1时,四维坐标会变成三维坐标
对于三维坐标(x, y, z),将其转换为四维坐标,可以直接加个1,即变成(x, y, z, 1)
对于四维坐标(x, y, z, w),都除以w即可转换为三维坐标,即(x/w, y/w, z/w)
1. 四维位移
这个图要从右向左看
从上图中可以看到,四维位移矩阵,是在一个四维单位矩阵(就是对角线都是1,其他都是0的矩阵)的最后一列,放入你想要位移的向量(tx, ty, tz)
2. 四维旋转
绕x轴转θ
从上图中可以看到,四维旋转矩阵,是在我们上面刚说的三维绕轴旋转矩阵的基础上,在最后一行和最后一列补上一个(0,0,0,1)。
3. 四维缩放
从右向左看
和旋转一个道理。
5. 四维变换的性质
-
可关联(associative)
你可以让一个坐标乘上一个旋转矩阵,再乘上一个位移矩阵,再乘上一个缩放矩阵,再乘上一个旋转矩阵……………… -
旋转和缩放矩阵可交换(communicative)
先旋转后缩放和先缩放后旋转的结果是一样的。RS = SR
位移不满足交换律
先位移再旋转和先旋转再位移结果是不一样的!因为旋转之后模型的正面朝向就变了,所以会向新的方向位移。
TS!=ST, TR!=RT -
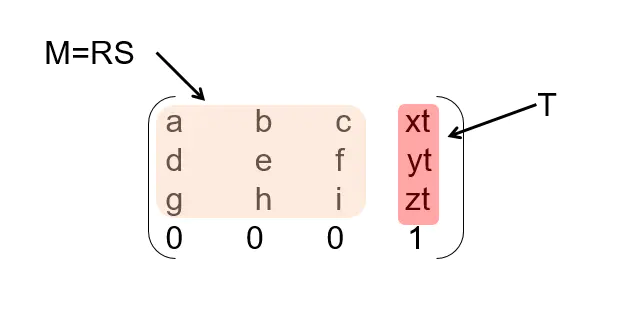
对于任何一个线性变换矩阵,我们可以把它拆解(decompose)为TRS或TSR三个矩阵的乘积的形式。
1)首先提取最后一列,得到位移
2)剩余的矩阵是R和S相乘的矩阵
我们可以先看一下S和R相乘的结果是什么样的SR相乘, 以Z轴旋转为例
从图中可以看出,SR矩阵,第一行的平方和开根就是Sx,第二行的平方和开根就是Sy,第三行的平方和开根就是Sz。第一行除以Sx,第二行除以Sy,第三行除以Sz,即可得到旋转矩阵。
6. 四维变换的逆变换
由于线性变换是可逆的,所以我们可以看一下位移旋转缩放的逆矩阵。
1. 位移
T的逆矩阵是-T,即向反方向移动。
2. 旋转
R的逆矩阵是R的转置矩阵,即以对角线翻转矩阵。
怎么理解呢?比如R是绕X轴旋转θ,那么逆操作就是绕X轴旋转-θ,带入-θ就会发现它变成了转置矩阵。
3. 缩放
S的逆矩阵是1/S,即把对角线上的三个元素都变成倒数,即反向缩放。
4. 线性变换Xforms
TSR的逆矩阵 = R的逆×S的逆×T的逆
以上转载自:https://www.jianshu.com/p/ac1b34420be7