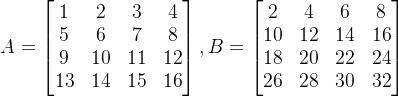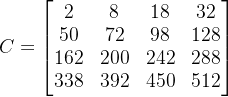yolov5x损失函数反向传播--chatgpt3.5指导

Yolov5x反向传播的路径，按顺序从检测头到主干网络列出：

1. YOLOv5检测头的反向传播：根据预测框和真实框之间的差异计算出损失函数值，然后通过反向传播来更新网络参数。

2. Path Aggregation Network（PAN）的反向传播：使用自适应加权路由策略对低层级特征进行修正，需要计算路由系数的梯度。

3. Feature Pyramid Network（FPN）的反向传播：由于FPN在自顶向下的特征传播过程中使用了上采样、下采样等操作，需要计算每层特征图的梯度。

4. Spatial Pyramid Pooling（SPP）模块的反向传播：在反向传播时需要计算其输出与前向传播的输入之间的梯度。

5. BottleneckCSP模块的反向传播：该模块包括了跳跃连接和残差连接，需要计算其输出与前向传播的输入之间的梯度。

6. Convolutional Block Layer (CBL)的反向传播：该层中使用卷积操作，需要计算其输出与前向传播的输入之间的梯度。

7. 输入特征图的反向传播：最终得到输入特征图的梯度，用于更新网络参数。

在YOLOv5x网络中，sigmoid和softmax函数是在训练阶段之前被用来生成预测输出的，而不是在反向传播的过程中。具体地说，Detection Head的输出会被应用一系列的sigmoid函数和softmax函数，将不同的预测输出投影到预定义的范围内，最终得到分类、定位和置信度预测。

在反向传播的过程中，我们需要计算损失函数关于网络各个参数的梯度，以便通过梯度下降来更新网络参数。而在反向传播过程中，我们只需要计算损失函数的导数，而不需要像预测阶段那样对输出结果进行sigmoid或者softmax变换。

因此，在上述分类损失项的反向传播中，我们只需要计算输出结果$\text{p}_i(c)$和标签值$\widehat{p}_i(c)$之间的导数即可，无需进行其他的变换。

YOLOv5的联合损失函数包括了3个部分：坐标损失函数、置信度损失函数和类别损失函数。

这是坐标损失

其中，表示预测框i 的坐标输出，表示真实框i 的坐标值， 表示系数。

好的，具体讲解反向传播的过程及公式。

接下来，我们来分别求关于第i个预测框的四个参数（）的偏导数。设表示对应的四个参数的偏导数：

本身不需要计算梯度，因为它是一个常数值（在训练过程中不会改变）。

在反向传播计算梯度时，我们需要计算每个损失项对应的梯度，然后根据链式法则求出整个网络的梯度。对于每个损失项，其梯度可以通过对它所涉及的参数进行求导获得。以为权重的中心点损失项来说，其梯度的计算可以简化为如下形式：

其中，为模型预测的目标边界框中心点坐标，为真实标注的目标边界框中心点坐标。在反向传播时，对于中心点损失项，我们需要计算上述两个梯度并传回给网络，用于调整中心点坐标的预测值，以优化整个网络的性能。

然后，我们可以根据链式法则逐层向前计算梯度信息，最终得到检测头的输出和输入之间的梯度信息，从而进行反向传播和权重更新。

假设我们需要对损失函数 L 进行反向传播，其中包含了坐标损失函数、LeakyReLU 激活函数卷积层（BN层，池化层不直接参与更新）在反向传播过程中，我们需要计算这些函数对其输入的导数，从而进行梯度的更新。

（1）坐标损失函数

对于坐标损失函数，以 $$ 为例，其对的导数为：

其中，表示第 l层的输出，是第l层卷积核的权重，是第 l层卷积层的偏置项， 表示 LeakyReLU 激活函数的导数，表示卷积运算，表示矩阵乘法。

2.分类损失函数：

在YOLOv5x的侦测头层反向传播过程中，要详写出分类损失项在每个函数中反向传播的运算过程，可以分为以下几步：

1. 的导数

对于和，它们的导数为：

其中，表示侦测头层输入的特征图，表示输入特征图的相应值。

2. 的导数

然后，对于，可以得到其对的导数为：

3. 反向传播至之前的卷积层中

将上述分类损失项在Detection Head中的反向传播计算得到的导数值，反向传播回之前的卷积层，以计算卷积核和偏置的偏导数。下面就是这个过程的具体数学计算过程：

1. 卷积核的偏导数

根据链式法则，可以将上述导数部分展开：

其中，表示输入到l-1层的第k个神经元的值。将这个式子代入上述卷积核偏导数的公式中，可以得到：

2. 偏置的偏导数

对于偏置的偏导数，可以计算得到如下公式：

可以看到，这个式子和卷积核偏导数的式子非常相似，唯一的区别是没有的因子，因为偏置不依赖于前一层的输入。

（2）LeakyReLU 激活函数

设损失函数 l 对 LeakyReLU 激活函数的输入 的导数为 ，则 LeakyReLU 函数的反向传播公式为：

其中，表示激活函数的输出， 表示元素级别的乘法。

为了更好地理解元素级别的乘法，我们可以通过一个具体的例子来说明。

假设有两个4x4的矩阵A和B，分别为：

则将A和B做元素级别的乘法得到的结果矩阵C为：

即。

同理，我们考虑两个向量和b=[5,6,7,8]做元素级别的乘法，则得到的结果向量，其中。

在深度学习中，元素级别的乘法常常用于特征之间的对应位置相乘，例如卷积层中的卷积核和输入特征图进行元素级别乘法的操作。

LeakyReLU 函数的导数具有比 ReLU 函数更为平缓的斜率，在反向传播时可以加速模型的收敛，避免梯度消失等问题。

（3）卷积层

设损失函数 L对卷积层的输出  的导数为 ，则卷积层的反向传播公式为：

其中，是第L层卷积核的权重，表示矩阵乘法。

这样，我们就得到了坐标损失函数、LeakyReLU 激活函数、和卷积层的反向传播公式，可以在实际应用中使用这些公式对神经网络的梯度进行计算和更新。

置信度损失函数：

其中，表示预测框 $i$ 的置信度输出，表示真实框i的置信度值，表示真实框i是否与预测框 i匹配，表示权重系数。

置信度损失函数的反向传播梯度  可以分为两部分：当 时，

当 时，

类别损失函数：

其中，表示预测框i属于类别 c 的概率，表示真实框 i 属于类别 c的概率，表示真实框 i 是否与预测框i 匹配。

类别损失函数的反向传播梯度 为：