Unity shader入门精要(学习总结)
(学习总结)
一,基础概念
什么是shader?
Unity Shader定义了渲染所需的各种代码(如顶点着色器和片元着色器)、属性(如使用哪些纹理等)和指令(渲染和标签设置等),而材质则允许我们调节这些属性,并将其最终赋给相应的模型。
着色器(英語:shader)是一种计算机程序,原本用于进行图像的浓淡处理(计算图像中的光照、亮度、颜色等),但近来,它也被用于完成很多不同领域的工作,比如处理CG特效、进行与浓淡处理无关的影片后期处理、甚至用于一些与计算机图形学无关的其它领域。
Shader结构,基础的shaderlab以及shader形式?
Unity Shader的基础结构
Shader “ShaderName”
{ Properties { // 属性
}
SubShader {
// 显卡A使用的子着色器
} SubShader {
// 显卡B使用的子着色器
} Fallback “VertexLit” }
Shader lab
所有的Unity Shader都是使用ShaderLab来编写的。
Shader 的形式
Shader “MyShader”
{
Properties { // 所需的各种属性
}
SubShader
{ // 真正意义上的Shader代码会出现在这里
// 表面着色器(Surface Shader)或者
// 顶点/片元着色器(Vertex/Fragment Shader)或者
// 固定函数着色器(Fixed Function Shader)
}
SubShader {
// 和上一个SubShader类似
}
}
基础渲染
CPU和GPU的通信
渲染流水线的起点是CPU,即应用阶段。应用阶段大致可分为下面3个阶段:
(1)把数据加载到显存中。
所有渲染所需的数据都需要从硬盘(Hard Disk Drive, HDD)中加载到系统内存(Random Access Memory, RAM)中。然后,网格和纹理等数据又被加载到显卡上的存储空间——显存(Video Random Access Memory, VRAM)中。这是因为,显卡对于显存的访问速度更快,而且大多数显卡对于RAM没有直接的访问权利。需要注意的是,真实渲染中需要加载到显存中的数据往往比较复杂许多。例如,顶点的位置信息、法线方向、顶点颜色、纹理坐标等。
当把数据加载到显存中后,RAM中的数据就可以移除了。但对于一些数据来说,CPU仍然需要访问它们(例如,我们希望CPU可以访问网格数据来进行碰撞检测),那么我们可能就不希望这些数据被移除,因为从硬盘加载到RAM的过程是十分耗时的。
在这之后,开发者还需要通过CPU来设置渲染状态,从而“指导”GPU如何进行渲染工作。
(2)设置渲染状态。
什么是渲染状态呢?一个通俗的解释就是,这些状态定义了场景中的网格是怎样被渲染的。例如,使用哪个顶点着色器(Vertex Shader)/片元着色器(Fragment Shader)、光源属性、材质等。如果我们没有更改渲染状态,那么所有的网格都将使用同一种渲染状态。图2.4显示了当使用同一种渲染状态时,渲染3个不同网格的结果。
在准备好上述所有工作后,CPU就需要调用一个渲染命令来告诉GPU:“嘿!老兄,我都帮你把数据准备好啦,你可以按照我的设置来开始渲染啦!”而这个渲染命令就是Draw Call。
(3)调用Draw Call(在本章的最后我们还会继续讨论它)。
相信接触过渲染优化的读者应该都听说过Draw Call。实际上,Draw Call就是一个命令,它的发起方是CPU,接收方是GPU。这个命令仅仅会指向一个需要被渲染的图元(primitives)列表,而不会再包含任何材质信息——这是因为我们已经在上一个阶段中完成了!图2.5形象化地阐释了这个过程。
当给定了一个Draw Call时,GPU就会根据渲染状态(例如材质、纹理、着色器等)和所有输入的顶点数据来进行计算,最终输出成屏幕上显示的那些漂亮的像素。而这个计算过程,就是我们下一节要讲的GPU流水线。
GPU的流水线
当GPU从CPU那里得到渲染命令后,就会进行一系列流水线操作,最终把图元渲染到屏幕上。
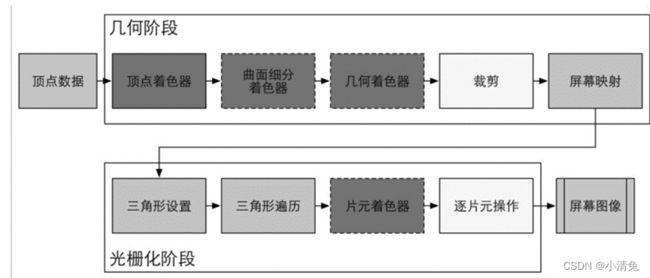 从图中可以看出,GPU的渲染流水线接收顶点数据作为输入。这些顶点数据是由应用阶段加载到显存中,再由Draw Call指定的。这些数据随后被传递给顶点着色器。
从图中可以看出,GPU的渲染流水线接收顶点数据作为输入。这些顶点数据是由应用阶段加载到显存中,再由Draw Call指定的。这些数据随后被传递给顶点着色器。
顶点着色器(Vertex Shader)是完全可编程的,它通常用于实现顶点的空间变换、顶点着色等功能。曲面细分着色器(Tessellation Shader)是一个可选的着色器,它用于细分图元。几何着色器(Geometry Shader)同样是一个可选的着色器,它可以被用于执行逐图元(Per-Primitive)的着色操作,或者被用于产生更多的图元。下一个流水线阶段是裁剪(Clipping),这一阶段的目的是将那些不在摄像机视野内的顶点裁剪掉,并剔除某些三角图元的面片。这个阶段是可配置的。例如,我们可以使用自定义的裁剪平面来配置裁剪区域,也可以通过指令控制裁剪三角图元的正面还是背面。几何概念阶段的最后一个流水线阶段是屏幕映射(Screen Mapping)。这一阶段是不可配置和编程的,它负责把每个图元的坐标转换到屏幕坐标系中。
从图中可以看出,GPU的渲染流水线接收顶点数据作为输入。这些顶点数据是由应用阶段加载到显存中,再由Draw Call指定的。这些数据随后被传递给顶点着色器。顶点着色器(Vertex Shader)是完全可编程的,它通常用于实现顶点的空间变换、顶点着色等功能。曲面细分着色器(Tessellation Shader)是一个可选的着色器,它用于细分图元。几何着色器(Geometry Shader)同样是一个可选的着色器,它可以被用于执行逐图元(Per-Primitive)的着色操作,或者被用于产生更多的图元。下一个流水线阶段是裁剪(Clipping),这一阶段的目的是将那些不在摄像机视野内的顶点裁剪掉,并剔除某些三角图元的面片。这个阶段是可配置的。例如,我们可以使用自定义的裁剪平面来配置裁剪区域,也可以通过指令控制裁剪三角图元的正面还是背面。几何概念阶段的最后一个流水线阶段是屏幕映射(Screen Mapping)。这一阶段是不可配置和编程的,它负责把每个图元的坐标转换到屏幕坐标系中。
1,顶点着色器(Vertex Shader)是流水线的第一个阶段,它的输入来自于CPU。顶点着色器的处理单位是顶点,也就是说,输入进来的每个顶点都会调用一次顶点着色器。顶点着色器本身不可以创建或者销毁任何顶点,而且无法得到顶点与顶点之间的关系。例如,我们无法得知两个顶点是否属于同一个三角网格。但正是因为这样的相互独立性,GPU可以利用本身的特性并行化处理每一个顶点,这意味着这一阶段的处理速度会很快。顶点着色器需要完成的工作主要有:坐标变换和逐顶点光照。当然,除了这两个主要任务外,顶点着色器还可以输出后续阶段所需的数据。图中展示了在顶点着色器中对顶点位置进行坐标变换并计算顶点颜色的过程。
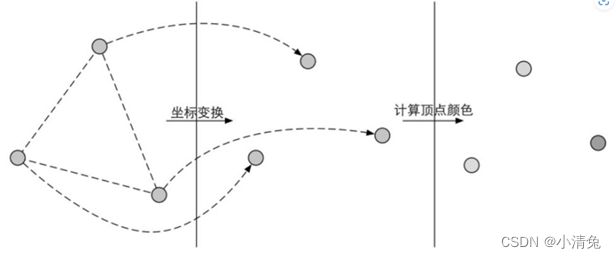
·坐标变换。顾名思义,就是对顶点的坐标(即位置)进行某种变换。顶点着色器可以在这一步中改变顶点的位置,这在顶点动画中是非常有用的。例如,我们可以通过改变顶点位置来模拟水面、布料等。但需要注意的是,无论我们在顶点着色器中怎样改变顶点的位置,一个最基本的顶点着色器必须完成的一个工作是,把顶点坐标从模型空间转换到齐次裁剪空间。想想看,我们在顶点着色器中是不是会看到类似下面的代码

类似上面这句代码的功能,就是把顶点坐标转换到齐次裁剪坐标系下,接着通常再由硬件做透视除法后,最终得到归一化的设备坐标(Normalized Device Coordinates , NDC)。。图展示了这样的一个转换过程。
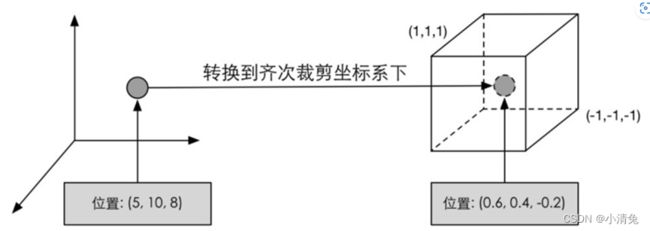 需要注意的是,图给出的坐标范围是OpenGL同时也是Unity使用的NDC,它的z分量范围在[-1, 1]之间,而在DirectX中,NDC的z分量范围是[0, 1]。顶点着色器可以有不同的输出方式。最常见的输出路径是经光栅化后交给片元着色器进行处理。
需要注意的是,图给出的坐标范围是OpenGL同时也是Unity使用的NDC,它的z分量范围在[-1, 1]之间,而在DirectX中,NDC的z分量范围是[0, 1]。顶点着色器可以有不同的输出方式。最常见的输出路径是经光栅化后交给片元着色器进行处理。
2,裁剪
由于我们的场景可能会很大,而摄像机的视野范围很有可能不会覆盖所有的场景物体,一个很自然的想法就是,那些不在摄像机视野范围的物体不需要被处理。而裁剪(Clipping)就是为了完成这个目的而被提出来的。一个图元和摄像机视野的关系有3种:完全在视野内、部分在视野内、完全在视野外。完全在视野内的图元就继续传递给下一个流水线阶段,完全在视野外的图元不会继续向下传递,因为它们不需要被渲染。而那些部分在视野内的图元需要进行一个处理,这就是裁剪。例如,一条线段的一个顶点在视野内,而另一个顶点不在视野内,那么在视野外部的顶点应该使用一个新的顶点来代替,这个新的顶点位于这条线段和视野边界的交点处。由于我们已知在NDC下的顶点位置,即顶点位置在一个立方体内,因此裁剪就变得很简单:只需要将图元裁剪到单位立方体内。图展示了这样的一个过程.
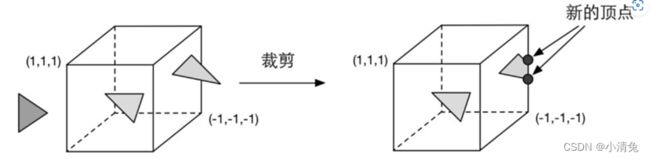 和顶点着色器不同,这一步是不可编程的,即我们无法通过编程来控制裁剪的过程,而是硬件上的固定操作,但我们可以自定义一个裁剪操作来对这一步进行配置。
和顶点着色器不同,这一步是不可编程的,即我们无法通过编程来控制裁剪的过程,而是硬件上的固定操作,但我们可以自定义一个裁剪操作来对这一步进行配置。
3,屏幕映射
这一步输入的坐标仍然是三维坐标系下的坐标(范围在单位立方体内)。屏幕映射(ScreenMapping)的任务是把每个图元的x和y坐标转换到屏幕坐标系(Screen Coordinates)下。屏幕坐标系是一个二维坐标系,它和我们用于显示画面的分辨率有很大关系。假设,我们需要把场景渲染到一个窗口上,窗口的范围是从最小的窗口坐标(x1,y1)到最大的窗口坐标(x2,y2),其中x1< x2且y1< y2。由于我们输入的坐标范围在-1到1,因此可以想象到,这个过程实际是一个缩放的过程,如图2.10所示。你可能会问,那么输入的z坐标会怎么样呢?屏幕映射不会对输入的z坐标做任何处理。实际上,屏幕坐标系和z坐标一起构成了一个坐标系,叫做窗口坐标系(Window Coordinates)。这些值会一起被传递到光栅化阶段。屏幕映射得到的屏幕坐标决定了这个顶点对应屏幕上哪个像素以及距离这个像素有多远。
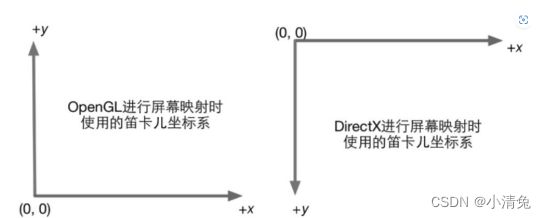
有一个需要引起注意的地方是,屏幕坐标系在OpenGL和DirectX之间的差异问题。OpenGL把屏幕的左下角当成最小的窗口坐标值,而DirectX则定义了屏幕的左上角为最小的窗口坐标值。图显示了这样的差异。
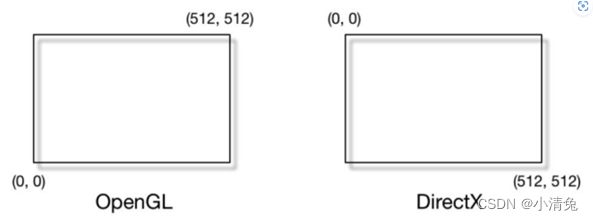
产生这种差异的原因是,微软的窗口都使用了这样的坐标系统,因为这和我们的阅读方式是一致的:从左到右、从上到下,并且很多图像文件也是按照这样的格式进行存储的。
不管原因如何,差异就这么造成了。留给我们开发者的就是,要时刻小心这样的差异,如果你发现得到的图像是倒转的,那么很有可能就是这个原因造成的。
4,三角形设置
由这一步开始就进入了光栅化阶段。从上一个阶段输出的信息是屏幕坐标系下的顶点位置以及和它们相关的额外信息,如深度值(z坐标)、法线方向、视角方向等。光栅化阶段有两个最重要的目标:计算每个图元覆盖了哪些像素,以及为这些像素计算它们的颜色。光栅化的第一个流水线阶段是三角形设置(Triangle Setup)。这个阶段会计算光栅化一个三角网格所需的信息。具体来说,上一个阶段输出的都是三角网格的顶点,即我们得到的是三角网格每条边的两个端点。但如果要得到整个三角网格对像素的覆盖情况,我们就必须计算每条边上的像素坐标。为了能够计算边界像素的坐标信息,我们就需要得到三角形边界的表示方式。这样一个计算三角网格表示数据的过程就叫做三角形设置。它的输出是为了给下一个阶段做准备。
5,三角形遍历
三角形遍历(Triangle Traversal)阶段将会检查每个像素是否被一个三角网格所覆盖。如果被覆盖的话,就会生成一个片元(fragment)。而这样一个找到哪些像素被三角网格覆盖的过程就是三角形遍历,这个阶段也被称为扫描变换(Scan Conversion)。三角形遍历阶段会根据上一个阶段的计算结果来判断一个三角网格覆盖了哪些像素,并使用三角网格3个顶点的顶点信息对整个覆盖区域的像素进行插值。图展示了三角形遍历阶段的简化计算过程。
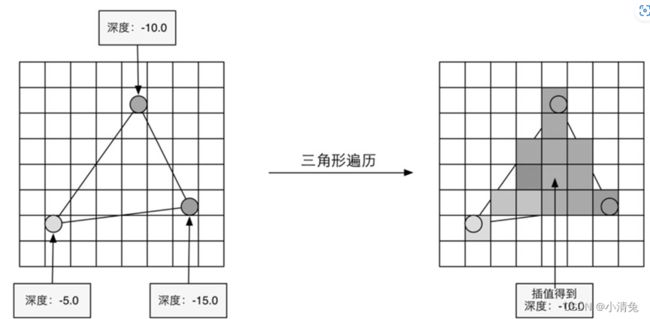
根据几何阶段输出的顶点信息,最终得到该三角网格覆盖的像素位置。对应像素会生成一个片元,而片元中的状态是对3个顶点的信息迚行插值得到的
这一步的输出就是得到一个片元序列。需要注意的是,一个片元并不是真正意义上的像素,而是包含了很多状态的集合,这些状态用于计算每个像素的最终颜色。这些状态包括了(但不限于)它的屏幕坐标、深度信息,以及其他从几何阶段输出的顶点信息,例如法线、纹理坐标等。
6,片元着色器
片元着色器(Fragment Shader)是另一个非常重要的可编程着色器阶段。在DirectX中,片元着色器被称为像素着色器(Pixel Shader),但片元着色器是一个更合适的名字,因为此时的片元并不是一个真正意义上的像素。前面的光栅化阶段实际上并不会影响屏幕上每个像素的颜色值,而是会产生一系列的数据信息,用来表述一个三角网格是怎样覆盖每个像素的。而每个片元就负责存储这样一系列数据。真正会对像素产生影响的阶段是下一个流水线阶段——逐片元操作(Per-Fragment Operations)。我们随后就会讲到。片元着色器的输入是上一个阶段对顶点信息插值得到的结果,更具体来说,是根据那些从顶点着色器中输出的数据插值得到的。而它的输出是一个或者多个颜色值。图显示了这样一个过程。
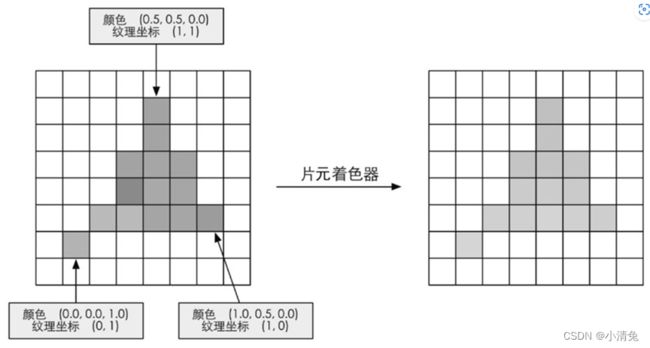 根据上一步插值后的片元信息,片元着色器计算该片元的输出颜色
根据上一步插值后的片元信息,片元着色器计算该片元的输出颜色
这一阶段可以完成很多重要的渲染技术,其中最重要的技术之一就是纹理采样。为了在片元着色器中进行纹理采样,我们通常会在顶点着色器阶段输出每个顶点对应的纹理坐标,然后经过光栅化阶段对三角网格的3个顶点对应的纹理坐标进行插值后,就可以得到其覆盖的片元的纹理坐标了。虽然片元着色器可以完成很多重要效果,但它的局限在于,它仅可以影响单个片元。也就是说,当执行片元着色器时,它不可以将自己的任何结果直接发送给它的邻居们。有一个情况例外,就是片元着色器可以访问到导数信息(gradient,或者说是derivative)。有兴趣的读者可以参考本章的扩展阅读部分。
7,逐片元操作
终于到了渲染流水线的最后一步。逐片元操作(Per-Fragment Operations)是OpenGL中的说法,在DirectX中,这一阶段被称为输出合并阶段(Output-Merger)。Merger这个词可能更容易让读者明白这一步骤的目的:合并。而OpenGL中的名字可以让读者明白这个阶段的操作单位,即是对每一个片元进行一些操作。那么问题来了,要合并哪些数据?又要进行哪些操作呢?
这一阶段有几个主要任务。
(1)决定每个片元的可见性。这涉及了很多测试工作,例如深度测试、模板测试等。(2)如果一个片元通过了所有的测试,就需要把这个片元的颜色值和已经存储在颜色缓冲区中的颜色进行合并,或者说是混合。需要指明的是,逐片元操作阶段是高度可配置性的,即我们可以设置每一步的操作细节。这在后面会讲到。这个阶段首先需要解决每个片元的可见性问题。这需要进行一系列测试。这就好比考试,一个片元只有通过了所有的考试,才能最终获得和GPU谈判的资格,这个资格指的是它可以和颜色缓冲区进行合并。如果它没有通过其中的某一个测试,那么对不起,之前为了产生这个片元所做的所有工作都是白费的,因为这个片元会被舍弃掉。Poor fragment!图给出了简化后的逐片元操作所做的操作。

逐片元操作阶段所做的操作。只有通过了所有的测试后,新生成的片元才能和颜色缓冲区中已经存在的像素颜色迚行混合,最后再写入颜色缓冲区中
测试的过程实际上是个比较复杂的过程,而且不同的图形接口(例如OpenGL和DirectX)的实现细节也不尽相同。这里给出两个最基本的测试——深度测试和模板测试的实现过程。能否理解这些测试过程将关乎读者是否可以理解本书后面章节中提到的渲染队列,尤其是处理透明效果时出现的问题。图给出了深度测试和模板测试的简化流程图。
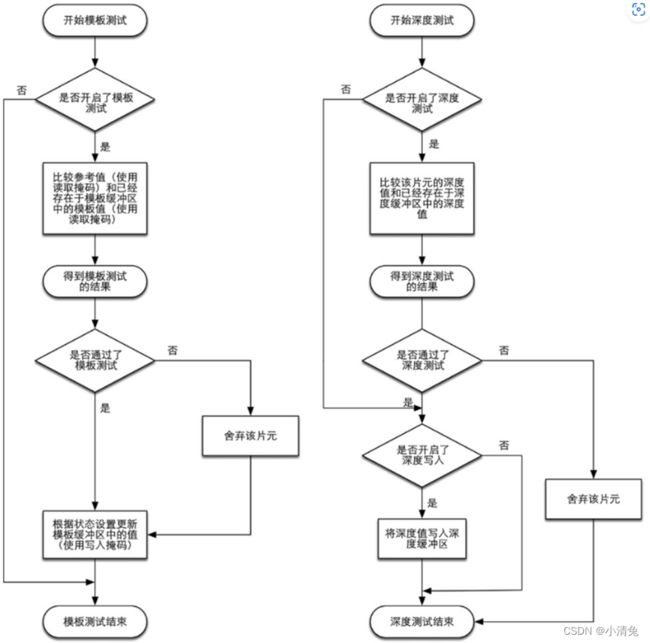
模板测试和深度测试的简化流程图
我们先来看模板测试(Stencil Test)。与之相关的是模板缓冲(Stencil Buffer)。实际上,模板缓冲和我们经常听到的颜色缓冲、深度缓冲几乎是一类东西。如果开启了模板测试,GPU会首先读取(使用读取掩码)模板缓冲区中该片元位置的模板值,然后将该值和读取(使用读取掩码)到的参考值(reference value)进行比较,这个比较函数可以是由开发者指定的,例如小于时舍弃该片元,或者大于等于时舍弃该片元。如果这个片元没有通过这个测试,该片元就会被舍弃。不管一个片元有没有通过模板测试,我们都可以根据模板测试和下面的深度测试结果来修改模板缓冲区,这个修改操作也是由开发者指定的。开发者可以设置不同结果下的修改操作,例如,在失败时模板缓冲区保持不变,通过时将模板缓冲区中对应位置的值加1等。模板测试通常用于限制渲染的区域。另外,模板测试还有一些更高级的用法,如渲染阴影、轮廓渲染等
如果一个片元幸运地通过了模板测试,那么它会进行下一个测试——深度测试(Depth Test)。相信很多读者都听到过这个测试。这个测试同样是可以高度配置的。如果开启了深度测试,GPU会把该片元的深度值和已经存在于深度缓冲区中的深度值进行比较。这个比较函数也是可由开发者设置的,例如小于时舍弃该片元,或者大于等于时舍弃该片元。通常这个比较函数是小于等于的关系,即如果这个片元的深度值大于等于当前深度缓冲区中的值,那么就会舍弃它。这是因为,我们总想只显示出离摄像机最近的物体,而那些被其他物体遮挡的就不需要出现在屏幕上。如果这个片元没有通过这个测试,该片元就会被舍弃。和模板测试有些不同的是,如果一个片元没有通过深度测试,它就没有权利更改深度缓冲区中的值。而如果它通过了测试,开发者还可以指定是否要用这个片元的深度值覆盖掉原有的深度值,这是通过开启/关闭深度写入来做到的。我们在后面的学习中会发现,透明效果和深度测试以及深度写入的关系非常密切。
为什么需要合并?我们要知道,这里所讨论的渲染过程是一个物体接着一个物体画到屏幕上的。而每个像素的颜色信息被存储在一个名为颜色缓冲的地方。因此,当我们执行这次渲染时,颜色缓冲中往往已经有了上次渲染之后的颜色结果,那么,我们是使用这次渲染得到的颜色完全覆盖掉之前的结果,还是进行其他处理?这就是合并需要解决的问题。对于不透明物体,开发者可以关闭混合(Blend)操作。这样片元着色器计算得到的颜色值就会直接覆盖掉颜色缓冲区中的像素值。但对于半透明物体,我们就需要使用混合操作来让这个物体看起来是透明的。图展示了一个简化版的混合操作的流程图。
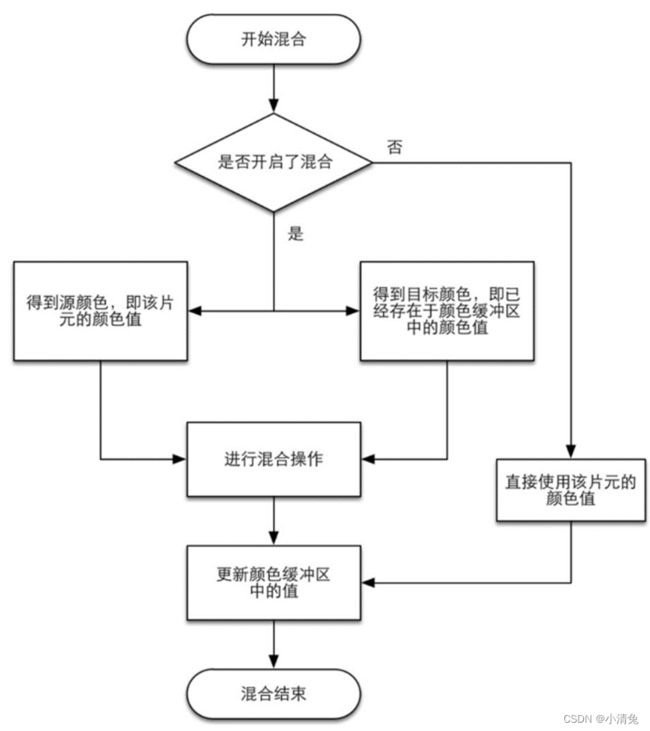
混合操作的简化流程图
从流程图中我们可以发现,混合操作也是可以高度配置的:开发者可以选择开启/关闭混合功能。如果没有开启混合功能,就会直接使用片元的颜色覆盖掉颜色缓冲区中的颜色,而这也是很多初学者发现无法得到透明效果的原因(没有开启混合功能)。如果开启了混合,GPU会取出源颜色和目标颜色,将两种颜色进行混合。源颜色指的是片元着色器得到的颜色值,而目标颜色则是已经存在于颜色缓冲区中的颜色值。之后,就会使用一个混合函数来进行混合操作。这个混合函数通常和透明通道息息相关,例如根据透明通道的值进行相加、相减、相乘等。混合很像Photoshop中对图层的操作:每一层图层可以选择混合模式,混合模式决定了该图层和下层图层的混合结果,而我们看到的图片就是混合后的图片。
上面给出的测试顺序并不是唯一的,而且虽然从逻辑上来说这些测试是在片元着色器之后进行的,但对于大多数GPU来说,它们会尽可能在执行片元着色器之前就进行这些测试。这是可以理解的,想象一下,当GPU在片元着色器阶段花了很大力气终于计算出片元的颜色后,却发现这个片元根本没有通过这些检验,也就是说这个片元还是被舍弃了,那之前花费的计算成本全都浪费了!图2.17给出了这样一个场景。
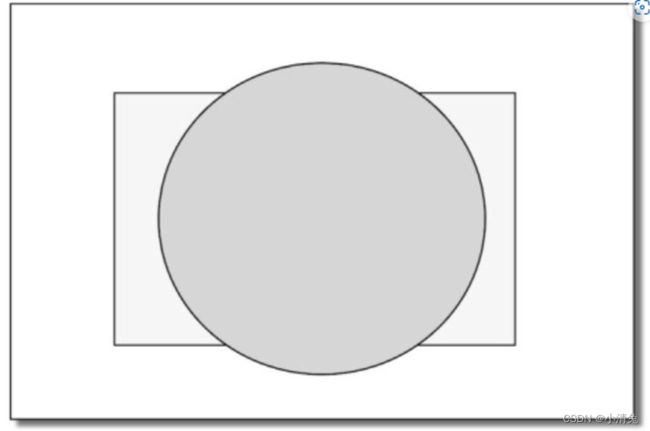
场景中包含了两个对象:球和长方体,绘制顺序是先绘制球(在屏幕上显示为圆),再绘制长方体(在屏幕上显示为长方形)。如果深度测试在片元着色器之后执行,那么在渲染长方体时,虽然它的大部分区域都被遮挡在球的后面,即它所覆盖的绝大部分片元根本无法通过深度测试,但是我们仍然需要对这些片元执行片元着色器,造成了很大的性能浪费
作为一个想充分提高性能的GPU,它会希望尽可能早地知道哪些片元是会被舍弃的,对于这些片元就不需要再使用片元着色器来计算它们的颜色。在Unity给出的渲染流水线中,我们也可以发现它给出的深度测试是在片元着色器之前。这种将深度测试提前执行的技术通常也被称为Early-Z技术。希望读者看到这里时不会因此感到困惑
但是,如果将这些测试提前的话,其检验结果可能会与片元着色器中的一些操作冲突。例如,如果我们在片元着色器进行了透明度测试,而这个片元没有通过透明度测试,我们会在着色器中调用API(例如clip函数)来手动将其舍弃掉。这就导致GPU无法提前执行各种测试。因此,现代的GPU会判断片元着色器中的操作是否和提前测试发生冲突,如果有冲突,就会禁用提前测试。但是,这样也会造成性能上的下降,因为有更多片元需要被处理了。这也是透明度测试会导致性能下降的原因。
当模型的图元经过了上面层层计算和测试后,就会显示到我们的屏幕上。我们的屏幕显示的就是颜色缓冲区中的颜色值。但是,为了避免我们看到那些正在进行光栅化的图元,GPU会使用双重缓冲(Double Buffering)的策略。这意味着,对场景的渲染是在幕后发生的,即在后置缓冲(Back Buffer)中。一旦场景已经被渲染到了后置缓冲中,GPU就会交换后置缓冲区和前置缓冲(Front Buffer)中的内容,而前置缓冲区是之前显示在屏幕上的图像。由此,保证了我们看到的图像总是连续的
总结如下:
虽然我们上面讲了很多,但其真正的实现过程远比上面讲到的要复杂。需要注意的是,读者可能会发现这里给出的流水线名称、顺序可能和在一些资料上看到的不同。一个原因是由于图像编程接口(如OpenGL和DirectX)的实现不尽相同,另一个原因是GPU在底层可能做了很多优化,例如上面提到的会在片元着色器之前就进行深度测试,似避免无谓的计算。虽然渲染流水线比较复杂,但Unity作为一个非常出色的平台为我们封装了很多功能。更多时候,我们只需要在一个Unity Shader设置一些输入、编写顶点着色器和片元着色器、设置一些状态就可以达到大部分常见的屏幕效果。这是Unity吸引人的魅力之处,但这样的缺点在于,封装性会导致编程自由度下降,使很多初学者迷失方向,无法掌握其背后的原理,并在出现问题时,往往无法找到错误原因,这是在学习Unity Shader时普遍的遭遇。渲染流水线几乎和本书所有章节都息息相关,如果读者此时仍然无法完全理解渲染流水线,仍可以继续学习下去。但如果读者在学习过程中发现有些设置或代码无法理解,可以不断查阅本章内容,相信会有更深的理解。
Unity的基础光照
自发光(emissive)部分使用cmissive来表示。
这个部分用于描述当给定一个方向时,一个表面本身会向该方向发射多少辐射量。需要注意的是,如果没有使用全局光照(global illumination)技术,这些自发光的表面并不会真的照亮周围的物体,而是它本身看起来更亮了而已。
光线也可以直接由光源发射进入摄像机,而不需要经过任何物体的反射。标准光照模型使用自发光来计算这个部分的贡献度。它的计算也很简单,就是直接使用了该材质的自发光颜色:cemissive=memissive通常在实时渲染中,自发光的表面往往并不会照亮周围的表面,也就是说,这个物体并不会被当成一个光源。
·高光反射(specular)部分,使用cspecular来表示。这个部分用于描述当光线从光源照射到模型表面时,该表面会在完全镜面反射方向散射多少辐射量。
这里的高光反射是一种经验模型,也就是说,它并不完全符合真实世界中的高光反射现象。它可用于计算那些沿着完全镜面反射方向被反射的光线,这可以让物体看起来是有光泽的,例如金属材质。
计算高光反射需要知道的信息比较多,如表面法线、视角方向、光源方向、反射方向等
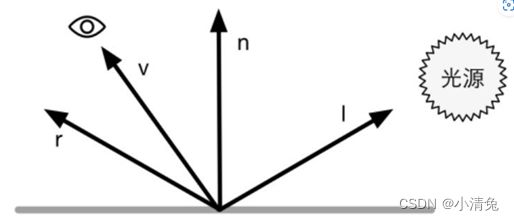
使用Phong模型计算高光反射
在这四个矢量中,我们实际上只需要知道其中3个矢量即可,而第四个矢量——反射方向可以通过其他信息计算得到
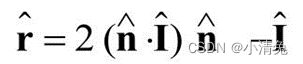 这样,我们就可以利用Phong模型来计算高光反射的部分:
这样,我们就可以利用Phong模型来计算高光反射的部分: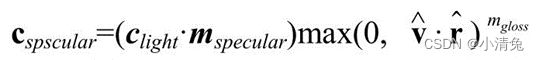
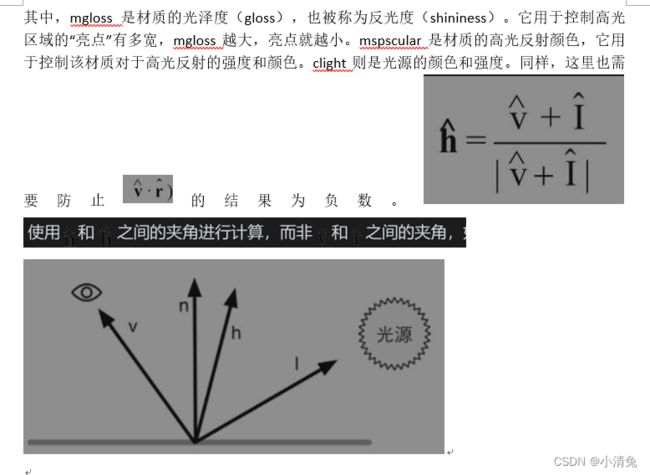
Blinn模型的公式如下:
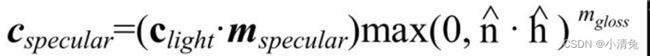 在硬件实现时,如果摄像机和光源距离模型足够远的话,Blinn模型会快于Phong模型,这是因为,此时可以认为[插图]和[插图]都是定值,因此[插图]将是一个常量。但是,当[插图]或者[插图]不是定值时,Phong模型可能反而更快一些。需要注意的是,这两种光照模型都是经验模型,也就是说,我们不应该认为Blinn模型是对“正确的”Phong模型的近似。实际上,在一些情况下,Blinn模型更符合实验结果。
在硬件实现时,如果摄像机和光源距离模型足够远的话,Blinn模型会快于Phong模型,这是因为,此时可以认为[插图]和[插图]都是定值,因此[插图]将是一个常量。但是,当[插图]或者[插图]不是定值时,Phong模型可能反而更快一些。需要注意的是,这两种光照模型都是经验模型,也就是说,我们不应该认为Blinn模型是对“正确的”Phong模型的近似。实际上,在一些情况下,Blinn模型更符合实验结果。
·漫反射(diffuse)部分,使用cdiffuse来表示。这个部分用于描述,当光线从光源照射到模型表面时,该表面会向每个方向散射多少辐射量。
漫反射光照是用于对那些被物体表面随机散射到各个方向的辐射度进行建模的。在漫反射中,视角的位置是不重要的,因为反射是完全随机的,因此可以认为在任何反射方向上的分布都是一样的。但是,入射光线的角度很重要。漫反射光照符合兰伯特定律(Lambert’s law):反射光线的强度与表面法线和光源方向之间夹角的余弦值成正比。因此,漫反射部分的计算如下:
![]()
![]() 是表面法线
是表面法线
![]() 是指向光源的单位矢量,mdiffuse是材质的漫反射颜色,clight是光源颜色。需要注意的是,我们需要防止法线和光源方向点乘的结果为负值,为此,我们使用取最大值的函数来将其截取到0,这可以防止物体被从后面来的光源照亮。
是指向光源的单位矢量,mdiffuse是材质的漫反射颜色,clight是光源颜色。需要注意的是,我们需要防止法线和光源方向点乘的结果为负值,为此,我们使用取最大值的函数来将其截取到0,这可以防止物体被从后面来的光源照亮。
·环境光(ambient)部分,使用cambient来表示。它用于描述其他所有的间接光照。
虽然标准光照模型的重点在于描述直接光照,但在真实的世界中,物体也可以被间接光照(indirect light)所照亮。间接光照指的是,光线通常会在多个物体之间反射,最后进入摄像机,也就是说,在光线进入摄像机之前,经过了不止一次的物体反射。例如,在红地毯上放置一个浅灰色的沙发,那么沙发底部也会有红色,这些红色是由红地毯反射了一部分光线,再反弹到沙发上的。在标准光照模型中,我们使用了一种被称为环境光的部分来近似模拟间接光照。环境光的计算非常简单,它通常是一个全局变量,即场景中的所有物体都使用这个环境光。计算环境光的部分:cambient=gambient
逐像素还是逐顶点
我们给出了基本光照模型使用的数学公式,那么我们在哪里计算这些光照模型呢?通常来讲,我们有两种选择:在片元着色器中计算,也被称为逐像素光照(per-pixel lighting);在顶点着色器中计算,也被称为逐顶点光照(per-vertex lighting)。在逐像素光照中,我们会以每个像素为基础,得到它的法线(可以是对顶点法线插值得到的,也可以是从法线纹理中采样得到的),然后进行光照模型的计算。这种在面片之间对顶点法线进行插值的技术被称为Phong着色(Phong shading),也被称为Phong插值或法线插值着色技术。这不同于我们之前讲到的Phong光照模型。
与之相对的是逐顶点光照,也被称为高洛德着色(Gouraud shading)。在逐顶点光照中,我们在每个顶点上计算光照,然后会在渲染图元内部进行线性插值,最后输出成像素颜色。由于顶点数目往往远小于像素数目,因此逐顶点光照的计算量往往要小于逐像素光照。但是,由于逐顶点光照依赖于线性插值来得到像素光照,因此,当光照模型中有非线性的计算(例如计算高光反射时)时,逐顶点光照就会出问题。在后面的章节中,我们将会看到这种情况。而且,由于逐顶点光照会在渲染图元内部对顶点颜色进行插值,这会导致渲染图元内部的颜色总是暗于顶点处的最高颜色值,这在某些情况下会产生明显的棱角现象。
总结:
虽然标准光照模型仅仅是一个经验模型,也就是说,它并不完全符合真实世界中的光照现象。但由于它的易用性、计算速度和得到的效果都比较好,因此仍然被广泛使用。而也是由于它的广泛使用性,这种标准光照模型有很多不同的叫法。例如,一些资料中称它为Phong光照模型,因为裴祥风(Bui Tuong Phong)首先提出了使用漫反射和高光反射的和来对反射光照进行建模的基本思想,并且提出了基于经验的计算高光反射的方法(用于计算漫反射光照的兰伯特模型在那时已经被提出了)。而后,由于Blinn的方法简化了计算而且在某些情况下计算更快,我们把这种模型称为Blinn-Phong光照模型。但这种模型有很多局限性。首先,有很多重要的物理现象无法用Blinn-Phong模型表现出来,例如菲涅耳反射(Fresnel reflection)。其次,Blinn-Phong模型是各项同性(isotropic)的,也就是说,当我们固定视角和光源方向旋转这个表面时,反射不会发生任何改变。但有些表面是具有各向异性(anisotropic)反射性质的,例如拉丝金属、毛发等
漫反射和高光反射的光照模型
基础纹理(单张,凹凸,渐变,遮罩)
透明效果(透明度测试,透明度混合,半透明,双面透贴不透贴)
Unity的标准shader
高级纹理(立方体纹理,渲染纹理,程度纹理,(纹理动画,顶点动画),屏幕后处理(屏幕亮度饱和度对比度,边缘检测,高斯模糊,Bloom效果,运动模糊))
深度和法线纹理(获取深度和法线纹理,运动模糊2,边缘检测2,全局雾效)
非真实感渲染(卡通,素描)
使用噪声(消融,水波,全局雾效2)
注意:代码部分
自行查看
链接:https://pan.baidu.com/s/1YEWZHW-21nKPBIIX2q8-1w?pwd=g7nd
提取码:g7nd
Unity shader的基础数学
1,笛卡尔坐标系
我们使用数学绝大部分都是为了计算位置、距离和角度等变量。这些计算大部分都是在笛卡儿坐标系下进行的。
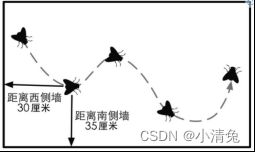
卡儿坐标系来源于笛卡儿对天花板上一只苍蝇的运动轨迹的观察。笛卡儿发现,可以使用苍蝇距不同墙面的距离来描述它的当前位置
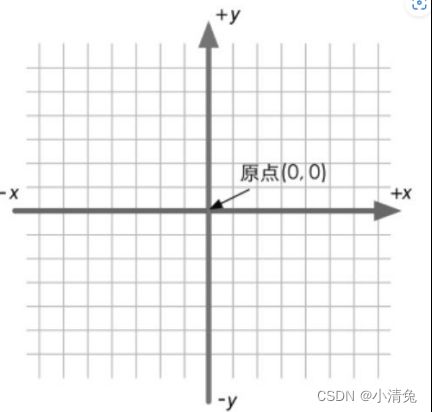
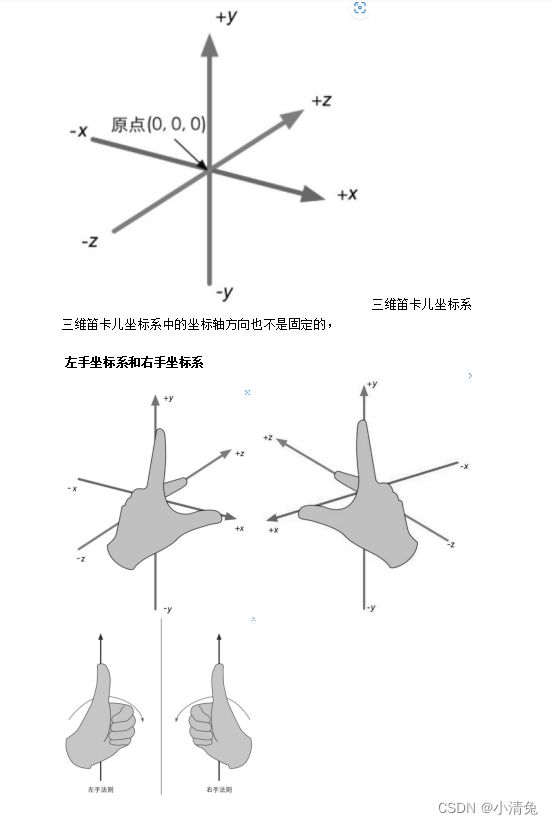
二维笛卡儿坐标系
一个二维的笛卡儿坐标系包含了两个部分的信息:
·一个特殊的位置,即原点,它是整个坐标系的中心。
·两条过原点的互相垂直的矢量,即x轴和y轴。这些坐标轴也被称为是该坐标系的基矢
2,点和矢量
点(point)是n维空间(游戏中主要使用二维和三维空间)中的一个位置,它没有大小、宽度这类概念。在笛卡儿坐标系中,我们可以使用2个或3个实数来表示一个点的坐标,如P=(Px, Py)表示二维空间的点,P=(Px, Py,Pz)表示三维空间中的点。
矢量(vector,也被称为向量)的定义则复杂一些。在数学家看来,矢量就是一串数字。你可能要问了,点的表达式不也是一串数字吗?没错,但矢量存在的意义更多是为了和标量(scalar)区分开来。通常来讲,矢量是指n维空间中一种包含了模(magnitude)和方向(direction)的有向线段,我们通常讲到的速度(velocity)就是一种典型的矢量。例如,这辆车的速度是向南80km/h(向南指明了矢量的方向,80km/h指明了矢量的模)。而标量只有模没有方向,生活中常常说到的距离(distance)就是一种标量。例如,我家离学校只有200m(200m就是一个标量)。
具体来讲。
·矢量的模指的是这个矢量的长度。一个矢量的长度可以是任意的非负数。
·矢量的方向则描述了这个矢量在空间中的指向。矢量的表示方法和点类似。我们可以使用v=(x, y)来表示二维矢量,用v=(x, y, z)来表示三维矢量,用v=(x, y, z, w)来表示四维矢量。为了方便阐述,我们对不同类型的变量在书写和印刷上使用不同的样式。
·对于标量,我们使用小写字母来表示,如a, b, x, y, z, θ, α等。
·对于矢量,我们使用小写的粗体字母来表示,如a, b, u, v等。
·对于后面要学习的矩阵,我们使用大写的粗体字母来表示,如A, B, S, M, R等。
一个矢量通常由一个箭头来表示。我们有时会讲到一个矢量的头(head)和尾(tail)。矢量的头指的是它的箭头所在的端点处,而尾指的是另一个端点处
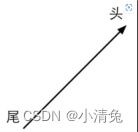 从矢量的定义来看,它只有模和方向两个属性,并没有位置信息。这听起来很难理解,但实际上在生活中我们总是会和这样的矢量打交道。例如,当我们讲到一个物体的速度时,可能会这样说“那个小偷正在以100km/h的速度向南逃窜”(快抓住他!),这里的“以100km/h的速度向南”就可以使用一个矢量来表示。通常,矢量被用于表示相对于某个点的偏移(displacement),也就是说它是一个相对量。只要矢量的模和方向保持不变,无论放在哪里,都是同一个矢量。
从矢量的定义来看,它只有模和方向两个属性,并没有位置信息。这听起来很难理解,但实际上在生活中我们总是会和这样的矢量打交道。例如,当我们讲到一个物体的速度时,可能会这样说“那个小偷正在以100km/h的速度向南逃窜”(快抓住他!),这里的“以100km/h的速度向南”就可以使用一个矢量来表示。通常,矢量被用于表示相对于某个点的偏移(displacement),也就是说它是一个相对量。只要矢量的模和方向保持不变,无论放在哪里,都是同一个矢量。
点和矢量的区别
点是一个没有大小之分的空间中的位置,而矢量是一个有模和方向但没有位置的量。从这里看,点和矢量具有不同的意义。但是,从表示方式上两者非常相似。
矢量和标量的乘法/除法
一个矢量也可以被一个非零的标量除。这等同于和这个标量的倒数相乘:

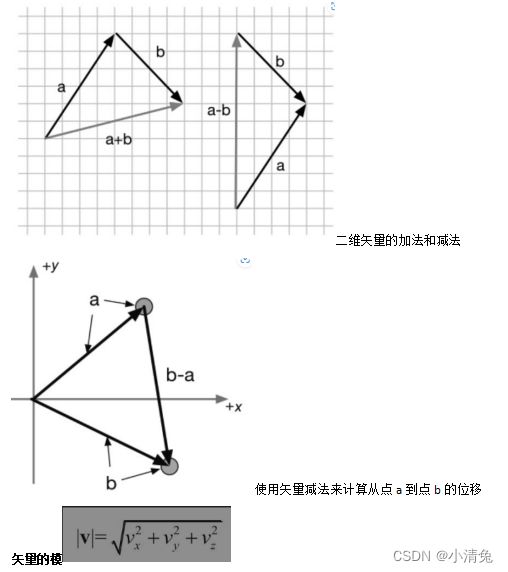
从几何意义上来看,对于加法,我们可以把矢量a的头连接到矢量b的尾,然后画一条从a的尾到b的头的矢量,来得到a和b相加后的矢量。也就是说,如果我们从一个起点开始进行了一个位置偏移a,然后又进行一个位置偏移b,那么就等同于进行了一个a+b的位置偏移。这被称为矢量加法的三角形定则(triangle rule)。矢量的减法是类似的
单位矢量
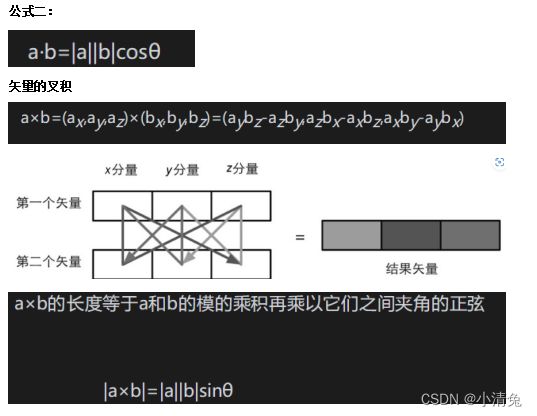
矢量的点积
![]()
点积具有一些很重要的性质,在Shader的计算中,我们会经常利用这些性质来帮助计算
性质一:点积可结合标量乘法。上面的“结合”是说,点积的操作数之一可以是另一个运算的结果,即矢量和标量相乘的结果。公式如下:(ka)·b= a·(kb)=k(a·b)也就是说,对点积中其中一个矢量进行缩放的结果,相当于对最后的点积结果进行缩放。
性质二:点积可结合矢量加法和减法,和性质一类似。这里的“结合”指的是,点积的操作数可以是矢量相加或相减后的结果。用公式表达就是:a·(b+ c)= a·b+ a·c
性质三:一个矢量和本身进行点积的结果,是该矢量的模的平方。这点可以很容易从公式验证得到:v ·v=vxvx+vyvy+vzvz=|v|2
这意味着,我们可以直接利用点积来求矢量的模,而不需要使用模的计算公式。当然,我们需要对点积结果进行开平方的操作来得到真正的模。但很多情况下,我们只是想要比较两个矢量的长度大小,因此可以直接使用点积的结果。毕竟,开平方的运算需要消耗一定性能。现在是时候来看点积的另一种表示方法了。这种方法是从三角代数的角度出发的,这种表示方法更加具有几何意义,因为它可以明确地强调出两个矢量之间的角度。
3,矩阵

矩阵和矩阵的乘法
如果两个矩阵的行列不满足上面的规定怎么办?那么很抱歉,这两个矩阵就不能相乘,因为它们之间的乘法是没有被定义的(当然,读者完全可以自己定义一种新的乘法,但是数学家们会不会买账就不一定了)。那么为什么会有上面的规定呢?等我们理解了矩阵乘法的操作过程自然就会明白。我们先给出看起来很复杂难懂(当给出直观的表式后读者会发现其实它没那么难懂)的数学表达式:设有r×n的矩阵A和一个n×c的矩阵B,它们相乘会得到一个r×c的矩阵C=AB。那么,C中的每一个元素cij等于A的第i行所对应的矢

4,矩阵的几何意义,(变换)
什么是变换
变换(transform),指的是我们把一些数据,如点、方向矢量甚至是颜色等,通过某种方式进行转换的过程。在计算机图形学领域,变换非常重要。尽管通过变换我们能够进行的操作是有限的,但这些操作已经足够奠定变换在图形学领域举足轻重的地位了。
我们先来看一个非常常见的变换类型——线性变换(linear transform)。线性变换指的是那些可以保留矢量加和标量乘的变换。用数学公式来表示这两个条件就是:
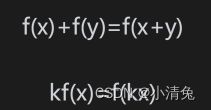
可见,两个运算得到的结果是不一样的。因此,我们不能用一个3×3的矩阵来表示一个平移变换。这是我们不希望看到的,毕竟平移变换是非常常见的一种变换。这样,就有了仿射变换(affine transform)。仿射变换就是合并线性变换和平移变换的变换类型。仿射变换可以使用一个4×4的矩阵来表示,为此,我们需要把矢量扩展到四维空间下,这就是齐次坐标空间(homogeneous space)。
齐次坐标
齐次坐标是一个四维矢量。那么,我们如何把三维矢量转换成齐次坐标呢?对于一个点,从三维坐标转换成齐次坐标是把其w分量设为1,而对于方向矢量来说,需要把其w分量设为0。这样的设置会导致,当用一个4×4矩阵对一个点进行变换时,平移、旋转、缩放都会施加于该点。但是如果是用于变换一个方向矢量,平移的效果就会被忽略。我们可以从下面的内容中理解这些差异的原因
分解基础变换矩阵
们已经知道,可以使用一个4×4的矩阵来表示平移、旋转和缩放。我们把表示纯平移、纯旋转和纯缩放的变换矩阵叫做基础变换矩阵。这些矩阵具有一些共同点,
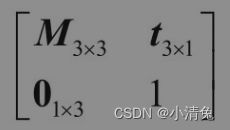
其中,左上角的矩阵M3×3用于表示旋转和缩放,t3×1用于表示平移,01×3是零矩阵,即01×3=[0 0 0],右下角的元素就是标量1。
平移矩阵
平移变换不会对方向矢量产生任何影响。这点很容易理解,我们在学习矢量的时候就说过了,矢量没有位置属性,也就是说它可以位于空间中的任意一点,因此对位置的改变(即平移)不应该对四维矢量产生影响。
缩放矩阵
如果缩放系数kx=ky=kz,我们把这样的缩放称为统一缩放(uniform scale),否则称为非统一缩放(nonuniform scale)。从外观上看,统一缩放是扩大整个模型,而非统一缩放会拉伸或挤压模型。更重要的是,统一缩放不会改变角度和比例信息,而非统一缩放会改变与模型相关的角度和比例。例如在对法线进行变换时,如果存在非统一缩放,直接使用用于变换顶点的变换矩阵的话,就会得到错误的结果。
如果我们希望在任意方向上进行缩放,就需要使用一个复合变换。其中一种方法的主要思想就是,先将缩放轴变换成标准坐标轴,然后进行沿坐标轴的缩放,再使用逆变换得到原来的缩放轴朝向。
旋转矩阵
旋转矩阵的逆矩阵是旋转相反角度得到的变换矩阵。旋转矩阵是正交矩阵,而且多个旋转矩阵之间的串联同样是正交的。
复合变换
我们可以把平移、旋转和缩放组合起来,来形成一个复杂的变换过程。例如,可以对一个模型先进行大小为(2, 2, 2)的缩放,再绕y轴旋转30°,最后向z轴平移4个单位。复合变换可以通过矩阵的串联来实现。上面的变换过程可以使用下面的公式来计算:
pnew=MtranslationMrotationMscalθ oldp
由于上面我们使用的是列矩阵,因此阅读顺序是从右到左,即先进行缩放变换,再进行旋转变换,最后进行平移变换。需要注意的是,变换的结果是依赖于变换顺序的,由于矩阵乘法不满足交换律,因此矩阵的乘法顺序很重要。也就是说,不同的变换顺序得到的结果可能是一样的。想象一下,如果让读者向前一步然后左转,记住此时的位置。然后回到原位,这次先左转再向前走一步,得到的位置和上一次是不一样的。究其本质,是因为矩阵的乘法不满足交换律,因此不同的乘法顺序得到的结果是不一样的。
在绝大多数情况下,我们约定变换的顺序就是先缩放,再旋转,最后平移‘
’
5,坐标空间
坐标空间的变换
我们先要为后面的内容做些数学铺垫。在渲染流水线中,我们往往需要把一个点或方向矢量从一个坐标空间转换到另一个坐标空间。这个过程到底是怎么实现的呢?我们把问题一般化。我们知道,要想定义一个坐标空间,必须指明其原点位置和3个坐标轴的方向。而这些数值实际上是相对于另一个坐标空间的(读者需要记住,所有的都是相对的)。也就是说,坐标空间会形成一个层次结构——每个坐标空间都是另一个坐标空间的子空间,反过来说,每个空间都有一个父(parent)坐标空间。对坐标空间的变换实际上就是在父空间和子空间之间对点和矢量进行变换。假设,现在有父坐标空间P以及一个子坐标空间C。我们知道在父坐标空间中子坐标空间的原点位置以及3个单位坐标轴。我们一般会有两种需求:一种需求是把子坐标空间下表示的点或矢量Ac转换到父坐标空间下的表示Ap,另一个需求是反过来,即把父坐标空间下表示的点或矢量Bp转换到子坐标空间下的表示Bc。我们可以使用下面的公式来表示这两种需求:

其中,Mc→p表示的是从子坐标空间变换到父坐标空间的变换矩阵,而Mp→c是其逆矩阵(即反向变换)。那么,现在的问题就是,如果求解这些变换矩阵?事实上,我们只需要解出两者之一即可,另一个矩阵可以通过求逆矩阵的方式来得到。下面,我们就来讲解如何求出从子坐标空间到父坐标空间的变换矩阵Mc→p。首先,我们来回顾一个看似很简单的问题:当给定一个坐标空间以及其中一点(a,b, c)时,我们是如何知道该点的位置的呢?
我们可以通过4个步骤来确定它的位置:
(1)从坐标空间的原点开始;
(2)向x轴方向移动a个单位。
(3)向y轴方向移动b个单位
(4)向z轴方向移动c个单位。
需要说明的是,上面的步骤只是我们的想象,这个点实际上并没有发生移动。上面的步骤看起来再简单不过了,坐标空间的变换就蕴含在上面的4个步骤中。现在,我们已知子坐标空间C的3个坐标轴在父坐标空间P下的表示xc、yc、zc,以及其原点位置Oc。当给定一个子坐标空间中的一点Ac=(a, b, c),我们同样可以依照上面4个步骤来确定其在父坐标空间下的位置Ap:
 模型空间
模型空间
模型空间(model space),如它的名字所暗示的那样,是和某个模型或者说是对象有关的。有时模型空间也被称为对象空间(object space)或局部空间(local space)。每个模型都有自己独立的坐标空间,当它移动或旋转的时候,模型空间也会跟着它移动和旋转。把我们自己当成游戏中的模型的话,当我们在办公室里移动时,我们的模型空间也在跟着移动,当我们转身时,我们本身的前后左右方向也在跟着改变。
在模型空间中,我们经常使用一些方向概念,例如“前(forward)”“后(back)”“左(left)”“右(right)”“上(up)”“下(down)”。在本书中,我们把这些方向称为自然方向。模型空间中的坐标轴通常会使用这些自然方向。在4.2.4节中我们讲过,Unity在模型空间中使用的是左手坐标系,因此在模型空间中,+x轴、+y轴、+z轴分别对应的是模型的右、上和前向。需要注意的是,模型坐标空间中的x轴、y轴、z轴和自然方向的对应不一定是上述这种关系,但由于Unity使用的是这样的约定,因此本书将使用这种方式。我们可以在Hierarchy视图中单击任意对象就可以看见它们对应的模型空间的3个坐标轴。
模型空间的原点和坐标轴通常是由美术人员在建模软件里确定好的。当导入到Unity中后,我们可以在顶点着色器中访问到模型的顶点信息,其中包含了每个顶点的坐标。这些坐标都是相对于模型空间中的原点(通常位于模型的重心)定义的。
世界空间
世界空间(world space)是一个特殊的坐标系,因为它建立了我们所关心的最大的空间。一些读者可能会指出,空间可以是无限大的,怎么会有“最大”这一说呢?这里说的最大指的是一个宏观的概念,也就是说它是我们所关心的最外层的坐标空间。以我们的农场游戏为例,在这个游戏里世界空间指的就是农场,我们不关心这个农场是在什么地方,在这个虚拟的游戏世界里,农场就是最大的空间概念。世界空间可以被用于描述绝对位置(较真的读者可能会再一次提醒我,没有绝对的位置。没错,但我相信读者可以明白这里绝对的意思)。在本书中,绝对位置指的就是在世界坐标系中的位置。通常,我们会把世界空间的原点放置在游戏空间的中心。
观察空间
观察空间(view space)也被称为摄像机空间(camera space)。观察空间可以认为是模型空间的一个特例——在所有的模型中有一个非常特殊的模型,即摄像机(虽然通常来说摄像机本身是不可见的),它的模型空间值得我们单独拿出来讨论,也就是观察空间。
摄像机决定了我们渲染游戏所使用的视角。在观察空间中,摄像机位于原点,同样,其坐标轴的选择可以是任意的,但由于本书讨论的是以Unity为主,而Unity中观察空间的坐标轴选择是:+x轴指向右方,+y轴指向上方,而+z轴指向的是摄像机的后方。读者在这里可能觉得很奇怪,我们之前讨论的模型空间和世界空间中+z轴指的都是物体的前方,为什么这里不一样了呢?这是因为,Unity在模型空间和世界空间中选用的都是左手坐标系,而在观察空间中使用的是右手坐标系。这是符合OpenGL传统的,在这样的观察空间中,摄像机的正前方指向的是-z轴方向。这种左右手坐标系之间的改变很少会对我们在Unity中的编程产生影响,因为Unity为我们做了很多渲染的底层工作,包括很多坐标空间的转换。但是,如果读者需要调用类似Camera.camera ToWorldMatrix、Camera.worldToCameraMatrix等接口自行计算某模型在观察空间中的位置,就要小心这样的差异。
最后要提醒读者的一点是,观察空间和屏幕空间(详见4.6.8节)是不同的。观察空间是一个三维空间,而屏幕空间是一个二维空间。从观察空间到屏幕空间的转换需要经过一个操作,那就是投影(projection)
顶点变换的第二步,就是将顶点坐标从世界空间变换到观察空间中。这个变换通常叫做观察变换(view transform)。
为了得到顶点在观察空间中的位置,我们可以有两种方法。一种方法是计算观察空间的3个坐标轴在世界空间下的表示,
这里我们使用第二种方法。由Transform组件可以知道,摄像机在世界空间中的变换是先按(30, 0, 0)进行旋转,然后按(0, 10, -10)进行了平移
裁剪空间
顶点接下来要从观察空间转换到裁剪空间(clip space,也被称为齐次裁剪空间)中,这个用于变换的矩阵叫做裁剪矩阵(clip matrix),也被称为投影矩阵(projection matrix)。裁剪空间的目标是能够方便地对渲染图元进行裁剪:完全位于这块空间内部的图元将会被保留,完全位于这块空间外部的图元将会被剔除,而与这块空间边界相交的图元就会被裁剪。那么,这块空间是如何决定的呢?答案是由视锥体(view frustum)来决定。
投影矩阵有两个目的。
·首先是为投影做准备。这是个迷惑点,虽然投影矩阵的名称包含了投影二字,但是它并没有进行真正的投影工作,而是在为投影做准备。真正的投影发生在后面的齐次除法(homogeneous division)过程中。而经过投影矩阵的变换后,顶点的w分量将会具有特殊的意义。
·其次是对x、y、z分量进行缩放。我们上面讲过直接使用视锥体的6个裁剪平面来进行裁剪会比较麻烦。而经过投影矩阵的缩放后,我们可以直接使用w分量作为一个范围值,如果x、y、z分量都位于这个范围内,就说明该顶点位于裁剪空间内。
6,法线变换
法线(normal),也被称为法矢量(normal vector)。在上面我们已经看到如何使用变换矩阵来变换一个顶点或一个方向矢量,但法线是需要我们特殊处理的一种方向矢量。在游戏中,模型的一个顶点往往会携带额外的信息,而顶点法线就是其中一种信息。当我们变换一个模型的时候,不仅需要变换它的顶点,还需要变换顶点法线,以便在后续处理(如片元着色器)中计算光照等。
一般来说,点和绝大部分方向矢量都可以使用同一个4×4或3×3的变换矩阵MA→B把其从坐标空间A变换到坐标空间B中。但在变换法线的时候,如果使用同一个变换矩阵,可能就无法确保维持法线的垂直性。下面就来了解一下为什么会出现这样的问题。
我们先来了解一下另一种方向矢量——切线(tangent),也被称为切矢量(tangent vector)。与法线类似,切线往往也是模型顶点携带的一种信息。它通常与纹理空间对齐,而且与法线方向垂直,
 顶点的切线和法线。切线和法线互相垂直
顶点的切线和法线。切线和法线互相垂直
由于切线是由两个顶点之间的差值计算得到的,因此我们可以直接使用用于变换顶点的变换矩阵来变换切线。假设,我们使用3×3的变换矩阵MA→B来变换顶点(注意,这里涉及的变换矩阵都是3×3的矩阵,不考虑平移变换。这是因为切线和法线都是方向矢量,不会受平移的影响),可以由下面的式子直接得到变换后的切线:TB=MA→BTA
其中TA和TB分别表示在坐标空间A下和坐标空间B下的切线方向。但如果直接使用MA→B来变换法线,得到的新的法线方向可能就不会与表面垂直了
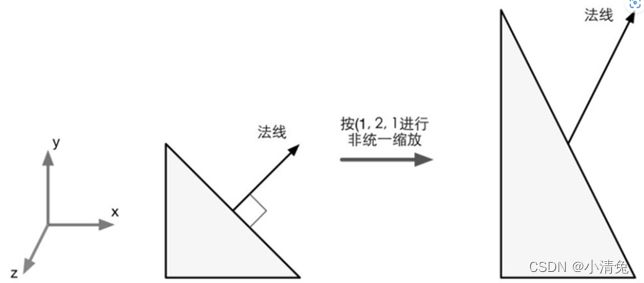
迚行非统一缩放时,如果使用和变换顶点相同的变换矩阵来变换法线,就会得到错误的结果,即变换后的法线方向与平面不再垂直
那么,应该使用哪个矩阵来变换法线呢?我们可以由数学约束条件来推出这个矩阵。我们知道同一个顶点的切线TA和法线NA必须满足垂直条件,即TA ·NA=0。给定变换矩阵MA→B,我们已经知道TB=MA→BTA。我们现在想要找到一个矩阵G来变换法线NA,使得变换后的法线仍然与切线垂直。即TB·NB=(MA→BTA)·(GNA)=0对上式进行一些推导后可得
![]()
由于TA· NA=0,因此如果 ,那么上式即可成立。也就是说,如果 ,即使用原变换矩阵的逆转置矩阵来变换法线就可以得到正确的结果。
值得注意的是,如果变换矩阵MA→B是正交矩阵,那么 ,因此[ ,也就是说我们可以使用用于变换顶点的变换矩阵来直接变换法线。如果变换只包括旋转变换,那么这个变换矩阵就是正交矩阵。而如果变换只包含旋转和统一缩放,而不包含非统一缩放,我们利用统一缩放系数k来得到变换矩阵MA→B的逆转置矩阵 。这样就可以避免计算逆矩阵的过程。如果变换中包含了非统一变换,那么我们就必须要求解逆矩阵来得到变换法线的矩阵。
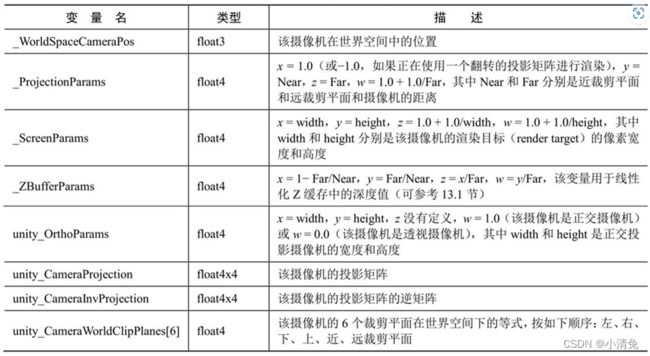
7,Unityshadwer的内置变量
1,变换矩阵
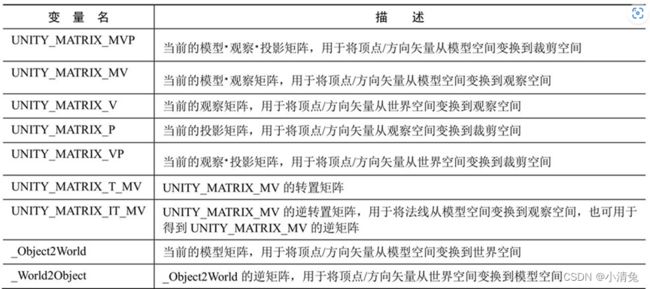
其中有一个矩阵比较特殊,即UNITY_MATRIX_T_MV矩阵。很多对数学不了解的读者不理解这个矩阵有什么用处。如果读者认真看过矩阵一节的知识,应该还会记得一种非常吸引人的矩阵类型——正交矩阵。对于正交矩阵来说,它的逆矩阵就是转置矩阵。因此,如果UNITY_MATRIX_MV是一个正交矩阵的话,那么UNITY_MATRIX_T_MV就是它的逆矩阵,也就是说,我们可以使用UNITY_MATRIX_T_MV把顶点和方向矢量从观察空间变换到模型空间。那么问题是,UNITY_MATRIX_MV什么时候是一个正交矩阵呢?读者可以从4.5节找到答案。总结一下,如果我们只考虑旋转、平移和缩放这3种变换的话,如果一个模型的变换只包括旋转,那么UNITY_MATRIX_MV就是一个正交矩阵。这个条件似乎有些苛刻,我们可以把条件再放宽一些,如果只包括旋转和统一缩放(假设缩放系数是k),那么UNITY_MATRIX_MV就几乎是一个正交矩阵了。为什么是几乎呢?因为统一缩放可能会导致每一行(或每一列)的矢量长度不为1,而是k,这不符合正交矩阵的特性,但我们可以通过除以这个统一缩放系数,来把它变成正交矩阵。在这种情况下,UNITY_MATRIX_MV的逆矩阵就是 而且,如果我们只是对方向矢量进行变换的话,条件可以放得更宽,即不用考虑有没有平移变换,因为平移对方向矢量没有影响。因此,我们可以截取UNITY_MATRIX_T_MV的前3行前3列来把方向矢量从观察空间变换到模型空间(前提是只存在旋转变换和统一缩放)。对于方向矢量,我们可以在使用前对它们进行归一化处理,来消除统一缩放的影响。
还有一个矩阵需要说明一下,那就是UNITY_MATRIX_IT_MV矩阵。我们在4.7节已经知道,法线的变换需要使用原变换矩阵的逆转置矩阵。因此UNITY_MATRIX_IT_MV可以把法线从模型空间变换到观察空间。但只要我们做一点手脚,它也可以用于直接得到UNITY_MATRIX_MV的逆矩阵——我们只需要对它进行转置就可以了。因此,为了把顶点或方向矢量从观察空间变换到模型空间,我们可以使用类似下面的代码:
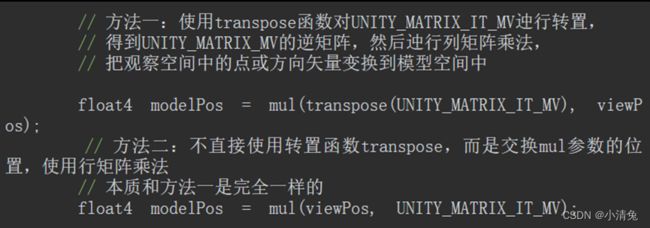
2,摄像机和屏幕参数
unity中的渲染优化
1,移动平台的特点
和PC平台相比,移动平台上的GPU架构有很大的不同。由于处理资源等条件的限制,移动设备上的GPU架构专注于尽可能使用更小的带宽和功能,也由此带来了许多和PC平台完全不同的现象。例如,为了尽可能移除那些隐藏的表面,减少overdraw(即一个像素被绘制多次), PowerVR芯片(通常用于iOS设备和某些Android设备)使用了基于瓦片的延迟渲染(Tiled-based Deferred Rendering, TBDR)架构,把所有的渲染图像装入一个个瓦片(tile)中,再由硬件找到可见的片元,而只有这些可见片元才会执行片元着色器。另一些基于瓦片的GPU架构,如Adreno(高通的芯片)和Mali(ARM的芯片)则会使用Early-Z或相似的技术进行一个低精度的的深度检测,来剔除那些不需要渲染的片元。还有一些GPU,如Tegra(英伟达的芯片),则使用了传统的架构设计,因此在这些设备上,overdraw更可能造成性能的瓶颈。
2,影响渲染的因素
首先,在学习如何优化之前,我们得了解影响游戏性能的因素有哪些,才能对症下药。对于一个游戏来说,它主要需要使用两种计算资源:CPU和GPU。它们会互相合作,来让我们的游戏可以在预期的帧率和分辨率下工作。其中,CPU主要负责保证帧率,GPU主要负责分辨率相关的一些处理。据此,我们可以把造成游戏性能瓶颈的主要原因分成以下几个方面。
(1)CPU。·
过多的draw call。
复杂的脚本或者物理模拟。
(2)(2)GPU。·顶点处理。
➢ 过多的顶点。
➢ 过多的逐顶点计算。
·片元处理。
➢ 过多的片元(既可能是由于分辨率造成的,也可能是由于overdraw造成的)。
➢ 过多的逐片元计算。
(3)带宽。
使用了尺寸很大且未压缩的纹理。
·分辨率过高的帧缓存。
(1)CPU优化。
·使用批处理技术减少draw call数目。
(2)GPU优化。
·减少需要处理的顶点数目。
➢ 优化几何体。
➢ 使用模型的LOD(Level of Detail)技术。
➢ 使用遮挡剔除(Occlusion Culling)技术。
·减少需要处理的片元数目
➢ 控制绘制顺序。
➢ 警惕透明物体。
➢ 减少实时光照。
·减少计算复杂度。
➢ 使用Shader的LOD(Level of Detail)技术。
➢ 代码方面的优化。
(3)节省内存带宽。·
减少纹理大小。
·利用分辨率缩放
3,Unity性能优化分析工具
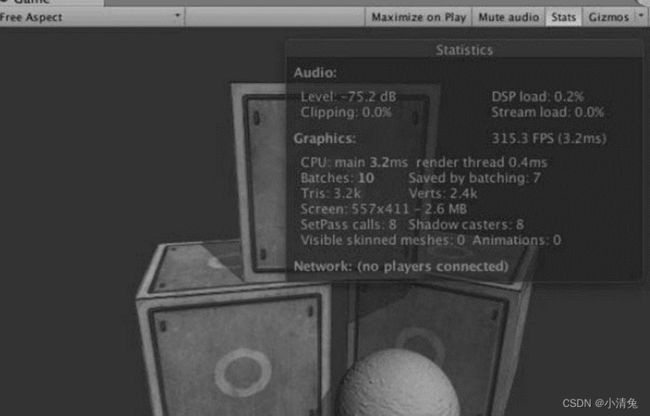

最明显的区别之一就是去掉了draw call数目的显示,而添加了批处理数目的显示。Batches和Saved by batching更容易让开发者理解批处理的优化结果。当然,如果我们想要查看draw call的数目等其他更加详细的数据,可以通过Unity编辑器的性能分析器来查看。
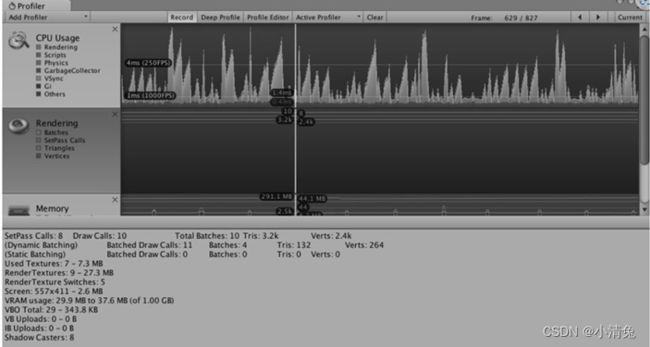
性能分析器显示了绝大部分在渲染统计窗口中提供的信息,例如,绿线显示了批处理数目、蓝线显示了Pass数目等,同时还给出了许多其他非常有用的信息,例如,draw call数目、动态批处理/静态批处理的数目、渲染纹理的数目和内存占用等
谈帧调试器
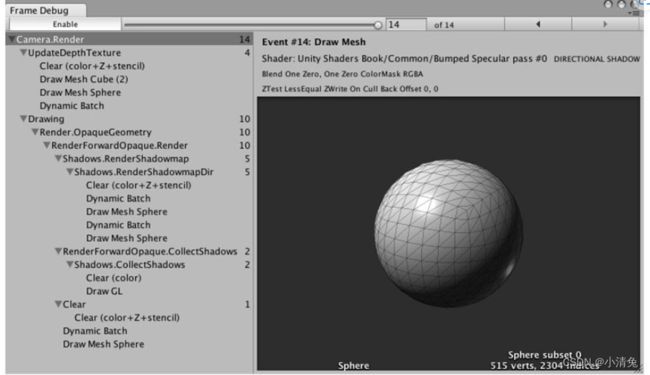
在Unity的渲染统计窗口、分析器和帧调试器这3个利器的帮助下,我们可以获得很多有用的优化信息。但是,很多诸如渲染时间这样的数据是基于当前的开发平台得到的,而非真机上的结果。事实上,Unity正在和硬件生产商合作,来首先让使用英伟达图睿(Tegra)的设备可以出现在Unity的性能分析器中。我们有理由相信,在后续的Unity版本中,直接在Unity中对移动设备进行性能分析不再是梦想。然而,在这个梦想实现之前,我们仍然需要一些外部的性能分析工具的帮助
4,减少drawcall
最常看到的优化技术大概就是批处理(batching)了。批处理的实现原理就是为了减少每一帧需要的draw call数目。为了把一个对象渲染到屏幕上,CPU需要检查哪些光源影响了该物体,绑定shader并设置它的参数,再把渲染命令发送给GPU。当场景中包含了大量对象时,这些操作就会非常耗时。一个极端的例子是,如果我们需要渲染一千个三角形,把它们按一千个单独的网格进行渲染所花费的时间要远远大于渲染一个包含了一千个三角形的网格。在这两种情况下,GPU的性能消耗其实并没有多大的区别,但CPU的draw call数目就会成为性能瓶颈。因此,批处理的思想很简单,就是在每次面对draw call时尽可能多地处理多个物体
Unity中支持两种批处理方式:一种是动态批处理,另一种是静态批处理。对于动态批处理来说,优点是一切处理都是Unity自动完成的,不需要我们自己做任何操作,而且物体是可以移动的,但缺点是,限制很多,可能一不小心就会破坏了这种机制,导致Unity无法动态批处理一些使用了相同材质的物体。而对于静态批处理来说,它的优点是自由度很高,限制很少;但缺点是可能会占用更多的内存,而且经过静态批处理后的所有物体都不可以再移动了(即便在脚本中尝试改变物体的位置也是无效的)
动态批处理
如果场景中有一些模型共享了同一个材质并满足一些条件,Unity就可以自动把它们进行批处理,从而只需要花费一个draw call就可以渲染所有的模型。动态批处理的基本原理是,每一帧把可以进行批处理的模型网格进行合并,再把合并后模型数据传递给GPU,然后使用同一个材质对其渲染。除了实现方便,动态批处理的另一个好处是,经过批处理的物体仍然可以移动,这是由于在处理每帧时Unity都会重新合并一次网格。
虽然Unity的动态批处理不需要我们进行任何额外工作,但只有满足条件的模型和材质才可以被动态批处理。需要注意的是,随着Unity版本的变化,这些条件也有一些改变。在本节中,我们给出一些主要的条件限制。
·能够进行动态批处理的网格的顶点属性规模要小于900。例如,如果shader中需要使用顶点位置、法线和纹理坐标这3个顶点属性,那么要想让模型能够被动态批处理,它的顶点数目不能超过300。需要注意的是,这个数字在未来有可能会发生变化,因此不要依赖这个数据。
·一般来说,所有对象都需要使用同一个缩放尺度(可以是(1, 1, 1)、(1, 2, 3)、(1.5, 1.4, 1.3)等,但必须都一样)。一个例外情况是,如果所有的物体都使用了不同的非统一缩放,那么它们也是可以被动态批处理的。但在Unity 5中,这种对模型缩放的限制已经不存在了。
·使用光照纹理(lightmap)的物体需要小心处理。这些物体需要额外的渲染参数,例如,在光照纹理上的索引、偏移量和缩放信息等。因此,为了让这些物体可以被动态批处理,我们需要保证它们指向光照纹理中的同一个位置。
·多Pass的shader会中断批处理。在前向渲染中,我们有时需要使用额外的Pass来为模型添加更多的光照效果,但这样一来模型就不会被动态批处理了
动态批处理的限制条件比较多,例如很多时候,我们的模型数据往往会超过900的顶点属性限制。这种时候依赖动态批处理来减少draw call显然已经不能够满足我们的需求了。这时,我们可以使用Unity的静态批处理技术。
静态批处理
Unity提供了另一种批处理方式,即静态批处理。相比于动态批处理来说,静态批处理适用于任何大小的几何模型。它的实现原理是,只在运行开始阶段,把需要进行静态批处理的模型合并到一个新的网格结构中,这意味着这些模型不可以在运行时刻被移动。但由于它只需要进行一次合并操作,因此,比动态批处理更加高效。静态批处理的另一个缺点在于,它往往需要占用更多的内存来存储合并后的几何结构。这是因为,如果在静态批处理前一些物体共享了相同的网格,那么在内存中每一个物体都会对应一个该网格的复制品,即一个网格会变成多个网格再发送给GPU。如果这类使用同一网格的对象很多,那么这就会成为一个性能瓶颈了。例如,如果在一个使用了1000个相同树模型的森林中使用静态批处理,那么,就会多使用1000倍的内存,这会造成严重的内存影响。这种时候,解决方法要么忍受这种牺牲内存换取性能的方法,要么不要使用静态批处理,而使用动态批处理技术(但要小心控制模型的顶点属性数目),或者自己编写批处理的方法
在内部实现上,Unity首先把这些静态物体变换到世界空间下,然后为它们构建一个更大的顶点和索引缓存。对于使用了同一材质的物体,Unity只需要调用一个draw call就可以绘制全部物体。而对于使用了不同材质的物体,静态批处理同样可以提升渲染性能。尽管这些物体仍然需要调用多个draw call,但静态批处理可以减少这些draw call之间的状态切换,而这些切换往往是费时的操作。从合并后的网格结构中我们还可以发现,尽管3个Teapot对象使用了同一个网格,但合并后却变成了3个独立网格。而且,我们可以从Unity的分析器中观察到在应用静态批处理前后VBO total的变化,从图16.10所示中可以看出,VBO(Vertex Buffer Object,顶点缓冲对象)的数目变大了。这正是因为静态批处理会占用更多内存的缘故,正如本节一开头所讲,静态批处理需要占用更多的内存来存储合并后的几何结构,如果一些物体共享了相同的网格,那么在内存中每一个物体都会对应一个该网格的复制品。
如果场景中包含了除了平行光以外的其他光源,并且在shader中定义了额外的Pass来处理它们,这些额外的Pass部分是不会被批处理的
处理平行光的Base Pass部分仍然会被静态批处理,因此,我们仍然可以节省两个draw call.
共享材质
从之前的内容可以看出,无论是动态批处理还是静态批处理,都要求模型之间需要共享同一个材质。但不同的模型之间总会需要有不同的渲染属性,例如,使用不同的纹理、颜色等。这时,我们需要一些策略来尽可能地合并材质。
如果两个材质之间只有使用的纹理不同,我们可以把这些纹理合并到一张更大的纹理中,这张更大的纹理被称为是一张图集(atlas)。一旦使用了同一张纹理,我们就可以使用同一个材质,再使用不同的采样坐标对纹理采样即可。
但有时,除了纹理不同外,不同的物体在材质上还有一些微小的参数变化,例如,颜色不同、某些浮点属性不同。但是,不管是动态批处理还是静态批处理,它们的前提都是要使用同一个材质。是同一个,而不是使用了同一种Shader的材质,也就是说它们指向的材质必须是同一个实体。这意味着,只要我们调整了参数,就会影响到所有使用这个材质的对象。那么想要微小的调整怎么办呢?一种常用的方法就是使用网格的顶点数据(最常见的就是顶点颜色数据)来存储这些参数。
前面说过,经过批处理后的物体会被处理成更大的VBO发送给GPU, VBO中的数据可以作为输入传递给顶点着色器,因此,我们可以巧妙地对VBO中的数据进行控制,从而达到不同效果的目的。一个例子是,森林场景中所有的树使用了同一种材质,我们希望它们可以通过批处理来减少draw call,但不同树的颜色可能不同。这时,我们可以利用网格的顶点的颜色数据来调整。
批处理的注意事项
在选择使用动态批处理还是静态批处理时,我们有一些小小的建设。
·尽可能选择静态批处理,但得时刻小心对内存的消耗,并且记住经过静态批处理的物体不可以再被移动。
·如果无法进行静态批处理,而要使用动态批处理的话,那么请小心上面提到的各种条件限制。例如,尽可能让这样的物体少并且尽可能让这些物体包含少量的顶点属性和顶点数目。
·对于游戏中的小道具,例如可以捡拾的金币等,可以使用动态批处理。·对于包含动画的这类物体,我们无法全部使用静态批处理,但其中如果有不动的部分,可以把这部分标识成“Static”。
除了上述提示外,在使用批处理时还有一些需要注意的地方。由于批处理需要把多个模型变换到世界空间下再合并它们,因此,如果shader中存在一些基于模型空间下的坐标的运算,那么往往会得到错误的结果。一个解决方法是,在shader中使用DisableBatching标签来强制使用该Shader的材质不会被批处理。另一个注意事项是,使用半透明材质的物体通常需要使用严格的从后往前的绘制顺序来保证透明混合的正确性。对于这些物体,Unity会首先保证它们的绘制顺序,再尝试对它们进行批处理。这意味着,当绘制顺序无法满足时,批处理无法在这些物体上被成功应用。
5,减少顶点片元数
减少顶点
尽管draw call是一个重要的性能指标,但顶点数目同样有可能成为GPU的性能瓶颈。我们将给出3个常用的顶点优化策略
优化几何体
在Unity的渲染统计窗口中,我们可以查看到渲染当前帧需要的三角面片数目和顶点数目。需要注意的是,Unity中显示的数目往往要多于建模软件里显示的顶点数,通常Unity中显示的数目要大很多。谁才是对的呢?其实,这是因为在不同的角度上计算的,都有各自的道理,但我们真正应该关心的是Unity里显示的数目
我们在这里简单解释一下造成这种不同的原因。三维软件更多地是站在我们人类的角度理解顶点的,即组成几何体的每一个点就是一个单独的点。而Unity是站在GPU的角度上去计算顶点数的。在GPU看来,有时需要把一个顶点拆分成两个或更多的顶点。这种将顶点一分为多的原因主要有两个:一个是为了分离纹理坐标(uv splits),另一个是为了产生平滑的边界(smoothing splits)。它们的本质,其实都是因为对于GPU来说,顶点的每一个属性和顶点之间必须是一对一的关系。而分离纹理坐标,是因为建模时一个顶点的纹理坐标有多个。例如,对于一个立方体,它的6个面之间虽然使用了一些相同的顶点,但在不同面上,同一个顶点的纹理坐标可能并不相同。对于GPU来说,这是不可理解的,因此,它必须把这个顶点拆分成多个具有不同纹理坐标的顶点。而平滑边界也是类似的,不同的是,此时一个顶点可能会对应多个法线信息或切线信息。这通常是因为我们要决定一个边是一条硬边(hard edge)还是一条平滑边(smooth edge)
对于GPU来说,它本质上只关心有多少个顶点。因此,尽可能减少顶点的数目其实才是我们真正需要关心的事情。因此,最后一条几何体优化建议就是:移除不必要的硬边以及纹理衔接,避免边界平滑和纹理分离。
模型的LOD技术
另一个减少顶点数目的方法是使用LOD(Level of Detail)技术。这种技术的原理是,当一个物体离摄像机很远时,模型上的很多细节是无法被察觉到的。因此,LOD允许当对象逐渐远离摄像机时,减少模型上的面片数量,从而提高性能。
在Unity中,我们可以使用LOD Group组件来为一个物体构建一个LOD。我们需要为同一个对象准备多个包含不同细节程序的模型,然后把它们赋给LOD Group组件中的不同等级,Unity就会自动判断当前位置上需要使用哪个等级的模型
遮挡剔除技术
我们最后要介绍的顶点优化策略就是遮挡剔除(Occlusion culling)技术。遮挡剔除可以用来消除那些在其他物件后面看不到的物件,这意味着资源不会浪费在计算那些看不到的顶点上,进而提升性能。我们需要把遮挡剔除和摄像机的视锥体剔除(Frustum Culling)区分开来。视锥体剔除只会剔除掉那些不在摄像机的视野范围内的对象,但不会判断视野中是否有物体被其他物体挡住。而遮挡剔除会使用一个虚拟的摄像机来遍历场景,从而构建一个潜在可见的对象集合的层级结构。在运行时刻,每个摄像机将会使用这个数据来识别哪些物体是可见的,而哪些被其他物体挡住不可见。使用遮挡剔除技术,不仅可以减少处理的顶点数目,还可以减少overdraw,提高游戏性能
模型的LOD技术和遮挡剔除技术可以同时减少CPU和GPU的负荷。CPU可以提交更少的draw call,而GPU需要处理的顶点和片元数目也减少了。
减少片元
另一个造成GPU瓶颈的是需要处理过多的片元。这部分优化的重点在于减少overdraw。简单来说,overdraw指的就是同一个像素被绘制了多次。Unity还提供了查看overdraw的视图,我们可以在Scene视图左上方的下拉菜单中选中Overdraw即可。实际上,这里的视图只是提供了查看物体相互遮挡的层数,并不是真正的最终屏幕绘制的overdraw。也就是说,可以理解为它显示的是,如果没有使用任何深度测试和其他优化策略时的overdraw。这种视图是通过把所有对象都渲染成一个透明的轮廓,通过查看透明颜色的累计程度,来判断物体之间的遮挡。当然,我们可以使用一些措施来防止这种最坏情况的出现
控制绘制顺序
时刻警惕透明物体
减少实时光照和阴影
6,节省带宽
大量使用未经压缩的纹理以及使用过大的分辨率都会造成由于带宽而引发的性能瓶颈
减少纹理大小
之前提到过,使用纹理图集可以帮助我们减少draw call的数目,而这些纹理的大小同样是一个需要考虑的问题。需要注意的是,所有纹理的长宽比最好是正方形,而且长宽值最好是2的整数幂。这是因为有很多优化策略只有在这种时候才可以发挥最大效用。在Unity 5中,即便我们导入的纹理长宽值并不是2的整数幂,Unity也会自动把长宽转换到离它最近的2的整数幂值。但我们仍然应该在制作美术资源时就把这条规则谨记在心,防止由于放缩而造成不好的影响。
除此之外,我们还应该尽可能使用多级渐远纹理技术(mipmapping)和纹理压缩。在Unity中,我们可以通过纹理导入面板来查看纹理的各个导入属性。通过把纹理类型设置为Advanced,就可以自定义许多选项,例如,是否生成多级渐远纹理(mipmaps),如图16.12所示。当勾选了Generate Mip Maps选项后,Unity就会为同一张纹理创建出很多不同大小的小纹理,构成一个纹理金字塔。而在游戏运行中就可以根据距离物体的远近,来动态选择使用哪一个纹理。这是因为,在距离物体很远的时候,就算我们使用了非常精细的纹理,但肉眼也是分辨不出来的。这种时候,我们完全可以使用更小、更模糊的纹理来代替,这可以让GPU使用分辨率更小的纹理,大量节省访问的像素数目。在某些设备上,关闭多级渐远纹理往往会造成严重的性能问题。因此,除非我们确定该纹理不会发生缩放,例如GUI和2D游戏中使用的纹理等,都应该为纹理生成相应的多级渐远纹理。
纹理压缩同样可以节省带宽。但对于像Android这样的平台,有很多不同架构的GPU,纹理压缩就变得有点复杂,因为不同的GPU架构有它自己的纹理压缩格式,例如,PowerVRAM的PVRTC格式、Tegra的DXT格式、Adreno的ATC格式。所幸的是,Unity可以根据不同的设备选择不同的压缩格式,而我们只需要把纹理压缩格式设置为自动压缩即可。但是,GUI类型的纹理同样是个例外,一些时候由于对画质的要求,我们不希望对这些纹理进行压缩
利用分辨率缩放
过高的屏幕分辨率也是造成性能下降的原因之一,尤其是对于很多低端手机,除了分辨率高其他硬件条件并不尽如人意,而这恰恰是游戏性能的两个瓶颈:过大的屏幕分辨率和糟糕的GPU。因此,我们可能需要对于特定机器进行分辨率的放缩。当然,这样可能会造成游戏效果的下降,但性能和画面之间永远是个需要权衡的话题。
7,减少计算复杂度
Shader的LOD技术
Shader的LOD技术可以控制使用的Shader等级。它的原理是,只有Shader的LOD值小于某个设定的值,这个Shader才会被使用,而使用了那些超过设定值的Shader的物体将不会被渲染
代码方面的优化
·尽可能不要使用分支语句和循环语句。
·尽可能避免使用类似sin、tan、pow、log等较为复杂的数学运算。我们可以使用查找表来作为替代。
·尽可能不要使用discard操作,因为这会影响硬件的某些优化。